convert 472 base 8 to base 5 and base 4
Answers
Answer:
I Think It's 12
Step-by-step explanation:
Please Tell Me If I'm Really wrong
Related Questions
Pete was building a doghouse for his dog, Chip. He made the door 36 inches tall. The height of the door was twice the height of the window in the doghouse.
Write an equation to determine the height of the window.
36 = 2h
36 = 2 + h
36 = h − 2
36 equals h over 2
Answers
Answer:
36 = 2h
Step-by-step explanation:
Here h represents the heigh
We know that the height of the door was twice the height of the window so that the equation will be
36 = 2h
Find the value of p when 3P = 1/9
Answers
Answer:
p=1/27
Step-by-step explanation:
3p=1/9
when 9 goes to the left land side divide changes into multiplication so 3p and 9 gets multiplied
3p*9=1
27p=1
when 27 goes the right hand side multiplication changes to division .So
p=1/27
The value of P is 1/27 for equation 3P = 1/9
What is Equation?Two or more expressions with an Equal sign is called as Equation.
Given,
Equation is 3P = 1/9
Three times of P equal to one by nine
We need to find the value of P
3P = 1/9
Divide both sides by nine
3P/3=1/9×1/3
P=1/27
Hence, the value of P is 1/27.
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ2
Find the length of the curve defined by from x=1 to x=9 y=2x
3/2
−9
Answers
To find the length of the curve defined by y =\(2x^(3/2)\) - 9, from x = 1 to x = 9, we use the arc length formula and integrate the square root of the sum of squares of the derivative of y with respect to x.
By evaluating this integral, we can determine the length of the curve.
To find the length of the curve defined by the equation y =\(2x^(3/2)\) - 9, from x = 1 to x = 9, we can use the arc length formula for a curve given by y = f(x) over the interval [a, b]:
L = ∫[a,b] √(1 + (f'\((x))^2\)) dx
First, we find the derivative of y with respect to x:
dy/dx = 3√(2x) / 2
Next, we substitute the derivative into the arc length formula and integrate over the interval [1, 9]:
L = ∫[1,9] √(1 + (3√(2x) / \(2)^2\)) dx
Simplifying the integrand, we have:
L = ∫[1,9] √(1 + 9x) dx
By evaluating this integral, we can determine the length of the curve.
To know more about arc length refer to-
https://brainly.com/question/31762064
#SPJ11
Someone help me pls

Answers
Answer:
360 miles
Step-by-step explanation:
45 miles=1 gallon
45x8=360
Answer:
360 miles
Step-by-step explanation:
8×45 ur just multiplying
Assuming that all years have 365 days and all birthdays occur with equal probability, how large must n be so that in any randomly chosen group of n people, the probability that two or more have the same birthday is at least 1/2?
Answers
it is seen that if the number of people in the group is n = 23, the probability that at least two people will have the same birthday is at least 1/2.
Let P(A) be the probability that in a randomly selected group of n people, at least two people have the same birthday.
If we assume that the year has 365 days, then the number of ways to select n people with different birthdays is n x (n-1) x (n-2) x ... x (n-364).
the probability of selecting n people with different birthdays is P(A') = n(n - 1)(n - 2)...(n - 364)/365nThen, the probability that at least two people in a group of n have the same birthday is given by P(A) = 1 - P(A').
We need to find the smallest value of n such that P(A) ≥ 1/2.Let's solve for this.Let us find n such that P(A) ≥ 1/2.
By using the complement rule, 1-P(A') = P(A).Then:1 - n(n - 1)(n - 2)...(n - 364)/365n ≥ 1/2n(n - 1)(n - 2)...(n - 364)/365n ≤ 1/2(2)n(n - 1)(n - 2)...(n - 364) ≤ 365n/2Now, take the natural logarithm of both sides and simplify as follows:ln[n(n - 1)(n - 2)...(n - 364)] ≤ ln[365n/2]nln(n) - ln[(n - 1)!] - ln[(n - 2)!] - ... - ln[2!] - ln[1!] ≤ ln[365n/2]
Therefore, we need at least 23 people in the group for the probability of two or more people having the same birthday to be at least 1/2.
This is because n = 23 is the smallest number for which the inequality holds, and therefore, it is the smallest number of people required to ensure that the probability of two or more people having the same birthday is at least 1/2.
To know more about number visit:
brainly.com/question/3589540
#SPJ11
Simplify the expression
-10(-9v+8)
Answers
Answer:
90v - 80
Step-by-step explanation:
-10 ( -9v + 8 )
Distributive property (multiply what is in the parenthesis by -10)
-10 * -9v + -10 * 8
90v - 80
2 negatives become a positive
Hope this helped!
Have a supercalifragilisticexpialidocious day!
Answer:90v-80
Step-by-step explanation:
Each morning Bill leaves home between 6:30 and 8:00 to drive to work at University of Texas. The time it takes Bill to drive to work (TIME) depends on the departure time when he leaves after 6:30 (DEPART), the number of red lights on the way (REDS) and the number of trains that he has to wait for at the crossing (TRAINS). Observations for these variables are for 231 working days in 2006. TIME is measured in minutes after 6:30 that Bill departs. The estimated regression model is as follows; TIME -19.9166+0.3692DEPART+1.3353REDS +2.7548TRAINS R¹ -0.634 s.e (1.2548) (0.3038) (0.01553) (0.1390) a) What is the average estimated time in minutes to drive to work for Bill when he leaves on time at 6:30 and there are no red lights and no trains at the crossroad to wait?
( b) Interpret the estimated coefficients of REDS and TRAINS. c) Using a 5% significance level, test the hypothesis that each train delays Bill by 3 minutes. State your conclusion.
Answers
a) The average estimated time for Bill to drive to work when he leaves on time at 6:30 with no red lights and no trains to wait for is approximately -19.9166 minutes. b) The estimated coefficients of REDS and TRAINS in the regression model are 1.3353 (REDS). c) The absolute value of the calculated t-value (-1.7733) is less than the critical t-value (1.9719), we fail to reject the null hypothesis.
a) To find the average estimated time in minutes for Bill to drive to work when he leaves on time at 6:30 and there are no red lights and no trains at the crossroad to wait, we substitute the values into the regression model:
TIME = -19.9166 + 0.3692(DEPART) + 1.3353(REDS) + 2.7548(TRAINS)
Given:
DEPART = 0 (as he leaves on time at 6:30)
REDS = 0 (no red lights)
TRAINS = 0 (no trains to wait for)
Substituting these values:
TIME = -19.9166 + 0.3692(0) + 1.3353(0) + 2.7548(0)
= -19.9166
Therefore, the average estimated time for Bill to drive to work when he leaves on time at 6:30 with no red lights and no trains to wait for is approximately -19.9166 minutes. However, it's important to note that negative values in this context may not make practical sense, so we should interpret this as Bill arriving approximately 19.92 minutes early to work.
b) The estimated coefficients of REDS and TRAINS in the regression model are:
1.3353 (REDS)
2.7548 (TRAINS)
Interpreting the coefficients:
- The coefficient of REDS (1.3353) suggests that for each additional red light, the estimated time to drive to work increases by approximately 1.3353 minutes, holding all other factors constant.
- The coefficient of TRAINS (2.7548) suggests that for each additional train Bill has to wait for at the crossing, the estimated time to drive to work increases by approximately 2.7548 minutes, holding all other factors constant.
c) To test the hypothesis that each train delays Bill by 3 minutes, we can conduct a hypothesis test.
Null hypothesis (H0): The coefficient of TRAINS is equal to 3 minutes.
Alternative hypothesis (Ha): The coefficient of TRAINS is not equal to 3 minutes.
We can use the t-test to test this hypothesis. The t-value is calculated as:
t-value = (coefficient of TRAINS - hypothesized value) / standard error of coefficient of TRAINS
Given:
Coefficient of TRAINS = 2.7548
Hypothesized value = 3
Standard error of coefficient of TRAINS = 0.1390
t-value = (2.7548 - 3) / 0.1390
= -0.2465 / 0.1390
≈ -1.7733
Using a significance level of 5% (or alpha = 0.05) and looking up the critical value for a two-tailed test, the critical t-value for 230 degrees of freedom is approximately ±1.9719.
Since the absolute value of the calculated t-value (-1.7733) is less than the critical t-value (1.9719), we fail to reject the null hypothesis. This means that there is not enough evidence to conclude that each train delays Bill by 3 minutes.
To know more about hypothesis visit:
brainly.com/question/30404845
#SPJ4
In each of Problems 17 and 18, find the fundamental set of solutions specified by Theorem 3.2.5 for the given differential equation and initial point.
17.y′′+y′−2y=0,t0=0
Answers
The fundamental set of solutions for the given differential equation is {e^(-2t), e^t}.
To find the fundamental set of solutions for the differential equation y'' + y' - 2y = 0 with the initial point t₀ = 0, we can follow the steps outlined in Theorem 3.2.5.
Find the characteristic equation:
The characteristic equation is obtained by substituting y = e^(rt) into the differential equation, where r is a constant:
r² + r - 2 = 0
Solve the characteristic equation:
Factoring the equation, we have:
(r + 2)(r - 1) = 0
Setting each factor equal to zero and solving for r, we get:
r₁ = -2
r₂ = 1
Determine the fundamental set of solutions:
The fundamental set of solutions is given by:
y₁(t) = e^(r₁t)
y₂(t) = e^(r₂t)
Substituting the values of r₁ and r₂, we have:
y₁(t) = e^(-2t)
y₂(t) = e^t
Therefore, the fundamental set of solutions for the given differential equation is {e^(-2t), e^t}.
To learn more about Equation:
brainly.com/question/29657983
#SPJ11
ABC is an isosceles triangle, where AB=AC, BC=24cm and perimeter of triangle ABC=60cm. Then, Prove That: Angle BAC > Angle ABC
Answers
Let's assume that the measure of angle BAC is less than or equal to the measure of angle ABC.
Since AB = AC, then angles BAC and BCA are also equal. Let's denote the measure of angle BAC as x, then the measure of angle ABC and angle BCA is also x.
According to the triangle inequality theorem, the sum of any two sides of a triangle must be greater than the third side. In our case, we have:
AB + BC > AC
AB + 24 > AC
2AB + BC > 2AC
2AB + 24 > 2AC
2AB > 2AC - 24
AB > AC - 12
Since AB = AC, then AC - 12 < AB = AC, which means AC < AC + 12. This is a contradiction, and therefore our assumption that the measure of angle BAC is less than or equal to the measure of angle ABC is false.
Therefore, we can conclude that Angle BAC > Angle ABC.
Plot the frequency response and the impulse response of the LTI system having the output y = 2te-ul for the input x) = -(t).
Answers
Given an LTI system that has an output y = 2te^-ul for the input x(t) = -(t). Here, e^-ul is the decay constant and is a real positive constant. The impulse response of the system can be found by considering the impulse input x(t) = δ(t).
The output of the system with an impulse input is given by y(t) = h(t), where h(t) is the impulse response of the system.We have,x(t) = -(t)..........(1)Applying derivative on both sides of the above equation, we get,y(t) = 2te^-ul, Applying derivative on both sides of the above equation, we get,
Plot of frequency response and Impulse response of the system Hence, the plot of frequency response and the impulse response of the LTI system is shown in the figure below:, the frequency response is given by H(jω) = (2/(-jω + ul)^2) where ω is the angular frequency. The impulse response of the system is given by h(t) = (2/ul^2)t.e^-ul.
To know more about system visit:
https://brainly.com/question/19843453
#SPJ11
15 = 2x – 10 step and solution
Answers
Answer:
12.5 =x
Step-by-step explanation:
15 = 2x – 10
Add 10 to each side
15+10 = 2x – 10+10
25 = 2x
Divide by 2
25/2 = 2x/2
12.5 =x
Answer:
25/2
Step-by-step explanation:
2x-10=15
+10 +10
2x=25
divide both sides by 2 to get 25/2
find the value of x.
does anyone know how to do this?

Answers
Answer:
x=4
From the principles of isosceles triangles, two opposite sides are equal.
So,
4x+23=10x-1
solving the linear equation, we'd have x to be 4.
Answer:
x=4
Step-by-step explanation:
it is isosoles triangle so the value of x solve as follow
4x+23=10x-1
23+1=10x-4x
24=6x
x=4
Karen set up an investment account when she was 18 years old. She put $500 a month into the account for 12 years. This account paid an average annual rate of interest of 5.75% compounded quarterly. At the end of the 12 years, at age 30, Karen took all the money from this investment and put it into a different account that paid a fixed annual rate of 7% compounded annually as long as she did not withdraw any of the money. At what age would Karen have $1000000 in this second account? Complete the tables and circle the value that was calculated for each table. First Account 50. PV FV Periods Rate Payment PMT/yr CMP/yr Second Account PV FV Periods Rate Payment PMT/yr CMP/yr How old is Karen when she has a million dollars? (Round to the nearest year)
Answers
The answer is:Karen would have $1000000 in the second account when she is 23 years old.
In order to calculate at what age Karen would have $1000000 in the second account, we need to calculate the future value of her investment in the first account, and then use that as the present value for the second account.Let us complete the tables given:
First Account PV: $0 FV: $0 Periods: 144 Rate: 5.75% Payment: $500 PMT/yr: 12 CMP/yr: 4Second Account PV: $163474.72 FV: $1000000 Periods: 23 Rate: 7% Payment: $0 PMT/yr: 1 CMP/yr: 1.
In the first account, Karen invested $500 a month for 12 years.
The total number of periods would be 12*4 = 48 (since it is compounded quarterly). The rate of interest per quarter would be (5.75/4)% = 1.4375%.
The PMT/yr is 12 (since she is investing $500 every month). Using these values, we can calculate the future value of her investment in the first account.FV of first account = (500*12)*(((1+(0.014375))^48 - 1)/(0.014375)) = $162975.15
Rounding off to the nearest cent, the future value of her investment in the first account is $162975.15.
This value is then used as the present value for the second account, and we need to find out at what age Karen would have $1000000 in this account. The rate of interest is 7% compounded annually.
The payment is 0 since she does not make any further investments in this account. The number of periods can be found by trial and error using the formula for future value, or by using the NPER function in Excel or a financial calculator.
Plugging in the values into the formula for future value, we get:FV of second account = 162975.15*(1.07^N) = $1000000Solving for N, we get N = 22.93. Rounding off to the nearest year, Karen would have $1000000 in the second account when she is 23 years old.
Therefore, the main answer is:Karen would have $1000000 in the second account when she is 23 years old.
To know more about rate of interest visit:
brainly.com/question/28272078
#SPJ11
what fraction is eqivilant to 500%
Answers
Answer:
5/1
Step-by-step explanation:
Answer:
5/1
Step-by-step explanation:

Multiply the following numbers. 9(-2) =
Answers
Answer:
-18
Step-by-step explanation:
Every time you multiply a positive number to a negative number, it will always be negative.
9(-2) = 9 * -2 = -18
Best of Luck!
the first term of an AP is 2,and the last term is 59.if the sum of the first terms is 610,Find the common difference
Answers
Answer:
d = 3
Step-by-step explanation:
The sum to n terms of an AP is
\(S_{n}\) = \(\frac{n}{2}\) ( a + l)
where a is the first term and l the last term
Here a = 2, l = 59 and sum = 610 , then
\(\frac{n}{2}\) (2 + 59) = 610
\(\frac{n}{2}\) × 61 = 610 ( divide both sides by 61 )
\(\frac{n}{2}\) = 10 ( multiply both sides by 2 to clear the fraction )
n = 20
Then the sequence has 20 terms with a₂₀ = 59
The nth term of an AP is
\(a_{n}\) = a + (n - 1)d
where d is the common difference , then
2 + 19d = 59 ( subtract 2 from both sides )
19d = 57 ( divide both sides by 19 )
d = 3
Find the side length x

Answers
Step by step.
By using Pythagorean theory, a right triangle side lengths are a^2 + b ^2 = c ^2.
We know “c” the hypotenuse is 10 and “b” the leg is 8. We are looking for “a” or side length “x”
Fill in the known values.
a^2 + 8^2 = 10^2
a^2 + 64 = 100.
Subtract 64 from both sides to isolate “a”
a^2 +64 -64 = 100 -64
a^2 = 36
Now take the square root of both sides to solve for “a”
a = 6
Suppose a department contains 10 men and 15 women. a) How many ways are there to form a committee of 6 people from the department? Explain your answer. b) How many ways are there to form a committee of 6 people from the department, if the number of men in the committee is equal to the number of females in the committee? Explain your answer. c) How many ways are there to form a committee of 6 people from the department, if the number of men in the committee is less than the number of females in the committee? Explain your answer.
Answers
a) The number of ways to form a committee of 6 people from the department is 177,100.
b) The number of ways to form a committee of 6 people with an equal number of men and women is 54,600.
c) The number of ways to form a committee of 6 people with more women than men is 91,455.
a) To form a committee of 6 people from the department, we can choose 6 individuals from a total of 25 people (10 men + 15 women). The order in which the committee members are chosen does not matter, and we are not concerned with any specific positions within the committee. Therefore, we can use the concept of combinations.
The number of ways to choose 6 people from a group of 25 is given by the combination formula:
C(25, 6) = 25! / (6! * (25 - 6)!) = 25! / (6! * 19!) = 177,100
Therefore, there are 177,100 ways to form a committee of 6 people from the department.
b) In this case, we need to choose an equal number of men and women for the committee. We can select 3 men from the available 10 men and 3 women from the available 15 women. Again, the order of selection does not matter.
The number of ways to choose 3 men from 10 is given by the combination formula:
C(10, 3) = 10! / (3! * (10 - 3)!) = 10! / (3! * 7!) = 120
Similarly, the number of ways to choose 3 women from 15 is:
C(15, 3) = 15! / (3! * (15 - 3)!) = 15! / (3! * 12!) = 455
To find the total number of ways to form a committee with an equal number of men and women, we multiply these two combinations:
Total = C(10, 3) * C(15, 3) = 120 * 455 = 54,600
Therefore, there are 54,600 ways to form a committee of 6 people with an equal number of men and women.
c) In this case, we need to form a committee with more women than men. We can choose 1 or 2 men from the 10 available men and select the remaining 6 - (1 or 2) = 5 or 4 women from the 15 available women.
For 1 man and 5 women:
Number of ways to choose 1 man from 10: C(10, 1) = 10
Number of ways to choose 5 women from 15: C(15, 5) = 3,003
For 2 men and 4 women:
Number of ways to choose 2 men from 10: C(10, 2) = 45
Number of ways to choose 4 women from 15: C(15, 4) = 1,365
The total number of ways to form a committee with more women than men is the sum of these two cases:
Total = (Number of ways for 1 man and 5 women) + (Number of ways for 2 men and 4 women)
= 10 * 3,003 + 45 * 1,365
= 30,030 + 61,425
= 91,455
Therefore, there are 91,455 ways to form a committee of 6 people with more women than men.
To know more about number of ways, refer here:
https://brainly.com/question/30649502
#SPJ4
245 tickets in 5 days what is the unit rate
Answers
Answer:
245/5 = 49 tickets per day
Answer:
245 / 5 = 49 so
49 tickets per day
Solve inequality. Graph and check your solution. (IF NO SOLUTION, WRITE NO SOLUTION, if all real numbers, write all real numbers.5x - 7 < equal to -2 2/3b > -8 3w - 7 - w < 2w + 4
Answers
See solution below
Explanation:
a) 5x - 7 ≤ -2
collect like terms:
5x ≤ -2 + 7
5x ≤ 5
Divide through by 5:
x ≤ 1
From the graph above, the inequality has a solution.
b) 2/3b > -8
\(\frac{2}{3b}>-8\)Cross multiply:
2 > -8(3b)
2 > -24b
Divide through by -24:
Note: when we divide an inequality by a negative number, the inequality sign changes.
2/-24 < b
-1/ 12 < b
Hence, b > -1/12
Note: To make it easier to graph, I represented b with x
From the graph above, the inequality has a solution.
c) 3w - 7 - w < 2w + 4
2w - 7 < 2w + 4
collect like terms:
2w - 2w < 4 + 7
0 < 11
Note: To make it easier to graph, I represented b with x
From the graph, the solution is for all real numbers.



can anyone plz help?

Answers
Answer:
89.76 yd^2
Step-by-step explanation:
The area is given by
A = bh
A = 10.2 * 8.8
A =89.76 yd^2
Complete the statement. Round to the nearest hundredth if necessary.
64 lb kg
Answers
Answer: you are dummy
Step-by-step explanation:dummy
Please only correct answers only I need to past this
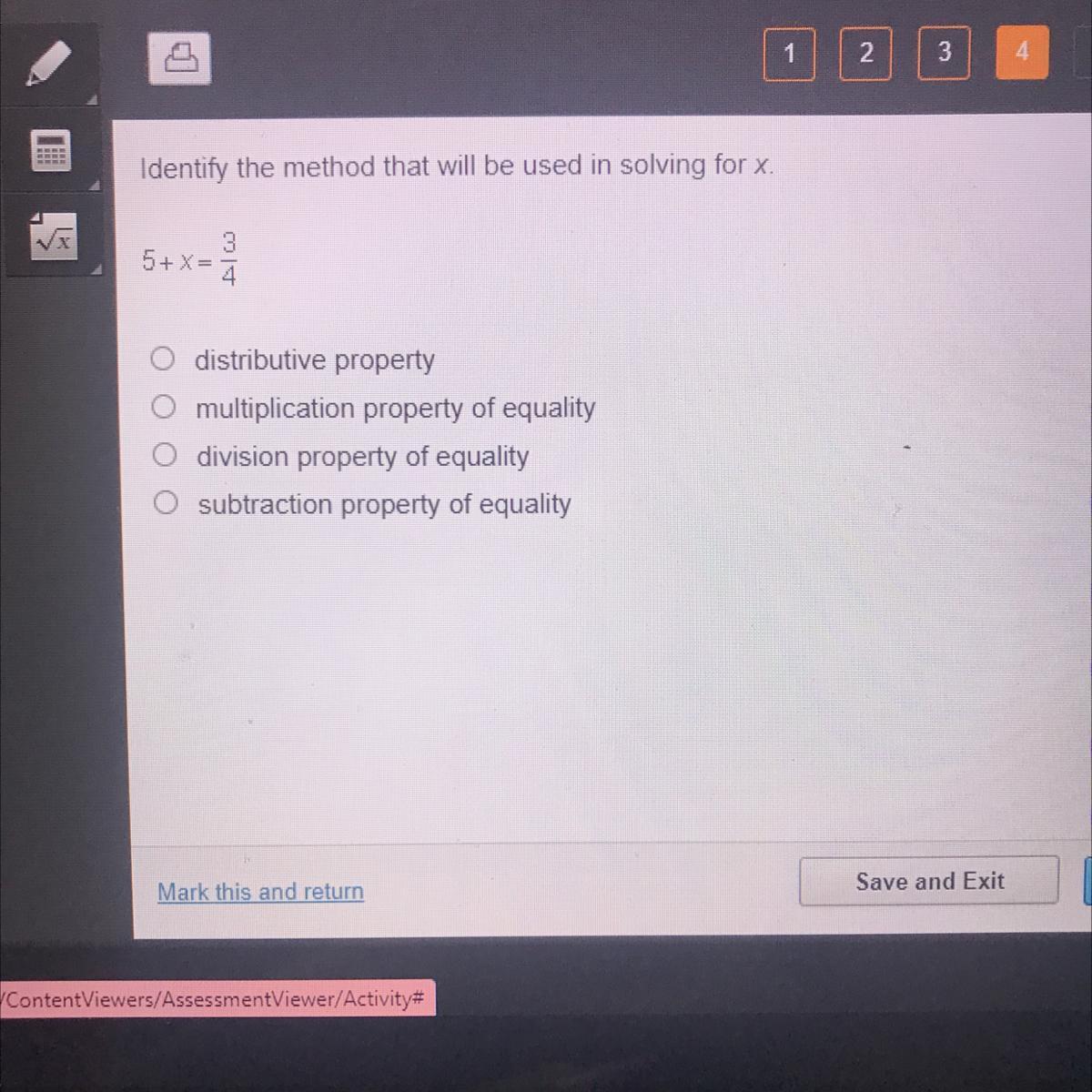
Answers
Answer:
Multiplication properly of equality
Emma says that Function A has a greater initial value. Is Emma correct? Justify your response.

Answers
Answer:
B. you can check the second one
For the science fair Carol wanted to see how many minutes of videos she watched were ads. She watched
6 videos with each video lasting 9 minutes. After watching the videos she calculated that she had watched 3 minutes of
ads over all the videos. How many minutes were not ads?
Answers
Answer:
51 mins were not ads
Step-by-step explanation:
1 video = 9 mins
6 videos = x
x = 9×6 = 54 mins
mins of ads = 3 mins
mins that were not ads = total mins of videos – total mins of ads
= 54 – 3 = 51 mins
if this helped pls give brainliest
Which of the following coordinates would be on the line y = 2x?
a) (0, 2)
b) (2, 0)
c) (1, 2)
d) (2, 2)
Answers
Answer:
The answer is C.
Step-by-step explanation:
You have to substitute the x-values into the equation to see whether it suits the y-value :
\(y = 2x\)
\(let \: x = 0 \\ y = 2(0) \\ y = 0 \: (incorrect)\)
\(let \: x = 2 \\ y = 2(2) \\ y = 4 \: (incorrect)\)
\(let \: x = 1 \\ y = 2(1) \\ y = 2 \: (correct)\)
\(let \: x = 2 \\ y = 2(2) \\ y = 4 \: (incorrect)\)
A pilot flies in a straight path for 1 h 30 min. She then makes a course correction, heading 10 degrees to the right of her original course, and flies 2 h in the new direction. If she maintains a constant speed of 670 mi/h, how far is she from her starting position?
Answers
On solving the provided question, we got to know that - distance she covered from her starting position is 2731 miles
What is equation?If two things are equal, an equation declares it. A "=" equals sign will appear in the format: 7 + 2 = 10 − 1 What is on the left (7 + 2) equals what is on the right (10 1), according to that equation. The statement "this equals that" is analogous to an equation.
The flight's first leg is 1020 miles long and lasts (1.5 hours) at 680 mph. We'll refer to this as our triangle's side B.
The second leg of the journey is 1360 miles (2 hours x 680 mph) long. We'll refer to this as the triangle's side C.
The law of cosines allows us to determine the triangle's side a's length.A is a 170° angle between the two sides whose lengths we are aware of. (180° - 10° = 170°).
\(a^2 = b^2 + c^2 - (2)*(a)*(b)*cos(A)\)
\(a^2 = (1020 miles)^2 + (1360 miles)^2 - (2)*(1020 miles)(1360 miles)*cos(170)\\ a^2 = 1040400 miles^2 + 1849600 miles^2 - (2774400 miles2)*cos(170)\\ cos(170) = -0.9848\\ a^2 = 2890000 miles^2 + 2732251 miles^2 = 5622250.6 miles^2\\ a = (5622250.6 miles^2)^{\frac{1}{2} } = 2371 miles\)
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
In the given figure , ∠BAC = 550 , ∠BCA = 620, the altitude BE produced meets the circle at D, determine ∠ACD, ∠DAC and ∠ADB.
Answers
The similarity statement that would be true for the given figure is;
A. ∆ DAB ~∆ DAC
What is similar triangles?Similar triangles are those triangles that have the same proportionate side lengths as well as related angle measurements.
here, we have,
Two triangles are said to be similar if their corresponding angles and sides have the same ratio. Similar triangles will possess the same form but may or may not have the same size.
The SAS similarity rule states that If the two sides of a triangle are in the same proportion of the two sides of another triangle, and the angle inscribed by the two sides in both the triangle are equal, then it means that the two triangles are similar.
The Side-Side-Side (SSS) similarity rule states that If all the three sides of a triangle are in proportion to the three sides of another triangle, then the two triangles are similar.
In this question, when we analyze the triangles well, it is clear that;
DA is congruent to itself by reflexive property of congruence.
Thus, we can say that ΔDAB is similar to ΔDAC,
Read more about Similar Triangles at;
brainly.com/question/14285697
#SPJ1
There are 20 boys and 18 girls in a class find the percentage of {1} boys {2} girls, in the class
Answers
Answer:
1. 52.63% 2. 47.36%
Step-by-step explanation:
20 + 18 = 38 total people
20 divided by 38 = 0.5263 to 52.63%
18 divided by 38 = 0.4736 to 47.36%
Hope this helps!
Tell whether the following is or is not a polygon and justify your answer

Answers
Answer: A. yes, closed and lines are straight B. No, curved lines C. no, curved lines D. yes, closed have lines are straight E. yes, closed have lines are straight E. yes, closed and lines are straight F. No, curved lines G. yes, closed and lines are straight H. yes, closed and lines are straight
Step-by-step explanation: