Convert 90.1% to a fraction in simplest form
Answers
The 90.1 percent can be written as a fraction in the simplest form is 901/1000.
What is percentage?It's the ratio of two integers stated as a fraction of a hundred parts. It is a metric for comparing two sets of data, and it is expressed as a percentage using the percent symbol.
We have a percentage 90.1%
To convert it into the fraction in the simplest form we can do as follows:
= 90.1%
\(= \dfrac{90.1}{100}\)
= 0.901
\(= \dfrac{901}{1000}\)
Thus, the 90.1 percent can be written as a fraction in the simplest form is 901/1000.
Learn more about the percentage here:
brainly.com/question/8011401
#SPJ1
Related Questions
find the degree of the monomial. 3x^8y^4
Answers
Answer:
Your answer is 12.
Step-by-step explanation:
Using log evaluate 3^x=10
Answers
Answer:
x ≈ 2.09590327429
Step-by-step explanation:
You want the solution to 3^x = 10 using logarithms.
LogsTaking logarithms of both sides of the given equation, we have ...
x·log(3) = log(10)
Dividing by the coefficient of x gives ...
x = log(10)/log(3)
x ≈ 2.09590327429
__
Additional comment
If the logarithm to the base 10 is used, then this becomes ...
x = 1/log₁₀(3)
The meaning of "log( )" varies with the context. In high-school algebra, it usually means "log₁₀( )". In other contexts, it may mean "ln( )", the natural logarithm.
For the purpose here, it doesn't matter what base the logarithms have, as long as log(10) and log(3) are to the same base.
<95141404393>

The approximate value of x that satisfies the equation 3^x = 10 is approximately 1.46497.
To evaluate the equation 3^x = 10 using logarithms, we can take the logarithm of both sides of the equation. The most commonly used logarithm is the base 10 logarithm, also known as the common logarithm (log).
Taking the log of both sides, we get:
log(3^x) = log(10)
Now, we can apply the logarithmic property that states log(a^b) = b * log(a). Applying this property to the left side of the equation:
x * log(3) = log(10)
Next, we can divide both sides of the equation by log(3) to isolate the variable x:
x = log(10) / log(3)
Using a calculator, we can evaluate the right side of the equation:
x ≈ 1.46497
Therefore, the approximate value of x that satisfies the equation 3^x = 10 is approximately 1.46497.
for such more question on equation
https://brainly.com/question/17482667
#SPJ8
Correct answer please

Answers
Answer:
50.75
Step-by-step explanation:
We have:
\(E[g(x)] = \int\limits^{\infty}_{-\infty} {g(x)f(x)} \, dx \\\\= \int\limits^{1}_{-\infty} {g(x)(0)} \, dx+\int\limits^{6}_{1} {g(x)\frac{2}{x} } \, dx+\int\limits^{\infty}_{6} {g(x)(0)} \, dx\\\\= \int\limits^{6}_{1} {g(x)\frac{2}{x} } \, dx\\\\=\int\limits^{6}_{1} {(4x+3)\frac{2}{x} } \, dx\\\\=\int\limits^{6}_{1} {(4x)\frac{2}{x} } \, dx + \int\limits^{6}_{1} {(3)\frac{2}{x} } \, dx\\\\=\int\limits^{6}_{1} {8} \, dx + \int\limits^{6}_{1} {\frac{6}{x} } \, dx\\\\\)
\(=8\int\limits^{6}_{1} \, dx + 6\int\limits^{6}_{1} {\frac{1}{x} } \, dx\\\\= 8[x]^{^6}_{_1} + 6 [ln(x)]^{^6}_{_1}\\\\= 8[6-1] + 6[ln(6) - ln(1)]\\\\= 8(5) + 6(ln(6))\\\\= 40 + 10.75\\\\= 50.74\)
A line goes through (-4,-5) and (2,-3). Write an equation that is perpendicular to the line above
Answers
9514 1404 393
Answer:
y = -3x
Step-by-step explanation:
The slope formula gives the slope of the segment between the given points.
m = (y2 -y1)/(x2 -x1)
m = (-3 -(-5))/(2 -(-4)) = 2/6 = 1/3
The slope of the perpendicular line is the opposite reciprocal of this, so is ...
m' = -1/(1/3) = -3
A perpendicular line is ...
y = -3x

Which property is illustrated by the following ?
if 2(x+y)= z, then 2x + 3y= z
Answers
In this case it’s the left side of the equation. In one situation you had 2(x+y) and in the other you had 2x+2y.
What property has you **distribute** the “2 times” outside the parentheses to each individual thing being added inside?
Use the ratio table to find the unit rate with respect to the specified units.
laps per minute
minutes /0/2/4/6/
laps / 0/1/2/3/
urgent!!!!! help bro!!!
Answers
The unit rate is given as follows:
0.5 laps per minute.
How to obtain the unit rate?The unit rate is obtained applying the proportions in the context of the problem.
The unit rate is desired in laps per minute, hence we must take a point, and divide the number of laps by the number of minutes.
In two minutes, one lap is completed, hence the unit rate is obtained as follows:
1/2 = 0.5 laps per minute.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
A well-known basketball coach has coached at the same university for 20 years. After what
seems like an infinite number of seasons, he finds that the mean number of points his teams score
is 72. One year he has an exceptionally tall team. The coach wants to know if the taller team
results in a greater number of points scored. Assume 72 to be the population mean with the
population variance unknown. The taller téam's scores are: '80, 88, 74, 82, 89, 90, 68, 95, 96, 72,
73 (it was a short season).
State the null and research hypotheses.
1) Report degrees of freedom (if applicable).:
2) Report the critical value using alpha= .05.:
3) Calculate the test statistics. :
4) In two or three sentences, briefly explain the results
(This includes your decision concerning the null hypothesis). :
Answers
Null hypothesis: The mean number of points scored by the taller team is not significantly different from the population mean of 72.
How did we determine the test statistic?Alternative hypothesis: The mean number of points scored by the taller team is significantly greater than the population mean of 72.
Since the population variance is unknown, we will use a t-test. The degrees of freedom for this test will be 9 (n-1), where n is the sample size of the taller team (10).
Using an alpha level of 0.05 and 9 degrees of freedom, the critical t-value is 1.833.
To calculate the test statistic, we first need to find the sample mean and standard deviation of the taller team's scores. The sample mean is 82, and the sample standard deviation is 9.89. Using these values, we can calculate the t-value:
t = (82-72) / (9.89 / sqrt(10)) = 3.19
Since the calculated t-value (3.19) is greater than the critical t-value (1.833), we reject the null hypothesis and conclude that there is a significant difference between the mean number of points scored by the taller team and the population mean of 72. The coach can therefore conclude that having a taller team does result in a greater number of points scored.
learn more more about Null hypothesis: https://brainly.com/question/13045159
#SPJ1
what number Could be added in the expression -4 -9 that the value of the expression is 0
Answers
sorry if this is confusing
Answer:
+13
Step-by-step explanation:
-4-9 gives -13
when +13 is added to -13 , the expression becomes +13+(-13) =13-13=0
An amount of Birr 500 is deposited in an account at the end of each six-month period with an interest computed at 6% compounded semi-annually. How many years does it take for the amount to reach Birr 56,398.43?
Answers
It would take approximately 17.12 years for the amount to reach Birr 56,398.43 with a deposit of Birr 500 at the end of each six-month period, compounded semi-annually at an interest rate of 6%.
To solve this problem, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A = Final amount
P = Principal amount (initial deposit)
r = Annual interest rate (in decimal form)
n = Number of compounding periods per year
t = Number of years
In this case, the principal amount is Birr 500, the annual interest rate is 6% (or 0.06), and the interest is compounded semi-annually, so there are 2 compounding periods per year.
We need to find the number of years (t) it takes for the amount to reach Birr 56,398.43.
Let's substitute the given values into the formula and solve for t:
56,398.43 = 500(1 + 0.06/2)^(2t)
Divide both sides by 500:
112.79686 = (1 + 0.03)^(2t)
Take the natural logarithm of both sides to eliminate the exponent:
ln(112.79686) = ln(1.03)^(2t)
Using the property of logarithms, we can bring down the exponent:
ln(112.79686) = 2t * ln(1.03)
Now, divide both sides by 2 * ln(1.03):
t = ln(112.79686) / (2 * ln(1.03))
Using a calculator, we find t ≈ 17.12.
For more such question on interest. visit :
https://brainly.com/question/25720319
#SPJ8
A student wants to reduce the size of an article he found in a newspaper. The original article was 12 cm wide. He needs to reduce it so its width measures 9 cm. On the copier, what percent setting should he can use to make a copy this size? PLEASE HURRYYYYY!!!!
Answers
It would be 25% decrease
You would put it in the formula of
old value - new value / old value x 100
So 12-9/12 x 100
which gives u 25 so it is 25%
Answer:
75%
Step-by-step explanation:
The scale factor the copier uses is the ratio of the copy size to the original size.
__
The student wants that ratio to be ...
copy size / original size = (9 cm)/(12 cm) = 9/12 = 3/4 = 75%
The student should use a setting of 75% to get the copy he wants.
Which of the following choices are binomial random variables?
Choose all answers that apply:
Choose all answers that apply:
(Choice A)
A
60\%60%60, percent of a certain species of tomato live after transplanting from pot to garden. Eli transplants 161616 of these tomato plants. Assume that the plants live independently of each other. Let T =T=T, equals the number of tomato plants that live.
(Choice B)
B
In a game of luck, a turn consists of a player continuing to roll a pair of six-sided dice until they roll a double (two of the same face values). Let X=X=X, equals the number of rolls in one turn.
(Choice C)
C
In a game involving a standard deck of 525252 playing cards, an individual randomly draws 777 cards without replacement. Let Y=Y=Y, equals the number of aces drawn.
Question came from Khan Acedamy
Answers
Answer:
A
Step-by-step explanation:
Answer: 60% of a certain species of tomato live after transplanting from pot to garden. Eli transplants 161616 of these tomato plants. Assume that the plants live independently of each other. Let T = the number of tomato plants that live.
Step-by-step explanation:
suppose that a linear system has five equations and three unknowns and that the rref of the coefficient matrix has a pivot in every column. then the linear system is consistent and has a unique solution.
Answers
Based on the information, then the linear system is not consistent and doesn't have a unique, therefore, it's false.
How to explain the informationIf the rref of the coefficient matrix has a pivot in every column, it means that the coefficient matrix has full column rank. However, this does not necessarily mean that the linear system is consistent and has a unique solution.
Since the linear system has more equations than unknowns, there may be redundant equations or inconsistencies among the equations. Therefore, the consistency of the linear system cannot be determined solely based on the rank of the coefficient matrix.
Therefore, the statement is false.
Learn more about equations on:
https://brainly.com/question/2972832
#SPJ1
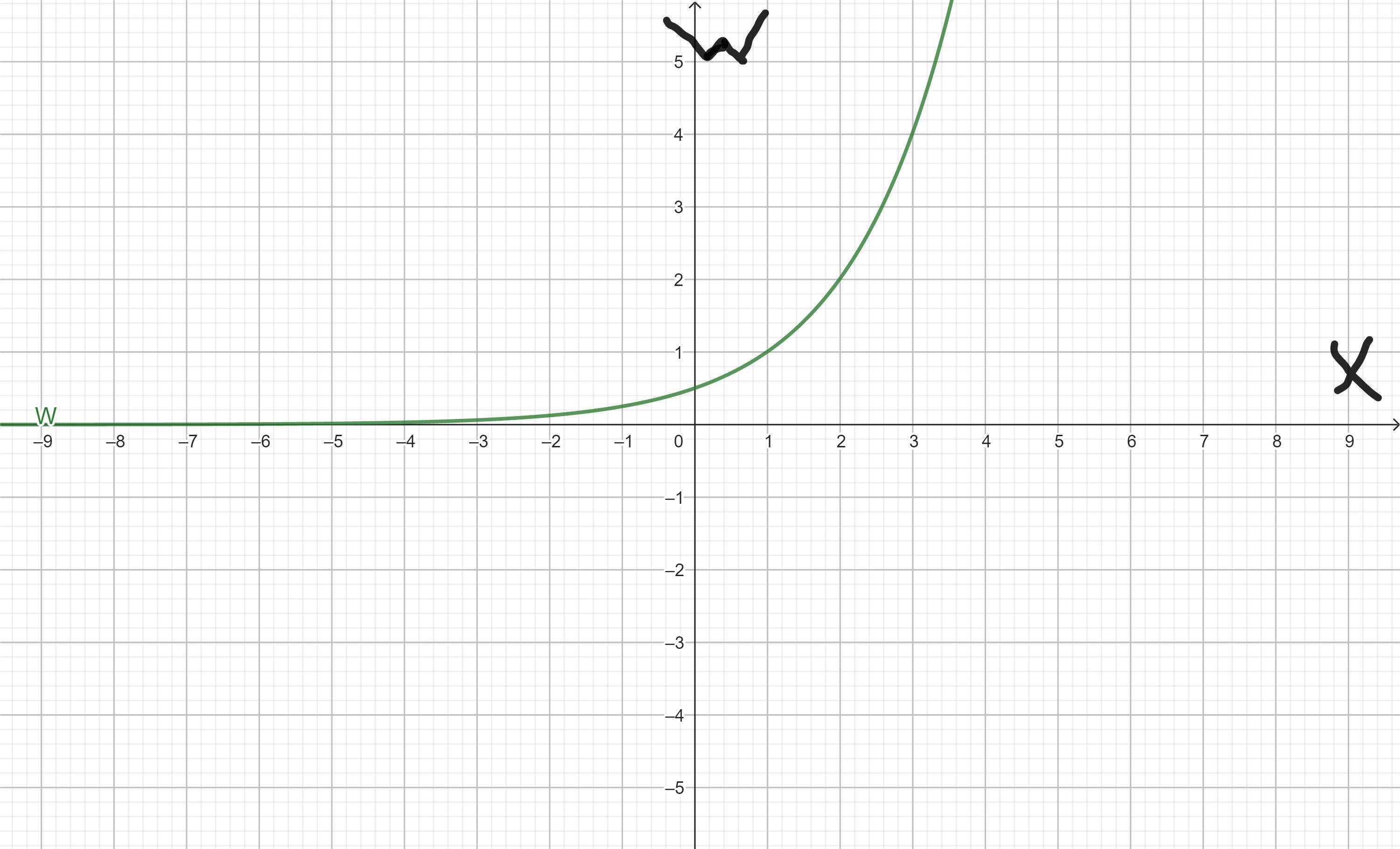
please help me with this i have 2o minutes to turn in please
here is the picture

Answers
The graph of the exponential function is on the image at the end.
How to graph the exponential equation?Here we have the exponential equation:
W(x) = 2^(x - 1)
To graph any function, we should find some points on the function, and to find, them, we need to evaluate the function in some values of x.
if x = 0
W(0) = 2^(0 -1 ) = 0.5
if x = 1
W(0) = 2^(1 - 1) = 2^0 = 1
if x = 2
W(0) = 2^(2 - 1) = 2^1 = 2
So we got the points (0, 0.5), (1, 1), and (2, 2) (you can try to find more points).
Now we need to graph them on the coordinate plane and draw a curve that connects them (with the general form of an exponential function).
The graph can be seen in the image below.
Learn more about exponential functions at:
https://brainly.com/question/2456547
#SPJ1
Estimate the product. 22×2.4 = _×_=_ Solve using an area model and the standard algorithm. Remember to express your products in standard form.
Answers
After putting the expression 4x² + x4 -8 -5 into Standard Form, what would be the leading
coefficient?
Answers
The leading coefficient of the expression is 1
How to determine the leading coefficient of the expressionFrom the question, we have the following parameters that can be used in our computation:
4x² + x4 -8 -5
When written in standard form, we have
x^4 + 4x^2 - 8 - 5
Evaluate the like terms
x^4 + 4x^2 - 13
The leading coeffiicient is the coefficient of the term with highest power
In this case, it is
Coefficient = 1
Hence, the value is 1
Read more about expression at
https://brainly.com/question/15775046
#SPJ1
write the expression as the sine or cosine of an angle
pi/5 cos pi/2+sin pi/2\cos pi/5
Answers
The given expression as a sine function is \(sin(\frac{\pi}{5} +\frac{\pi}{2} )\)
The addition formula for trigonometryThe given expression is:
\(sin(\frac{\pi}{5})cos(\frac{\pi}{2} ) + cos(\frac{\pi}{5})sin(\frac{\pi}{2} )\)
Note that:
\(sin(A+B)=sinAcosB+cosAsinB\)
Applying the addition principle to the given expression, we have:
\(sin(\frac{\pi}{5})cos(\frac{\pi}{2} ) + cos(\frac{\pi}{5})sin(\frac{\pi}{2} )=sin(\frac{\pi}{5} +\frac{\pi}{2} )\)
Therefore, the given expression as a sine function is \(sin(\frac{\pi}{5} +\frac{\pi}{2} )\)
Learn more on addition formula of trigonometry here: https://brainly.com/question/22852405
#SPJ1
At the beginning of a study, a certain culture of bacteria has a population of 340. The population grows according to a continuous exponential growth model. After 11 days, there are 544 bacteria.
(a) Lett be the time (in days) since the beginning of the study, and let y be the number of bacteria at time i. x 5 ? Write a formula relating y tot. Use exact expressions to fill in the missing parts of the formula. Do not use approximations.
y = 10:
(b) How many bacteria are there 23 days after the beginning of the study? Do not round any intermediate computations, and round your answer to the nearest whole number.
bacteria
Answers
Answer:
y = 340e^0.0427276t ; 908
Step-by-step explanation:
Given that :
t = time in days since study began
Number of bacteria after 11 days = 544
y = number of bacteria at time t
Exponential growth model:
y = ae^rt
Where a = initial amount ; r = Growth rate
y = 544 ; t = 11 ; a = 340
544 = 340*e^11t
544/340 = e^11t
1.6 = e^11t
Take the In of both sides
In(1.6) = 11t
0.4700036 = 11t
t = 0.4700036 / 11
t = 0.0427276
y = 340e^0.0427276t
Number of bacteria after 23 days :
Using the formula above :
t = 23
y = 340e^0.0427276(23)
y = 340 * 2.6717529
y = 908.39600
y = 908
The required formula is \(y = 340e^{0.0427}\)
908 bacteria are there 23 days after the beginning of the study .
Given that,
A certain culture of bacteria has a population of 340.
The population grows according to a continuous exponential growth model. After 11 days, there are 544 bacteria.
We have to find,
Write a formula relating y tot. Use exact expressions to fill in the missing parts of the formula.
How many bacteria are there 23 days after the beginning of the study.
According to the question,
Let t be the time (in days) since the beginning of the study,And let y be the number of bacteria at time,
t = time in days since study began
Number of bacteria after 11 days = 544
y = number of bacteria at time t
Then,
Exponential growth model:
\(y = a.e^{rt}\)
Where, a = initial amount ; r = Growth rate
y = 544 ; t = 11 ; a = 340
Then,
\(544 = 340.e^{11t}\\\\\dfrac{544}{340} = e^{11t}\\\\1.6 = e^{11t}\\\\Taking \ log \ on \ both \ sides,\\\\ln(1.6) = 11t\\\\0.47 = 11t \\\\t = \dfrac{0.47}{11}\\\\t = 0.0427\)
The required formula is \(y = 340e^{0.0427}\)
There 23 days after the beginning of the study Number of bacteria after 23 days :
\(y = 340e^{0.0427}\)
Where, t = 23
\(y = 340e^{0.0427276(23)}\\\\y = 340 \times 2.6717529\\\\y = 908.39600\\\\y = 908\)
Therefore, 908 bacteria are there 23 days after the beginning of the study .
To know more about Probability click the link given below.
https://brainly.com/question/21726505
1. In the figure, angle CAB is 47. What would prove that angle ACD is also 47?
A A reflection of ABC over AC, such that ABC maps to CDA.
B A rotation of ABC 180 clockwise around C, such that ABC maps to ADC.
C A rotation of ABC 180 counterclockwise around A, such that ABC maps to ADC.
D A translation of ABC to the top right, such that ABC maps to ADC.

Answers
The correct option C: A rotation of ABC 180 counterclockwise around A, such that ABC maps to ADC.
What is termed as the rotation?Geometry can be used to determine the meaning of rotation in mathematics. As a result, it is described as the movement of something around a center or an axis. Any rotation is regarded as a specific space motion that freezes at at least one point. In reality, a earth rotates on its axis, which is also an instance of rotation. Because a clockwise rotation has a negative magnitude, a counterclockwise rotation does have a positive magnitude.For the given question;
In triangles ABC angle CAB is 47.
If the triangles ABC and ACD becomes congruent such that angle ACD corresponds to angles ABC.
Then, both angles will be equal.
For, this, a rotation of ABC 180 counterclockwise around A, such that ABC maps to ADC is to be done.
To know more about the rotation, here
https://brainly.com/question/1164739
#SPJ13
What is equivalent to the expression below

Answers
Answer:
x^2+6x-15
Step-by-step explanation:
(3x^2+2x-8)-(2x^2-4x+7)
=3x^2+2x-8-2x^2+4x-7
=x^2+6x-15
Petra jogs 6 miles in 42 minutes. At this rate, how long would it take her to jog 8 miles?
Answers
Distance 1 / Time 1 = Distance 2 / Time 2
Using the information given:
6 miles / 42 minutes = 8 miles / Time 2
To solve for Time 2, we can cross-multiply and then divide:
6 miles * Time 2 = 8 miles * 42 minutes
6 * Time 2 = 8 * 42
6 * Time 2 = 336
Now, we divide both sides by 6 to isolate Time 2:
Time 2 = 336 / 6
Time 2 = 56 minutes
Therefore, it would take Petra 56 minutes to jog 8 miles at the same rate.
Answer:
56 minutes
Step-by-step explanation:
We can use proportions to solve.
6 miles 8 miles
------------ = ------------------
42 minutes x minutes
Using cross products.
6x = 42 *8
Divide each side by 6
x = 42/6 * 8
x = 7*8
x = 56
1. Which of the following identifies the a, b, c, and d of the absolute value function g(x) = −|2x| + 5?
Answers
The parameters of the absolute value function g(x) = -|2x| + 5 are given as follows:
a = -1.b = 2.c = 0.d = 5.How to obtain the parameters of the absolute value function?The standard definition of the absolute value function is given as follows:
f(x) = a|bx + c| + d.
The meaning of each parameter is given as follows:
a is the coefficient of vertical stretch/compression.b is the coefficient of horizontal stretch/compression.c is the coefficient of horizontal shift.d is the coefficient of vertical shift.In this problem, the function is defined as follows:
g(x) = −|2x| + 5.
Compared with the standard absolute value function, the values of these parameters are given as follows:
a = -1, b = 2, c = 0, d = 5.
More can be learned about the absolute value function at https://brainly.com/question/3381225
#SPJ1
Select the correct answer.
E
5
D
с
A
00
B
דן
F
-2.
2.
3
Which points define the solution set of this linear-quadratic system of equations?
A point A and point B
B. point D and point F
Cpoint C and point E
D. point B and point D

Answers
…………..
The distance around a rectangular cafe is 35m . The ratio of length of the cafe to the width is 3:2. Find the dimension of the cafe
Answers
Hi there! :)
Answer:
Length = 10.5 m, width = 7 m.
Step-by-step explanation:
Given:
Perimeter, or P = 35 m
Ratio of l to w = 3 : 2
Since the ratio is 3 : 2, let l = 3x, and w = 2x.
We know that the formula for the perimeter of a rectangle is P = 2l + 2w. Therefore:
35 = 2(3x) + 2(2x)
35 = 6x + 4x
35 = 10x
x = 3.5
Plug this value of "x" into each expression to solve for the dimensions:
2(3.5) = w
w = 7 m
3(3.5) = l
l = 10.5 m
Therefore, the dimensions are:
Length = 10.5 m, width = 7 m.
solve the following equation \(2x < 6\)
Answers
Answer:
x < 3
Step-by-step explanation:
Divide both sides of the inequality by 2
if a is parallel to b , then x is ?

Answers
From the given figure
If a // to b, then
The angle of measure (3x - 1) and the angle vertically opposite angle with 95 degrees are corresponding angles
Since corresponding angles are equal and the vertically opposite angles are equal, then
\(3x-1=95\)Add 1 to both sides
\(\begin{gathered} 3x-1+1=95+1 \\ 3x=96 \end{gathered}\)Divide both sides by 3 to find x
\(\begin{gathered} \frac{3x}{3}=\frac{96}{3} \\ x=\mathring{32} \end{gathered}\)The value of x is 32
Mohan is selling cookies at the economics fair. As he decides how to package the cookies, he finds that when he bags them in groups of 4, he has 3 left over. When he bags them in groups of 5, he has 2 left over. When he bags them in groups of 7, he has 4 left over. What is the least number of cookies that Mohan could have
Answers
Answer:
67 cookies
Step-by-step explanation:
When packaging in groups of 4, the possible number of cookies is x = (4n+3). The possible values are:
7, 11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, 55, 59, 63, 67, 71...
When packaging in groups of 5, the possible number of cookies is x = (5n+2). The possible values are:
7, 12, 17, 22, 27, 32, 37, 42, 47, 52, 57, 62, 67, 72, 77...
When packaging in groups of 7, the possible number of cookies is x = (7n+4). The possible values are:
11, 18, 25, 32, 39, 46, 53, 60, 67, 74, 81, 88, 95...
The least value that appears on all three possibilities is 67, therefore the least number of cookies that Mohan could have is 67.
The length of time it takes college students to ï¬nd a parking spot in the library parking lot follows a normal distribution with a mean of 5.5 minutes and a standard deviation of 1 minute. Find the probability that a randomly selected college student will take between 4.0 and 6.5 minutes to ï¬nd a parking spot in the library lot.
Answers
0.7745 is the probability that a randomly selected college student will take between 4.0 and 6.5 minutes to find a parking lot in the library lot.
What is probability?
The area of mathematics known as probability deals with numerical representations of the likelihood that an event will occur or that a statement is true. An event's probability is a number between 0 and 1, where, roughly speaking, 0 denotes the event's impossibility and 1 denotes certainty.
Here, we have
Given
Mean, μ = 5.5 minutes
Standard Deviation, σ = 1 minute
We are given that the distribution of length of time is a bell-shaped distribution that is a normal distribution.
z(score) = (x - μ)/σ
P(college student will take between 4.0 and 6.5 minutes)
= P(4.0 ≤ x ≤ 6.5)
= P((4.0 - 5.5)/1 ≤ z ≤ (6.5 - 5.5)/1)
= P(-1.5 ≤ z ≤ 1)
= P(z ≤ 1) - P(z < - 1.5)
= 0.8413 - 0.0668
= 0.7745 = 77.45%
Hence, 0.7745 is the probability that a randomly selected college student will take between 4.0 and 6.5 minutes to find a parking lot in the library lot.
To learn more about the probability from the given link
https://brainly.com/question/24756209
#SPJ4
does line n intersect line q?

Answers
Answer:
yes, line n intersects line q when the lines are extended
Step-by-step explanation:
the lines are not parallel, and any two nonparallel lines will always intersect at one point
Identify the sets that contain 2 as an element. (Check all that apply.)Check All That Apply{2, 3, 4, 5, ...}{2, 3, 4, 5, ...}{0, 1, 4, 9, ...}{0, 1, 4, 9, ...}{ 2, {2} }{ 2, {2} }{ {2}, { {2} } }{ {2}, { {2} } }{ {2}, { 2, {2} } }{ {2}, { 2, {2} } }{ { {2} } }{ { {2} } }
Answers
Question:
Identify the sets that contain 2 as an element. (Check all that apply.)
\(A.\ \{2, 3, 4, 5, ...\}\)
\(B.\ \{0, 1, 4, 9, ...\}\)
\(C.\ \{2, \{2\} \}\)
\(D.\ \{\{2\}, \{\{2\}\}\}\)
\(E.\ \{\{2\}, \{2, \{2\}\}\}\)
\(F.\ \{\{\{2\}\}\}\)
Answer:
\(A.\ \{2, 3, 4, 5, ...\}\)
\(C.\ \{2, \{2\} \}\)
Step-by-step explanation:
Required
For which of the options is 2 an element
\(A.\ \{2, 3, 4, 5, ...\}\)
The elements of this set starts from 2, then 3 and continues as thus.
Hence: 2 is an element
\(B.\ \{0, 1, 4, 9, ...\}\)
From the given elements in the above set, 2 is not listed.
Hence: 2 is not an element of this set
\(C.\ \{2, \{2\} \}\)
Here, 2 is listed as an element, 2 is also listed as a subset.
Since 2 is listed as an element, then 2 is an element of the set.
\(D.\ \{\{2\}, \{\{2\}\}\}\)
Here, 2 is listed as a subset of {2} and also as a subset of subset of {{2}}.
Since 2 is not listed as an element itself, then 2 is not an element of the set.
\(E.\ \{\{2\}, \{2, \{2\}\}\}\)
Here, 2 is listed as a subset of {2} and also as a subset of subset of {2,{2}}. This set only contains subsets, i.e. 2 is not listed as a direct element of the set.
Hence: 2 is not an element of the set
\(F.\ \{\{\{2\}\}\}\)
Here, 2 is listed as a subset of subset of {{2}}. This set only contains subsets, i.e. 2 is not listed as a direct element of the set.
Hence: 2 is not an element of the set
Answer:
how
Step-by-step explanation:
2=3√4x-12 x=? Please help with this question
Answers
Answer: 49/9
Step-by-step explanation:
\(2=3\sqrt{4x}-12\\\\14=3\sqrt{4x}\\\\\frac{14}{3}=\sqrt{4x}\\\\4x=\frac{196}{9}\\\\x=\frac{196}{36}\\\\x=\frac{49}{9}\)