Damian has two summer jobs. He works as a tutor, which pays $12 per hours, and he works as a lifeguard, which pays $9.50 per hour. He can work no more than 20 hours a week, but he wants to earn at least $220 per week. Which of the following systems of inequalities represents this situation, where x is the number of hours worked as a tutor, and y is the number of hours worked as a lifeguard? *
A 12x + 9.5y ≤ 220 AND x + y ≥ 20
B 12x + 9.5y ≤ 220 AND x + y ≤ 20
C 12x + 9.5y ≥ 220 AND x + y ≤ 20
D 12x + 9.5y ≥ 220 AND x + y ≥ 20
Answers
Answer:
answer b
Step-by-step explanation:
Related Questions
Jordan, Jessica, Eloise, and James travel to Europe. They see many famous places.
\
The friends hiked on a trail in the Austrian Alps. They hiked 1.08 kilometers on Monday and 0.94 kilometer on Tuesday.
How many kilometers did they hike in all? Describe how to use the grids to solve the problem. Then use the grids to find the solution.
Answers
The total number of kilometers that the friends hiked in all would be 2. 02 km.
How to solve for the total distance ?The total distance that Jordan, Jessica, Eloise, and James hiked in the Austrian Alps, can be found to be :
= Distance on Monday + Distance on Tuesday
= 1. 08 + 0. 94
= 2. 02 km
Using grids, you can represent a single box as 0. 1 km so that for 1. 08 km you will have a grid of 108 cubes. Do the same for Tuesday to get 94 cubes.
Add them up and you will get 202 cubes which would be 2.02 km.
Find out more on grids at https://brainly.com/question/25242892
#SPJ1
Find square of -9.2
Answers
Answer:
84.64.
Step-by-step explanation:
(-9.2)^2
= (9.2)^2
= 84.64.
What is the ratio of the number of pairs of Jeanine to the cost of jeans?

Answers
The Ratio of the number of pairs of Jeanine to the cost of jeans helps us understand how many pairs of jeans Jeanine can purchase for a given amount of money.
To find the ratio of the number of pairs of Jeanine to the cost of jeans, we need to first determine how many pairs of jeans Jeanine has and how much she paid for them. Let's assume Jeanine has 10 pairs of jeans and she paid $50 for each pair. Therefore, the total cost of Jeanine's jeans is $500.
Now we can calculate the ratio by dividing the number of pairs of jeans by the cost of jeans. So, the ratio of the number of pairs of Jeanine to the cost of jeans is:
10 pairs of jeans / $500 = 1/50
This means that for every $50 Jeanine spends on jeans, she gets one pair. Alternatively, we could also express the ratio as a decimal or percentage. In this case, the ratio as a decimal would be 0.02 or 2%, indicating that Jeanine spends 2% of the cost of one pair of jeans for each pair she owns.
Overall, the ratio of the number of pairs of Jeanine to the cost of jeans helps us understand how many pairs of jeans Jeanine can purchase for a given amount of money.
To Learn More About Ratio
https://brainly.com/question/12024093
SPJ11
Bookwork code: N84
Look at the poster below showing the price of pencils in a stationery shop.
Annabel wants to buy exactly 76 pencils. What is the lowest amount she can
pay?
Give your answer in pounds (£).
spar
..
Pencils for sale!
30p each
Pack of 10
pencils for £2
Answers
Based on mathematical operations, the lowest amount that Annabel can pay for pencils is $15.20
How is the lowest amount determined?The lowest amount that Annabel can pay for pencils can be determined using the mathematical operations of multiplication and division.
Multiplication and division are two of the four basic mathematical operations, including addition and subtraction.
If Annabel chooses to purchase the first pencil at 30p each, she would pay £22.80 (£0.30 x 76).
If Annabel chooses to purchase the second pencil class of a pack of 10 pencils for £2, she would pay £15.20 [£2 x (76 ÷ 10)].
Pencils for sale
30p each
Pack of 10 pencils for £2
Thus, if Annabel wants to buy the pencils, she can either pay £15.20 or £22.80, but using mathematical operations, the lowest amount she can pay is £15.20.
Learn more about mathematical operations at https://brainly.com/question/4721701.
#SPJ1
If a three-digit number is divided by 5 or by 6, remainder is 1 in each case. What is the least such three-digit number?
Answers
Answer:
The least three-digit number which leaves a remainder of 1 when divided by 5 or 6 is 101.
Step-by-step explanation:
This is because 101 is the smallest three-digit number which is not a multiple of either 5 or 6. To see that 101 is the smallest such number, you can check that 100 and 99 are both multiples of both 5 and 6, and 98 is a multiple of 6.
solve the following equation 5+7=11+7
Answers
Answer:
The equation, 5+7=11+7 solved step by step is:
5 plus 7, which equals 12.
And then, 11 plus 7, which equals 18.
You put it all together, it turns into 12=18 which isn't true.
So, your problem is not real.
Step-by-step explanation:
Your question has no answer because the two sides aren't equal.
Hope this helped! :)
Which side measures will not make a triangle

Answers
With a triangle, the sum of any two side lengths must be greater than the third side length. If this is not true, then the side lengths cannot make a triangle. Let's go through each set of side lengths and determine which would and wouldn't work.
a. 3, 4, 8 - will not make a triangle
3 + 4 = 7 > 8 = false
3 + 8 = 11 > 4 = true
4 + 8 = 12 > 3 = true
b. 7, 6, 12 - will make a triangle
7 + 6 = 13 > 12 = true
7 + 12 = 19 > 6 = true
6 + 12 = 18 > 7 = true
c. 5, 11, 13 - will make a triangle
5 + 11 = 16 > 13 = true
5 + 13 = 18 > 11 = true
11 + 13 = 24 > 5 = true
d. 4, 6, 12 - will not make a triangle
4 + 6 = 10 > 12 = false
4 + 12 = 16 > 6 = true
6 + 12 = 18 > 4 = true
e. 4, 6, 10 - will not make a triangle
4 + 6 = 10 > 10 = false
4 + 10 = 14 > 6 = true
6 + 10 = 16 > 4 = true
Hope this helps!
M/H
2. Last month, Sophie spent 39 hours watching TV and 36 hours playing
sport. During the same month, Fransina spent 42 hours watching TV and
36 hours playing sport. Who had the lower ratio of time spent watching
TV to time spent playing sport?
3. At a wedding, there were 40 people from the groom's side and 56 people
from the bride's side of the family.
a) Find the ratio of the groom's family to the bride's family at the
wedding.
b)
The cost of the catering for the wedding was R11 520. The bride and
groom decided to divide this cost using the ratio calculated in a).
How much did the groom and the bride each have to pay?
Answers
On solving the provided question, we can say that the equation that be formed is - 36x + 42y = 3 and the groom and the bride each have to pay 19.5 each
What is equation?A mathematical equation is a formula that joins two statements and uses the equal symbol (=) to indicate equality. A mathematical statement that establishes the equality of two mathematical expressions is known as an equation in algebra. For instance, in the equation 3x + 5 = 14, the equal sign places the variables 3x + 5 and 14 apart. The relationship between the two sentences on either side of a letter is described by a mathematical formula. Often, there is only one variable, which also serves as the symbol. for instance, 2x – 4 = 2.
the equation that be formed is -
36x + 42y = 3
the groom and the bride each have to pay 19.5 each
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
Daisy cream is sold in a bulk of 76 cups of cream. Kremlin cream is sold in a bulk of 4 1/2 gallons of cream. Marble cream is sold in a bulk of 40 pints of cream. Which one has the most cream?
Answers
Therefore , the solution of the given problem of unitary method comes out to be Daisy cream and Kremlin cream both have less cream per bulk 1 gallon and 4.5 gallons, respectively than Marble cream.
An unitary method is what?The objective can be accomplished by utilising what has already been discovered, taking advantage of this worldwide access, and including all essential components from earlier changeable study who employed a certain technique. If the anticipated claim outcome actually occurs, it will either be possible to contact the variable again or both important processes will undoubtedly miss the statement.
Here,
We must convert cups to gallons because daisy cream is sold in bulks of cups. Since a gallon of Daisy cream comprises 16 cups, one quantity of Daisy cream contains:
=> 16 cups per bulk = 1 gallon 16 cups per bulk = 1 gallon
Moscow cream is offered in bulk quantities of 4 1/2 gallons, which is one gallon.
Thus, we must convert pints to gallons. A gallon of Marble cream comprises eight pints, hence one quantity of Marble cream contains:
=> 40 pints in a bulk equal 1 gallon, 8 pints, or 5 gallons.
As a result, we can see that Marble cream, with 5 gallons per bulk, has the most cream.
Daisy cream and Kremlin cream both have less cream per bulk (1 gallon and 4.5 gallons, respectively) than Marble cream.
To know more about unitary method visit:
https://brainly.com/question/28276953
#SPJ1
A 78.0 kg sprinter starts a race with an acceleration of 1.64 m/s2. If the sprinter accelerates at that rate for 25 m, and then maintains that velocity for the remainder of the 100 m dash, what will be his time (in s) for the race?
Answers
The sprinter will complete the race in approximately 17.07 seconds.
To calculate the time for the race, we need to consider two parts: the acceleration phase and the constant velocity phase.
Acceleration Phase:
The acceleration of the sprinter is 1.64 m/s², and the distance covered during this phase is 25 m. We can use the equation of motion to calculate the time taken during acceleration:
v = u + at
Here:
v = final velocity (which is the velocity at the end of the acceleration phase)
u = initial velocity (which is 0 since the sprinter starts from rest)
a = acceleration
t = time
Rearranging the equation, we have:
t = (v - u) / a
Since the sprinter starts from rest, the initial velocity (u) is 0. Therefore:
t = v / a
Plugging in the values, we get:
t = 25 m / 1.64 m/s²
Constant Velocity Phase:
Once the sprinter reaches the end of the acceleration phase, the velocity remains constant. The remaining distance to be covered is 100 m - 25 m = 75 m. We can calculate the time taken during this phase using the formula:
t = d / v
Here:
d = distance
v = velocity
Plugging in the values, we get:
t = 75 m / (v)
Since the velocity remains constant, we can use the final velocity from the acceleration phase.
Now, let's calculate the time for each phase and sum them up to get the total race time:
Acceleration Phase:
t1 = 25 m / 1.64 m/s²
Constant Velocity Phase:
t2 = 75 m / v
Total race time:
Total time = t1 + t2
Let's calculate the values:
t1 = 25 m / 1.64 m/s² = 15.24 s (rounded to two decimal places)
Now, we need to calculate the final velocity (v) at the end of the acceleration phase. We can use the formula:
v = u + at
Here:
u = initial velocity (0 m/s)
a = acceleration (1.64 m/s²)
t = time (25 m)
Plugging in the values, we get:
v = 0 m/s + (1.64 m/s²)(25 m) = 41 m/s
Now, let's calculate the time for the constant velocity phase:
t2 = 75 m / 41 m/s ≈ 1.83 s (rounded to two decimal places)
Finally, let's calculate the total race time:
Total time = t1 + t2 = 15.24 s + 1.83 s ≈ 17.07 s (rounded to two decimal places)
Therefore, the sprinter will complete the race in approximately 17.07 seconds.
For such more questions on Sprinter Race Time Calculation
https://brainly.com/question/18963548
#SPJ8
A vehicle designed to operate on a drag strip accelerates from zero to 30m/s while undergoing a straight line path displacement of 45m. What is the vehicle's acceleration if its value may b assumed to be constant?
A.2.0m/s
B.5.0m/s
C.10m/s
D.15m/s
Answers
Answer:
C. 10 m/s²
Step-by-step explanation:
Given:
Δx = 45 m
v₀ = 0 m/s
v = 30 m/s
Find: a
v² = v₀² + 2aΔx
(30 m/s)² = (0 m/s)² + 2a (45 m)
a = 10 m/s²
The vehicle's acceleration if its value may b assumed to be constant is 10 m/s. Therefore, option C is the correct answer.
Given that, a vehicle designed to operate on a drag strip accelerates from zero to 30m/s while undergoing a straight line path displacement of 45m.
What is an acceleration?Acceleration is the name we give to any process where the velocity changes. Since velocity is a speed and a direction, there are only two ways for you to accelerate: change your speed or change your direction-or change both.
Here, Δx = 45 m, v₀ = 0 m/s and v = 30 m/s
Using the formula v² = v₀² + 2aΔx
(30 m/s)² = (0 m/s)² + 2b (45 m)
b = 10 m/s
The vehicle's acceleration if its value may b assumed to be constant is 10 m/s. Therefore, option C is the correct answer.
Learn more about the acceleration here:
https://brainly.com/question/12550364.
#SPJ2
factor 16n^4 -1 completely
Answers
Answer:
(4n^2 + 1) (2n+1) (2n-1)
Step-by-step explanation:
use difference of squares
if my answer is correct, pls mark this is brainliest! thanks!
Since both terms are perfect squares, factor using the difference of squares formula,
a² − b² = (a + b) (a − b) where a = 4n² and b=1.
(4n² + 1) (2n + 1) (2n − 1)
I dont know how to do this problem...

Answers
Answer:
Option B
Step-by-step explanation:
Refer the the picture for working

An elevator can carry up to 2500 pounds. Suppose the weight is 150 pounds. At most how many average-sized adults can safely ride the elevator at the same time? Write an inequality and solve. Let p represent the number of people who can safely ride the elevator.
Answers
Answer:
How much do the adukts weigh?
Step-by-step explanation:
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
help help help help

Answers
Answer:
2,341.779
Step-by-step explanation:
Solve: -1/2+ c =31/4 c=8 c=7 c=33/4 c=29/4
Answers
Answer:
c = 29/4Step-by-step explanation:
\( - \frac{1}{2} + c = \frac{31 }{4} \\ \\ c = \frac{31}{4} + \frac{1}{2} = \frac{31 - 2}{4} \\ \\ c = \frac{29}{4} \)
Hope this helps you
find f(2) PLEASE HELP SOLVE!! MATH!!!

Answers
The numeric value of the function f(x) = 14/[3 + ae^(kx)] at x = 2 is given as follows:
f(2) = 0.172.
How to obtain the numeric value of the function?The function for this problem is defined as follows:
f(x) = 14/[3 + ae^(kx)]
When x = 0, y = 2, hence we can obtain the coefficient a as follows:
2 = 14/(3 + a)
6 + a = 14
a = 8.
Hence:
f(x) = 14/[3 + 8e^(kx)]
When x = 1, y = 1/2, hence the coefficient k is given as follows:
0.5 = 14/(3 + 8e^k)
1.5 + 4e^k = 14
4e^k = 12.5
e^k = 12.5/4
k = ln(12.5/4)
k = 1.14.
Hence:
f(x) = 14/[3 + 8e^(1.14x)]
Then the numeric value of the function at x = 2 is given as follows:
f(2) = 14/[3 + 8e^(1.14(2))]
f(2) = 0.172.
Learn more about the numeric values of a function at brainly.com/question/28367050
#SPJ1
Given f(x)=x2+2x−8, find f(−2).
Question 2 options:
8
20
-8
-20

Answers
Answer:
-8 is the answers for the question
Step-by-step explanation:
please please give me brainlest
Allen has a piece of wood that is 10.5 feet long. He decides to cut it into 3 equal pieces to repair his deck. How long should he cut each piece?
Answers
Answer:
3.5 feet
I think is right
Earth is approximately 9.3 × 10^7 miles from the sun and Saturn is approximately 8.87 × 10^8 miles from the sun. Approximately how much further from the sun is Saturn than Earth?
PLZ ANSWER ASAP
Answers
Answer:
7.94 x 10⁸miles
Step-by-step explanation:
Given parameters:
Distance of earth from sun = 9.3 x 10⁷miles
Distance of earth from Saturn = 8.87 x 10⁸miles
Unknown:
How much further from the sun is Saturn than Earth = ?
Solution:
To find the solution to this problem, let us find the difference between their distances:
( 8.87 x 10⁸ miles - 9.3 x 10⁷ miles )
= 88.7 x 10⁷ miles - 9.3 x 10⁷ miles
= (88.7 - 9.3) x 10⁷miles
= 79.4 x 10⁷miles
= 7.94 x 10⁸miles
HELP PLZ IM GIVING 25 BRAIN:EIST PLZZZ
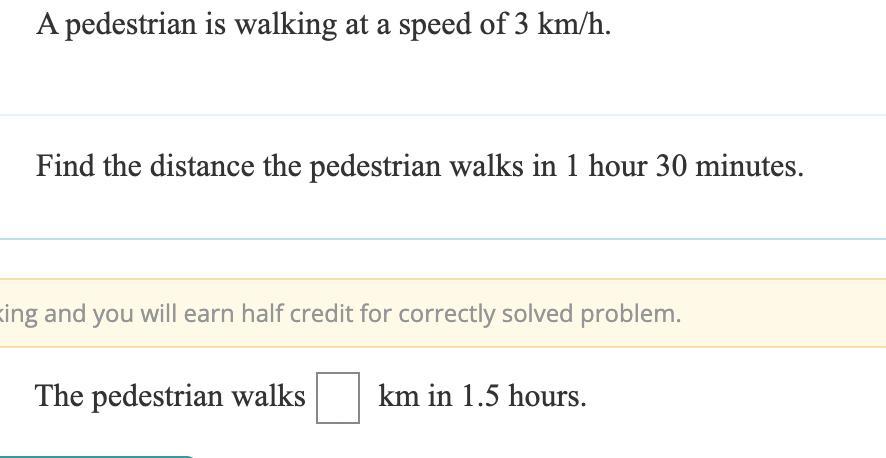
Answers
Answer:
2km
Step-by-step explanation:
Distance = Speed ÷ Time
Distance = 3 ÷ 1.5 (as 1 hour and 30 minutes is an hour and a half)
Distance = 2km
Answer:
4.5 km
Step-by-step explanation:
it takes an hour to walk 3. 1 hour is 60 minutes cut that in half to get 30, so you have to cut the 3 in half as well. which is 1.5. add 3 and 1.5 to get your answer 4.5
Use the following scenario to answer the question below:
You are deciding between two cars with different engines and want the bigger
of the two. One engine displaces 350 cubic inches. The other displaces 5,500
cubic centimeters. How many significant figures do the values in this problem
involve?
A. 4
B. 3
C. 2
D. 1

Answers
What is the axis of symmetry for this function?
y=x2 - 2x - 3
.
Answers
Answer:
x=1
Step-by-step explanation:
You can find the axis of symmetry from the equation of a function by using the formula x= -b / 2a ( ax^2 + bx + c).
In this particular function, you can see that b is 1 and c is -3.
x= -b / 2a
x= - (-2) / 2(1)
x= 2 / 1
x= 1
if f(x) = 3x +7 and g(x) = 2x - 5, find g[f(-3))]
a. -26
b. -9
c. -1
d. 10
Answers
Answer:
The value of g(f(-3) would be -9
Ella completed the following work to test the equivalence of two expressions.
What conclusion can you draw from Ella’s work?
Answers
Answer:D
Step-by-step explanation:
Two cards are drawn without replacement from a standard deck of 52 playing cards. What is the probability of choosing a spade for the second card drawn, if the first card, drawn without replacement, was a spade? Express your answer as a fraction or a decimal number rounded to four decimal places.
Answers
Answer:
12/51 or 0.2353
Step-by-step explanation:
There are 13 spades in a deck of 52 cards.
If the first card drawn is a spade and it is not replaced, we will have 51 cards, of which 12 are spades.
So the probability of drawing a spade for the second card is 12/51 ~ 0.2353
PLEASE HELP
how many solutions does this equation have? 12+2x-8=7x+5-5x
Answers
Answer:
no solution
Step-by-step explanation:
STEP 1: Since x is on the right side of the equation, switch the sides so it is on the left side of the equation.
\(7x+5-5x=12+2x-8\)
STEP 2: Subtract 5x from 7x.
\(2x+5=12+2x-8\)
STEP 3: Subtract 8 from 12.
\(2x+5=2x+4\)
STEP 4: Move all terms containing x to the left side of the equation.
\(5=4\)
STEP 5: Since 5≠4, there are no solutions.
No solution
Hii please answer i would appreciate it thankssss

Answers
Answer:
Just some background:
Congruent means that a triangle has the same angle measures and side lengths of another triangle.
SAS congruence theorem: If two sides and the angle between these two sides are congruent to the corresponding sides and angle of another triangle, then the two triangles are congruent. Congruent triangles: When two triangles have the same shape and size, they are congruent.
Let's look at A first.
The triangle on left, we know 40 and 30 degree angles. So 3 all angles together = 180, so the 3rd angle = 180-30-40 = 110.
Now look at the triangle on the right. The angle shown is 110! This angle is between the sides marked with || and ||| marks, indicating that those two sides are the same length between both triangles.
Therefore both triangles are the same by Side-Angle-Side or SAS.
Now look at B.
It's a right triangle. We are missing 1 side of each triangle.
Let's solve for the missing "leg" of the triangle on the right. The pythagorean theorem says that a^2 + b^2 = c^2 where a and b are the 'legs' or sides of the triangle and c is the hypotenuse (always the longest length opposite the right angle).
so 2^2 + b^2 = 4^2
4 + b^2 = 16
b^2 = 16-4
b^2 = 12
That missing side is the \(\sqrt{12}\).
This does NOT match the triangle on the left.
Theses two triangles are NOT congruent.
Hannah would like to make an investment that will turn 8000 dollars into 33000 dollars in 7 years. What quarterly rate of interest, compounded four times per year, must she receive to reach her goal?
Answers
Answer:
20.76%
Step-by-step explanation:
\(33000=8000(1+\frac{i}{4})^{4*7}\\4.125=(1+\frac{i}{4})^{28}\\\sqrt[28]{4.125}=1+\frac{i}{4} \\i= .207648169\)
which rounds to 20.76%
Answer:
About 0.2076 or 20.76%.
Step-by-step explanation:
Recall that compound interest is given by the formula:
\(\displaystyle A=P\left(1+\frac{r}{n}\right)^{nt}\)
Where A is the final amount, P is the principal, r is the interest rate, n is the number of times the interest is applied per year, and t is the number of years.
Since Hannah wants to turn an $8,000 investment into $33,000 in seven years compounded quarterly, we want to solve for r given that P = 8000, A = 33000, n = 4, and t = 7. Substitute:
\(\displaystyle \left(33000\right)=\left(8000\right)\left(1+\frac{r}{4}\right)^{(4)(7)}\)
Simplify and divide both sides by 8000:
\(\displaystyle \frac{33}{8}=\left(1+\frac{r}{4}\right)^{28}\)
Raise both sides to the 1/28th power:
\(\displaystyle \left(\frac{33}{8}\right)^{{}^{1}\! / \! {}_{28}}= 1+\frac{r}{4}\)
Solve for r. Hence:
\(\displaystyle r= 4\left(\left(\frac{33}{8}\right)^{{}^{1}\! / \! {}_{28}}-1\right)\)
Use a calculator. Hence:
\(r=0.2076...\approx 0.2076\)
So, the quarterly rate of interest must be 0.2076, or about 20.76%.