Determine the median, quartile 1, quartile 2 and the interquartile range for the following set
of data. Then, draw the box and whisker plot.
88 56 72 67 59 48 81 62 90 75 75 43 71 64 78 84
Answers
The median of the given set is 71, and the interquartile range is 22.
To find the median, arrange the data in ascending order: 43, 48, 56, 59, 62, 64, 67, 71, 72, 75, 75, 78, 81, 84, 88, 90. Since the number of data points is even, the median is the average of the middle two values, which in this case is 71.
Quartile 1 (Q1) is the median of the lower half of the data, which is the average of the middle two values in the first half: 56 and 59. So, Q1 = (56 + 59) / 2 = 57.5.
Quartile 3 (Q3) is the median of the upper half of the data, which is the average of the middle two values in the second half: 81 and 84. So, Q3 = (81 + 84) / 2 = 82.5.
The interquartile range (IQR) is the difference between Q3 and Q1: IQR = Q3 - Q1 = 82.5 - 57.5 = 25.
To draw the box and whisker plot, we start by drawing a number line and marking the minimum value (43) and the maximum value (90). Then, we draw a box from Q1 to Q3 (57.5 to 82.5) and a line inside the box to represent the median (71). Finally, we draw "whiskers" extending from the box to the minimum and maximum values.
To learn more about Interquartile range, visit:
https://brainly.com/question/31266794
#SPJ11
Related Questions
Evaluate the expression for x = 3, y = 1/3 , and z = 5.
12x − 3y / 4x − z
Answers
Step-by-step explanation:
Substitute the given values into the expression;
\(12(3) - 3( \frac{1}{3} ) \div 4(3) - 5\)
Multiply;
\(36 - 1 \div 12 - 5\)
Solve Using PEMDAS;
\(36 - \frac{1}{12} - 5\)
\(35 \frac{11}{12} - 5\)
\(\boxed{30 \frac{11}{12} } \)
[10 Points] .You deposit $750 each month into an account earning 7.9% interest compounded monthly. a) How much will you have in the account in 17 years? b) How much total money will you deposit into the account, after 17 years of making monthly deposits? c) How much total interest will you earn after 17 years?
Answers
a) After 17 years, you will have approximately $256,951.34 in the account. b) The total amount of money you will deposit into the account over 17 years is $153,000. c) The total interest you will earn after 17 years is approximately $103,951.34.
To calculate the future value of the account after 17 years, we can use the formula for compound interest:
FV = P *\((1 + r/n)^{(nt)\)
where : FV is the future value of the account
P is the monthly deposit amount ($750)
r is the annual interest rate (7.9% or 0.079)
n is the number of times the interest is compounded per year (monthly, so n = 12)
t is the number of years (17)
a) Plugging in the values, we have FV = 750 * (1 + 0.079/12)^(12*17) ≈ $256,951.34.
b) To calculate the total amount of money you will deposit into the account over 17 years, we multiply the monthly deposit amount by the number of months: Total deposits = 750 * 12 * 17 = $153,000.
c) The total interest earned can be calculated by subtracting the total deposits from the future value of the account: Total interest = FV - Total deposits = $256,951.34 - $153,000 ≈ $103,951.34.
Therefore, after 17 years, you will have approximately $256,951.34 in the account, the total deposits will amount to $153,000, and the total interest earned will be approximately $103,951.34.
learn more about total interest here:
https://brainly.com/question/14740098
#SPJ11
. Given A = 2î + 3ĵ + 4k and B = î - 2ĵ + 3k, find (a) A. B; (b) the acute angle between A and B; (c) the scalar component of A in the direction of B; and (d) AX B.
Answers
(a) The dot product of A and B is given by: A · B = (2î + 3ĵ + 4k) · (î - 2ĵ + 3k)= 2(1) + 3(-2) + 4(3)= 2 - 6 + 12 = 8
Therefore, A · B = 8.
(b) The angle between two vectors A and B is given by:
θ = cos^(-1)((A · B) / (|A| |B|))
In this case, |A| is the magnitude of vector A and |B| is the magnitude of vector B. The magnitude of a vector is given by the square root of the sum of the squares of its components.
|A| = √(2² + 3² + 4²) = √(4 + 9 + 16) = √29
|B| = √(1² + (-2)² + 3²) = √(1 + 4 + 9) = √14
Plugging in the values:
θ = cos^(-1)(8 / (√29 √14))
(c) The scalar component of vector A in the direction of vector B is given by:
A_B = (A · B) / |B|
Plugging in the values:
A_B = 8 / √14
(d) The cross product of vectors A and B is given by:
A x B = (2î + 3ĵ + 4k) x (î - 2ĵ + 3k)
= (3(3) - 4(-2))î + (4(1) - 2(3))ĵ + (2(-2) - 3(3))k
= 17î - 2ĵ - 13k
Therefore,AXB = 17î - 2ĵ - 13k.
Learn more about Dot Product here -: brainly.com/question/30404163
#SPJ11
(a) The dot product of A and B is given by: A · B = (2î + 3ĵ + 4k) · (î - 2ĵ + 3k)= 2(1) + 3(-2) + 4(3)= 2 - 6 + 12 = 8
Therefore, A · B = 8.
(b) The angle between two vectors A and B is given by:
θ = cos^(-1)((A · B) / (|A| |B|))
In this case, |A| is the magnitude of vector A and |B| is the magnitude of vector B. The magnitude of a vector is given by the square root of the sum of the squares of its components.
|A| = √(2² + 3² + 4²) = √(4 + 9 + 16) = √29
|B| = √(1² + (-2)² + 3²) = √(1 + 4 + 9) = √14
Plugging in the values:
θ = cos^(-1)(8 / (√29 √14))
(c) The scalar component of vector A in the direction of vector B is given by:
A_B = (A · B) / |B|
Plugging in the values:
A_B = 8 / √14
(d) The cross product of vectors A and B is given by:
A x B = (2î + 3ĵ + 4k) x (î - 2ĵ + 3k)
= (3(3) - 4(-2))î + (4(1) - 2(3))ĵ + (2(-2) - 3(3))k
= 17î - 2ĵ - 13k
Therefore,AXB = 17î - 2ĵ - 13k.
Learn more about Dot Product here -: brainly.com/question/30404163
#SPJ11
The average of a sample of high daily temperature in a desert is 114 degrees F, a sample standard deviation or 5 degrees F, and 26 days were sampled. What is the 90% confidence interval for the average temperature? Please state your answer in a complete sentence, using language relevant to this question.
Answers
In a sample of 26 days from the desert, the average of the high daily temperature is 114 degrees F, and the sample standard deviation is 5 degrees F.
To determine the 90% confidence interval for the average temperature, we can use the t-distribution as follows:To find the critical value of t, we can use the t-table. Since our sample has n = 26, the degrees of freedom (df) are n - 1 = 25. At a confidence level of 90%, with 25 degrees of freedom, the critical t-value is 1.708.The standard error of the mean is calculated as s / sqrt(n), where s is the sample standard deviation and n is the sample size. Therefore, the 90% confidence interval for the average temperature is (114 - 1.67, 114 + 1.67), or (112.33, 115.67) degrees F.
To know more about average visit :-
https://brainly.com/question/8501033
#SPJ11
Juwad picked 30 bags of apples on Monday and sold them at his fruit stand for
$3.45 each. The following week he picked and sold 26 bags.
How much money did Juwad earn in the first week?
How much money did he earn in the second week? How much did Juwad earn selling bags of apples these two weeks? Each bag Juwad picked holds 15 apples. How many apples did he pick in two
weeks?
Answers
Answer:
89.70 dollars
Step-by-step explanation:
If Juwad picked 30 bags of apples and only sold 26 of them for 3.45 each, then you would have to multiply the number of bags sold by the price, and you would get your answer. So in this case:
1. (#sold)* (price)= total amount of money made
2. 26*3.45= 89.70
3. And you can check by dividing 89.70(your answer) by the price of the apples
4. 89.70/3.45= 26
how does DIAMETER of wire affect:
Strength
range
stiffness
Answers
The diameter of a wire significantly impacts its strength, range, and stiffness.
1. Strength: As the diameter of a wire increases, its overall strength improves. A larger cross-sectional area allows the wire to withstand greater forces before breaking. This is because the increased material can distribute force more effectively, resulting in enhanced tensile strength.
2. Range: The diameter of a wire also influences its range or length. Thicker wires tend to have shorter range capabilities compared to thinner wires. As the diameter increases, the weight and stiffness of the wire rise as well, making it harder to extend or coil over long distances. Conversely, thinner wires are more flexible and lightweight, enabling them to cover greater lengths.
3. Stiffness: Lastly, the diameter of a wire impacts its stiffness, which is the resistance of the wire to bending or deformation. With a larger diameter, the stiffness of the wire increases due to the higher amount of material present. This means that it requires more force to bend or change the shape of the wire, resulting in greater rigidity. On the other hand, wires with smaller diameters are more pliable and can easily be bent or manipulated.
In summary, the diameter of a wire plays a crucial role in determining its strength, range, and stiffness. Thicker wires exhibit enhanced strength and stiffness but may have limited range capabilities, while thinner wires are more flexible and suitable for longer distances but may not be as strong or rigid.
To learn more about tensile strength : brainly.com/question/14368662
#SPJ11
AC is a diameter of OE, the area of
the
circle is 2897 units², and AB = 16 units.
Find BC and mBC.
B
A
C
E

Answers
Given that AC is a diameter of the circle, we can conclude that triangle ABC is a right triangle, with AC being the hypotenuse. The area of the circle is not directly related to finding the lengths of BC or AB, so we will focus on the given information: AB = 16 units.
Using the Pythagorean theorem, we can find BC. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (AC) is equal to the sum of the squares of the other two sides (AB and BC):
AC² = AB² + BC²
Substituting the given values, we have:
(AC)² = (AB)² + (BC)²
(AC)² = 16² + (BC)²
(AC)² = 256 + (BC)²
Now, we need to find the length of AC. Since AC is a diameter of the circle, the length of AC is equal to twice the radius of the circle.
AC = 2 * radius
To find the radius, we can use the formula for the area of a circle:
Area = π * radius²
Given that the area of the circle is 2897 units², we can solve for the radius:
2897 = π * radius²
radius² = 2897 / π
radius = √(2897 / π)
Now we have the length of AC, which is equal to twice the radius. We can substitute this value into the equation:
(2 * radius)² = 256 + (BC)²
4 * radius² = 256 + (BC)²
Substituting the value of radius, we have:
4 * (√(2897 / π))² = 256 + (BC)²
4 * (2897 / π) = 256 + (BC)²
Simplifying the equation gives:
(4 * 2897) / π = 256 + (BC)²
BC² = (4 * 2897) / π - 256
Now we can solve for BC by taking the square root of both sides:
BC = √((4 * 2897) / π - 256)
To find the measure of angle BC (mBC), we know that triangle ABC is a right triangle, so angle B will be 90 degrees.
In summary:
BC = √((4 * 2897) / π - 256)
mBC = 90 degrees
for similar questions on area of the circle.
https://brainly.com/question/14068861
#SPJ8
I need help, Find PG if GU=7.

Answers
Answer:
PG = 14 unit
Step-by-step explanation:
Given:
Equilateral triangle PQR.
GU = 7
Find:
PG
Computation:
We know that PQR is an equilateral triangle and PU is median.
Median of an equilateral triangle intersect each other at 2:1
So,
PG = 2 × GU
PG = 2 × 7
PG = 14 unit
Error in the Approximation < a < b < 100 Suppose you approximate P(a M100 b) by e Let a and b be two integers with 0 What is the largest possible error you could make?
Answers
The largest possible error you could make in approximating P(a < M < b) by e is when a = 0 and b = 1. The error would be |P(0 < M < 1) - e|.
You are given an approximation of P(a < M < b) by e, where M is an integer between a and b. You want to find the largest possible error in this approximation. The range of values for M is between a and b, and both a and b are integers between 0 and 100. The largest possible error would occur when the difference between the true value and the approximation is at its maximum. Since e is an approximation of P(a < M < b), the largest error would occur when the difference between the actual probability and the approximation is at its maximum.
This would happen when the actual probability is either very close to 0 or 1, and the approximation is far from the actual value. Since a and b are integers between 0 and 100, the largest possible error would occur when the range of possible values for M is at its smallest. This means that a and b should be as close together as possible. The smallest range for M would be 1, which would occur when a = 0 and b = 1.
In this case, the largest possible error in the approximation would be |P(0 < M < 1) - e|, where P(0 < M < 1) is the true probability and e is the approximation. In summary, the largest possible error you could make in approximating P(a < M < b) by e is when a = 0 and b = 1. The error would be |P(0 < M < 1) - e|.
More on errors: https://brainly.com/question/14281619
#SPJ11
You start driving west for 3 miles, turn right, and drive north for another 13 miles. At the end of driving, what is your straight line distance from your starting point? Round to the nearest tenth of a mile.
Answers
Answer:
13.3 miles to nearest 1/10.
Step-by-step explanation:
The journey forms a right triangle so by Pythagoras:
d^2 = 3^2 + 13^2
d^2 = 9 + 169
d^2 = 178
d = 13.34 miles.
Calculate the mass-volume percent of 5.0 g of magnesium chloride (MgCl2) in enough water to give 250 mL of solution.
Patulong po tysm!
Answers
Answer:
250*5.0=125.0
Step-by-step explanation:
250*5.0=125.0
Considering the definition of mass-volume percent, the mass-volume percent of 5.0 g of magnesium chloride in enough water to give 250 mL of solution is 2%.
Mass-volume percentMass-volume percent is a measure of concentration that indicates the number of grams of solute in each 100 mL of solution. It is an intensive property, that is, it does not depend on the amount of material.
Mass-volume percent is defined as the mass of solute in grams divided by the total volume of the solution in milliliters. To express this as a percent, we multiply this fraction by 100:
\(Mass-volume percent=\frac{mass of solute}{volume}x100\)
Mass-volume percent of magnesium chlorideIn this case, you know:
mass of solute= 5 gvolume= 250 mLReplacing in the definition of mass-volume percent:
\(Mass-volume percent=\frac{5 g}{250 mL}x100\)
Solving:
Mass-volume percent= 2%
Finally, the mass-volume percent of 5.0 g of magnesium chloride in enough water to give 250 mL of solution is 2%.
Learn more about mass-volume percent:
https://brainly.com/question/25486168
https://brainly.com/question/14707974
evaluate -6-(-5) x (-9)
Answers
That’s the answer
100 points please help!!

Answers
Answer: (5x-1)(x+4)
Step-by-step explanation:what she said
2x + 3y = 12
2x - y = 4
Answers
Answer:
The point of intersection between 2x+3y=12 and 2x-y=4 is (3,2)
Step-by-step explanation:
HELP PLEASE?? not sure about it!!

Answers
Can I know the answer for the above questions

Answers
Answer:
Step-by-step explanation:
I need help please!!!

Answers
\(\\ \bull\tt\dashrightarrow f(x)=6^x\)
\(\\ \bull\tt\dashrightarrow f(-2)=6^{-2}=\dfrac{1}{6^2}=\dfrac{1}{36}\)
\(\\ \bull\tt\dashrightarrow f(-1)=6^{-1}=\dfrac{1}{6}\)
\(\\ \bull\tt\dashrightarrow f(0)=6^0=1\)
\(\\ \bull\tt\dashrightarrow f(1)=6^1=6\)
\(\\ \bull\tt\dashrightarrow f(2)=6^2=36\)
what is the answer to -13v=182
Answers
-13v=182
-13 -13
v= -14
In body paragraph 1, how many times is evidence (‘SAY”) cited? B) Same article? Yes or No

Answers
Answer:
Down below hope it helps :)
Step-by-step explanation:
The evidence "SAY" was only written once. It wasn't by the same article, the writer introduces two separate articles.
Kinda confused by this question but I think that's the answer.
on a scaled drawing a building measers 4.5 cm tall if the scale drawing is 25 meters per 2 cm how tall is the actual building?
Answers
The actual building is tall 56.3 meters
How to calculate the height of the actual building ?
On a scaled drawing a building measures 4.5 cm tall
The scale drawing is 25 meters per 2 cm
The first step is to calculate the equivalent of 1 cm in meters
2 centimetres= 25 meters
1 centimetre= x
cross multiply both sides
2x= 25
x= 25/2
x= 12.5
1 centimetre is 12.5 metres
4.5 centimetres in metres is
= 4.5 × 12.5
= 56.3
Hence the height of the actual building is 56.3 meters
Read more on meters here
https://brainly.com/question/11911800
#SPJ1
Find the midpoint M of the line segment joining the points S = (-4,-2) and T = (6, -8).

Answers
We have that The midpoint M of the line segment joining the points
S = (-4,-2) T = (6, -8)is
\(M=(-3,-1)\)
From the question we are told
Find the midpoint M of the line segment joining the points
S = (-4,-2) T = (6, -8Generally the equation for the midpoint is is mathematically given as
\(M=\sqrt{\frac{x1+x2}{2},(y1+y2)^2}\\\\M=\frac{-4+-2}{2},\frac{(6+-8)}{2}}\)
\(M=(-3,-1)\)
Therefore
The midpoint M of the line segment joining the points
S = (-4,-2) T = (6, -8)is
\(M=(-3,-1)\)
For more information on this visit
https://brainly.com/question/23366835
( a + b ) ^ { - 1 } \cdot ( a ^ { - 1 } + b ^ { - 1 } )
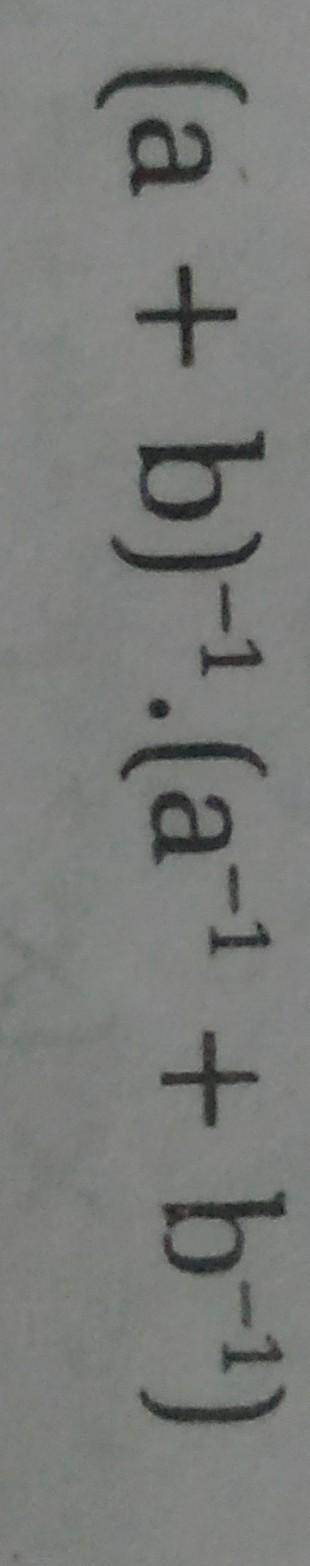
Answers
Answer:
don't know bro
sry
don't mind
<>
Determine the volume of the tent?

Answers
Answer:
6(base) x 3.5(Height) = 21, 21 divided by 2 (x 1/2) = 10.5
10.5(area of triangle) x 7.75(width) = 81.375
Formula of an area of a triangle:
BH x 1/2
Base x Height x 1/2(basically just dividing by 2)
Now the base:
1.5 x 7.75 x 6 = 69.75
Now let's add the two given volumes:
81.375+ 69.75 = 151.125 ft^3 is your answer.
I need help as fast as possible to get the answer.

Answers
To determine the algabraic equation that will represent the situation;
When you take a look at the diagram, when you trace 1x on the y-axis, it will fall on the second box. Each box represent 100 .
The y- axis falls on the one-fourth of the second box, which means its 125
Hence the algabraic equation to represent the situation is;
y= 125x
where x is the number of hours
and y represent the earnings
As for Part F, if you want to to determine Jerome earnings for a particular number of hours, just substitute the hours with the x and then solve for y.
What is the slope of the line and y intercept pls help me

Answers
Answer: c
Step-by-step explanation:
PLEASE BE A LIFE SAVERRR AND HELP ME ITS SO IMPORTANT

Answers
Answer:
a
Step-by-step explanation:
Please help me ASAPPPPPP
Answers
Answer:
Step-by-step explanation:
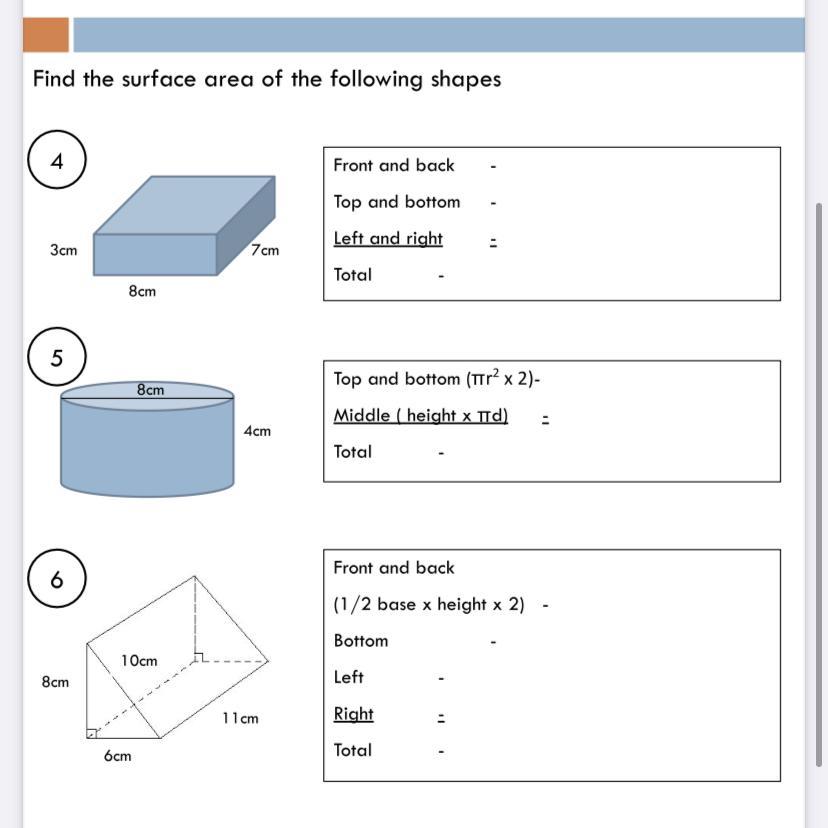
4). Surface area of front and back = 2(lengh × height)
= 2(7×3)
= 63 cm²
Surface area of top and bottom = 2(length × width)
= 2(8×7)
= 112 cm²
Surface area of left and right = 2(width × height)
= 2(8×3)
= 48 cm²
Total surface area = 63 + 112 + 48
= 223 cm²
5). Surface area of top and bottom = 2πr²
= 2π(4)²
= 32π
= 100.53 cm²
Surface area of middle = h(π × d)
= 4(π × 8)
= 32π
= 100.53 cm²
Total surface area = 32π + 32π
= 64π
= 201.06 cm²
6). Surface area of front and back = \(2[\frac{1}{2}(\text{Base})(\text{Height)}]\)
= Base × Height
= 6 × 8
= 48 cm²
Surface area of bottom = 6 × 11
= 66 cm²
Surface area of the left = 8 × 11
= 88 cm²
Surface area of right = 10 × 11
= 110 cm²
Total surface area = 48 + 66 + 88 + 110
= 312 cm²
David is making a rectangular exercise yard for his turtle, Ralph. The perimeter of the yard is
16x² + 12x +18
3x
2x² + 6x +9
3x
inches in total. The length of the yard measures
inches. Find an expression to represent the measure of the width in inches
Answers
yd=
yd=
16x2+12x+18=3x=2x2+6x+9=3x=
sorry i try
Answer:
D
Step-by-step explanation:
The positive variables p and c change with respect to time t. The relationship between p and c is given by the equation p2 (20 c). At the instant when 41 and c 15, what is the value ofC ? dc dt dt 3V5 2(D) 82V5 15 2V5 82 75 (B)
Previous question
Answers
The value of c at the instant when p=41 and dc/dt=15 is 2√82.
To solve for c at the given instant, we first take the derivative of the given equation with respect to t: \(2p(dp/dt)(20c)\) + \(p^2(20(dc/dt))\) = 0 We plug in p=41 and \(dc/dt=15\) and solve for \(dc/dt\):
\(2(41)(dp/dt)(20c) + (41)^2(20)(15)\) = 0
\(dp/dt = -(41c)/(60)\)
Now we can plug in \(p=41, dc/dt=15, and dp/dt=-(41c)/(60)\) to solve for c: \((41)^2 = -(41c)/(60)(20c)\) c = 2√82 Therefore, the value of c at the given instant is 2√82.
Learn more about derivative here:
https://brainly.com/question/29020856
#SPJ11
For the function f(x) = x³6x² + 12x - 11, find the domain, critical points, symmetry, relative extrema, regions where the function increases or decreases, inflection points, regions where the function is concave up and down, asymptotes, and graph it.
Answers
The function f(x) = x³6x² + 12x - 11 has a domain of all real numbers. The critical points of the function are found by setting the derivative equal to zero, resulting in x = -2 and x = 1 as the critical points.
The function is not symmetric. The relative extrema can be determined by evaluating the function at the critical points, resulting in a relative maximum at x = -2 and a relative minimum at x = 1. The function increases on the intervals (-∞, -2) and (1, ∞), and decreases on the interval (-2, 1). The inflection points can be found by setting the second derivative equal to zero, but in this case, the second derivative is a constant and does not equal zero, so there are no inflection points. The function is concave up on the intervals (-∞, -2) and (1, ∞), and concave down on the interval (-2, 1). There are no asymptotes. A graph of the function can visually represent these characteristics.
The domain of the function f(x) = x³6x² + 12x - 11 is all real numbers because there are no restrictions on the variable x.
To find the critical points, we need to find the values of x where the derivative f'(x) equals zero. Taking the derivative of f(x), we get f'(x) = 3x² - 12x + 12. Setting f'(x) equal to zero, we solve the quadratic equation 3x² - 12x + 12 = 0. Factoring it, we have 3(x - 2)(x - 1) = 0, which gives us the critical points x = -2 and x = 1.
The function is not symmetric because it does not satisfy the condition f(x) = f(-x) for all x.
To find the relative extrema, we evaluate the function at the critical points. Plugging in x = -2, we get f(-2) = -29, which corresponds to a relative maximum. Plugging in x = 1, we get f(1) = -4, which corresponds to a relative minimum.
The function increases on the intervals (-∞, -2) and (1, ∞) because the derivative f'(x) is positive in those intervals. It decreases on the interval (-2, 1) because the derivative is negative in that interval.
To find the inflection points, we need to find the values of x where the second derivative f''(x) equals zero. However, the second derivative f''(x) = 6 is a constant and does not equal zero, so there are no inflection points.
The function is concave up on the intervals (-∞, -2) and (1, ∞) because the second derivative f''(x) is positive in those intervals. It is concave down on the interval (-2, 1) because the second derivative is negative in that interval.
There are no asymptotes because the function does not approach infinity or negative infinity as x approaches any particular value.
A graph of the function can visually represent all the characteristics mentioned above, including the domain, critical points, relative extrema, regions of increase and decrease, concavity, and absence of asymptotes.
Learn more about critical points here:
https://brainly.com/question/32077588
#SPJ11