Answers
The differential equation
\(ay'' + by' + c = 0\)
has characteristic equation
\(ar^2 + br + c = 0\)
with roots \(r = \frac{-b\pm\sqrt{b^2-4ac}}{2a} = \frac{-b\pm\sqrt{D}}{2a}\).
• If \(D>0\), the roots are real and distinct, and the general solution is
\(y = C_1 e^{r_1x} + C_2 e^{r_2x}\)
• If \(D=0\), there is a repeated root and the general solution is
\(y = C_1 e^{rx} + C_2 x e^{rx}\)
• If \(D<0\), the roots are a complex conjugate pair \(r=\alpha\pm\beta i\), and the general solution is
\(y = C_1 e^{(\alpha+\beta i)x} + C_2 e^{(\alpha-\beta i)x}\)
which, by Euler's identity, can be expressed as
\(y = C_1 e^{\alpha x} \cos(\beta x) + C_2 e^{\alpha x} \sin(\beta x)\)
The solution curve in plot (A) has a somewhat periodic nature to it, so \(\boxed{D < 0}\). The plot suggests that \(y\) will oscillate between -∞ and ∞ as \(x\to\infty\), which tells us \(\alpha>0\) (otherwise, if \(\alpha=0\) the curve would be a simple bounded sine wave, or if \(\alpha<0\) the curve would still oscillate but converge to 0). Since \(\alpha\) is the real part of the characteristic root, and we assume \(a>0\), we have
\(\alpha = -\dfrac b{2a} > 0 \implies -b > 0 \implies \boxed{b < 0}\)
Since \(D=b^2-4ac<0\), we have
\(b^2 < 4ac \implies c > \dfrac{b^2}{4a} \implies \boxed{c>0}\)
The solution curve in plot (B) is not periodic, so \(D\ge0\). For \(x\) near 0, the exponential terms behave like constants (i.e. \(e^{rx}\to1\)). This means that
• if \(D>0\), for some small neighborhood around \(x=0\), the curve is approximately constant,
\(y = C_1 e^{r_1x} + C_2 e^{r_2x} \approx C_1 + C_2\)
• if \(\boxed{D=0}\), for some small neighborhood around \(x=0\), the curve is approximately linear,
\(y = C_1 e^{rx} + C_2 x e^{rx} \approx C_1 + C_2 x\)
Since \(D=b^2-4ac=0\), it follows that
\(b^2=4ac \implies c = \dfrac{b^2}{4a} \implies \boxed{c>0}\)
As \(x\to\infty\), we see \(y\to-\infty\) which means the characteristic root is positive (otherwise we would have \(y\to0\)), and in turn
\(r = -\dfrac b{2a} > 0 \implies -b > 0 \implies \boxed{b < 0}\)
Related Questions
A researcher posts a newspaper advertisement offering $10 in exchange for participation in a short study. The researcher accepts the first 10
people who respond to the advertisement. Which of the following statements is true about the sample?
A. It is not a valid sample because it is only a short study.
B. It is a valid sample because money is offered to participants.
C. It is a valid sample because the first 10 people were selected to participate.
D. It is not a valid sample because it is not a random sample of the population.
Answers
The correct answer is D: It is not a valid sample because it is not a random sample of the population.
For a sample to be valid and representative of the population, it should be selected randomly. In this case, the researcher accepted the first 10 people who responded to the advertisement. This is a non-random sampling method known as convenience sampling and is prone to biases.
The other statements are incorrect:
A) The length of the study does not affect whether the sample is valid.
B) Offering compensation does not automatically make the sample valid.
C) Selecting the first 10 people does not make the sample valid - it needs to be selected randomly.
So in summary, the key issue here is that the sample was not selected randomly from the population, making it not a valid representative sample.
Prove that
(secx+tanx)² =CSCx+1/CSC x-1

Answers
To prove that (secx+tanx)² = (cscx+1)/(cscx-1), we will start with the left-hand side (LHS) of the equation and simplify it step by step until it matches the right-hand side (RHS) of the equation.
LHS: (secx+tanx)²
Using the trigonometric identities secx = 1/cosx and tanx = sinx/cosx, we can rewrite the LHS as:
LHS: (1/cosx + sinx/cosx)²
Now, let's find a common denominator and simplify:
LHS: [(1+sinx)/cosx]²
Expanding the squared term, we get:
LHS: (1+sinx)² / cos²x
Next, we will simplify the denominator:
LHS: (1+sinx)² / (1 - sin²x)
Using the Pythagorean identity sin²x + cos²x = 1, we can replace 1 - sin²x with cos²x:
LHS: (1+sinx)² / cos²x
Now, let's simplify the numerator by expanding it:
LHS: (1+2sinx+sin²x) / cos²x
Next, we will simplify the denominator by using the reciprocal identity cos²x = 1/sin²x:
LHS: (1+2sinx+sin²x) / (1/sin²x)
Now, let's simplify further by multiplying the numerator and denominator by sin²x:
LHS: sin²x(1+2sinx+sin²x) / 1
Expanding the numerator, we get:
LHS: (sin²x + 2sin³x + sin⁴x) / 1
Now, let's simplify the numerator by factoring out sin²x:
LHS: sin²x(1 + 2sinx + sin²x) / 1
Using the fact that sin²x = 1 - cos²x, we can rewrite the numerator:
LHS: sin²x(1 + 2sinx + (1-cos²x)) / 1
Simplifying further, we get:
LHS: sin²x(2sinx + 2 - cos²x) / 1
Using the fact that cos²x = 1 - sin²x, we can rewrite the numerator again:
LHS: sin²x(2sinx + 2 - (1-sin²x)) / 1
Simplifying the numerator, we have:
LHS: sin²x(2sinx + 1 + sin²x) / 1
Now, let's simplify the numerator by expanding it:
LHS: (2sin³x + sin²x + sin²x) / 1
LHS: 2sin³x + 2sin²x / 1
Finally, combining like terms, we get:
LHS: 2sin²x(sin x + 1) / 1
Now, let's simplify the RHS of the equation and see if it matches the LHS:
RHS: (cscx+1) / (cscx-1)
Using the reciprocal identity cscx = 1/sinx, we can rewrite the RHS:
RHS: (1/sinx + 1) / (1/sinx - 1)
Multiplying the numerator and denominator by sinx to simplify, we get:
RHS: (1 + sinx) / (1 - sinx)
Now, we can see that the LHS and RHS are equal:
LHS: 2sin²x(sin x + 1) / 1
RHS: (1 + sinx) / (1 - sinx)
Therefore, we have proven that (secx+tanx)² = (cscx+1)/(cscx-1).
For more such questions on prove, click on:
https://brainly.com/question/30831725
#SPJ8
Following are the introduced the accompanying observations on bond strength.
11.5 12.1 9.9 9.3 7.8 6.2 6.6 7.0 13.4 17.1 9.3 5.6 5.7 5.4 5.2 5.1 4.9 10.7
15.2 8.5 4.2 4.0 3.9 3.8 3.6 3.4 20.6 25.5 13.8 12.6 13.1 8.9 8.2 10.7 14.2
7.6 5.2 5.5 5.1 5.0 5.2 4.8 4.1 3.8 3.7 3.6 3.6 3.6
Required:
Estimate true average bond strength in a way that conveys information about precision and reliability.
Answers
Answer:
Average strength of bond = 8.08 (Approx.)
Step-by-step explanation:
Given data;
11.5 12.1 9.9 9.3 7.8 6.2 6.6 7.0 13.4 17.1 9.3 5.6 5.7 5.4 5.2 5.1 4.9 10.7 15.2 8.5 4.2 4.0 3.9 3.8 3.6 3.4 20.6 25.5 13.8 12.6 13.1 8.9 8.2 10.7 14.2 7.6 5.2 5.5 5.1 5.0 5.2 4.8 4.1 3.8 3.7 3.6 3.6 3.6
Find:
Average strength of bond
Computation:
Average mean = Sum of all observation / Number of observation
Average strength of bond = [11.5 + 12.1 + 9.9 + 9.3 + 7.8 + 6.2 + 6.6 + 7.0 + 13.4 + 17.1 + 9.3 + 5.6 + 5.7 + 5.4 + 5.2 + 5.1 + 4.9 + 10.7 + 15.2 + 8.5 + 4.2 + 4.0 + 3.9 + 3.8 + 3.6 + 3.4 + 20.6 + 25.5 + 13.8 + 12.6 + 13.1 + 8.9 + 8.2 + 10.7 + 14.2 + 7.6 + 5.2 + 5.5 + 5.1 + 5.0 + 5.2 + 4.8 + 4.1 + 3.8 + 3.7 + 3.6 + 3.6 + 3.6] / 48
Average strength of bond = [387.8] / 48
Average strength of bond = 8.0791
Average strength of bond = 8.08 (Approx.)
How many different possible outcomes are there if you flip seven coins?
Answers
Answer:
Because the coin is tossed 7 times and you get 2 outcomes (head or tail) for each one.
i need a y=mx+b problem

Answers
Answer: y=x^2
Step-by-step explanation: There are first of all squares, so you have to multiply the sides. Well and the figure 2 has a side of two smaller squares. So you know x is the argument, in this case the number of the figure, because it is regularly you know that x as example for figure 7 is seven so you have to multiply 7 by 7. This isn’t linear.
Educators should ensure math instruction is only taught through structured activities rather than through everyday situations and routines.
A- True
B- False
Answers
The statement ' educators should ensure math instruction is only taught through structured activities rather than through everyday situations and routines is True. Option A
Ways to improve mathematics education
They include;
Using hands-on learning methodsUsing visualsIntegration of mathematics gameConnecting math concepts to everyday lifeAllow students to explain their reasoningRewarding students progressThus, the statement ' educators should ensure math instruction is only taught through structured activities rather than through everyday situations and routines is True. Option A
Learn more about early childhood education here:
https://brainly.in/question/7275502
#SPJ1
Answer:
Step-by-step explanation:
false
please simplify this! whoever gets its correct i will mark your comment as a brainliest !

Answers
Answer:
Step-by-step explanation:
6x^8 X y^5
4x^5 X z^8
12a^9 X b^7
6s^9 X t^3
20/5 as a whole number
Answers
Answer:
4 is the answer
Step-by-step explanation:
Given 3 + 7 + 11 + 15 + … find S20
Answers
Answer:
Hi
Please mark brainliest ❣️
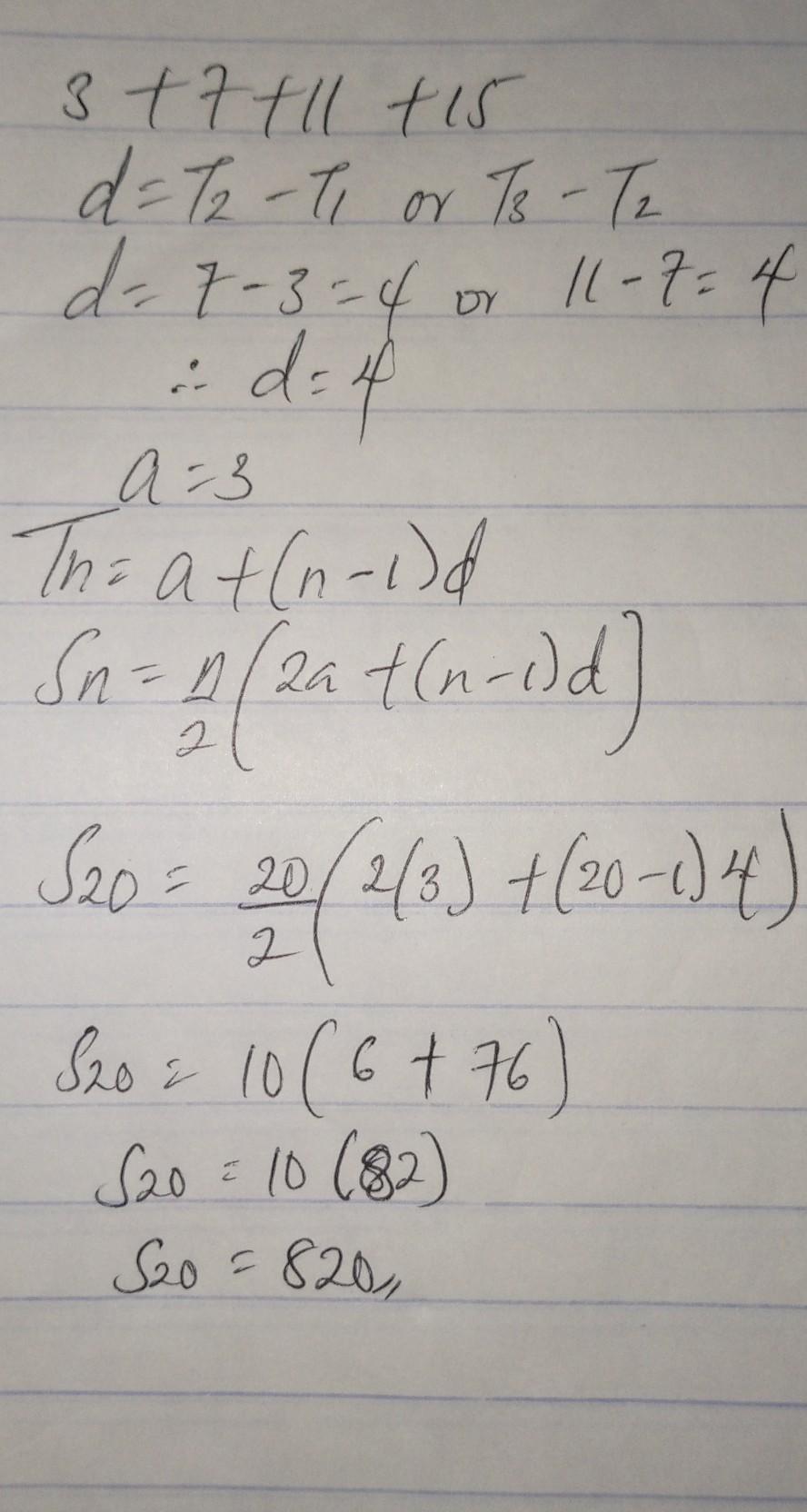
Evaluate f(x) = 1/4x for x = -5.
A. 20
B. -1/20
C. -1 1/4
D. -4/5
Answers
Answer: C
Step-by-step explanation:
1/4th of -5 is -1.25 so in fractions that is -1 1/4 (ANSWER IS C)
the answer is C
19. What do you mean by linear programming model? A person requires minimum 10, 12 and 12 units of chemicals A, B and C respectively. A liquid product contains 5, 2 and 1 units of A, B and C per jar. A dry product contains 1, 2 and 4 units of A, B and C per carton. If the liquid product costs Rs 30 per jar and dry product costs Rs 20 per carton. Formulate this problem in linear programming model. How many of each product should be purchased in order to minimize the cost to meet the requirements. Also find the minimum cost.
Answers
Answer:
the cos is Rs 20 per jar and dry
Need help ASAP
the value of each variable. If your answer is not
teger, express it in simplest radical form.
The length of a is
The length of b is
(Simplify your answer.)

Answers
Answer:
me too (help)
Step-by-step explanation:
The running back for the Bulldogs football team carried the ball 7 times for a total loss of 12 1/4 yards. Find the average change in field position on each run. Enter the average change as a simplified mixed number.
Answers
The average change as a simplified mixed number would be,
⇒ 1 3/4
A fraction is a part of whole number, and a way to split up a number into equal parts. Or, A number which is expressed as a quotient is called fraction. It can be written as the form of p : q, which is equivalent to p / q.
We have to given that;
The running back for the Bulldogs football team carried the ball 7 times for a total loss of 12 1/4 yards.
Now, The average change as a simplified mixed number would be,
⇒ (12 1/4) / 7
⇒ (49/4) / 7
⇒ (49 / 4×7)
⇒ 7/4
⇒ 1 3/4
Therefore, The average change is,
⇒ 1 3/4
Learn more about the divide visit:
https://brainly.com/question/28119824
#SPJ1
If A represents the hypotenuse of this right triangle, which equation could
you use to find the value of A?

Answers
Answer:
its option D......im 100 percent sure
Answer:
d
Step-by-step explanation:
If you know the answer put and explanation for it please thank you

Answers
Answer:
14 students have to retake the test
Step-by-step explanation:
to calculate the mean mark as
sum of ( product of mark and frequency ) ÷ total
mean = \(\frac{14(2)+15(10)+16(2)+17(3)+18(13)}{30}\)
= \(\frac{28+150+32+51+234}{30}\)
= \(\frac{495}{30}\)
= 16.5
students who score less than 16.5 will retake the test , that is
2 scored 16 , 10 scored 15 , 2 scored 14
number who have to retake test = 2 + 10 + 2 = 14
−1/5(x−4)=−2 Please help me fast
Answers
Answer:
x=14
Step-by-step explanation:
Step 1: Simplify both sides of the equation.
−1/5(x−4)=−2
(−1/5)(x)+(−1/5)(−4)=−2(Distribute)
−1/5x+4/5=−2
Step 2: Subtract 4/5 from both sides.
−1/5x+4/5−4/5=−2−4/5
−1/5x=−14/5
Step 3: Multiply both sides by 5/(-1).
(5/−1)*(−1/5x)=(5/−1)*(−14/5)
∫∫(x+y)dxdy ,d là miền giới hạn bởi x²+y²=1
Answers
It looks like you want to compute the double integral
\(\displaystyle \iint_D (x+y) \,\mathrm dx\,\mathrm dy\)
over the region D with the unit circle x ² + y ² = 1 as its boundary.
Convert to polar coordinates, in which D is given by the set
D = {(r, θ) : 0 ≤ r ≤ 1 and 0 ≤ θ ≤ 2π}
and
x = r cos(θ)
y = r sin(θ)
dx dy = r dr dθ
Then the integral is
\(\displaystyle \iint_D (x+y)\,\mathrm dx\,\mathrm dy = \iint_D r^2(\cos(\theta)+\sin(\theta))\,\mathrm dr\,\mathrm d\theta \\\\ = \int_0^{2\pi} \int_0^1 r^2(\cos(\theta)+\sin(\theta))\,\mathrm dr\,\mathrm d\theta \\\\ = \underbrace{\left( \int_0^{2\pi}(\cos(\theta)+\sin(\theta))\,\mathrm d\theta \right)}_{\int = 0} \left( \int_0^1 r^2\,\mathrm dr \right) = \boxed{0}\)
Please answer this correctly

Answers
Answer:
the answer is 45 because there are four marbles so it would be a 50/50
Explanation: there’s an equal amount of purple and green marbles, so if you select a marble 84 times, the best prediction possible would be selecting 42 purple marbles.
Carefree offers two type of care packages. The food packages sell for 20$ and the game packages sell for 32$. In one day Carefree sold 25 Care packeges. the receipt for those packages totaled 602$ How many of each type of package were sold
Answers
Answer:
Number of game package = 16.5
Number of food package = 8.5
Step-by-step explanation:
LET :
Food package = a
Game package = b
a + b = 25 - - - (1)
20a + 32b = 602 - - - (2)
a = 25 - b
Put a = 25 - b into (2)
20(25 - b) + 32b = 602
500 - 20b + 32b = 602
12b = 102
b = 102 / 12
b = 8.5
a = 25 - b
a = 25 - 8.5
a = 16.5
Number of game package = 16.5
Number of food package = 8.5
A shopper paid 11/100 of a dollar for 1/16 of a kilogram of nails. What was the rate in dollars per
kilograms?
Answers
Answer:
\(Rate = \$1.76/kg\)
Step-by-step explanation:
Given
\(\frac{1}{16}kg\) of nails costs \(\$ \frac{11}{100}\)
Required
Determine the rate
The rate, in this case, will be calculated as:
\(Rate = \frac{amount}{weight}\)
\(Rate = \frac{\frac{11}{100}}{\frac{1}{16}}\)
This gives
\(Rate = \frac{11}{100}/\frac{1}{16}\)
\(Rate = \frac{11}{100} * 16\)
\(Rate = \frac{176}{100}\)
\(Rate = \$1.76/kg\)
Answer:
Answer:
Step-by-step explanation:
Given
of nails costs
Required
Determine the rate
The rate, in this case, will be calculated as:
This gives
Step-by-step explanation:
Question
Simplify the expression:
(4/9)^3
Answers
Answer:
Step-by-step explanation:
(4^3/(9^3)
= 64/729 or0.09
Write an expression that represents the perimeter of the triangle.

Answers
Answer:
(3m - 2) + (2m + 7) + (5m - 3)
Step-by-step explanation:
Perimeter is found by combining all side measurements together to find the total measurement. In this case, combine the sides:
(3m - 2) + (2m + 7) + (5m - 3) is your answer.
If you need a simplified expression, simply combine all the like terms together. Like terms are terms with the same as well as same amount of variables:
(3m + 2m + 5m) + (7 - 2 - 3)
(10m) + (2)
10m + 2 is your answer.
~
ASAP!!! Answer the following include all steps

Answers
Question 1:
(a) The equation representing Elaine's total parking cost is:
C = x * t
(b) So the cost of parking for a full 24 hours would be 24 times the cost per hour.
Question 2:
The given system of equations is inconsistent and has no solution.
(a) To represent Elaine's total parking cost, C, in dollars for t hours, we need to know the cost per hour. Let's assume the cost per hour is $x.
(b) If Elaine wants to park her car for a full 24 hours, we can substitute t = 24 into the equation from part (a):
C = x * 24
Question 2:
To solve the linear system:
-x - 6y = 5
x + y = 10
We can use the elimination method.
Multiply the second equation by -1 to create opposites of the x terms:
-x - 6y = 5
-x - y = -10
Add the two equations together to eliminate the x term:
(-x - 6y) + (-x - y) = 5 + (-10)
-2x - 7y = -5
Now we have a new equation:
-2x - 7y = -5
To check the answer, we can substitute the values of x and y back into the original equations:
From the second equation:
x + y = 10
Substituting y = 3 into the equation:
x + 3 = 10
x = 10 - 3
x = 7
Checking the first equation:
-x - 6y = 5
Substituting x = 7 and y = 3:
-(7) - 6(3) = 5
-7 - 18 = 5
-25 = 5
For more such questions on parking cost
https://brainly.com/question/18091509
#SPJ8
Solve the following system of equations with the substitution method:
y=3/5x-15
y=-3/4x+12
Answers
Answer:
x = 20, y = -3
Step-by-step explanation:
Set both equations equal to each other
\(\displaystyle y=\frac{3}{5}x-15\\\\y=-\frac{3}{4}x+12\\\\\\\\\frac{3}{5}x-15=-\frac{3}{4}x+12\\\\\frac{12}{20}x-15=-\frac{15}{20}x+12\\\\\frac{27}{20}x-15=12\\\\\frac{27}{20}x=27\\\\x=20\\\\y=\frac{3}{5}x-15\\\\y=\frac{3}{5}(20)-15\\\\y=\frac{60}{5}-15\\\\y=12-15\\\\y=-3\)
Ayudaaaaaaaaaaa.............

Answers
Es la repuesta
Use the scale drawing to determine how wide the duck pond is? A. 18 feet B. 27 feet C. 49.5 feet D. 55.5 feet
Answers
The width of the duck pond is,
⇒ 27 feet
We can see that the given diagram is a rectangle,
And we know that,
Rectangles are four-sided polygons with all internal angles equal to 90 degrees. At each corner or vertex, two sides meet at right angles. The rectangle differs from a square in that its opposite sides are equal in length.
Now, By given diagram we have;
We have to given that;
Use the scale drawing to determine how wide the duck pond is.
And there are 4.5 feet in 1 square,
Therefore,
1 square is equal to 4.5 feet
So, we get;
The width of the duck pond is,
⇒ 6 square
We know that,
To multiply means to add a number to itself a particular number of times. Multiplication can be viewed as a process of repeated addition.
Then to find width of duck pond in feet,
Multiply 6 with 4.5
⇒ 6 × 4.5 feet
⇒ 27 feet
Thus, The width of the duck pond is,
⇒ 27 feet
Learn more about the multiplication visit:
brainly.com/question/10873737
#SPJ1

VI. In a class of 40 students, the marks obtained in Mathematics (out of 50) are as under: 44,50,44,49,42,47,45,42,44,48,49,48,47 49,47,41,45,48,41,48,41,42,47,49,49,48, 50.47.49.48.46.44.45.45.46.44.42.47.48.45 ow answer the following questions: a) b) c) d) e) Find the number of students getting more than 45 marks. Find the number of students getting less than 45 marks. Find the maximum number of students getting the same marks. Find the average marks obtained by the students in the class. Find the number of students getting more than average marks.
Answers
a) To find the number of students getting more than 45 marks, we count the students whose marks are greater than 45 in the given list.
In the given list, the students with marks greater than 45 are: 50, 49, 47, 48, 49, 48, 47, 49, 48, 50, 47, 49, 48, 46, 47, 48, 47.
Counting these numbers, we find that there are 17 students who obtained more than 45 marks.
b) To find the number of students getting less than 45 marks, we count the students whose marks are less than 45 in the given list.
In the given list, the students with marks less than 45 are: 44, 44, 42, 41, 41, 42, 41, 44, 44, 42, 45, 45, 45, 44, 45.
Counting these numbers, we find that there are 15 students who obtained less than 45 marks.
c) To find the maximum number of students getting the same marks, we look for the mark that appears most frequently in the given list.
In the given list, the marks obtained by the students are: 44, 50, 44, 49, 42, 47, 45, 42, 44, 48, 49, 48, 47, 49, 47, 41, 45, 48, 41, 48, 41, 42, 47, 49, 49, 48, 50, 47, 49, 48, 46, 44, 45, 45, 46, 44, 42, 47, 48, 45.
Counting the frequency of each mark, we find that the marks 47 and 48 appear most frequently, with a count of 6 each. Therefore, the maximum number of students getting the same marks is 6.
d) To find the average marks obtained by the students in the class, we sum up all the marks and divide by the total number of students.
Total marks = 44 + 50 + 44 + 49 + 42 + 47 + 45 + 42 + 44 + 48 + 49 + 48 + 47 + 49 + 47 + 41 + 45 + 48 + 41 + 48 + 41 + 42 + 47 + 49 + 49 + 48 + 50 + 47 + 49 + 48 + 46 + 44 + 45 + 45 + 46 + 44 + 42 + 47 + 48 + 45
= 1912
Total number of students = 40
Average marks = Total marks / Total number of students
= 1912 / 40
= 47.8
Therefore, the average marks obtained by the students in the class is 47.8.
e) To find the number of students getting more than the average marks, we count the students whose marks are greater than 47.8.
In the given list, the students with marks greater than 47.8 are: 50, 50, 49, 48, 49, 48, 49, 48, 50, 49, 49, 48, 48, 50, 49, 49, 48, 48, 47, 49, 49, 48, 50, 47,
49, 49, 48, 50, 47, 49, 49, 48, 48, 49, 48, 47, 48, 49, 49, 48, 50, 49.
Counting these numbers, we find that there are 40 students who obtained more than the average marks.
please help! What is the exact volume of the cylinder?
Enter your answer, in terms of π, in the box.

Answers
\(\pi \: {r}^{2} h\)
\( \frac{22}{7} \times \: {5}^{2} \times 15\)
\(1178.09725\)
pls HELP ME ASAP DUE TODAY NOW HURRY PLEASE

Answers
Answer: so yea its the first one. im not that sure im just like saying what I know
Step-by-step explanation:
What is the zero of r(x)
=
8/3X-16
Answers
Answer:
x = 6
Step-by-step explanation:
(8/3)x - 16 = 0
Add 16 to both sides
(8/3)x = 16
Multiply both sides by 3/8
x = 16(3/8)
x = 6
