Answers
\(\text{Endpoints of diameter,}~~ A(4,6)~ \text{and}~ B(-3,-1)\\\\\text{Diameter,}~AB = \sqrt{(4+3)^2+(6+1)^2}\\\\~~~~~~~~~~~~~~~~~~~=\sqrt{7^2+7^2}\\\\~~~~~~~~~~~~~~~~~~~=7\sqrt2\\\\\text{So , radius}~ = \dfrac{AB}2 = \dfrac{7\sqrt 2}2 =4.9~\text{units.}\\\\\text{Hence the answer is B.}\)
Related Questions
the cost in dollars of a class party is 59 13n, where n is the number of people attending. what is the cost for 44 people?
Answers
The total cost of 44 people in the class party will be $631
The total cost in dollars of a class party is 59 + 13n
Where n = number of people attending in the class party
Let F(n) be the function representing the total cost in dollars of a class party
Such as, F(n) = 59 + 13n
As per the question, the total cost of attending the 44 people will be:
For 44 people we have n = 44
As we had, F(n) = 59 + 13n
Here, F(n) will be treated as a function in which n will be its domain while F(n) will give the output as a range.
F(44) = 59 + 13(44)
= 59 + 572
= 631
Total cost will be $631
To learn more on input and output of a function, visit here:
https://brainly.com/question/13221237
#SPJ4
let an = 8n 4n 1 . (a) determine whether {an} is convergent.
Answers
The sequence {an} = {\(8n^4 + n + 1\)} is not convergent. It diverges to infinity as n approaches infinity.
To determine whether the sequence {an} = {\(8n^4 + n + 1\)} is convergent, we need to examine the behavior of the terms as n approaches infinity.
The sequence {an} is said to be convergent if there exists a real number L such that the terms of the sequence get arbitrarily close to L as n approaches infinity.
To investigate convergence, we can calculate the limit of the sequence as n approaches infinity.
lim(n→∞) \((8n^4 + n + 1)\)
To evaluate this limit, we can look at the highest power of n in the sequence, which is \(n^4.\) As n approaches infinity, the other terms (n and 1) become insignificant compared to n^4.
Taking the limit as n approaches infinity:
lim(n→∞) \(8n^4 + n + 1\)
= lim(n→∞) \(8n^4\)
Here, we can clearly see that the limit goes to infinity as n approaches infinity.
Therefore, the sequence {an} = {\(8n^4 + n + 1\)} is not convergent. It diverges to infinity as n approaches infinity.
To learn more about limit of the sequence visit:
brainly.com/question/30647793
#SPJ11
Bobby drove 10 miles, and
his car used up 5 gallons of
gas. How many miles can
he drive with 16 gallons of
gas?
Answers
Answer:
32
Step-by-step explanation:
10/5 = 2 you go 2 miles per gallon of gas
there for 16*2= 32 miles on 16 gallons of gas
If all observations have a residual of 0, which of the following statements is true?
Choose the correct answer below.
A. The correlation coefficient will be 0.
B. The R-square will be 1.
C. The slope of the regression line will be 1.
D. An error was made in the calculation as a residual cannot be zero.
Answers
Answer: B
Which graph shows a proportional relationship

Answers
Answer:
i say d
Step-by-step explanation:
suppose that the population of all north american domesticated cats have a mean weight of 12 pounds and standard deviation of 2.5 pounds. the frequency distribution of north american domesticated cat weights is approximately normal. about 95% of the mean weights from samples of size 100 cats from this population fall between what two values (note: assume the sampling distribution of sample means is approximately normal)?
Answers
Answer. The correct option is (E). 9.5 and 14.5
Explanation for step 1This is because 95% of the mean weights from samples of size 100 cats from this population will fall between 9.5 and 14.5 pounds. The other answers are incorrect because they do not fall within the range of 95% of the mean weights from samples of size 100 cats from this population
About 95% of the mean weights from samples of size 100 cats from this population would fall between approximately 11.51 pounds and 12.49 pounds.
To determine the range within which 95% of the mean weights from samples of size 100 cats would fall, we can use the concept of the confidence interval.
Given:
Population mean weight (μ) = 12 pounds
Population standard deviation (σ) = 2.5 pounds
Sample size (n) = 100 cats
Since the population distribution is assumed to be approximately normal, the sampling distribution of sample means will also be approximately normal. To calculate the range, we can use the formula for the confidence interval:
Confidence Interval = sample mean ± (z * standard error)
The standard error can be calculated using the formula:
Standard Error = σ / √n
Using a 95% confidence level, the corresponding z-value is approximately 1.96 (obtained from standard normal distribution table).
Plugging in the values:
Standard Error = 2.5 / √100 = 0.25
Confidence Interval = 12 ± (1.96 * 0.25)
Calculating the values:
Lower limit = 12 - (1.96 * 0.25) ≈ 11.51 pounds
Upper limit = 12 + (1.96 * 0.25) ≈ 12.49 pounds
Know more about mean weights here:
https://brainly.com/question/16170417
#SPJ11
4. Evaluate: (-7 - 41)(8 - 6) A) -32 + 10i C) -80 - 10i B) -80 - 10i D) -32 + 741
help me please
Answers
Answer:
Step-by-step explanation:
(-7-41)(8-6)
-48*2
-96
This is what I got. I don't see anything in the equation that has "i" in it.
If it is supposed to be (-7-4i)(8-6) foil the problem.
-56+42-32i+24i combine like terms
the answer is -14-8i
2. match the type of center to the segments used to it. 1. orthocenter 2. centroid 3. incenter 4. circumcenter a. perpendicular bisectors b. angle bisectors c. altitudes d. medians
Answers
The orthocenter is determined by the intersection of altitudes, the centroid is determined by the intersection of medians, the incenter is determined by the intersection of angle bisectors, and the circumcenter is determined by the intersection of perpendicular bisectors.
1. Orthocenter: The orthocenter of a triangle is the point of intersection of the altitudes. An altitude is a line segment drawn from a vertex of the triangle perpendicular to the opposite side. The orthocenter does not necessarily lie inside the triangle; it can be inside, outside, or on the triangle itself.
2. Centroid: The centroid of a triangle is the point of intersection of the medians. A median is a line segment drawn from a vertex of the triangle to the midpoint of the opposite side. The centroid always lies inside the triangle and divides each median into two segments, with the ratio of 2:1 from the vertex to the midpoint
3. Incenter: The incenter of a triangle is the point of intersection of the angle bisectors. An angle bisector is a line segment that divides an angle into two equal angles. The incenter always lies inside the triangle and is equidistant from the three sides of the triangle.
4. Circumcenter: The circumcenter of a triangle is the point of intersection of the perpendicular bisectors. A perpendicular bisector is a line segment that is perpendicular to a side of the triangle and passes through its midpoint. The circumcenter is the center of the circle that circumscribes the triangle, and it can be inside, outside, or on the triangle itself.
Learn more about Centroid here:
https://brainly.com/question/10708357
#SPJ11
SOMEONE PLZ HELP ME ASAP!!!!
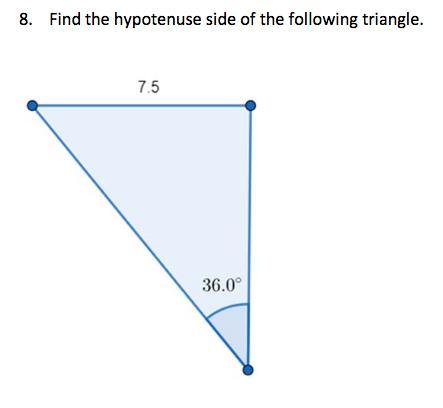
Answers
Answer:
hyp=12.76
Step-by-step explanation:
sin36=opp/hyp
hyp=opp/sin36
hyp=7.5/sin36
hyp=12.76 rounded to the nearest hundredth
A study conducted by the Center for Population Economics at the University of Chicago studied the birth weights of 682 babies born in New York. The mean weight was 3272 grams with a standard deviation of
896 grams. Assume that birth weight data are approximately bell-shaped. Estimate the number of newborns who weighed between 1480 grams and 5064 grams. Round to the nearest whole number.
The number of newborns who weighed between
1480 grams and 5064
grams is.
Answers
The number of newborns who weighed between 1480 grams and 5064 grams is approximately 650.
Given that, mean weight = 3272 grams
Standard deviation = 896 grams
We need to estimate the number of newborns who weighed between 1480 grams and 5064 grams. Therefore, we have to find the area under the normal curve from x = 1480 grams to x = 5064 grams. So, we have to find P(1480 < x < 5064)P(Z < (5064 - 3272)/896) - P(Z < (1480 - 3272)/896)
Using standard normal tables, we can find the probabilities that correspond to the z-values:
P(Z < (5064 - 3272)/896) = P(Z < 2.00)
= 0.9772P(Z < (1480 - 3272)/896)
= P(Z < -2.00)
= 0.0228P(1480 < x < 5064)
= 0.9772 - 0.0228 = 0.9544
We know that the total area under the normal curve is 1. Therefore, the number of newborns who weighed between 1480 grams and 5064 grams is:
Number of newborns = 0.9544 × 682≈ 650 (rounded to the nearest whole number).
You can learn more about Standard deviation at: brainly.com/question/29115611
#SPJ11
sum of independent negative binomial random variable and geometric random variable
Answers
The sum of independent negative binomial and geometric random variables does not have a closed-form distribution and must be computed numerically.
What is binomial random variable ?
In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: success or failure.
Let X be a negative binomial random variable with parameters r and p, and let Y be a geometric random variable with parameter q. The sum Z = X + Y is also a random variable.
The cumulative distribution function (CDF) of Z is given by:
F_Z(z) = P(Z <= z) = P(X + Y <= z) = ∑_{x=0}^{z} P(X = x) * P(Y = z - x)
This expression is a double sum and does not have a closed-form solution, but it can be computed numerically.
Alternatively, the probability mass function (PMF) of Z can be found by counting the number of ways that X and Y can take on their respective values, and summing up their joint probabilities:
f_Z(z) = P(Z = z) = ∑_{x=0}^{z} P(X = x) * P(Y = z - x)
The sum of independent negative binomial and geometric random variables does not have a closed-form distribution and must be computed numerically.
To learn more about binomial random variable visit : brainly.com/question/14282621
#SPJ4
Sketch The Graphs:
y = -1/3x -2
Answers
Answer:
Step-by-step explanation:

The graph of the straight line \(y = -\frac{1}{3}x -2\) is plotted. The graph is shown below.
A straight line is of the form y = mx + c, where m is the slope and c is the y-intercept.
To plot the given straight line \(y = -\frac{1}{3}x -2\), follow the following steps:
Step 1: Substitute x = 0 in the given equation to obtain the point where the line intersects the y-axis.
y = 0 - 2
y = -2
The point at the y-axis is (0, -2).
Step 2: Substitute y = 0 in the given equation to obtain the point where the line intersects the x-axis.
\(0 = -\frac{1}{3}x -2\\x = -6\)
The point at the x-axis is (-6, 0).
Step 3: Draw a straight line passing through both points.
Thus, the straight line \(y = -\frac{1}{3}x -2\) is plotted.
Learn more about Straight Line here;
https://brainly.com/question/31693341
#SPJ3

Darnell has
345
buttons to sew on shirts. Each shirt needs
12
buttons.
How many shirts can Darnell complete with the buttons he has?
Answers
Answer:
28
Step-by-step explanation:
Explanation: you would be short of a few buttons to make 29 but you can make 28 complete shirts
how to add Numbers with indices

Answers
Answer:
Just expand or simplify them then you should add.
Step-by-step explanation:
Example 8² = 64 and \(\sqrt{100}\) = 10
64 + 10 = 74
What general direction did Lin walk from the gym to his house, and what type of triangle did his walking path form? Lin walked south, creating a right triangle. Lin walked southwest, creating an obtuse triangle. Lin walked southeast, creating an acute triangle. Lin walked directly east, creating a right triangle.
Answers
The correct statement is ''Lin can walk southwest by creating an obtuse triangle to reach his house from the gym'' and it can be determined by using the properties of triangle.
We have to determine
What general direction did Lin walk from the gym to his house, and what type of triangle did his walking path form?
According to the question,
Types of Triangle;1. Lin walked south, creating a right triangle-
When someone walked in only one direction then a straight line is made by him over his path.
Here Lin can not make a right triangle just by walking in one direction.
Thus statement 1 is incorrect.
2. Lin walked southwest, creating an obtuse triangle.
When someone wants to reach a diagonal direction he can use either the right angle triangle path or the obtuse triangle.
Lin can walk southwest by creating an obtuse triangle to reach his house from the gym.
Thus statement 2 is correct.
3. Lin walked southeast, creating an acute triangle.
Actuate triangle is a triangle in which all three angles are less than the right angles (90 degrees).
With walking in actuate triangle one can make Lin can not go in his diagonal direction.
Thus statement 3 is incorrect.
4. Lin walked directly east, creating a right triangle.
When someone walked in only one direction then a straight line is made by him over his path.
Here Lin can not make a right triangle just by walking in one direction.
Thus statement 4 is incorrect.
Hence, Lin can walk southwest by creating an obtuse triangle to reach his house from the gym. Thus statement 2 is correct.
For more details about the Equation refer to the link given below.
https://brainly.com/question/9719077
Answer:
its B Lin walked southwest, creating an obtuse triangle
Solve the following systems of equations using Gaussian Elimination. 2x + 3y + z = 2 y + 5z = 20 -x+2y+3z = 13
Find the inner product of two vectors A = (2, -3,0) and B = = (-1,0,5)
Answers
The inner product of two vectors A = (2, -3,0) and B = (-1,0,5) is -2 / √(13×26).
Solving the given system of equations using Gaussian elimination:
2x + 3y + z = 2 y + 5z = 20 -x+2y+3z = 13
Matrix form of the system is
[A] = [B] 2 3 1 | 2 0 5 | 20 -1 2 3 | 13
Divide row 1 by 2 and replace row 1 by the new row 1: 1 3/2 1/2 | 1
Divide row 2 by 5 and replace row 2 by the new row 2: 0 1 1 | 4
Divide row 3 by -1 and replace row 3 by the new row 3: 0 0 1 | 5
Back substitution, replace z = 5 into second equation to solve for y, y + 5(5) = 20 y = -5
Back substitution, replace z = 5 and y = -5 into the first equation to solve for x, 2x + 3(-5) + 5 = 2 2x - 15 + 5 = 2 2x = 12 x = 6
The solution is (x,y,z) = (6,-5,5)
Therefore, the solution to the given system of equations using Gaussian elimination is (x,y,z) = (6,-5,5).
The given two vectors are A = (2, -3,0) and B = = (-1,0,5). The inner product of two vectors A and B is given by
A·B = |A||B|cosθ
Given,A = (2, -3,0) and B = (-1,0,5)
Magnitude of A is |A| = √(2²+(-3)²+0²) = √13
Magnitude of B is |B| = √((-1)²+0²+5²) = √26
Dot product of A and B is A·B = 2(-1) + (-3)(0) + 0(5) = -2
Cosine of the angle between A and B is
cosθ = A·B / (|A||B|)
cosθ = -2 / (√13×√26)
cosθ = -2 / √(13×26)
Learn more about equation at
https://brainly.com/question/12998758
#SPJ11
If a=4, b=6, and sina=3/5 in triangle abc, then sin b eqauls
Answers
If a=4, b=6, and sina=3/5 in triangle abc, then sin b equals: 9/10
To find sin(b) in triangle ABC, we can use the sine function in a right angle and the given information.
Given:
a = 4
b = 6
sin(a) = 3/5
We know that the sine of an angle in a right triangle is equal to the ratio of the length of the side opposite the angle to the length of the hypotenuse.
In triangle ABC, let's label the side opposite angle a as side c and the hypotenuse as side h.
sin(a) = c / h
Substituting the given values:
3/5 = 4 / h
To solve for h, we can cross-multiply:
3h = 5 * 4
3h = 20
h = 20 / 3
Now, we can use the sine function to find sin(b):
sin(b) = side opposite angle b / hypotenuse
sin(b) = 6 / (20 / 3)
sin(b) = 6 * (3 / 20)
sin(b) = 18 / 20
sin(b) = 9 / 10
Therefore, sin(b) equals 9/10.
To know more about Sine function:
https://brainly.com/question/21902442
#SPJ11
Given the geometric sequence where a1 = 3 and the common ratio is −1, what is the domain for n?
Answers
Given the geometric sequence where a1 = 3 and the common ratio is −1, the domain for n is all integers where n ≥ 1.
What is geometric sequence?A geometric progression, sometimes referred to as a geometric sequence in mathematics, is a series of non-zero numbers where each term following the first is obtained by multiplying the preceding one by a constant, non-zero value known as the common ratio. For instance, the geometric progression 2, 6, 18, and 54 has a common ratio of 3. Similar to that, the geometric sequence 10, 5, 2.5, and 1.25 has a common ratio of 1/2.
A geometric sequence's behavior is determined by the common ratio's value.
The terms will all share the same sign as the first term, which is positive.
positive and negative phrases will be used alternately.
If the number is bigger than 1, exponential growth will continue until positive or negative infinity.
To learn more about geometric sequence from the given link:
https://brainly.com/question/11266123
#SPJ4
A 40 gram sample of a substance that’s used for drug research has a k-value of 0.1472.
Find the substance’s half-life, in days. Round your answer to the nearest tenth.
Answers
A 40 gram sample of a substance that’s used for drug research has a k-value of 0.1472. The substance's half-life, in days, is approximately 4.7 days.
The half-life of a substance is the time it takes for half of the substance to decay or undergo a transformation. The half-life can be determined using the formula:
t = (0.693 / k)
where t is the half-life and k is the decay constant.
In this case, we are given that the sample has a k-value of 0.1472. We can use this value to calculate the half-life.
t = (0.693 / 0.1472) ≈ 4.7 days
Therefore, the substance's half-life, rounded to the nearest tenth, is approximately 4.7 days.
For more such questions on k-value, click on:
https://brainly.com/question/1978047
#SPJ8
How do I solve these problems?

Answers
Answer:
1.) The 1ˢᵗ three term is (-32), (-7) and 18
2.) The 1ˢᵗ three term is 127, 106 and 85
Step-by-step explanation:
1.)Here,
First Term = a₁ = - 32
Common Difference = (d) = 25
Now, For 1ˢᵗ three term,
n = 1
a₁ = - 32
n = 2
aₙ = a + (n - 1)d
a₂ = (-32) + (2 - 1) × 25
a₂ = (-32) + 1 × 25
a₂ = (-32) + 25
a₂ = -7
n = 3
aₙ = a + (n - 1)d
a₃ = (-32) + (3 - 1) × 25
a₃ = (-32) + 2 × 25
a₃ = (-32) + 50
a₃ = 18
Thus, The 1ˢᵗ three term is (-32), (-7) and 18
2.)Here,
First Term = a₁ = 127
Common Difference = (d) = -21
Now, For 1ˢᵗ three term,
n = 1
a₁ = 127
n = 2
aₙ = a + (n - 1)d
a₂ = 127 + (2 - 1) × (-21)
a₂ = 127 + 1 × (-21)
a₂ = 127 - 21
a₂ = 106
n = 3
aₙ = a + (n - 1)d
a₃ = 127 + (3 - 1) × (-21)
a₃ = 127 + 2 × (-21)
a₃ = 127 - 42
a₃ = 85
Thus, The 1ˢᵗ three term is 127, 106 and 85
-TheUnknownScientist
In the figure below, m<1 = 39 degrees. find m<2, m<3 and m<4

Answers
TLDR; Angle 2= 141, Angle 3= 39, Angle 4= 141
The measure of angles are m ∠2 = 141°, m ∠3 = 39° and m ∠4 = 141°.
What are Angles?Angles are the figure formed by the intersection of two lines or rays by sharing a common point. This point is called the vertex of the angle.
Angles are usually measured in degrees or radians.
Vertical angles are opposite angles formed by two intersecting lines with a where the point of intersection is the common point for both of the angles.
Pairs of vertical angles are equal.
Here ∠1 and ∠3 are opposite angles.
∴ ∠1 = ∠3
Also ∠2 and ∠4 are vertical angles.
∴ ∠2 = ∠4
measure of ∠1 = 39°
So measure of ∠3 = 39°
Now ∠1 and ∠4 are supplementary, because they form a line.
∠1 + ∠4 = 180
39 + ∠4 = 180
∠4 = 180 - 39 = 141°
Since ∠2 = ∠4, we get ∠2 = 141°.
Hence the angle measures are m ∠2 = 141°, m ∠3 = 39° and m ∠4 = 141°.
Learn more about Angles here :
https://brainly.com/question/17039091
#SPJ2
What set of transformations could be applied to rectangle ABCD to create A″B″C″D″?
'Rectangle formed by ordered pairs A at negative 4, 2, B at negative 4, 1, C at negative 1, 1, D at negative 1, 2. The second rectangle is formed by ordered pairs A double prime at 2, negative 4, B double prime 1, negative 4, C double prime at 1, negative 1, D double prime at 2, negative 1.
A) Reflected over the x-axis and rotated 180°
B) Reflected over the y-axis and rotated 180°
C) Reflected over the x-axis and rotated 90° counterclockwise
D) Reflected over the y-axis and rotated 90° counterclockwise

Answers
Answer:
C) Reflected over the x-axis and rotated 90° counterclockwise
Step-by-step explanation:

Answer: Reflected over the x-axis and rotated 90° counterclockwise
Step-by-step explanation:
Took the test!
calculate the area of a rectangle when b= a and h = a +2. Use A= bh

Answers

in a certain population of fish, the lengths of the individual fish follow approximately a normal distribution with mean 54.0 mm and standard deviation 4.5 mm. we saw in example 4.3.1 that in this situation, 65.68% of the fish are between 51 and 60 mm long. suppose a random sample of four fish is chosen from the population. find the probability that
Answers
The probability that the average length of the four fish is between 51 and 60 mm is:
P(B) ≈ 0.658 .
Since the lengths of individual fish follow a normal distribution with mean 54.0 mm and standard deviation 4.5 mm, we can use the properties of the normal distribution to find the probabilities.
Let X be the length of a single fish. Then X follows a normal distribution with mean μ = 54.0 mm and standard deviation σ = 4.5 mm.
a) At least one fish in the sample is between 51 and 60 mm long:
Let A be the event that at least one fish in the sample is between 51 and 60 mm long. We want to find P(A).
The probability that a single fish is between 51 and 60 mm long is:
P(51 ≤ X ≤ 60) = P((51-54)/4.5 ≤ (X-54)/4.5 ≤ (60-54)/4.5) = P(-0.67 ≤ Z ≤ 1.11) ≈ 0.654
where Z is the standard normal variable.
Using the complement rule, the probability that none of the four fish are between 51 and 60 mm long is:
P(A') = P(no fish between 51 and 60 mm long) = (1 - 0.654)^4 ≈ 0.061
Therefore, the probability that at least one fish in the sample is between 51 and 60 mm long is:
P(A) = 1 - P(A') ≈ 0.939
b) The average length of the four fish is between 51 and 60 mm:
Let B be the event that the average length of the four fish is between 51 and 60 mm. We want to find P(B).
The distribution of the sample mean X is also normal with mean μ_X = μ = 54.0 mm and standard deviation σ_X = σ/√n = 4.5/√4 = 2.25 mm.
The probability that the average length of a sample of four fish is between 51 and 60 mm is:
P(51 ≤ X ≤ 60) = P((51-54)/(4.5/√4) ≤ (X -54)/(4.5/√4) ≤ (60-54)/(4.5/√4)) = P(-1.33 ≤ Z ≤ 0.89) ≈ 0.658
where Z is the standard normal variable.
Therefore, the probability that the average length of the four fish is between 51 and 60 mm is:
P(B) ≈ 0.658 .
Visit to know more about Probability:-
brainly.com/question/13604758
#SPJ11
Four point charges, each of magnitude 15.54μC, are placed at the corners of a square 82.6 cm on a side. If three of the charges are positive and one is negative, find the magnitude of the force experienced by the negative charge. The value of Coulomb's constant is 8.98755×10
9
N⋅m
2
/C
2
Answer in units of N.
Answers
The force experienced by the negative charge is -3.7431 N. The negative sign signifies that the force is attractive in nature.
Let the side of the square be a, therefore the distance between the charges on the diagonal would be d = a√2.
The electrostatic force on the negative charge due to the positive charges is calculated as given below:
F = kq1q2/d²... (1)
Since there are three positive charges, hence the total force on the negative charge would be:
Total Force = F1 + F2 + F3... (2) where F1, F2 and F3 are the force between the negative charge and the three positive charges.
Using equation (1) we get:
F1 = (8.98755 × 10⁹ × 15.54 × 10⁻⁶ × 15.54 × 10⁻⁶) / [(0.826 × √2)²]
F2 = F1 = F3 = (8.98755 × 10⁹ × 15.54 × 10⁻⁶ × 15.54 × 10⁻⁶) / (0.826)²
Using equation (2),
Total Force = 3
F1= 3 × (8.98755 × 10⁹ × 15.54 × 10⁻⁶ × 15.54 × 10⁻⁶) / [(0.826 × √2)²]
Putting the values of F1 and simplifying,Total Force = -3.7431 N
The force experienced by the negative charge is -3.7431 N. The negative sign signifies that the force is attractive in nature.
To know more about distance visit:
brainly.com/question/15172156
#SPJ11
What is the solution to the equation x - 12 = 36?x = 24x = 48x = 36x = -3
Answers
ANSWER :
x = 48
EXPLANATION :
From the problem, we have :
\(x-12=36\)add 12 to both sides :
\(\begin{gathered} x-12+12=36+12 \\ x=48 \end{gathered}\)The nth term of a number sequence is 7nFind the first three terms.
Answers
Answer:
7, 14, 21
Step-by-step explanation:
for n as term number
n = 1
7n = 7
n = 2
7n = 14
n = 3
7n = 21
hence the first 3 terms are 7, 14, 21
if an interior angle measures 120 degrees what is the measure of the adjacent exterior angle
Answers
Answer:
60
Step-by-step explanation:
180 - 120 = 60
when dealing with interior and exterior angles, the highest is 180 degrees
A bag contains 3 red and 5 green sweets.
Tim takes a sweet at random and eats it.
He then takes another sweet.
Find the probability that Tim takes 2 red sweets
Answers
Answer:
1/7
make sure to remember to remove a sweet when you take the second one, as it has been eaten.

Let f(x) = cx3 and Sx = [0, 2] (X is continuous).a. What value of c will make f(x) a valid density?
Answers
The value of c that makes f(x) a valid density function over [0, 2] is c = 1/4.
The function given to us is f(x) = cx, and we are asked to find the value of c that makes this a valid density function over the interval [0, 2]. To be a valid density function, a function must satisfy two properties:
The function must be non-negative over the interval.
The integral of the function over the interval must be equal to 1.
Let's first check the first property. For f(x) to be non-negative over the interval [0, 2], c must be non-negative as well. This is because x³ is always non-negative, and multiplying it by a negative value of c would make f(x) negative for some values of x.
So, we can conclude that c ≥ 0.
Now let's check the second property. We need to find the value of c that makes the integral of f(x) over [0, 2] equal to 1:
∫₀² cx³ dx = 1
We can solve this integral using the power rule of integration:
(c/4) [x⁴]₀² = 1
(c/4) (2⁴ - 0⁴) = 1
16c/4 = 1
4c = 1
c = 1/4
To know more about function here.
https://brainly.com/question/28193995
#SPJ4
