Answers
Answer:
left left right
Step-by-step explanation:
rearange the formula as normal
Related Questions
Write a definition for the function that best describes this graph.

Answers
Given the points on the graph:
(x, y) ==> (-1, 2), (0, 0), and (3, 1)
The graph represents a piece-wise function.
Let's write a definition for the function that best describes the graph.
Using the points, we have:
• (-1, 2) ==> f(x) = 2, when x = -1
,• (3, 1) ==> f(x) = 1, when x = 3
Let's find the equation of each line.
• Equation of line segment with endpoints (-1, 2) and (0, 0)
Apply the slope intercept form:
y = mx + b
Use the slope formula to find the slope:
\(\begin{gathered} m=\frac{y2-y1}{x2-x2} \\ \\ m=\frac{0-2}{0-(-1)}=\frac{-2}{1}=-2 \end{gathered}\)Therefore, the equation is:
y = -2x
• Equation of line segments with endpoints (3, 1) and (0, 0);
\(m=\frac{0-1}{0-3}=\frac{-1}{-3}=\frac{1}{3}\)Therefore, the equation is:
y = 1/3x
Hence, the definition for the functions that best describe the left piece of the graph is:
f(x) = -2x, if -1 ≤ x ≤ 0
The definition for the right piece of the function is:
f(x) = 1/3x, if 0 ≤ x ≤ 3
ANSWER:
f(x) = -2x, if -1 ≤ x ≤ 0
please im failing math and this is an extra credit problem.

Answers
Answer:
1:30 pm
Step-by-step explanation:
You want the time when Sahil catches up to Joaquin, who left at 8 am riding 50 mph when Sahil left at 8:30 am, riding at 55 mph.
Time, Speed, DistanceThe relation between time, speed, and distance is ...
distance = speed × time
time = distance / speed
Joaquin has a head start of 0.5 hours (30 minutes), during which time he traveled ...
head start distance = (50 mi/h) × (0.5 h) = 25 mi
Sahil is traveling 55 - 50 = 5 mph faster than Joaquin, so closes that gap at the rate of 5 mi/h. The time it takes to close the gap entirely is ...
time = distance / speed = 25 mi / (5 mi/h) = 5 h
So, 5 hours after Sahil starts at 8:30, the two riders will be at the same place.
Sahil catches Joaquin at 1:30 pm.
__
Additional comment
By the time the gap is closed at 1:30 pm, both riders will have traveled a distance of ...
distance = speed × time = 50 mi/h × 5.5 h = 55 mi/h × 5 h = 275 mi
In the attached graph, we have written equations for the total distance traveled by each motorcycle. The x-value used is the clock time on a 24-hour clock. That is, their meeting time of 13.5 hours corresponds to 13:30 hours or 1:30 p.m. on a 12-hour clock.

NEED ANSWER ASAP!!
How much water should be added to 18 mL of 15% alcohol solution to reduce the concentration to 9%?
Answers

what is answer to this question please help

Answers
Answer:
5 > \(\sqrt{18\)
Step-by-step explanation:
The square root of 18 is approximately 4.24.
5 is greater than 4.24, so we can use the inequality sign >.
I'm having trouble with this problem, if anyone could help I would really appreciate it. Thank you :)

Answers
The probability of the event of a wafer to be conforming and from lot A are as follows;
(a) P(A) ≈ 0.15541
(b) P(C) ≈ 0.84
(c) P(AC) ≈ 0.159
(d) P(A|C) ≈ 0.86
(e) P(C|A) ≈ 0.185
(f) E1 and E2 are independent events
How can the probability of an event be determined?Probability is given by the ratio of the number of required outcomes divided by the number of possible outcomes.
(a) The number of wafers from lot A = 79 + 13 = 92
79+13+157+43+260+40 = 592
Which gives;
The probability that the wafer is from lot A is therefore;
P(A) = 92/592 ≈ 0.15541(b) The conforming wafers = 79+157+260 = 496
Which gives;
P(C) = 496/592 ≈ 0.84(c) The conforming wafers in lot A are 79
Therefore;
The probability that the wafer is from lot A and conforming is therefore;
P(AC) = 79/496 ≈ 0.159(d) The probability that the wafer is conforming, given that it is from lot A is therefore;
P(A|C) = 79/92 ≈ 0.86
(e) The number of conforming wafers = 496
The probability that the wafer is from lot A given that it is conforming is therefore;
P(C|A) = 92/496 ≈ 0.185(f) Independent events are events such that the occurrence of one does not impact the probability of the other.
Given that the occurrence of E1 changes the probability of event E2 if the wafer is not replaced, the events are not independent events.
Learn more about dependent and independent events here:
https://brainly.com/question/488404
#SPJ1
An athlete runs 3 mi in 24 min. Is the rate of this athlete greater than, less than, or equal to the rate of an athlete who runs 4 mi in 33 min?
Answers
The rate of the first athlete is greater than the rate of the second athlete.
To determine if the rate of the first athlete is greater than, less than, or equal to the rate of the second athlete, we need to compare their average speeds.
The average speed of an athlete is calculated by dividing the distance traveled by the time taken.
For the first athlete who runs 3 miles in 24 minutes, the average speed can be calculated as:
Speed1 = Distance1 / Time1 = 3 miles / 24 minutes = 1/8 miles per minute.
For the second athlete who runs 4 miles in 33 minutes, the average speed can be calculated as:
Speed2 = Distance2 / Time2 = 4 miles / 33 minutes.
To make a comparison, we need to convert both rates to a common unit. Let's convert both rates to miles per minute:
Speed2 =\((4 miles / 33 minutes) * (24 minutes / 24 minutes)\) = (96 miles / 792 minutes) ≈ 0.1212 miles per minute.
Comparing the two rates, we see that Speed1 (1/8 miles per minute) is greater than Speed2 (0.1212 miles per minute). The rate of the first athlete is greater than the rate of the second athlete.
For more such questions on rate
https://brainly.com/question/119866
#SPJ8
What is the inequality in factored form that describes the set of values that is greater than the quadratic function with zeros –12 and 3 and includes the boundary point (–4.5, –450). y > 8(x – 3)(x + 12) y > 8(x + 3)(x – 12) y > –8(x + 3)(x – 12) y > –8(x – 3)(x + 12)
Answers
The inequality will be represented as y > 8(x – 3)(x + 12).
What is inequality?When two expressions are connected by a sign like "not equal to," "greater than," or "less than," it is said to be inequitable. The inequality shows the greater than and less than relation between variables and the numbers.
Expression in maths is defined as the collection of numbers variables and functions by using signs like addition, subtraction, multiplication and division.
Given that the inequality in a factored form describes the set of values that is greater than the quadratic function with zeros –12 and 3 and includes the boundary point (–4.5, –450).
The inequality will be written as below,
y > 8(x – 3)(x + 12).
To know more about inequality follow
https://brainly.com/question/24372553
#SPJ1
please help ! QUESTION 6
What is the acceleration of a runner who completes a 500 m sprint in 50 seconds? Initial velocity of the runner is 0 m/s and the runner is running in a straight line.
Options:
10 m/s²
0.2 m/s²
20 m/s^2
0.4m/s^2

Answers
The acceleration of the runner is 0.2 m/s².
We can use the following equation to get the runner's acceleration:
Acceleration (a) = (Final Velocity - Initial Velocity) / Time
In this case, the initial velocity (u) is 0 m/s, the final velocity (v) can be calculated using the formula:
v = s / t
where t is the amount of time spent and s is the distance travelled.
The time taken (t) and the distance travelled (s) are both provided as 500 m.
Calculate the b (v):
v = 500 m / 50 s
v = 10 m/s
Plug into the formula for acceleration:
a = (10 m/s - 0 m/s) / 50 s
a = 10 m/s / 50 s
a = 0.2 m/s²
Therefore, the acceleration of the runner is 0.2 m/s².
Learn more about acceleration click;
https://brainly.com/question/2303856
#SPJ1
the answer to the image included

Answers
Answer:
D
Step-by-step explanation:
Answer:19.3
Step-by-step explanation:add all angles of the shape that should give you 733
The minus 733 from 1080 because interior angles in a octagon add to 1080 this should give you 347 the add the the x together giving you 18x then divide 347 by 18 that give 19.27 rounded up to 19.3
Use the Remainder Theorem to evaluate f(10) for:
f(x) = 2x^3 – 14x^2 - 56x - 40
Answers
Step-by-step explanation:
Since we are told that 10 is a zero,
(x−10) must be a factor:
F(x)=2x3−14x2−56x−40
F(x)=(x−10) (2x2+6x+4)
F(x)=2(x−10)(x2+3x+2)
F(x)=2(x−10)(x+2)(x+1)
So the other two zeros are
x = -2 and x= −1
See image below for problem, thank you :))

Answers
Given: ∠XAM = ∠YBM = 90° and AM = BM
To prove: BX ≅ AY
Proof:
In the triangle XAM and BYM:
∠3 = ∠4 [vertically opposite angles]AM = BM [Given]∠XAM = ∠YBM [Both are 90°]From the ASA rule of congruency, we can say that: ΔXAM ≅ ΔYBM
Since ΔXAM ≅ ΔYBM: We can say that XM ≅ MY [CPCT - Common Part of Congruent triangles]
In the Triangle AMY and XMB:
∠1 = ∠2 [vertically opposite angles]AM = BM [Given]XM = MY [Proved above]From the SAS rule of congruency, we can say that: ΔAMY ≅ ΔXMB
Since ΔAMY ≅ ΔXMB: We can finally say that BX ≅ AY [CPCT]
Hence Proved!

Determine the equation of the circle with center (0, -2) containing the point
(√12,-5).
Answers
Answer:
i think its
x^2 + (y + 2)^2 = 21.
Step-by-step explanation:
The sum of three consecutive odd integers is 105.
What is the first integer?
Answers
Answer: how about 105/3 = 35, therefore the middle number is 35, and the 3 numbers are 33, 35, and 37.
Step-by-step explanation:
became Holy Roman Emperor in 1519
i know the answer but first person to answer gets brailyst
Answers
Answer:
Holy Roman Emperor, was the ruler and head of state of the holy Roman Empire.
The sum of the two numbers is 40. One number is 3 times the other number. Find the 2 numbers
Answers
Answer:
10 and 30
Step-by-step explanation:
The sum of 10 and 30 is 40.
30 is three times ten (10 x 3 = 30).
hope this helps!
The answer is 10 and 30
10 times 3 is 30, meaning 10 will be the number times 3 they wanted. 10 + 30 is 40, therefore the answer is 10 and 30
Please open the image and help me

Answers
1.
Looks like
\(y=2\sqrt[3]{x}+\dfrac1{x^2}+\pi\)
Write \(\sqrt[3]{x}\) as a fractional power, \(x^{1/3}\). This makes it more obvious that the power rule should be used here.
\(y'=(2x^{1/3})'+(x^{-2})'+\pi'\)
\(y'=\dfrac23x^{-2/3}-2x^{-3}\)
\(y'=\dfrac2{3\sqrt[3]{x^2}}-\dfrac2{x^3}\)
2.
\(y=(\sin(2x)+\tan(3x))^e\)
Power and chain rule:
\(y'=\left((\sin(2x)+\tan(3x))^e\right)'\)
\(y'=e(\sin(2x)+\tan(3x))^{e-1}(\sin(2x)+\tan(3x))'\)
\(y'=e(\sin(2x)+\tan(3x))^{e-1}(\cos(2x)(2x)'+\sec^2(3x)(3x)')\)
\(y'=e(\sin(2x)+\tan(3x))^{e-1}(2\cos(2x)+3\sec^2(3x))\)
Brian set his compass equal to the radius of circle C and drew two circles centered at points A and B on circle C. He labeled the points of intersection of the two circles as shown.
Two circles are drawn by having another circle in the center. The center circle has points A, M, N, B, P, Q, and C. At C the two circles intersect, and at P the center circle and the top circle intersect.
To complete his construction, Brian only needs to use his straightedge to draw some chords of circle C.
Which figures could Brian be constructing?
equilateral triangle MNQ inscribed in circle C
equilateral triangle ANP inscribed in circle C
regular hexagon AMNBPQ inscribed in circle C
square MNPQ inscribed in circle C
square ANBQ inscribed in circle C
Answers
The correct options that could be constructed by Brian using his straightedge to draw some chords of circle C are:
Equilateral triangle MNQ inscribed in circle C
Regular hexagon AMNBPQ inscribed in circle C
Brian is constructing figures inscribed in circle C.
Equilateral triangle MNQ inscribed in circle C:
This option is possible since the points M, N, and Q are labeled and they lie on circle C.
Equilateral triangle ANP inscribed in circle C:
This option is not possible. The points A and P are labeled, but the third vertex of the equilateral triangle is not specified.
Regular hexagon AMNBPQ inscribed in circle C:
This option is possible since the points A, M, N, B, P, and Q are labeled and they lie on circle C.
Square MNPQ inscribed in circle C:
This option is not possible based on the given information. The label points do not form a square.
Square ANBQ inscribed in circle C:
This option is not possible . The points A, N, B, and Q are labeled, but they do not form a square.
The correct options that could be constructed by Brian using his straightedge to draw some chords of circle C are:
Equilateral triangle MNQ inscribed in circle C
Regular hexagon AMNBPQ inscribed in circle C
For more questions on circle
https://brainly.com/question/28162977
#SPJ8
Penny is training for a race. First she ran 1/10 of a mile 4 times. Next she ran 1/5 of a mile 3 times. Then she ran 3/10 of a mile 2 times. How far did Penny run during her training?
Answers
Answer:
4/10 + 6/10 + 6/10 = 16/10 = 1 6/10
Step-by-step explanation:
Complete the tasks to subtract the polynomials vertically.
(1.3t3 + 0.4t2 – 24t) – (0.6t2 + 8 – 18t)
What is the additive inverse of the polynomial being subtracted?
Answers
The additive inverse of the polynomial is A' = - ( 1.3t³ - 0.2t² - 6t - 8 )
Given data ,
Let the polynomial be represented as A
Now , the value of A is
A = ( 1.3t³ + 0.4t² - 24t ) - ( 0.6t² + 8 - 18t )
On simplifying the equation , we get
A = 1.3t³ + 0.4t² - 24t - 0.6t² - 8 + 18t
A = 1.3t³ - 0.2t² - 6t - 8
Now , the additive inverse of the polynomial is
A' = - ( 1.3t³ - 0.2t² - 6t - 8 )
Hence , the polynomial is solved
To learn more about polynomial equations click :
https://brainly.com/question/13199883
#SPJ1
What is the slope of the line through? (-4, 2) and (3, -3)?

Answers
Answer:
c. -5/7
Step-by-step explanation:
The question is below thanks

Answers
Answer:
AC = 49
Step-by-step explanation:
Using the Altitude - on - Hypotenuse theorem
(leg of large Δ )² = (part of hypotenuse below it ) × (whole hypotenuse)
BC² = DC × AC, substitute values
14² = 4 × x
196 = 4x ( divide both sides by 4 )
49 = x
Thus AC = x = 49
Step-by-step explanation:
pythogoream theorem.(hyp^2=opp^2+adj^2)
hyp=14 adg=4 opp=?
since we have to find opp
opp^2=hyp^2-adj^2
opp^2=14^2-4^2
196-16=180
\( \sqrt{180} \)
BD= 13.41
(Q as theta)
sinQ= opp÷hyp
= 13.41÷14
Q=sin^-1(13.4÷14)
Q=73.33
cosQ=adj(AD)÷hyp(BC)
cos 73.33× 14 =adj
AD=4.01
Therefore, AC =AD +DC(4.01+4)
=8.01
I am not sure....but I got this much
In a sample of n = 6 scores, 5 of the scores are each above the mean by one point. Where is the 6th score located relative to the mean?
Answers
The mean of a dataset is the sum of all data elements divided by the count of the elements.
The location of the 6th score relative to the mean is 5 points below the mean
Let:
\(\bar x \to\) Mean
\(a \to\) 5 scores
\(b \to\) 6th scores
Given that:
\(n = 6\)
The 5 scores that are 1 above the mean implies that:
\(a = \bar x + 1\)
The mean of a dataset is calculated using:
\(\bar x = \frac{\sum x}{n}\)
So, we have:
\(\bar x =\frac{5a + b}{6}\)
\(\bar x =\frac{5(\bar x + 1) + b}{6}\)
Open brackets
\(\bar x =\frac{5\bar x + 5 + b}{6}\)
Multiply both sides by 6
\(6\bar x =5\bar x + 5 + b\)
Make b the subject
\(b = 6\bar x -5\bar x - 5\)
\(b = \bar x - 5\)
This means that the 6th score is 5 points below the mean
Read more about mean at:
https://brainly.com/question/17060266
there are 84 players on a football team. the ratio of offensive players to the defense is 4 to 3. how many offensive players are on the team?
Answers
84/7=12
12x4=48
12x3=36
48 players on offensive team
Polygon ABCD was transformed in polygon A'B'C'D. Identify the sequence of transformations performed. Select all that applied
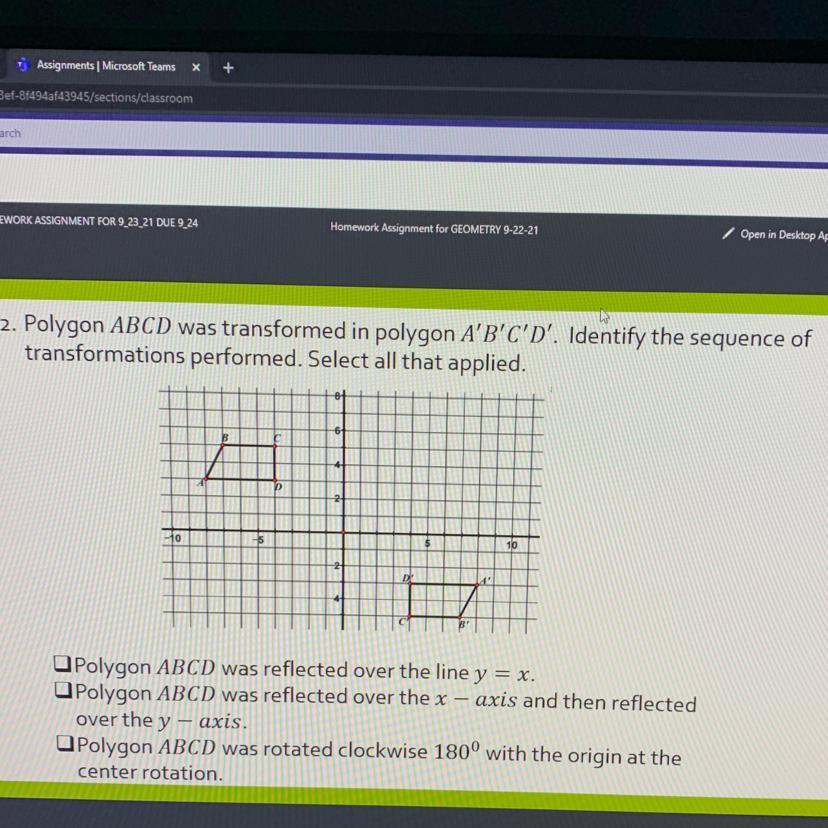
Answers
Answer:
B. Polygon ABCD was reflected over the x-axis and then reflected over the y-axis.
What is the equation in point slope form of the line that is perpendicular to the given line and passes through the point(2,5)?
Answers
Answer:
Step-by-step explanation:
To find the equation of a line that is perpendicular to a given line and passes through a specific point, we need to follow a few steps:
Find the slope of the provided line.
The point-slope form of a line is given by: y - y1 = m(x - x1), where (x1, y1) represents the given point.
Substituting the values, the equation of the perpendicular line becomes:
y - 5 = (-1/m)(x - 2)
Simplifying the equation further, we can rewrite it in point-slope form:
y - 5 = (-1/m)x + (2/m)
Ayuda operaciones y respuesta es para ahora

Answers
The perimeter of the given window is 48 centimeter.
From the given figure,
Perimeter of window = 2(Length+Breadth)
= 2(10+14)
= 2×24
= 48 centimeter
Perimeter of house = 2(Length+Breadth)
= 2(37+35)
= 2×72
= 144 centimeter
Perimeter of roof = 2(Length+Breadth)
= 2(37+5)
= 2×42
= 84 centimeter
Therefore, the perimeter of the given window is 48 centimeter.
To learn more about the perimeter visit:
https://brainly.com/question/6465134.
#SPJ1
Whole page of geometry stuff for 50 points only do 2,3 and 4 ( serious answers only or 1 star and report )

Answers
See below for the distance between the points and the lines
How to determine the distance between the lines and the points?Question 2
The line and the points are given as:
x = y
P = (4, -2)
Rewrite the equation as:
y = x
The slope of the above equation is
m = 1
The slope of a line perpendicular to it is
m = -1
A linear equation is represented as:
y = mx + b
Substitute m = -1
y = -x + b
Substitute (4, -2) in y = -x + b
-2 = -4 + b
Solve for b
b = 2
Substitute b = 2 in y = -x + b
y = -x + 2
So, we have:
x = y and y = -x + 2
Substitute x for y
x = -x + 2
Solve for x
x = 1
Substitute x = 1 in y = x
y = 1
So, we have the following points
(1, 1) and (4, -2)
The distance between the above points is
d = √(x2 - x1)² + (y2 - y1)²
So, we have:
d = √(1 - 4)² + (1 + 2)²
Evaluate
d = 3√2
Hence, the distance between x = y and P = (4, -2) is 3√2 units
Question 3
The line and the points are given as:
y = 2x + 1
Q = (2, 10)
The slope of the above equation is
m = 2
The slope of a line perpendicular to it is
m = -1/2
A linear equation is represented as:
y = mx + b
Substitute m = -1/2
y = -1/2x + b
Substitute (2, 10) in y = -1/2x + b
10 = -1/2 * 2 + b
Solve for b
b = 11
Substitute b = 11 in y = -1/2x + b
y = -1/2x + 11
So, we have:
y = 2x + 1 and y = -1/2x + 11
Substitute 2x + 1 for y
2x + 1 = -1/2x + 11
Solve for x
x = 4
Substitute x = 4 in y = 2x + 1
y = 9
So, we have the following points
(4, 9) and (2, 10)
The distance between the above points is
d = √(x2 - x1)² + (y2 - y1)²
So, we have:
d = √(4 - 2)² + (9 - 10)²
Evaluate
d = √5
Hence, the distance between the line and the point is √5 units
Question 4
The line and the points are given as:
y = -x + 3
R = (-5, 0)
The slope of the above equation is
m = -1
The slope of a line perpendicular to it is
m = 1
A linear equation is represented as:
y = mx + b
Substitute m = 1
y = x + b
Substitute (-5, 0) in y = x + b
0 = 5 + b
Solve for b
b = -5
Substitute b = 5 in y = x + b
y = x + 5
So, we have:
y = x + 5 and y = -x + 3
Substitute x + 5 for y
x + 5 = -x + 3
Solve for x
x = -1
Substitute x = -1 in y = x + 3
y = 2
So, we have the following points
(-1, 2) and (-5, 0)
The distance between the above points is
d = √(x2 - x1)² + (y2 - y1)²
So, we have:
d = √(-1 + 5)² + (2 - 0)²
Evaluate
d = 2√5
Hence, the distance between the line and the point is 2√5 units
Read more about distance at:
https://brainly.com/question/7243416
#SPJ1
For the following vectors, (a) find the dot product v•w ; (b) find the angle between v and w , (c) state whether the vectors are parallel, octagonal, or neither. V=-3i-4j, w=6i+8j
A- v•w
B-the angle between v and w is theta ^•?
C- the vectors v and w are?
Answers
B) The angle between vectors v and w can be found using the formula: cos(theta) = (v • w) / (||v|| ||w||), where ||v|| and ||w|| are the magnitudes of vectors v and w respectively.
First, we need to find ||v|| and ||w||:
||v|| = sqrt((-3)^2 + (-4)^2) = 5
||w|| = sqrt((6)^2 + (8)^2) = 10
Now, we can substitute in the values to get:
cos(theta) = (-50) / (5 * 10) = -1
theta = arccos(-1) = pi radians or 180 degrees.
Therefore, the angle between vectors v and w is 180 degrees.
C) Two vectors are parallel if their directions are the same, which can be determined by comparing their unit vectors.
The unit vector of v is:
v_hat = v / ||v|| = (-3/5)i + (-4/5)j
The unit vector of w is:
w_hat = w / ||w|| = (6/10)i + (8/10)j = (3/5)i + (4/5)j
We can see that the unit vectors are in opposite directions, which means that the vectors are anti-parallel or opposite. Therefore, the vectors v and w are neither parallel nor orthogonal.
HELPIn order to find the percentage of households in a town that own more than one vehicle, a survey asks 1000 randomly selected drivers at a
gas station how many vehicles are owned in their household. From the results of the survey, it is reported that 67% of households in the town
have more than one vehicle.
Why is this report biased?
Answers
Answer:
This report is biased because most people drive to gas stations.
Step-by-step explanation:
The distance to a gas station is often further than walking distance. Therefore, most people will take a car because it's quicker, and most people go to gas stations to get gas.
Let X1, X2,..,X100 be a random sample from a distribution with pdf f(x) = {x2 +Źosxs1 (0, otherwise Find the standard deviation of (round off to second decimal place).
Answers
The standard deviation of the sample is 0.63
What is standard deviation?
A random variable, sample, statistical population, data set, or probability distribution's standard deviation is equal to the square root of its variance.
To find the standard deviation of the sample, we need to first find the mean of the distribution. The mean of a distribution is given by the expected value of the random variable, which can be calculated as follows:
\(E[X] = \int\limits {xf(x)dx}\)
Substituting the given pdf for f(x), we get:
\(E[X] = \int\limits {x(x2 + Źosxs1)dx}\)
Evaluating the integral, we get:
\(E[X] = (x3/3) + (Źosxs2/2) |0\\\\ E[X] = (1/3) + (0/2)\\\\ E[X] = 1/3\)
Next, we need to find the variance of the distribution. The variance of a distribution is given by the expected value of the squared deviation of the random variable from its mean, which can be calculated as follows:
\(Var[X] = E[(X - E[X])2]\)
Substituting the value of E[X] that we just found, we get:
Var[X] = E[(X - (1/3))2]
Var[X] = ∫((x - (1/3))2)(x2 + Źosxs1)dx
Evaluating the integral, we get:
Var[X] = ((x - (1/3))2)(x2 + Źosxs1) |0
Var[X] = ((1 - (1/3))2)(1 + 0) - ((0 - (1/3))2)(0 + 0)
Var[X] = (4/9)(1) - (1/9)(0)
Var[X] = 4/9
Finally, the standard deviation of the distribution is the square root of the variance, which is:
\(Std\ Dev[X] = \sqrt{Var[X]}\\\\ Std\ Dev[X] = \sqrt{(4/9) } \\\\Std\ Dev[X] = 0.63\)
Rounding off to the second decimal place, the standard deviation of the sample is 0.63.
Hence, The standard deviation of the sample is 0.63
To know more about standard deviation visit,
https://brainly.com/question/475676
#SPJ4
