Elon is paid by the hour. He earned $50 for a 4 hour workday. How much
does he earn in one hour?
Answers
Answer:
$12.50 per hour
Step-by-step explanation:
Elon is paid by the hour. He earned $50 for a 4 hour workday. How much does he earn in one hour?
50 / 4 = $12.50 per hour
Related Questions
1. NASA wants to appoint 2 men and 3 women to send back to the moon in 2018. The finalists for these positions consist of 6 men and 8 women. In how many ways can NASA make this selection?2.Melissa, Anna, Chris, Nora, and Wade are attending a play. If Melissa and Wade want to sit together, in how many ways can we seat them in five seats? (Hint: It may be helpful to draw a diagram to get you started)
Answers
There are 840 ways for NASA to make this selection. Total number of ways melissa and wade can sit together is 96.
We can use the combination formula to solve this problem. The number of ways to choose 2 men from 6 is C(6,2) = 15, and the number of ways to choose 3 women from 8 is C(8,3) = 56. To find the total number of ways to make the selection, we multiply these values together: 15 x 56 = 840.
To solve this problem, we can treat Melissa and Wade as a single unit and then arrange the other 3 people and the Melissa-Wade unit in 4 seats. There are 4 ways to arrange Melissa and Wade (MW, WM, AMW, WMA). After that, we have 4 seats left, and we need to arrange 3 people (Anna, Chris, and Nora) and the Melissa-Wade unit in those seats. There are 4 people to arrange in 4 seats, so there are 4! = 24 ways to do this. Therefore, the total number of ways to seat Melissa and Wade together is 4 x 24 = 96.
Learn more about combinations here: brainly.com/question/11732255
#SPJ4
Give the angle measure.
M/E, given PQR= DEF, M/R=13 and M/D=62

Answers
Answer:
From the given information the answer should be m angle e= 105 degrees.
Step-by-step explanation: Well you have triangle PQR equal to triangle DEF. That means it has the same angle measurement as well as side measurement. You would add 13 and 62 to sum to 75. Then we know triangles equal 180 degrees. Then subtract 75 from 180 to get 105 degrees.
Consider the polygon GEOM with coordinate G(0 -2) E(-12), O(-5, 1), M(-5,-6). If we rotate GEOM 90° clockwise about the origin, then reflect over the y-axis, what are the coordinate of G"E"O"M ?
Answers
I need a answer on this math equation
4 + (−1 2/3)
Any solutions?
Answers
there are 500 students in tim's high school. 40% of the students are taking spanish. how many students are taking spanish?
Answers
Answer:
200 students
--------------------
40% out of 500 students taking Spanish.
Find it in number:
40/100 * 500 = 40*5 =200
Find the first derivative for each of the following:
y = 3x2 + 5x + 10
y = 100200x + 7x
y = ln(9x4)
Answers
The first derivatives for the given functions are:
For \(y = 3x^2 + 5x + 10,\) the first derivative is dy/dx = 6x + 5.
For \(y = 100200x + 7x,\) the first derivative is dy/dx = 100207.
For \(y = ln(9x^4),\) the first derivative is dy/dx = 4/x.
To find the first derivative for each of the given functions, we'll use the power rule, constant rule, and chain rule as needed.
For the function\(y = 3x^2 + 5x + 10:\)
Taking the derivative term by term:
\(d/dx (3x^2) = 6x\)
d/dx (5x) = 5
d/dx (10) = 0
Therefore, the first derivative is:
dy/dx = 6x + 5
For the function y = 100200x + 7x:
Taking the derivative term by term:
d/dx (100200x) = 100200
d/dx (7x) = 7
Therefore, the first derivative is:
dy/dx = 100200 + 7 = 100207
For the function \(y = ln(9x^4):\)
Using the chain rule, the derivative of ln(u) is du/dx divided by u:
dy/dx = (1/u) \(\times\) du/dx
Let's differentiate the function using the chain rule:
\(u = 9x^4\)
\(du/dx = d/dx (9x^4) = 36x^3\)
Now, substitute the values back into the derivative formula:
\(dy/dx = (1/u) \times du/dx = (1/(9x^4)) \times (36x^3) = 36x^3 / (9x^4) = 4/x\)
Therefore, the first derivative is:
dy/dx = 4/x
To summarize:
For \(y = 3x^2 + 5x + 10,\) the first derivative is dy/dx = 6x + 5.
For y = 100200x + 7x, the first derivative is dy/dx = 100207.
For\(y = ln(9x^4),\) the first derivative is dy/dx = 4/x.
For similar question on derivatives.
https://brainly.com/question/31399608
#SPJ8
Each grid square is 1 square unit. Find the area, in square units, of the shape without counting every square. Be prepared to explain your reasoning.

Answers
The total area of the two rectangles is given by the equation A = 33 units²
What is the Area of a Rectangle?The area of the rectangle is given by the product of the length of the rectangle and the width of the rectangle
Area of Rectangle = Length x Width
Given data ,
Let the total area of the 2 rectangles be A
Now , each grid square represents = 1 square unit
Now , let the first rectangle be represented as P
The length of P = 4 grid squares
The width of P = 3 grid squares
Let the second rectangle be represented as Q
The length of Q = 7 grid squares
The width of Q = 3 grid squares
So , Area of Rectangle = Length x Width
The area of rectangle P = 4 x 3
The area of rectangle P = 12 units²
The area of rectangle Q = 7 x 3
The area of rectangle Q = 21 units²
So , the total area of figure A = area of P + area of Q
On simplifying the equation , we get
Total area of figure A = 12 units² + 21 units²
Total area of figure A = 33 units²
Therefore , the value of A is 33 units²
Hence , the area is 33 units²
To learn more about area of rectangle click :
https://brainly.com/question/15225905
#SPJ1
Use the equation y+5=x/4 to fill in the missing values in the table below

Answers
We have to find the missing values of the table by substituting the input or output values in the given equation,
y + 5 = \(\frac{x}{4}\)Here, y = output values of the function
x = input values
For x = 12,
y + 5 = \(\frac{12}{4}\)
y = 3 - 5
y = -2
For x = 0,
y + 5 = \(\frac{0}{4}\)
y = 0 - 5
y = -5
For y = 0,
0 + 5 = \(\frac{x}{4}\)
x = -5×4
x = -20
For y = -8,
-8 + 5 = \(\frac{x}{4}\)
x = -3×4
x = -12
Learn more,
https://brainly.com/question/17654974
Plsssssssssss help me!!! I’m not good at algebra!!
What is the value of x?
The screenshot is down below.

Answers
Answer:
x=50
Step-by-step explanation:
This is a vertical angle, so the angle on top and the bottom are equal
[2(x+10)]=3x-30
2(x+10)=3x-30
2x+20=3x-30
50=x
Solve the following formula for the indicated variable.P = a + b + c; solve for b
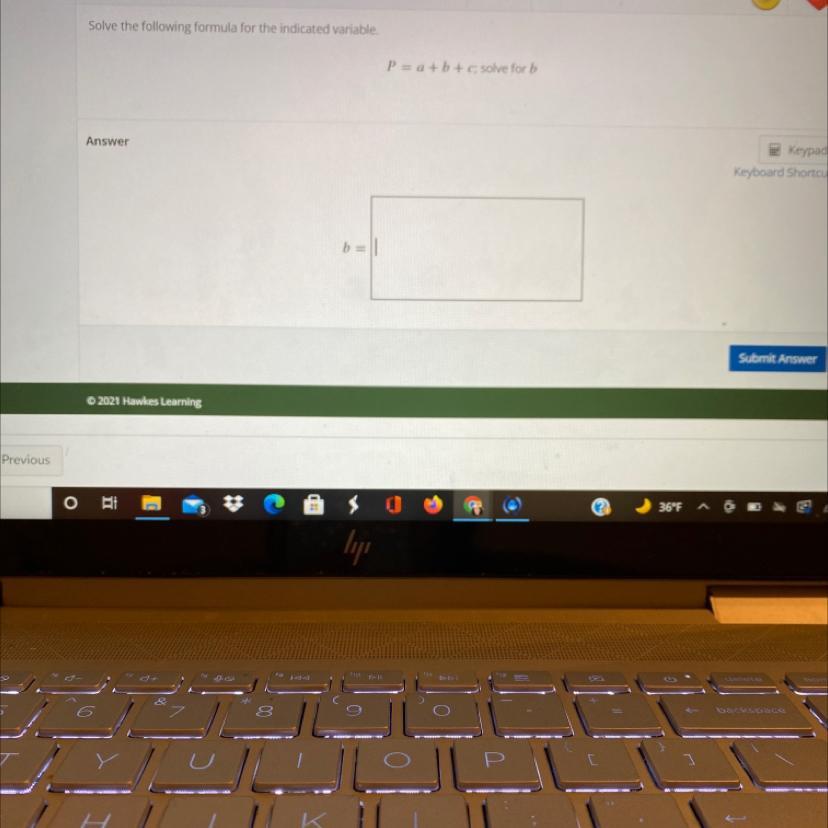
Answers
SOLUTION:
Step 1:
In this question, we are given the following:
Step 2:
Now, we are given the following:
\(\text{P = a+b + c}\)We are to solve for b, which means that we are to make b the subject of the formulae:
Step 3:
Now, solving for b, we have that:
\(b\text{ = P - a - c}\)h

Find the slope of the line that contains (10,-1) and (-8,6)
Answers
Answer:
the slope of the line that passes throught (x1,y1) and (x2,y2) is (y2-y1)/(x2-x1)
given
(-4,3) and (-8,6)
slop=(6-3)/(-8-(-4))=(3)/(-8+4)=3/-4=-3/4
slope is -3/4
Step-by-step explanation:
Answer:
(y2-y1)/(x2-x1)
(6+1)/ (-8-10)
7/ -18 is the slope
Step-by-step explanation:
Write an English phrase that would translate into the following mathematical expression.
5z -7
Which of the following is equivalent to the expression 5z-7?
A. The quotient of 5 times a number z and 7
B. 7 less than the product of 5 and a number z
C. 5 less than the product of 7 and a number z
D. 5 times the difference of a number z and 7

Answers
Answer:
C.
Step-by-step explanation:
5z - 7, you would say 5 times z minus 7, which is the same as 5 less than th product of 7 and a number z
Divide £150 in the ratio 1:4
Answers
Step-by-step explanation:
Hey there!
Given ratio is= 1:4
Let "X" be the common factor. So,
x+ 4x = £150
5x = £150
X = £150/5
X = £30
OR ;
1:4 = 1*30 : 4*30
Therefore, the answer is 30:120.
Hope it helps...
Answer:
30:120
Step-by-step explanation:
1+4=5
150 divide 5=30
30x1=30
30x4=120
30:120
If p(x)=(3x+2)(2x−3), what are the zeros of the polynomial?
x=-23 and x=32
x=23 and x=-32
x=-2 and x=3
x=2 and x=-3
Answers
Answer:
Option A is the correct answer. ; x=-2/3 and x=3/2
Step-by-step explanation:
We have been given that p(x)=(3x+2)(2x−3) is a polynomial.
According to the question's statement, Question asks us to find the zeros of the polynomial.
Let's head to the question in order to get required answer.
p(x)=(3x+2)(2x−3)
=> p(x) = 3x(2x-3) + 2(2x-3)
=> p(x) = 6x² - 9x + 4x - 6
=> p(x) = 6x² - 5x - 6 (This is the standard form for the given polynomial)
Now, We need to find the zeros of the polynomial. So, In order to find its zeros, we need to put p(x).
p(x) = (3x+2)(2x-3)
=> 0 = (3x+2)(2x-3)
=> (3x+2) = 0 or (2x-3) = 0
=> x= -2/3 or x = 3/2
Hence, If p(x)=(3x+2)(2x−3), x = -2/3 & x= 3/2 are the zeros of the polynomial.
What is x?
Please help!!!

Answers
Answer:
Below
Step-by-step explanation:
For RIGHT triangles
Cos (21°) = adjacent leg / hypotenuse
cos ( 21°) = x / 21
re-arrange to
21 * cos (21°) = x then use calculator to find x = 19.6 units
( it may not look like it from the picture...but the picture is not drawn to scale : a 21° angle is much smaller than pictured)
What is 15/20 simplest form
Answers
Answer:
the simplest form of 15/20 is 3/4
how many cup sugar in g?
Answers
As a rough estimate, 100g of sugar is equivalent to 0.5 cups of granulated sugar.
Conversion is the process of changing units of measurement from one system to another.
In this case, we need to convert 100g of sugar into cups. However, the conversion factor for sugar varies depending on factors such as the type of sugar and how densely it is packed. For instance, powdered sugar is denser than granulated sugar, and so the conversion factor will differ.
In general, one cup of granulated sugar weighs around 200g, which means that 100g of sugar is equivalent to 0.5 cups. However, it is essential to note that this conversion factor is approximate and can vary depending on the quality and type of sugar used.
To know more about measurement here.
https://brainly.com/question/4725561
#SPJ4
Complete Question:
how many cup sugar in 100g?
(y-4)6
help please....
Answers
6(y) =6y
4(6)= 24
Suppose that the rational preference relation is continuous and monotone. Then there is a continuous utility function that represents the rational preference relation. Prove it with the help of a diagram for 2 commodity framework.
Answers
Yes, there is a continuous utility function that represents a rational preference relation when it is both continuous and monotone.
In a two-commodity framework, let's assume the two commodities are represented by X and Y. We can construct a diagram with the axes representing the quantities of X and Y. The indifference curves, which represent the bundles of X and Y that yield the same level of utility, can be plotted on this diagram.
Since the preference relation is continuous and monotone, we can draw the indifference curves as smooth, upward-sloping curves without any gaps or jumps. The upward slope reflects the monotonicity, indicating that more of either X or Y is preferred to less.
To represent this preference relation with a continuous utility function, we can assign utility levels to different bundles of X and Y. For example, we can assign a utility level of 1 to a specific bundle (X₁, Y₁), and higher utility levels to bundles that are preferred to (X₁, Y₁).
By assigning utility levels in a continuous manner across the diagram, we can construct a continuous utility function that represents the rational preference relation. This function will map each bundle of X and Y to a corresponding level of utility.
In conclusion, for a rational preference relation that is continuous and monotone in a two-commodity framework, there exists a continuous utility function that represents this preference relation. The utility function can be constructed by assigning utility levels to different bundles of commodities, and the resulting indifference curves on a diagram will be smooth, upward-sloping curves. This relationship between the utility function and the preference relation allows us to mathematically model and analyze the choices and preferences of individuals in economics.
To know more about continuous utility function, visit;
https://brainly.com/question/28593010
#SPJ11
Use the formula to find the volume of the figure. Show your work.

Answers
Hello !
Answer:
\(\boxed{\sf V{cone} \approx 2408.55 m^3}\)
Step-by-step explanation:
To find the volume of a cone with the radius of its base and its height, we will apply the following formula:
\( \sf V{cone} = \dfrac{\pi \times r^2 \times h}{3} \)
Where r is the radius of its base and h is its height.
Given:
r = 10 mh = 23 mLet's substitute our values into the formula:
\(\sf V{cone} = \dfrac{\pi (10)^2(23)}{3} = \dfrac{2300\pi}{3} \ \ \\\boxed{\sf V{cone} \approx 2408.55 m^3}\)
Have a nice day ;)
log3(5x+1)=4 A.) x = 5 B.) x = 16 C.) x = 4 D.) x = 3
Answers
Answer:
B) x=16
Step-by-step explanation:
The 3 is the base, the expression in the parenthesis is the argument and the 4 is the exponent
We also know that \(base^{exponent}\) = argument
so therefore the new equation is \(3^{4}\) = 5x+1
3 to the fourth power is 81
so 81=5x+1
then solve algebraically
heyy everyone a little halp here i kinda need it fast sorry
The heights of Rahul, Akash, Meera and Lakshmi are 1.54m, 1500mm,
152cm,1560mm respectively.
a) Arrange their heights in ascending order.
b) Who is the tallest among them?
Answers
Answer:
A) Akash (1.5m), Meera (1.52), Rahul (1.54m), Lakshmi (1.56m)
B) Lakshmi is the tallest, 1.56m tall
Step-by-step explanation:
Rahul- 1.54m
Akash- 1500mm
Meera- 152cm
Lakshmi- 1560mm
Let's start by converting all the measurements to meters.
Rahul is already in meters, so he can just stay the same.
1500mm = 1.5m
152cm = 1.52m
1560mm = 1.56m
So our new measurements are:
Rahul- 1.54m
Akash- 1.5m
Meera= 1.52m
Lakshmi= 1.56m
We can now make our conclusions.
A) Akash (1.5m), Meera (1.52), Rahul (1.54m), Lakshmi (1.56m)
B) Lakshmi is the tallest, 1.56m tall
Answer:
Step-by-step explanation:
Let's convert all the heights to meters:
Rahul 1.54m
Akash 1.50 m
Meera 1.52 m
Lakshmi 1.56m
Now, let's arrange their heights in ascending order (shortest to tallest):
Akash 1.50 m
Meera 1.52 m
Rahul 1.54m
Lakshmi 1.56m
a) 1500 mm, 152 cm, 1.54 m, 1560 mm
b) therefore Lakshmi is the tallest.
PLEASE HELP ME!
A population grows according to an exponential growth model. The initial population is 9, and the grows by 8% each year.
Find an explicit formula for the population growth. Use that formula to evaluate the population after 9 years.
Round your answer to two decimal places
Answers
The explicit formula for the population growth is P(t) = 9 * (1 + 0.08)^t, where P(t) represents the population at time t, P0 is the initial population of 9, r is the growth rate of 8% or 0.08, and t is the time in years. Using this formula, we can calculate the population after 9 years which is approximately 16.03
To find the explicit formula for the population growth, we use the exponential growth model formula P(t) = P0 * (1 + r)^t. In this case, P0 is given as 9, and the growth rate r is 8%, or 0.08 when expressed as a decimal. Plugging these values into the formula, we get P(t) = 9 * (1 + 0.08)^t.
To evaluate the population after 9 years, we substitute t = 9 into the formula and calculate: P(9) = 9 * (1 + 0.08)^9. Using a calculator or performing the calculation manually, the population after 9 years is approximately 16.03 (rounded to two decimal places).
Therefore, the population after 9 years, based on the exponential growth model with an initial population of 9 and a growth rate of 8%, is approximately 16.03
To learn more about population growth, click here: brainly.com/question/29885709
#SPJ11
Which data set is the most spread from its mean?
14, 26, 24, 28
O22, 16, 18, 36
O22, 28, 20, 22
O 21, 19, 27, 25
Answers
Option B (22,16,18,36)
Mean- Mean is an average of the data collected in the data set. It can be found by dividing the sum of the values by the number of values. Median is the middle value of the data set when the values are placed in order from least to greatest.
It is easy to calculate: add up all the numbers, then divide by how many numbers there are.
Add all the numbers (22+16+18+36) = 92
Avarage = sum of the all given numbers/ total numbers
total numbers =4
so avarage= mean= 92/4 =23
(22,16,18,36) has the most spread because one number as low as 16 and one as high as 36. Our mean is 23, so that means that the spread is huge.
Hence the answer is (22,16,18,36).
For more information about Mean
visit : brainly.com/question/1635504
#SPJ9
I need help, Whats 9+10=
Answers
Answer:
19
Step-by-step explanation:
Answer:
the answer is 19
Step-by-step explanation:
you have 9 things then you added then you will get 19
Delaney is saving money in an account that offers 9% simple interest. She deposits 2000 from her grandmother into the account and makes no additional deposits or withdraws. How many years will it take to grow to 4,700
Answers
Answer:
15years
Step-by-step explanation:
Given data
Rate= 9%
Principal= $2000
Final amount= $4700
The simple interest formula is given as
A= P(1+rt)
Substitute
4700=2000(1+0.09*t)
4700= 2000+ 180t
4700-2000= 180t
2700=180t
t= 2700/180
t= 15 years
Hence the time is 15years
Find the percent increase. Round to the nearest percent.
From 96 books to 127 books
The percent increase is
%.
Answers
Answer:
24% i think i hope it the right answer
Step-by-step explanation:
how many null hypotheses are associated with a two-way anova?
Answers
There are actually three null hypotheses associated with a two-way ANOVA. These null hypotheses are related to the main effects of each of the two factors, as well as the interaction effect between the two factors. Each of these null hypotheses must be tested separately in order to fully understand the results of the ANOVA.
In a two-way ANOVA, there are three null hypotheses associated with the analysis. These hypotheses are used to examine the effects of two independent factors on a dependent variable. The three null hypotheses are as follows: 1. The first null hypothesis (H01) states that there is no significant effect of the first independent factor on the dependent variable, meaning that all the levels of the first factor have the same population mean. 2. The second null hypothesis (H02) states that there is no significant effect of the second independent factor on the dependent variable, meaning that all the levels of the second factor have the same population mean. 3. The third null hypothesis (H03) states that there is no interaction effect between the two independent factors on the dependent variable, meaning that the combined effect of the two factors is not significantly different from the sum of their individual effects.
To know more about null hypotheses visit :-
https://brainly.com/question/31898256
#SPJ11
2.5.1 Characterization Theorem
If S is a subset of R that contains at least two points and has the property
(1)
if x, y ES and
then S is an interval.
Proof. There are four cases to consider: (i) S is bounded, (ii) S is bounded above but not below, (iii) S is bounded below but not above, and (iv) S is neither bounded above nor below.
Case (i): Let a = inf S and b = sup S. Then SC[a, b] and we will show that (a, b)C S.
If a < z
Now if a S and b S, then S =[a, b]. (Why?) If a S and b S, then S=(a, b). The other possibilities lead to either S = (a, b) or S = [a, b).
Case (ii): Let b = sup S. Then SC (-[infinity]o, b] and we will show that (-oo, b)C S. For, if z
Cases (iii) and (iv) are left as exercises.
Answers
Cases (iii) and (iv) are left as exercises, meaning the proof for those cases is not provided in the given information. To fully establish the Characterization Theorem, the proof for these remaining cases needs to be completed.
Theorem 2.5.1 (Characterization Theorem):
If S is a subset of R that contains at least two points and has the property that if x, y ES and x < y, then (x, y)C S, then S is an interval.Proof.
There are four cases to consider:
(i) S is bounded,
(ii) S is bounded above but not below,
(iii) S is bounded below but not above, and
(iv) S is neither bounded above nor below.
Case (i): Let a = inf S and b = sup S.
Then SC[a, b] and we will show that (a, b)C S. If a < z < b, then there exist x, y
ES such that x < z < y. Since x < y and S has property (1), we have (x, y)C S.
Since zEP(x, y), it follows that zES.
Thus (a, b)C S.
Now if a S and b S, then S =[a, b].
If a S and b S, then S=(a, b).
The other possibilities lead to either S = (a, b) or S = [a, b].
Case (ii): Let b = sup S.
Then SC (-[infinity]o, b] and we will show that (-oo, b)C S. For, if z < b, then there exists y
ES such that z < y < b.
Since b is the least upper bound of S and yES, it follows that y 6S. But then (z, y)C (-oo, b) and (z, y)C S.
Thus (-oo, b)C S. Now if S contains its smallest element a, then S = [a, b]. Otherwise, S=(a, b).
Cases (iii) and (iv) are left as exercises.
For more questions on Characterization Theorem:
https://brainly.com/question/32506550
#SPJ8
Someone broke into my house and didn't steal anything, does this mean even robbers think i'm poor.
Answers
Answer:
Not really,maybe he just went in to find something,just that he didn't that's why maybe he didn't steal anything
Step-by-step explanation:
Answer:
Not necessarily. The robbers might've seen something or someone in your house and ran. They also could've heard something and thought you were home. So, if a robber breaks into your house but runs almost immediately you migt want to get your house checked out. Or, the robbers did think you were poor. Sorry.
Step-by-step explanation: