Estimate the amount of the tip by rounding the bill to the nearest 10 dollars before calculating
15% tip on a bill of $483.82
the amount of the tip is approximately $_.

Answer:

A is the best shows your answer

Answer:

B

Step-by-step explanation:

C and D are > and ≥ -18

A shows x < -18, which isn't what the question asks for

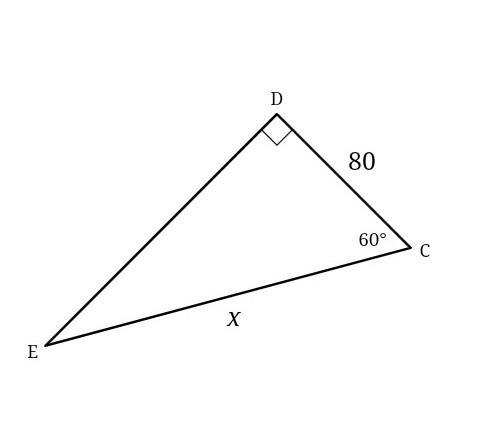
Answer:

Step-by-step explanation:

last one since if you plug in zero for the x in the denominator you get 0 and if you have 0 in the denominator it's always undefined

Answer:

58 boxes.

Step-by-step explanation:

First, we divide 462 by 8.

462 ÷ 8 = 57.75

Because you cannot have 0.75 of a box, you must have another box.

57 + 1 = 58.

The answer is 58 boxes.

Hope this helps!

Btw, could I get Brainliest? Thanks!

Answer:

2/4

Step-by-step explanation:

by

A power series solution z(x) of differential equation z" + z' - H3(z) = 0 exists, which is regular at x = 0. The Method of Frobenius is a powerful tool for solving differential equations, particularly when they have a regular singular point.

It involves assuming a power series solution and then solving for the coefficients of the series by matching the powers of x.In mathematics, a differential equation is a mathematical equation that involves functions and their derivatives.

It is a fundamental concept that is widely used in physics, engineering, and economics, among other fields. In particular, differential equations are used to model dynamic phenomena such as population growth, chemical reactions, and electrical circuits. The method of Frobenius is a powerful tool for solving differential equations of the form y'' + p(x)y' + q(x)y = 0.

It involves assuming a power series solution of the form y(x) = ∑ a_n x^n and then substituting this series into the differential equation. The coefficients of the series are then determined by solving a recursion relation. The method of Frobenius is particularly useful when the ordinary differential equation has a regular singular point.

A point x = x0 is a regular singular point if the coefficient functions p(x) and q(x) are analytic at x0. The method of Frobenius is then used to find a power series solution that is regular at x = x0. To apply the method of Frobenius to a differential equation, we assume that the solution can be written as a power series in x, and then substitute this series into the differential equation.

We then solve for the coefficients of the series by matching the powers of x on both sides of the equation. The method of Frobenius is often used in conjunction with other methods, such as the method of variation of parameters, to solve more complicated differential equations. The differential equation is given by z" + z' - H3(z) = 0, where u is a non-zero real number.

Using the method of Frobenius to find the power series expansion of a solution that is regular about x = 0;

let z = ∑ a_n x^(n+r),

z' = ∑ (n+r)a_n x^(n+r-1), and

z" = ∑ (n+r)(n+r-1)a_n x^(n+r-2).

Substituting the expressions for z, z', and z" into the differential equation, we get:

∑ (n+r)(n+r-1)a_n x^(n+r-2) + ∑ (n+r)a_n x^(n+r-1) - H3(∑ a_n x^(n+r)) = 0

We can re-index the series to begin at n = 0 to obtain:

∑ (n+r)(n+r-1)a_n x^(n+r-2) + ∑ (n+r)a_n x^(n+r-1) - H3(∑ a_n x^(n+r)) = 0

Starting with the first term of the second series, we have:

∑ (n+r)a_n x^(n+r-1) = ∑ (n+r)a_(n-1) x^(n+r-1) + ra_0 x^(r-1)

Using this formula to substitute for the second series in the equation above gives:

∑ (n+r)(n+r-1)a_n x^(n+r-2) + ∑ (n+r)a_(n-1) x^(n+r-1) + ra_0 x^(r-1) - H3(∑ a_n x^(n+r)) = 0

Multiplying out the last term on the left-hand side of the equation above gives:

∑ (n+r)(n+r-1)a_n x^(n+r-2) + ∑ (n+r)a_(n-1) x^(n+r-1) + ra_0 x^(r-1) - H3(a_0 x^r + a_1 x^(r+1) + a_2 x^(r+2) + ...) = 0

H3(a_0 x^r + a_1 x^(r+1) + a_2 x^(r+2) + ...) can be simplified by replacing each power of x in the series with (n+r) a_n x^(n+r-2).

Doing so gives:

H3(a_0 x^r + a_1 x^(r+1) + a_2 x^(r+2) + ...)

= H3 ∑ a_n (n+r) x^(n+r-2)

Combining like terms gives us the following:

∑ (n+r)(n+r-1)a_n x^(n+r-2) + ∑ [(n+r)a_(n-1) - H3a_n(n+r)] x^(n+r-1) + ra_0 x^(r-1) - H3a_0 x^r - H3a_1 x^(r+1) - H3a_2 x^(r+2) - ... = 0

Since the first term of the left-hand side is n=0, we can start the sum with n=0. Thus, the above equation becomes:  

a_1 [(r+1)u - H3] x^r + ∑ [(n+r)(n+r-1) + (n+r)(r+1)u - H3(n+r)] a_n x^(n+r) = 0

Dividing through by x^r gives:

a_1 [(r+1)u - H3] + ∑ [(n+r)(n+r-1) + (n+r)(r+1)u - H3(n+r)] a_n x^n = 0

We can now see that a_1 is free, while a_n can be solved recursively from a_(n+1). If we let α = (r+1)u - H3, then we can solve for a_1 as follows:

a_1 = α / (r+1)u

From the recursive relation above, we have:

a_(n+1) = [(H3 - (n+r)(n+r-1) - (n+r)(r+1)u) / (n+r+1)(n+2r+2)] a_n

To summarize, the power series expansion of the solution z(x) is: z(x) = ∑ a_n x^(n+r), where the coefficients a_n are given by:

a_0 is arbitrary,a_1 = α / (r+1)u, and a_(n+1)

= [(H3 - (n+r)(n+r-1) - (n+r)(r+1)u) / (n+r+1)(n+2r+2)] a_n.

We have therefore proved that a power series solution z(x) of the differential equation z" + z' - H3(z) = 0 exists, which is regular at x = 0. Hence proved.

Therefore, the method of Frobenius is a powerful tool for solving differential equations, particularly when they have a regular singular point. It involves assuming a power series solution and then solving for the coefficients of the series by matching the powers of x.

To know more about the method of Frobenius, visit :

brainly.com/question/31236446

#SPJ11

Answer:

$151,547

Step-by-step explanation:

Just got it right on a quiz.

This problem can be solved with integration. The first step is to integrate f '(t) dt. We use the integration formula for this purpose.The function f(t) has been found using the differential equation f'(t) = sec(t)(sec(t) tan(t))

f '(t) = sec(t)(sec(t) tan(t))

Integral calculus is used to find f(t) since it deals with derivatives.

Let's solve it.

f '(t) = sec(t)(sec(t) tan(t)) f(t) = ∫f '(t) dt

Using the integration formula,

f(t) = ∫ sec^2(t)dt = tan(t) + C [where C is the constant of integration]

f(t) = tan(t) + C

Now we have f(4) = -7. To find the value of C, we'll use

f(4) = -7=tan(4) + C7 = 1.1578 + C C = -7 - 1.1578 = -8.1578

Thus, the function

f(t) = tan(t) - 8.1578.

Therefore,The function f(t) has been found using the differential equation f'(t) = sec(t)(sec(t) tan(t))

In conclusion,f '(t) = sec(t)(sec(t) tan(t)) has been solved using integration. The value of the constant of integration, C, was found using the value of f(4) = -7. The function f(t) = tan(t) - 8.1578 is the solution to the differential equation.

To know more about differential equation visit:

brainly.com/question/32538700

#SPJ11

The most likely to generalize to it's population of interest is a stratified random sample of 120

a stratified random sample 120

Stratified random sampling is a method of sampling that involves the division of a population into smaller subgroups known as strata. In stratified random sampling, or stratification, the strata are formed based on members’ shared attributes or characteristics, such as income or educational attainment. Stratified random sampling has numerous applications and benefits, such as studying population demographics and life expectancy.

To learn more about stratified random sampling:

https://brainly.com/question/20692763

#SPJ4

113.09724, is the diameter of craig's balloon.

What is volume ?

The area or capacity of a cone is determined by its volume.

A cone's circular base tapers from a flat base to a point known as the apex or vertex in three dimensions.

A cone is made up of a collection of line segments, half-lines, or lines that connect the apex—the common point—to each point on the base, which is in a plane without the apex.

A cone can be thought of as a collection of irregularly shaped circular disks placed on top of one another with the ratio of their radii remaining constant.

A three-dimensional shape's volume is determined by how much space it takes up.

According to our question-

V = 4/3 * * r3 is the formula for a sphere's volume.

Your balloon's diameter is 6,

hence its radius is 3.

V = 4/3 * 3.14159 * 33 = 113.09724

Hence, 113.09724, is the diameter of craig's balloon.

Learn more about volume of cone click here:

brainly.com/question/1082469

#SPJ1

Negative 4 , negative 6 , negative 8 , negative 10.

An integer is a whole number that can be either positive, negative, or zero. It is not a fraction, decimal, or a percentage. Integers are the basic building blocks of mathematics and are used to represent whole numbers in equations. They are also used in computer programming languages to represent whole numbers.

negative 4 , negative 3 , negative 2 , negative 1,

−4, −5, −6, −7

negative 4 , negative 5 , negative 6 , negative 7,

−4, −2, 0, 2

negative 4 , negative 2 , 0, 2,

−4, −6, −8, −10

negative 4 , negative 6 , negative 8 , negative 10.
To know more about integer click-
https://brainly.com/question/929808
#SPJ1

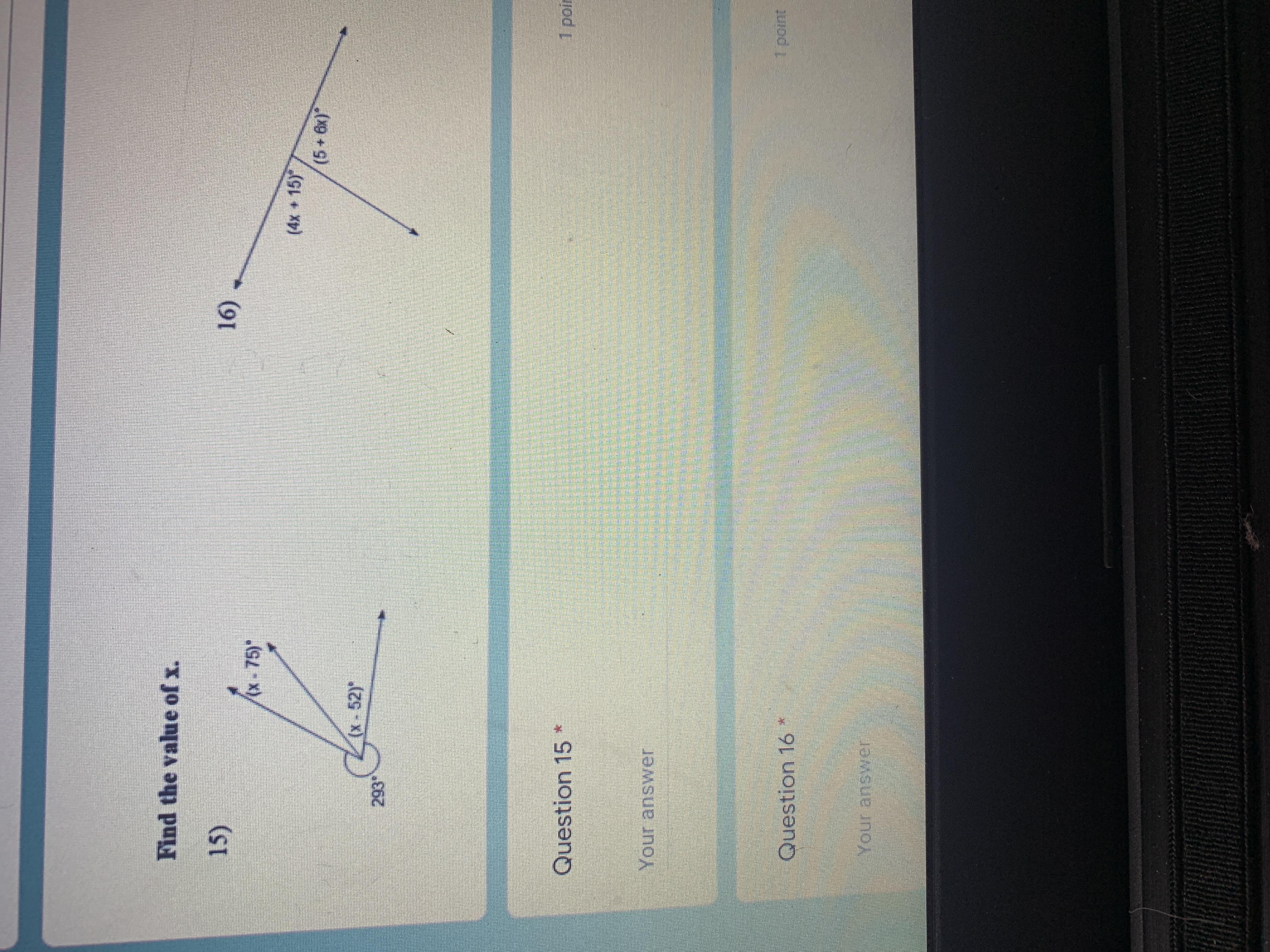
Answer:

Step-by-step explanation:

take 60 degree as reference angle

using cos rule

cos 60=adjacent/hypotenuse

1/2=80/x

x=80*2

x=160

Given :

\(\: {\qquad \sf \dfrac{4}{6} x + \dfrac{10}{4} = - \dfrac{6}{8}x - 10 }\)

⠀

To Find :

⠀

Solution :

\( {\qquad \sf \dashrightarrow \: \dfrac{4}{6} x + \dfrac{10}{4} = - \dfrac{6}{8}x - 10 }\)

⠀

Subtracting \( \sf \: \dfrac{10}{4} \) from both sides :

\( {\qquad \sf \dashrightarrow \: \dfrac{4}{6} x \: \: \cancel{+ \dfrac{10}{4}} \: \: \cancel{- \dfrac{10}{4}} = - \dfrac{6}{8}x - 10 - \dfrac{10}{4} }\)

⠀

Adding \( \sf \dfrac{6}{8} x\) to both sides :

\({\qquad \sf \dashrightarrow \: \dfrac{4}{6} x + \dfrac{6}{8}x = \cancel{- \dfrac{6}{8}x } \: \: \cancel {+ \: \dfrac{6}{8}x} - 10 - \dfrac{10}{4} }\)

\({\qquad \sf \dashrightarrow \dfrac{4}{6} x + \dfrac{6}{8}x = - 10 - \dfrac{10}{4}}\)

⠀

Adding the like terms :

\({\qquad \sf \dashrightarrow \dfrac{32x + 36x}{24} = \dfrac{ - 40 - 10}{4} }\)

\({\qquad \sf \dashrightarrow \dfrac{68x}{24} = \dfrac{ - 50}{4} }\)

\({\qquad \sf \dashrightarrow \dfrac{34x}{12} = \dfrac{ - 25}{2} }\)

⠀

By doing cross multiplication we get :

\({\qquad \sf \dashrightarrow {68x} = - 300 }\)

\({\qquad \sf \dashrightarrow {x} = \dfrac{ - 300}{68} }\)

\({\qquad \bf \dashrightarrow {x} = \dfrac{ - 75}{17} }\)

Answer:

16/3 = 5.333333333

Step-by-step explanation:

-8 x -2/3

Express -8(-2/3) as a single fraction

-8(-2)/3

Multiply −8 and −2 to get 16.

16/3 = 5.333333333

The equation is given, N(a) = 2.925 sin ( 3.65 ) + 12.18, which models the number of hours of daylight in New York City d days after March 21, 2010.

To solve the equation 11.5 = 2.925 sin (27 d) + 12.18 over the interval [0°, 720°), we need to isolate the sine function on one side of the equation.

Subtracting 12.18 from both sides, we get:
-0.68 = 2.925 sin (27 d)
Dividing both sides by 2.925, we get:
sin (27 d) = -0.2333
To find d, we need to use the inverse sine function (\(sin^{-1}\)) on both sides:
27 d = \(sin^{-1}\) (-0.2333)
Using a calculator, we find that \(sin^{-1}\) (-0.2333) = -13.5° or -0.235 radians (rounded to three decimal places).
Dividing both sides by 27, we get:
d = -0.0087 radians / 27
d = -0.00032 radians (rounded to five decimal places)
To make sense of this answer in the context of the problem, we need to convert radians to days.
One complete cycle of the sine function occurs over 360 degrees or 2π radians. Therefore, over the interval [0°, 720°), there are two complete cycles or 4π radians.
To find the number of days, we can set up a proportion:
4π radians = 365 days - 80 days (March 21 to June 9)
Solving for one radian, we get:
1 radian = (365 - 80) days / 4π
1 radian ≈ 71.3 days
Substituting this value, we get:
d = -0.00032 radians x 71.3 days/radian
d ≈ -0.023 days

Learn more about inverse sine function here:

https://brainly.com/question/28468393

#SPJ11

Answer: Five and a quarter

Step-by-step explanation:

Answer:

\(7h - 5(3h - 8) - 28 = 100 \\ 7h - 15h + 40 - 28 = 100 \\ 7h - 15h + 12 = 100 \\ - 8h + 12 = 100 \\ - 8h = 100 - 12 \\ - 8h = 88 \\ \frac{ - 8h}{ - 8} = \frac{88}{ - 8} \\ h = - 11\)

Step-by-step explanation:

100% = $6400

1% = 100%/100 = 6400/100 = $64

how many % are $448 of $6400 ?

we find out by calculating how often the 1% amount fits into the $448

448 / 64 = 7

so, his rate of commission was 7%.

Names of various geometric figures :Point, Line ,Line segment ,Ray, Angle ,Triangle ,Quadrilateral, Pentagon ,Hexagon and Circle

However, you didn't provide specific terms to include in the answer.

Regardless, I'll provide you with a list of common geometric figures:
1. Point: A single location in space.
2. Line: A one-dimensional figure that extends infinitely in both directions.
3. Line segment: A portion of a line with two endpoints.
4. Ray: A portion of a line with one endpoint and extends infinitely in the other direction.
5. Angle: Formed by two rays that share a common endpoint
6. Triangle: A polygon with three sides and three angles.
7. Quadrilateral: A polygon with four sides and four angles.
8. Pentagon: A polygon with five sides and five angles.
9. Hexagon: A polygon with six sides and six angles.
10. Circle: A closed curve with all points equidistant from a fixed point called the center.

for such more questions on  geometric figures

https://brainly.com/question/28247851

#SPJ11

Answer:

Rate when price rises 20% = $36

Rate when price downs 20% = $24

Step-by-step explanation:

Given:

Current rate to mow = $30 per lawn

Find:

Rate when price rises 20%

Rate when price downs 20%

Computation:

Rate when price rises 20%

Rate when price rises 20% = Current rate to mow + 20%[Current rate to mow]

Rate when price rises 20% = 30 + 20%[30]

Rate when price rises 20% = 30 + 6

Rate when price rises 20% = $36

Rate when price downs 20% = Current rate to mow - 20%[Current rate to mow]

Rate when price downs 20% = 30 - 20%[30]

Rate when price downs 20% = 30 - 6

Rate when price downs 20% = $24

The four points with y-coordinates half their x-coordinates are (0,0), (2,1), (4,2), and (6,3). These points do lie on a line, as they all satisfy the linear equation y = x/2.

To plot four points whose y-coordinates are half their x-coordinates, we can choose any four values of x and then compute the corresponding values of y using the equation y = x/2. For example

If x = 0, then y = 0/2 = 0, so the first point is (0,0).

If x = 2, then y = 2/2 = 1, so the second point is (2,1).

If x = 4, then y = 4/2 = 2, so the third point is (4,2).

If x = 6, then y = 6/2 = 3, so the fourth point is (6,3).

We can plot these points on a coordinate plane

As we can see from the plot, the four points do lie on a straight line. This is because the equation y = x/2 is the equation of a linear function with slope 1/2 and y-intercept 0. Therefore, any two points on this line will have a constant slope between them, and thus the four points will be collinear.

Learn more about coordinates plane here

brainly.com/question/24134413

#SPJ4

Answer: 15) 97

16) 16

17) 24

Step-by-step explanation:

15) (x-75) + (x-52)+ 293=360

x - 75 + x - 52 + 293 = 360

2x - 127 + 293 = 360

2x + 166 = 360

        2x  = 194           [Subtract 166 from both side]

          x  = 97             [Divide by 2 from both side]

16) (4x+15)+(5+6x)=180         The angle of a straight line is 180.

4x + 15 + 5 + 6x = 180

10x + 20 = 180

        10x = 160            [Subtract 20 from both side]

            x = 16               [Divide by 10 from both side]

17) (x+17)+(2x+1)= 90               These two angle combined equal to 90.

x + 17 + 2x + 1 = 90

3x + 18 = 90          

3x = 72                         [Subtract 18 from both side]

x = 24                           [Divide by 3 from both side]

The model that is most likely rule out on the basis of this simulation is 40%

Probability is the function that measures the chances that an outcome of a random event will be as expected. In this way you can measure how likely it is that an event will happen.

First set of trials:  ththththht ( where T = Tails ; H = Heads)

Number of heads = 5

Number of outcomes = 10

Second set of trials: ttthtthtth

Number of heads = 3

Number of outcomes = 10

Total number of heads = 5 + 3 = 8

Total number of outcomes = 10 + 10 = 20

Probably of heads = 8/20 * 100%

Probably of heads = 0.4*100%

Probably of heads = 40%

Learn more about probability at: brainly.com/question/251701

#SPJ4

Answer:

f[g(1)]=6.

Explanation:

Given f(n) and g(n) defined below:

First, we evaluate g(1):

Therefore:

Therefore, f[g(1)]=6.

Answer:

yea

Step-by-step explanation:

Answer:

The answer is 0.00024.

Step-by-step explanation:

Answer: -5/4

Step-by-step explanation:

A slope is also known as the gradient of a line. The slope of the given equation is -5/4.

A slope also known as the gradient of a line is a number that helps to know both the direction and the steepness of the line.

slope = (y₂-y₁)/(x₂-x₁)

The given line passes through two points (0,2) and (-4,7), therefore, the slope of the given line can be written as,

Slope, m = (7 - 2)/(-4 - 0) = 5/-4

Hence, the slope of the given equation is -5/4.

Learn more about Slope of Line here:

https://brainly.com/question/14511992

#SPJ2