explain to someone how you know that if the results of a hypothesis test are significant at the 5% level, you don’t know if the results are significant at the 1% level.
Answers
Significance at a 5% level means the obtained p-value is less than 0.05, but it doesn't indicate significance at a 1% level since the latter requires even stronger evidence to reject the null hypothesis.
When we conduct a hypothesis test, we set a significance level, typically denoted as alpha, which represents the threshold for determining the level of evidence required to reject the null hypothesis. The most commonly used significance levels are 5% (0.05) and 1% (0.01).
If the results of a hypothesis test are found to be significant at the 5% level, it means that the obtained p-value (probability value) is less than 0.05. In other words, the observed data is considered statistically significant at a 5% level of significance, indicating that the evidence against the null hypothesis is strong enough to reject it.
However, it is important to note that a result being significant at the 5% level does not necessarily imply that it will be significant at the 1% level. A 1% level of significance requires even stronger evidence to reject the null hypothesis. Therefore, if the p-value obtained in the test is greater than 0.01, we cannot conclude statistical significance at the 1% level, even if it is significant at the 5% level.
In summary, the choice of significance level determines the threshold for accepting or rejecting the null hypothesis. If a result is significant at a lower significance level (e.g., 1%), it automatically implies significance at higher significance levels (e.g., 5%). However, a result being significant at a higher significance level does not guarantee significance at a lower level, as the stricter criteria for rejection are not met.
Learn more about hypothesis here:
https://brainly.com/question/32969759
#SPJ11
Related Questions
Factor By Grouping.
54 − 63 + 24 − 28
Step By Step Explanation Please
Answers
Answer:
-13
Step-by-step explanation:
Calculate the sum positive numbers
54-63+24-28
= 78-63-28
Calculate the sum of the negative numbers
78(-63-28)
= 78-91
=-13
what is value of the "2" in 32,405
Answers
Answer:
please mark me brainliest
Step-by-step explanation:
thousandth
The place Value of 2 is Thousand (1000)
Hope it helped youcan you guys help me please as much as you can ^^

Answers
Answer:
Step-by-step explanation:
m<1 = 50
m<2 = 22
m<3 = 108
m<4 = 50
m<5 = 65
m<6 = 50
m<7 = 43
m<8 = 65
m<9 = 75
m<10 = 18
m<11 = 25
m<12 = 40
m<13 = 115
m<14 = 65
m15 = 115
t a certain high school, for seniors, the odds in favor of planning to attend college are 3.57 to 1. Of juniors at the same high school, 0.75 proportion plan to attend college. Round your final answer to each part to three decimal places, but do not round during intermediate steps. (a) For seniors, the proportion who plan to attend college is (b) For juniors, the odds in favor of planning to attend college are to 1.
Answers
The odds in favor of juniors planning to attend college are 3 to 1.
(a) For seniors, to find the proportion who plan to attend college, we can use the odds given:
Odds = (Number planning to attend college) : (Number not planning to attend college)
3.57 : 1
To convert odds to proportion, we can use the formula:
Proportion = (Number planning to attend college) / (Total number of seniors)
We know that the total number of seniors is the sum of those planning and not planning to attend college:
Total number of seniors = 3.57 + 1 = 4.57
Now, we can calculate the proportion:
Proportion (seniors) = 3.57 / 4.57 = 0.781
Rounding to three decimal places, the proportion of seniors planning to attend college is 0.781.
(b) For juniors, we are given the proportion who plan to attend college, which is 0.75. To find the odds in favor, we can use the formula:
Odds = (Number planning to attend college) : (Number not planning to attend college)
Since the proportion of juniors planning to attend college is 0.75, this means that 75% plan to attend and 25% do not. To express this as odds, we can set the number planning to attend college as 75 and the number not planning to attend as 25:
Odds (juniors) = 75 : 25
Now, we can simplify the ratio:
Odds (juniors) = 3 : 1
So, the odds in favor of juniors planning to attend college are 3 to 1.
visit here to learn more about Proportion:
brainly.com/question/24232216
#SPJ11
Which choice is equivalent to 6(y-3)+2y-2
A. 8y-20
B. 4y-20
C. 8y-5
D. 8y-16
Answers
Answer: its 8y-20
You need to rmove the parenthesis and combine like terms
use the app m a t h w a y ! yw have a good day
Sanjay sold 8kg of sugar at Rs 28 per kg and earned a profit of Rs 40 What was the cost price per kg
Answers
Answer:
23
Step-by-step explanation:
8 kg * 28 per kg = Rs. 224
Profit = Rs. 40
CP = SP - Profit
224 - 40
184
184 / 8
23
What is the SI Unit of measurement of Angle?
A. Degree
B. Radian
C. Steradian
D. Minutes
Answers
Answer:
B. Radian
Step-by-step explanation:
I remember learning this in math class. Radian is SI Unit of measurement of Angle.
Find a vector parallel to the line of intersection of the planes given by the equations 2x - 3y + 5z = 2 and 4x + y - 3z = 7
Answers
The vector <-32, 44, 22> is parallel to the line of intersection of the two planes given by the equations 2x - 3y + 5z = 2 and 4x + y - 3z = 7.
To find a vector parallel to the line of intersection of the planes given by the equations 2x - 3y + 5z = 2 and 4x + y - 3z = 7, we first need to find the direction vector of the line of intersection.
We can find the direction vector by taking the cross product of the normal vectors of the two planes. The normal vector of the plane 2x - 3y + 5z = 2 is <2, -3, 5>, and the normal vector of the plane 4x + y - 3z = 7 is <4, 1, -3>. Taking the cross product of these two vectors, we get:
<2, -3, 5> × <4, 1, -3> = <-16, 22, 11>
This vector <-16, 22, 11> is the direction vector of the line of intersection of the two planes.
To find a vector parallel to this line, we can simply multiply the direction vector by a scalar. For example, we can choose a scalar of 2 to get:
2<-16, 22, 11> = <-32, 44, 22>
Therefore, the vector <-32, 44, 22> is parallel to the line of intersection of the two planes given by the equations 2x - 3y + 5z = 2 and 4x + y - 3z = 7.
Learn more about line of intersection here
https://brainly.com/question/31743634
#SPJ11
Complete the square
x^2 - 2x - 14 = 0
Answers
To complete the square for the equation x^2 - 2x - 14 = 0, follow these steps:
1. Move the constant term to the right side of the equation: x^2 - 2x = 14
2. Take half of the coefficient of x, square it, and add it to both sides of the equation: x^2 - 2x + 1 = 15
3. Factor the left side of the equation as a perfect square: (x - 1)^2 = 15
4. Take the square root of both sides of the equation, remembering to include both the positive and negative square roots: x - 1 = ±√15
5. Add 1 to both sides of the equation to isolate x: x = 1 ± √15
Therefore, the solutions to the equation x^2 - 2x - 14 = 0 are x = 1 + √15 and x = 1 - √15.
One week, seventy-two percent of the animals that cam to a veterinary hospital were dogs. If there were 230 animals total, how many were dogs
Answers
Answer:
165.6
Step-by-step explanation:
165.6 is 72% of 230
Which of the following intervals corresponds to the smallest area under a Normal curve?
a) Q1 to Q3
b) μ to μ + 3σ
c) Q1 to μ + 2σ
d) μ - σ to Q3
Answers
The area under a Normal curve depends on the interval being considered and the parameters of the Normal distribution, such as its mean and standard deviation.
To determine which of the given intervals corresponds to the smallest area under a Normal curve, we need to consider the properties of the Normal distribution. The Normal distribution is a symmetric bell-shaped curve that is completely determined by its mean and standard deviation. The mean, denoted by µ, is the center of the curve, while the standard deviation, denoted by σ, determines the spread of the curve.
Option b) µ to µ + 3σ corresponds to the interval that covers almost all the area under a Normal curve, as about 99.7% of the area lies within three standard deviations of the mean. Therefore, this option cannot correspond to the smallest area under a Normal curve.
Option a) Q1 to Q3 and option d) µ - σ to Q3 both cover more area than option c) Q1 to µ + 2σ. The interval Q1 to Q3 covers the entire middle 50% of the distribution, while the interval µ - σ to Q3 covers at least 50% of the distribution, as almost all the area lies within three standard deviations of the mean. Therefore, option c) Q1 to µ + 2σ corresponds to the smallest area under a Normal curve.
In summary, the interval corresponding to the smallest area under a Normal curve is option c) Q1 to µ + 2σ.
Learn more about Normal distribution here
https://brainly.com/question/4079902
#SPJ11
write an equation of a polynomial with x intercepts of 0, 10, -15 and passes through the point (2, -136)
Answers
Answer:
f(x) = 0.5x^3 + 2.5x^2 - 75x
Step-by-step explanation:
To write the equation of a polynomial with given x-intercepts and passing through a point, we can use the factored form of the polynomial:
f(x) = a(x - r1)(x - r2)(x - r3) ...
where r1, r2, r3, ... are the x-intercepts, and a is a constant that scales the polynomial vertically. Since the x-intercepts are 0, 10, and -15, we can write:
f(x) = a(x - 0)(x - 10)(x + 15)
Expanding this expression gives:
f(x) = a(x^3 + 5x^2 - 150x)
To find the value of a, we can use the fact that the polynomial passes through the point (2, -136):
-136 = a(2^3 + 5(2^2) - 150(2))
Simplifying this equation gives:
-136 = -272a
Dividing both sides by -880 gives:
a = 0.5
Therefore, the equation of the polynomial is:
f(x) = 0.5x^3 + 2.5x^2 - 75x
find the z value for 0.99 if e O¨zlem likes jogging 3 days of a week. She prefers to jog 3 miles. For her 95 times, the mean wasx¼ 24 minutes and the standard deviation was S¼2.30 minutes. Let μ be the mean jogging time for the entire distribution of O¨zlem’s 3 miles running times over the past several years. How can we find a 0.99 confidence interval for μ?.
likes jogging 3 days of a week. She prefers to jog 3 miles. For her 95 times, the mean wasx¼ 24 minutes and the standard deviation was S¼2.30 minutes. Let μ be the mean jogging time for the entire distribution of O¨zlem’s 3 miles running times over the past several years. How can we find a 0.99 confidence interval for μ
a) What is the table value of Z for 0.99? (Z0.99)? (b) What can we use for σ ? (sample size is large) (c) What is the value of? Zcσffiffin p (d) Determine the confidence interval level for μ.
Answers
a. The table value of z 0.99 is given as 2.58.
b. we use σ = 2.30 minutes.
c. The value of Z is given as 0.609.
d. The confidence interval is (23.391, 24.609) minutes.
How to solve for the z critical valuea) To find the z-score for a 0.99 confidence interval, we need to find the z-score that leaves 0.5% (since it's two-tailed, we split the 1% or 0.01 of the data that's not within the confidence interval into two) in each tail. The z-score for 0.995 (0.5% in the upper tail) is approximately 2.58 in standard normal distribution tables. So, Z_0.99 is 2.58.
b) Therefore, we use σ = 2.30 minutes.
c) The standard error of the mean (SE) is given by σ/√n, where n is the sample size.
Here, σ = 2.30 minutes and n = 95.
Therefore, SE = σ/√n
= 2.30/√95
= 0.236 minutes.
Multiply this by the z-score to find Z * σ/√n.
Therefore, Z * σ/√n = 2.58 * 0.236 ≈ 0.609.
d) The 0.99 confidence interval for μ
Here, x is the sample mean which is 24 minutes.
So the confidence interval is approximately
= (24 - 0.609, 24 + 0.609)
= (23.391, 24.609) minutes.
This is the range of values we are 99% confident that the true population mean (μ) falls in.
Read more on Z critical here:https://brainly.com/question/14040224
#SPJ4
_____ lateral faces of a rectangular pyramid are congruent.
Adjacent
Opposite
All of the
Answers
Answer:
Opposite
------------------------------------
Select the statement that best describes SST. Question 3 options: SST measures the variability of the actual data. SST measures the variability between the data and the best guess at a linear model of the data. A large SST guarantees that the independent and dependent variables are related. A low SST minimizes the error between the data's actual y values and the model's y values.
Answers
SST measures the variability of the actual data.
SST, or the Total Sum of Squares, is a statistical measure that quantifies the total variability observed in the data. It represents the total variation of the dependent variable (y) without considering any specific model or independent variables.
SST measures the dispersion or spread of the actual data points around their mean. It provides an overall assessment of the total variability present in the data set, regardless of any relationships or models. By calculating the sum of the squared differences between each data point and the mean of the data, SST captures the total variation or deviation from the mean value.
The other options presented do not accurately describe SST. While SST is related to the variability in the data, it does not measure the variability between the data and a linear model (that would be measured by SSE, or Sum of Squares Error). SST also does not guarantee the presence of a relationship between independent and dependent variables, nor does it aim to minimize the error between actual y values and model y values.
In summary, SST represents the total variation in the data and is a fundamental measure in statistical analysis. It provides insights into the overall spread or dispersion of the observed data points, regardless of any specific models or relationships.
Learn more about Actual data.
brainly.com/question/31430138
#SPJ11
A relation contains the points (1, 2), (2, -1), (3, 0), (4, 1), and (5, -1). Which statement accurately describes this relation?
Answers
Answer:
J The relation represents y as a function of x, because each value of x is associated with a single value of y.
Step-by-step explanation:
I'm sure of this
Answer:
H
Step-by-step explanation:
i think so i’m not one hundred percent sure though ! Tell me if i’m wrong
The perimeter of the triangle below is 97 cm.
What is the length of EF?
A. 18 cm
B. 23 cm
C. 30 cm
D. 32 cm
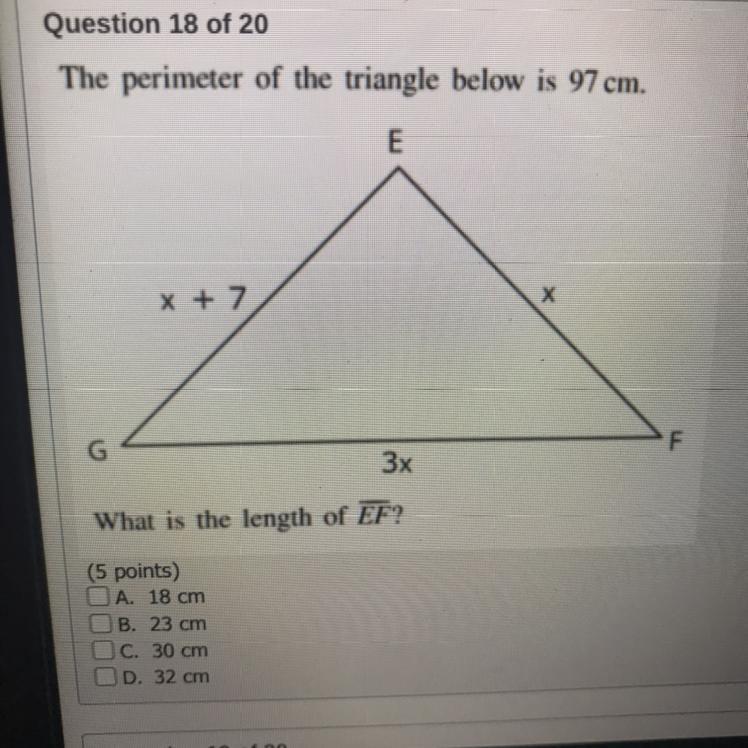
Answers
Answer:
The length of EF = x = 18 cm
Option A is correct.
Step-by-step explanation:
Ware given perimeter of triangle = 97 cm
We need to find length of EF = x = ?
The length of EG = x+7
The length of EF = x
The length of GF = 3x
The formula used is: \(Periemter \ of \ triangle= Sum \ of \ all \ sides \ of \ triangle\)
Putting values and finding x i.e length of EF
\(Periemter \ of \ triangle= Sum \ of \ all \ sides \ of \ triangle\\97=x+7+x+3x\\97-7=5x\\5x=90\\x=\frac{90}{5}\\x=18 \ cm\)
So, value of x=18 cm
The length of EF = x = 18 cm
Option A is correct.
How much money will there be in an account at the end of 9 years if $18000 is deposited at 7% interest compounded semi-annually? (Assume no withdrawals are made.)
Answers
There will be $33434.8 in the account after 9 years
How much money will there be in an accountFrom the question, we have the following parameters that can be used in our computation:
Principal, P = 18000
Time = 9 years
Rate = 7%
Number of times = 2
The formula for calculating the amount in an account is
A = P * (1 + r/2)^(2t)
So, the amount in the account after 9 years will be:
A = $18000 * (1 + 0.07/2)^(2 * 9)
Evaluate
A = $33434.8
Hence, after 9 years there will be $33434.8 in the account.
Read more about compound interest at
https://brainly.com/question/28020457
#SPJ1
Let F™= (5z +5x4) i¯+ (3y + 6z + 6 sin(y4)) j¯+ (5x + 6y + 3e²¹) k." (a) Find curl F curl F™= (b) What does your answer to part (a) tell you about JcF. dr where Cl is the circle (x-20)² + (-35)² = 1| in the xy-plane, oriented clockwise? JcF. dr = (c) If Cl is any closed curve, what can you say about ScF. dr? ScF. dr = (d) Now let Cl be the half circle (x-20)² + (y - 35)² = 1| in the xy-plane with y > 35, traversed from (21, 35) to (19, 35). Find F. dr by using your result from (c) and considering Cl plus the line segment connecting the endpoints of Cl. JcF. dr =
Answers
Given vector function is
F = (5z +5x4) i¯+ (3y + 6z + 6 sin(y4)) j¯+ (5x + 6y + 3e²¹) k
(a) Curl of F is given by
The curl of F is curl
F = \((6cos(y^4))i + 5j + 4xi - (6cos(y^4))i - 6k\)
= 4xi - 6k
(b) The answer to part (a) tells that the J.C. of F is zero over any loop in \(R^3\).
(c) If C1 is any closed curve in\(R^3\), then ∫C1 F. dr = 0.
(d) Given Cl is the half-circle
\((x - 20)^2 + (y - 35)^2\) = 1, y > 35.
It is traversed from (21, 35) to (19, 35).
To find the line integral of F over Cl, we use Green's theorem.
We know that,
∫C1 F. dr = ∫∫S (curl F) . dS
Where S is the region enclosed by C1 in the xy-plane.
C1 is made up of a half-circle with a line segment joining its endpoints.
We can take two different loops S1 and S2 as shown below:
Here, S1 and S2 are two loops whose boundaries are C1.
We need to find the line integral of F over C1 by using Green's theorem.
From Green's theorem, we have,
∫C1 F. dr = ∫∫S1 (curl F) . dS - ∫∫S2 (curl F) . dS
Now, we need to find the surface integral of (curl F) over the two surfaces S1 and S2.
We can take S1 to be the region enclosed by the half-circle and the x-axis.
Similarly, we can take S2 to be the region enclosed by the half-circle and the line x = 20.
We know that the normal to S1 is -k and the normal to S2 is k.
Thus,∫∫S1 (curl F) .
dS = ∫∫S1 -6k . dS
= -6∫∫S1 dS
= -6(π/2)
= -3π
Similarly,∫∫S2 (curl F) . dS = 3π
Thus,
∫C1 F. dr = ∫∫S1 (curl F) . dS - ∫∫S2 (curl F) . dS
= -3π - 3π
= -6π
Therefore, J.C. of F over the half-circle is -6π.
To know more about half-circle visit:
https://brainly.com/question/30312024?
#SPJ11
round the numbers to estimate the quotient 29 1/5 divided by 4 6/7
Answers
Answer:
The anwser is 6.01176470588
What would u say if ur math teacher asks u this?!

Answers
Answer:
undecided
Step-by-step explanation:
Solve the equation.
7h-5(3h-8)= -72
Answers
7h-15h+40=-72
40+72=15h-7h
112=8h
h=14
Given that BD is both the median and altitude of ABC, congruence postulate
SAS is used to prove that ABC is what type of triangle?

Answers
Answer:
isosceles
Step-by-step explanation:
An isosceles triangle is one with two equal-length sides. The correct option is D.
What is an isosceles triangle?An isosceles triangle is one with two equal-length sides. It is sometimes stated as having exactly two equal-length sides, and sometimes as having at least two equal-length sides, with the latter form containing the equilateral triangle as a particular case.
Any triangle, whose median is also the altitude of the triangle is an isosceles triangle. Since it is given that BD is both the median and altitude of ΔABC. Therefore, the given ΔABC is an isosceles triangle.
Learn more about Isosceles Triangle:
https://brainly.com/question/2456591
#SPJ5
The measure of the missing angle is

Answers
Answer:
43
Step-by-step explanation:
92 + 45+43=180
HOPE THIS HELPS
Answer:
It looks like forty-five degrees, maybe a little lower
Step-by-step explanation:
that's my estimate without a protractor.
Anita paid a total of $57.50 for a blazer. The price of the blazer was $52.85. What was the sales tax rate?
Answers
Answer:
8.79 % tax rate
Step-by-step explanation:
total paid = tax + price
57.50 = tax +52.85
tax = 4.65
tax rate =( tax ÷ price before the tax) × 100%
= (4.65÷ 52.85) × 100%
= 8.79%
Answer:8.08%
Write the expression in standard form a+bi: (8-i)/(2+i)
Answers
Answer:
The expression (8-i)/(2+i) in standard form is, 3 - 2i
Step-by-step explanation:
The expression is,
(8-i)/(2+i)
writing in standard form,
\((8-i)/(2+i)\\\)
Multiplying and dividing by 2+i,
\(((8-i)/(2+i))(2-i)/(2-i)\\(8-i)(2-i)/((2+i)(2-i))\\(16-8i-2i-1)/(4-2i+2i+1)\\(15-10i)/5\\5(3-2i)/5\\=3-2i\)
Hence we get, in standard form, 3 - 2i
The expression (8-i)/(2+i) in standard form a+bi is (15 - 10i) / (3 + 4i).
To write the expression (8-i)/(2+i) in standard form a+bi, we need to eliminate the imaginary denominator. We can do this by multiplying the numerator and denominator by the conjugate of the denominator.
The conjugate of 2+i is 2-i. So, we multiply the numerator and denominator by 2-i:
(8-i)/(2+i) * (2-i)/(2-i)
Using the distributive property, we can expand the numerator and denominator:
(8(2) + 8(-i) - i(2) - i(-i)) / (2(2) + 2(i) + i(2) + i(i))
Simplifying further:
(16 - 8i - 2i + i^2) / (4 + 2i + 2i + i^2)
Since i^2 is equal to -1, we can substitute -1 for i^2:
(16 - 8i - 2i + (-1)) / (4 + 2i + 2i + (-1))
Combining like terms:
(15 - 10i) / (3 + 4i)
Therefore, the expression (8-i)/(2+i) in standard form a+bi is (15 - 10i) / (3 + 4i).
Learn more:About complex numbers here:
https://brainly.com/question/20566728
#SPJ11
Alicia has £100 in a savings account. Each year, the amount of money in her account increases by 20%. How much money will be in the account after 4 years?
Answers
Answer:£207.36
Step-by-step explanation:
Pls help and show workings
It due in a hour

Answers
Answer:
13
Step-by-step explanation:
i answered this for someone else a little bit ago and i got a thanks on it and i chose that answer because 13 is already on the triangle and n is too small to match up with the 13cm
solve the equation for x and enter your answer below. 7= x - (-12)
Answers
Answer:
-5 =x
Step-by-step explanation:
7= x - (-12)
Subtracting a negative is like adding
7 = x+12
Subtract 12 from each side
7-12 = x+12-12
-5 =x
Answer:
-5
Step-by-step explanation:
add 7 and -12
you will get "-5"
so then you do "-5- (-12)"
PS!! The "-5" is what your x equals!
so after you add those you should get "7"
This is probably the easiest way to do it especially when you get older
What is the area of a triangle whose vertices are D(1, 1), E(3, -1), and F(4, 4)?
Enter your answer in the box.
Answers
Answer:
6
Step-by-step explanation:
Trust