Factor the expression using the GCF 10w + 50z
Answers
Answer:
The GCF is 10
Step-by-step explanation:
What is the smallest number that can be multiplied to get 10 and 50?
10 = 2^1 × 5^1
Factors 1, 2, 5, 10
50 = 21 × 52
Factors 1, 2, 5, 10, 25
GCF = 10
Related Questions
A 40 gram sample of a substance that’s used for drug research has a k-value of 0.1472.
Find the substance’s half-life, in days. Round your answer to the nearest tenth.
Answers
A 40 gram sample of a substance that’s used for drug research has a k-value of 0.1472. The substance's half-life, in days, is approximately 4.7 days.
The half-life of a substance is the time it takes for half of the substance to decay or undergo a transformation. The half-life can be determined using the formula:
t = (0.693 / k)
where t is the half-life and k is the decay constant.
In this case, we are given that the sample has a k-value of 0.1472. We can use this value to calculate the half-life.
t = (0.693 / 0.1472) ≈ 4.7 days
Therefore, the substance's half-life, rounded to the nearest tenth, is approximately 4.7 days.
For more such questions on k-value, click on:
https://brainly.com/question/1978047
#SPJ8
used to measure the center of a set of values. good for summarizing values that are generally pretty similar to each other.
Answers
Mean is used to measure the center of a set of values. It is good for summarizing values which are generally pretty similar to each other.
What is mean and its function?Mean is more usually referred to as the average. It is calculated by adding up all of the values and dividing by the total number of values. It is a good way for summarizing the center of values which are commonly very similar to each other.
The mean is the most often used measure of central tendency since it uses all values in the data set to give us an average. For data from skewed distributions, the median is better than the mean because it is not influenced by large values.
Learn more about mean at: https://brainly.com/question/30090607
#SPJ4
Although part of your question is missing, you might be referring to this full question: _________ is used to measure the center of a set of values. It is good for summarizing values that are generally pretty similar to each other.
prove l’hˆopital’s rule: if f(z) and g(z) are analytic at z0 and f(z0) = g(z0) = 0, but g 0 (z0) 6= 0, then limz→z0 f(z) g(z) = f 0 (z0) g 0(z0)
Answers
The f(z)/(z - z0) is analytic at z0 and its limit is f’ 0 (z0). This completes the proof of l'Hôpital's rule
To prove l'Hôpital's rule, we can use the Cauchy integral formula. Let D be a small disk centered at z0 and with radius r. Then we have:
f(z) = (1/2πi) ∫γ f(ζ)/(ζ - z) dζ,
where γ is the boundary of D oriented counterclockwise. Similarly, we have:
g(z) = (1/2πi) ∫γ g(ζ)/(ζ - z) dζ.
Since f(z0) = g(z0) = 0 and g' 0 (z0) ≠ 0, we can expand g(z) as:
g(z) = g’ 0 (z0) (z - z0) + O((z - z0)²).
Then, for z in D, we have:
f(z) g(z) = f(z) [g’ 0 (z0) (z - z0) + O((z - z0)²)]
= g’ 0 (z0) [f(z)/(z - z0)] (z - z0) + O((z - z0)³).
Note that the O((z - z0)²) and O((z - z0)³) terms are bounded by Cr² and Cr³, respectively, where C is a constant depending on f and g but independent of r. Using the Cauchy integral formula again, we have:
f(z)/(z - z0) = (1/2πi) ∫γ f(ζ)/(ζ - z) dζ
= (1/2πi) ∫γ [f(ζ) - f(z0)]/(ζ - z0) dζ.
Since f(z0) = 0, the integrand is bounded by M/r for some constant M depending on f but independent of r. Therefore, we have:
|f(z)/(z - z0)| ≤ M/r
for all z in D except z0. Thus, the term (z - z0) cancels out in the limit as z approaches z0, and we get:
limz→z0 f(z) g(z) = limz→z0 g’ 0 (z0) [f(z)/(z - z0)] (z - z0)
= g’ 0 (z0) f’ 0 (z0),
where we used the fact that f(z)/(z - z0) is analytic at z0 and its limit is f’ 0 (z0). This completes the proof of l'Hôpital's rule.
Learn more about Analytic
brainly.com/question/30279876
#SPJ11
Is Rainbow Six Siege Good
Answers
Answer:
yes beacuse he have nice grapics and u can play with your friends.
Step-by-step explanation:
Answer: Yes it is very good i recommend getting it, but it takes a ton of time to get use to it.
Step-by-step explanation:
17. What is 18,000,000,000,000 written in scientific notation?
A
1.8 x 10-13
В.
1.8 x 10"
C.
18 x 10-12
D.
18 x 1012

Answers
Greetings! I hope this helps!
Answer:
D: 18 x 10^12
Explanation:
Scientific notation is basically simplifying a huge number. So you have 18 and 12 0's. So its 18 x 10^12 (to the twelfth power)
Find the value of x in the diagram.
Pls help

Answers
Answer:
72
Step-by-step explanation:
Answer:
72 degrees
Step-by-step explanation:
x = 360 - (108 + 121 + 59)
x = 360 - (108 + 180)
x = 360 - 288
x = 72 degrees
Hope that helps!
CAYB is a quadrilateral
CA= 3a
CB= 6b
BY= 5a-b
X is the point on AB such that AX:XB= 1:2
Prove that CX = 2/5 CY

Answers
Answer:
see explanation
Step-by-step explanation:
CY = CB + BY
= 6b + 5a - b
= 5a + 5b
---------------------
CX = CA + AX
= CA + \(\frac{1}{3}\) AB , find AB
AB = AC + CB
= - 3a + 6b
= 6b - 3a
Thus
CX = CA + \(\frac{1}{3}\) AB
= 3a + \(\frac{1}{3}\)(6b - 3a)
= 3a + 2b - a
= 2a + 2b
---------------------
and
\(\frac{2}{5}\) CY
= \(\frac{2}{5}\) (5a + 5b)
= 2a + 2b = CX
Hence CX = \(\frac{2}{5}\) CY ⇒ Proven
What is the circumference of a circle that has a diameter of 9cm?
Answers
Answer:
28.27
Step-by-step explanation:
C=2piR
c=(2)(3.1415926535)(4.5)
= approximately 28.27
28.27....................k?
1 What is the domain of the following function?
A -4
B 4≤x≤1.5
C -5
D -5≤y≤6

Answers
The domain of the function is -4 ≤ x ≤ 1.5. The correct answer is option B.
What is Domain ?
A domain is the possible independent variable value of a function. In a two dimensional graph, the independent variable is x - axis.
From the given graph, tracing the line of the equation to the x - axis, the independent variable value span from x = -4 to x = 1.5.
So, we can say that the domain of the function is -4 ≤ x ≤ 1.5
Therefore, the correct answer is option B.
Learn more about Domain here: https://brainly.com/question/2264373
#SPJ1
please help im stuck on this

Answers
Is the answer :)
centers of triangles circumcenter and incenter worksheet
Answers
The circumcenter can be present at where the intersection of angle bisectors is present and whereas incenter is present at the intersection of perpendicular bisectors of a line.
What is triangle ?
Triangle can be defined in which it consists of three sides , three angles and the sum of three angles is always 180 degrees.
They bisected of the angles and observed that the perspective bisectors crossed. They drew the 0.33 bisector and surprised to discover that it too went thru the same factor. They should have notion this became just a coincidence. but after they drew any triangle they located that the attitude bisectors continually intersect at a unmarried point! This ought to be the 'center' of the triangle. Or so they notion.
After some experimenting they observed different unexpected things. for instance the altitudes of a triangle additionally pass via a unmarried point (the orthocenter). but no longer the identical factor as earlier than. another middle! Then they discovered that the medians skip via but any other single factor. not like, say a circle, the triangle manifestly has more than one 'middle'.
The points wherein these various lines go are referred to as the triangle's points of concurrency.
Therefore, The circumcenter can be present at where the intersection of angle bisectors is present and whereas incenter is present at the intersection of perpendicular bisectors of a line.
To learn more about Triangle from given link.
https://brainly.com/question/2773823
#SPJ1
Hello please answer this it is due at 11:59 and im panicking please. Thank you so much

Answers
Answer:
that an isosceles triangle with equal indicated sides implies that the remaining angle is also x..(angles opp to equal sides are equal)so basically we have two x's in that triangle along with that 41.now x+x+41=180 (Sum of interior angles of a triangle)2x=180-41 hence x=69.5°if you are dividing 1.7 by 8.5 how many places to the right will you need to move the decimal point in the divisor and dividend
Answers
Answer:
To divide 1.7 by 8.5, you will need to move the decimal point one place to the right in the divisor and the dividend. This would result in 17 and 85 as the new divisor and dividend respectively, and the division would be performed as 17/85.
Four-inch pieces are repeatedly cut from a 48-inch string. The length of the string after x cuts is given by y=48 - 4x.
Find and interpret the x and y intercepts. State the meaning of each in the contest of the situation
Answers
The x-intercept is 12 and represents the number of pieces and the y-intercept is 48 and represents the initial length.
What is a linear function?A straight line on the coordinate plane is represented by a linear function.
In another word, a linear function is a function that varies linearly with respect to the changing variable.
As per the given function,
y = 48 - 4x
At x-intercept, y = 0
48 - 4x = 0
x = 12
Since x is the number of cuts so it represents that we can cut 12 pieces.
At y-intercept , x = 0
y = 48
Since 48 is the initial length so it represents the initial length.
Hence "The beginning length is represented by the y-intercept, which is 48, and the number of pieces is represented by the x-intercept, which is 12".
For more about the linear function,
brainly.com/question/21107621
#SPJ1
Which equations are true equations?
Select all correct answers.
62−22=4+7⋅22
54 ÷ 6 + 3² = 4 + 4²
8042=10−22−1
19−2⋅5=9⋅73−9
Answers
We want to see which ones of the given equations are true equations. Here we will see that the only true equation is the second one:
54 ÷ 6 + 3² = 4 + 4²
We define a true equation as an equation where the thing at the left is equal to the thing on the right, so we need to check that for all the given equations.
1) 62 − 22 = 4 + 7⋅22
We just solve each side, we will get:
40 = 158
This is not a true equation.
2) 54 ÷ 6 + 3² = 4 + 4²
9 + 9 = 4 + 16
18 = 18
This is a true equation.
3) 8042 = 10 − 22 − 1
Clearly, this is not a true equation.
4) 19 − 2⋅5 = 9⋅73 −9
19 - 10 = 657 - 9
9 = 648
This is not a true equation.
Then the only true equation is the second one:
54 ÷ 6 + 3² = 4 + 4²
If you want to learn more, you can read:
https://brainly.com/question/21834784
You are 5 1/3 feet tall. you must be at least 5 1/2- feet tall to ride a roller coaster. write and solve an equation to represent how much taller you must be to ride the roller coaster
Answers
The equation h>= 11/2 feet represents the required height of an individual to ride the roller coaster.
Your height = 5 1/3 feet tall
Required height in feet to ride a roller coaster = at least 5 1/2 feet
When the numerator exceeds or is equal to the denominator, the fraction is said to be improper. 5/2 and 8/5, for instance, are improper fractions.
Let h represent the height
h>= 5 1/2
Converting into an improper fraction
h>= 11/2 feet
Your height in improper fraction = 16/3 feet
Comparing the required height and your height we find that
Required height>Your height
Learn more about fractions:
https://brainly.com/question/10354322
#SPJ1
Brainliest!!!!! Please Help
Can these curves be the graphs of functions? (Hint: use the vertical line test.)


Answers
I WILL GIVE BRAINILY (20 PTS)
There are 15 questions, and John got an 84% on the quiz, how many questions did John get right and how many wrong?
Answers
Answer:
John got 13 questions right and 2 questions wrong.
Step-by-step explanation:
15 questions right equals 100%.
100 {divided by} 15 = % for each question right
Each question is worth (100 diveded by 15) 6.7%.
84% {diveded by} 6.7% = 12.5
100% - 84% = 16%
16% {divided by} 6.7% = 2.38
Because 12.5 has a higher dicimle value than 2.38 and when the amount he got right is added to the amount he got wrong it needs to equal 15, 12.5 becomes 13 and 2.38 becomes 2.
Answer:
\(\frac{n}{15} =\frac{84}{100}\)
\(n = \frac{21}{25}*5\)
\(n = \frac{21*15}{25}\)
\(n = \frac{315}{25}\)
\(n = \frac{63}{5} or 12.6\)
a researcher wants to know which exercise program: 1) a fast walking program, or 2) a running program is most effective in reducing the risk of a myocardial infarction. the researcher anticipates that the target heart rate for the program is an important additional variable that needs to be considered. the researcher will recruit 100 volunteers from a local exercise facility in a large retirement community. subjects must be between 70 to 80 years old, willing to follow the assigned program three days a week for up to ten years, and with no serious heart disease or other problems that would limit participation in the exercise programs. subjects will be randomly assigned to one of four groups: 1) fast walking for 30 minutes at a pace and at an incline adequate to keep the heart rate in the range of 55-65% of the age-adjusted maximum heart rate, 2) fast walking for 30 minutes at a pace and at an incline adequate to keep the heart rate in the range of 70-80% of the age-adjusted maximum heart rate, 3) running for 30 minutes at a pace and at an incline adequate to keep the heart rate in the range of 55-65% of the age-adjusted maximum heart rate, 4) running for 30 minutes at a pace and at an incline adequate to keep the heart rate in the range of 70-80% of the age-adjusted maximum heart rate. subjects will be followed for 10 years and the number of mis will be compared among the four groups. in the walking and running study related to heart rate, which is the dependent variable?
Answers
The dependent variable is:
(4) running for 30 minutes at a pace and at an incline adequate to keep the heart rate in the range of 70-80% of the age-adjusted maximum heart rate.
Both exercise program and percentage of the age-adjusted maximum heart rate are Dependent Variable.
Dependent variables are studied under the assumption or claim that they depend on the values of other variables according to some law or rule (for example, by a mathematical function). In turn, the independent variables were not considered dependent on any other variable in the context of the associated experience.
In this sense, some common independent variables are time, space, density, mass, fluid velocity, and past values of some observations of interest (e.g., population size) to predict future values (dependent variable).
An example of a dependent variable is depressive symptoms, which depends on the independent variable (type of treatment). In an experiment, a researcher investigates the effect that changing an independent variable might have on a dependent variable.
Learn more about Dependent Variable:
https://brainly.com/question/29430246
#SPJ4
What is the slope-intercept equation for the linear function represented by the
table?

Answers
Answer: y= 3/2x - 6
Step-by-step explanation:
The equation is y=mx + b
The y-intercept is when x = 0, so on the table y-intercept = -6
The slope is rise/run, we see that y increase by three and x increase by 2, so the slope is 3/2
to get the slope of any straight line, we simply need two points off of it, let's use those ones in the picture below.
\((\stackrel{x_1}{2}~,~\stackrel{y_1}{-3})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{3}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{3}-\stackrel{y1}{(-3)}}}{\underset{run} {\underset{x_2}{6}-\underset{x_1}{2}}} \implies \cfrac{3 +3}{4} \implies \cfrac{ 6 }{ 4 } \implies {\Large \begin{array}{llll} \cfrac{3 }{ 2 } \end{array}}\)
now, the y-intercept occurs when x = 0, recheck the picture below.

use analytic methods to find (a) the local ex- trema, (b) the intervals on which the function is increasing, and (c) the intervals on which the function is decreasing
Answers
Use analytic methods,
(a) The local extrema,
1) If f'(x) > 0 for all x on (a , c) and f'(x)<0 for all x on (c , b), then f(c) is a local maximum value.
2) If f'(x) < 0 for all x on (a , c) and f'(x)>0 for all x on (c , b), then f(c) is a local maximum value.
(b) The intervals on which the function is increasing
Write properties of function :
Increasing interval : ( - ∞ , 0 )
(c) The intervals on which the function is decreasing
Write properties of function :
Decreasing interval : ( 0 , ∞ )
Given that,
Use analytic methods (a) the local extrema, (b) the intervals on which the function is increasing, and (c) the intervals, then the function is,
A function's growing (or decreasing) periods match the periods when its derivative is positive (or negative). As a result, we can easily determine the intervals where a function increases or decreases by taking its derivative and analyzing it to determine if it is positive or negative.
(a) How do we find the local extrema?Let f be continuous on an open interval (a , b) that contains a critical x-value.
1) If f'(x) > 0 for all x on (a , c) and f'(x)<0 for all x on (c , b), then f(c) is a local maximum value.
2) If f'(x) < 0 for all x on (a , c) and f'(x)>0 for all x on (c , b), then f(c) is a local maximum value.
(b) The intervals on which the function is increasing
Write properties of function :
Increasing interval : ( - ∞ , 0 )
(c) The intervals on which the function is decreasing
Write properties of function :
Decreasing interval : ( 0 , ∞ )
Therefore,
Use analytic methods,
(a) The local extrema,
1) If f'(x) > 0 for all x on (a , c) and f'(x)<0 for all x on (c , b), then f(c) is a local maximum value.
2) If f'(x) < 0 for all x on (a , c) and f'(x)>0 for all x on (c , b), then f(c) is a local maximum value.
(b) The intervals on which the function is increasing
Write properties of function :
Increasing interval : ( - ∞ , 0 )
(c) The intervals on which the function is decreasing
Write properties of function :
Decreasing interval : ( 0 , ∞ )
To learn more about Analytic methods visit :
brainly.com/question/19463434
#SPJ4
Determine the slope (8grade

Answers
Answer: 1/2
Step-by-step explanation: I believe the answer is 1/2 because for (2,-6) and (4,-7) the rise over run is 1/2. I don't know though
A cork has a mass of 3.00 grams and a volume of 16.0 cm3. Calculate the density.
Answers
Answer:
0.1875
Step-by-step explanation:
5
Match each expression with its quotient.
a. 5.2 10
b. 520 - 10²
c. 52 - 10³
d. 5,200 10¹
0.052
0.52
5.2
52
520
5,200
Answers
The appropriate matching of the expression will be:
5.2 × 10 = 52
5.2 × 10² = 520
5.2 × 10³ = 5200
5.2 × 10^-1 = 0.52
How to illustrate the information?It should be noted that the information illustrated is simply about the power on the numbers. This was illustrated on the information.
In this case, it should be noted that the thing to f is to multiply the numbers or count the number of zeros and illustrate on the numbers.
Therefore, the appropriate matching of the expression will be:
5.2 × 10 = 52
5.2 × 10² = 520
5.2 × 10³ = 5200
5.2 × 10^-¹ = 0.52
Learn more about expressions on:
brainly.com/question/25968875
#SPJ1
The number of moose in Alaska at the start of year n is Pn
The number of moose in Alaska at the start of the following year is given by
Pn+1 = 1.04(Pn - G) where G is a constant
At the beginning of 2015, there were 200 000 moose in Alaska.
At the beginning of 2016, there were 200 720 moose in Alaska.
Work out how many moose there were in Alaska at the beginning of 2017
Answers
Population having expression Pn+1 = 1.04(Pn - G), there were approximately 220,863 moose in Alaska at the beginning of 2017.
What exactly are expressions?
In mathematics, an expression is a combination of numbers, variables, and operators that represents a mathematical quantity or relationship. Expressions can be composed of numbers, variables, and operators such as addition, subtraction, multiplication, division, and exponentiation.
Now,
We are given that:
At the beginning of 2015 (n = 0), P0 = 200,000
At the beginning of 2016 (n = 1), P1 = 200,720
The formula for calculating the number of moose at the start of the following year is Pn+1 = 1.04(Pn - G), where G is a constant.
To find the value of P2 (the number of moose at the beginning of 2017), we can use the formula with n = 1:
P2 = 1.04(P1 - G)
We need to find the value of G. We can use the information given to us at the beginning of 2015 and 2016 to form two equations:
P1 = 1.04(P0 - G)
P2 = 1.04(P1 - G)
We can use substitution to solve for G. Rearranging the first equation, we get:
P0 - G = (P1/1.04)
G = P0 - (P1/1.04)
Substituting this expression for G into the second equation, we get:
P2 = 1.04(P1 - (P0 - (P1/1.04)))
Simplifying and solving for P2, we get:
P2 = 220,863 (rounded to the nearest whole number)
Therefore,
there were approximately 220,863 moose in Alaska at the beginning of 2017.
To know more about expressions visit the link
brainly.com/question/13947055
#SPJ1
The serving size of a nutrition label is 3/4 of a cup. How much servings are in an 12 cup box?
Answers
Answer:
16 servings
Step-by-step explanation:
Divide 12 by 3/4
12/1 ÷ 3/4 = 12/1 x 4/3
12/1 x 4/3 = 48/3
Ans 16
Quadrilateral WXYZ has the coordinates W(b, b), X(4b, b), Y(3b, 0), and Z(0, 0).
What is the length of side W X
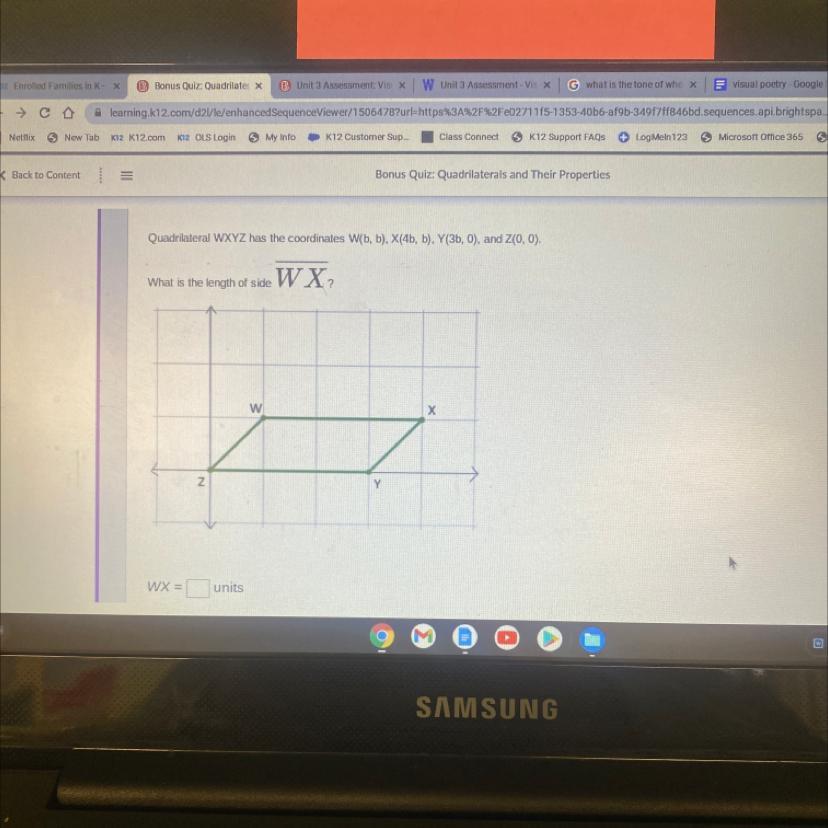
Answers
The length of side WX in Quadrilateral WXYZ is 3b units.
Coordinate planeThe distance between two points A(x₁, y₁) and B(x₂, y₂) on the coordinate plane is given by:
\(AB=\sqrt{(y_2-y_1)^2+(x_2-x_1)^2} \)
Given the coordinates W(b, b), X(4b, b), Y(3b, 0), and Z(0, 0). The length of WX is:
\(WX=\sqrt{(b-b)^2+(4b-b)^2}=3b \)
The length of side WX in Quadrilateral WXYZ is 3b units.
Find out more on coordinate plane at: https://brainly.com/question/26100648
A wireless company offers two cell phone plans. For the month of September Plan A charges $35 plus $0.25 per minute for calls. Plan B charges $20 plus $0.50 per minute for calls. For what number of minutes do both plans cost the same amount?
i really need help
Answers
Answer:
3.75 minutes
Step-by-step explanation:
Set up an equation where x is the number of minutes:
0.25x + 35 = 0.5x + 20
Solve for x:
0.25x + 35 = 0.5x + 20
35 = 0.25x + 20
15 = 0.25x
3.75 = x
So, both plans will cost the same with 3.75 minutes
Use cofunctions of complementary angles to complete the relationship. cos (pi/3)=sin() Find the lengths of the missing sides if side a is opposite angle A, side b cos(B) = 4/5, a = 50
Answers
The relationship between cosine and sine of complementary angles allows us to complete the given equation. Using the cofunction identity, we know that the cosine of an angle is equal to the sine of its complementary angle.
If cos(pi/3) = sin(), we can determine the value of the complementary angle to pi/3 by finding the sine of that angle. To find the lengths of the missing sides in a right triangle, we can use the given information about the angle B and side a. Since cos(B) = 4/5, we know that the adjacent side (side b) is 4 units long and the hypotenuse is 5 units long. Using the Pythagorean theorem, we can find the length of the remaining side, which is the opposite side (side a). Given that a = 50, we can solve for the missing side length. In summary, using the cofunction identity, we can determine the value of the complementary angle to pi/3 by finding the sine of that angle. Additionally, using the given information about angle B and side a, we can find the missing side length by using the Pythagorean theorem.
Learn more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ11
a = 9 m, b = 4 m and c = 13 m for the triangle shown below.