find an expressing that is equivalent to
2 ( x - 3 ) ²
Answers
x(2x-12)+18
Related Questions
15 oranges weigh 3. 75 kilograms (kg). If each orange weighs approximately the same, approximately how much does each orange weigh?
Answers
4 kg
So approximately each orange weighs 4 kilograms.
the lengths of two sides of a rectangle are in the ratio $2:3.$ the area of the rectangle is $864.$ what is the perimeter of the rectangle?
Answers
The perimeter of the rectangle is 120.
Based on the problem, the lengths of two sides of a rectangle are in the ratio 2 : 3.
Let 2x be the length of the shorter side while the length of the longer side will be equal to 3x.
2 : 3 = 2x : 3x
If the area of the rectangle is 864, then
A = lw
A = 3x(2x)
864 = 6x²
Solve for the value of x.
864 = 6x²
x² = 144
x = 12
Hence, the length of the shorter side will be 24 while the length of the longer side is equal to 36.
Solve the perimeter of the rectangle.
P = 2l + 2w
P = 2(36) + 2(24)
P = 120
Therefore, the perimeter of the rectangle is equal to 120.
Learn more about perimeter here: https://brainly.com/question/19819849
#SPJ4
Solve the inequality. -11x+8x( greater then or equal to)13
Answers
Answer:
I think its answer is -3x > or equal to 13
Step-by-step explanation:
-11x+8x > or equal to 13
=-3x > or equal to 13
if a line has a y-axis intercept of b and a x-axis of a, express the slope of this line in terms of a and b
slope=
Answers
The slope of this line in terms of a and b is b/a
Express the slope of this line in terms of a and bfrom the question, we have the following parameters that can be used in our computation:
Intercepts = b and a
The slope of this line in terms of a and b is calculated as
Slope = y/x
Substitute the known values in the above equation, so, we have the following representation
Slope = b/a
HEnce, the slope is b/a
Read more about slope at
https://brainly.com/question/33472030
#SPJ1
describe the graph of the solution

Answers
First, we want to note two things:
We have a solid circle at -10, so -10 IS part of the solution.We have shading to the right of -10, meaning we also need to include numbers to the right of -10, or numbers greater than -10.
We can describe this with an inequality: x ≥ -10
Be sure you use ≥ and not >, since -10 is included.
We can describe this with interval notation: [ -10, infty )
Be sure you use [ and not ( on -10, since -10 is included.
You can also use set-builder notation: { x | x ≥ -10 }
Five employees are available to perform four jobs. The lime it takes each person to perform each job is given in Table 50. Determine the assignment of employees to jobs that minimizes the total time required to perform the four jobs.
TABLE 50
Person
Time (hours)
Job 1
Job 2
Job 3
Job 4
1
22
18
30
18
2
18
—
27
22
3
26
20
28
28
4
16
22
—
14
5
21
—
25
28
Answers
To determine the assignment of employees to jobs that minimizes the total time required to perform the four jobs, we need to consider the time taken by each person to complete each job. Using the given Table 50, we can analyze the data and identify the optimal assignment.
By examining Table 50, we can identify the minimum time taken by each person for each job. Starting with Job 1, we see that Person 4 takes the least time of 16 hours. Moving to Job 2, Person 2 takes the least time of 18 hours. For Job 3, Person 1 takes the least time of 25 hours. Lastly, for Job 4, Person 4 takes the least time of 14 hours.
Therefore, the optimal assignment would be:
- Person 4 for Job 1 (16 hours)
- Person 2 for Job 2 (18 hours)
- Person 1 for Job 3 (25 hours)
- Person 4 for Job 4 (14 hours)
This assignment ensures that the minimum total time is required to perform the four jobs, resulting in a total time of 16 + 18 + 25 + 14 = 73 hours.
To learn more about minimize total time click here: brainly.com/question/15071332
#SPJ11
2y+3/3y-8=3/2
find the value of y
Answers
Answer:
y=6
Step-by-step explanation:
Multiply both sides by 3y-8.
2y+3=9y/2-12
Add 12 to both sides.
2y+15=9y/2
Multiply both sides by 2.
Subtract both sides by 4y.
30=5y
Divide both sides by 5.
Therefore, y=6.
Answer:
2y+3/3y-8=3/2
multiply through by 3
3(2y+3-8)= (3/2)*3
6y-5= 9/2
6y =9/2+5
6y=19/2
y= 19*6/2
y= 57
1060 divided by 48 as a mixed number
Answers
Answer:
When you divide 1060 by 48, your answer will be 22.08333... ( decimal) but when rounded, it will either be 22, 22.1, or 22.08 (just for rounding, you do not have to put this in.)
Hope this helped!
Step-by-step explanation:
Answer:
22 1/12
Step-by-step explanation:
48*22=1056
1060-1056=4
= 22 4/48
= 22 1/12
So the answer is 22 1/12,
Hope this helps!
3. Why do communities need healthy citizens?
Citizens who are healthy watch T.V. a lot and buy what they see in commercials.
O Citizens who are healthy contribute more to their communities.
Citizens who are healthy create more problems for their communities.
Citizens who are healthy move from place to place.
Answers
Answer:
B
Step-by-step explanation:
O Citizens who are healthy contribute more to their communities.
( I don't think this is math related).
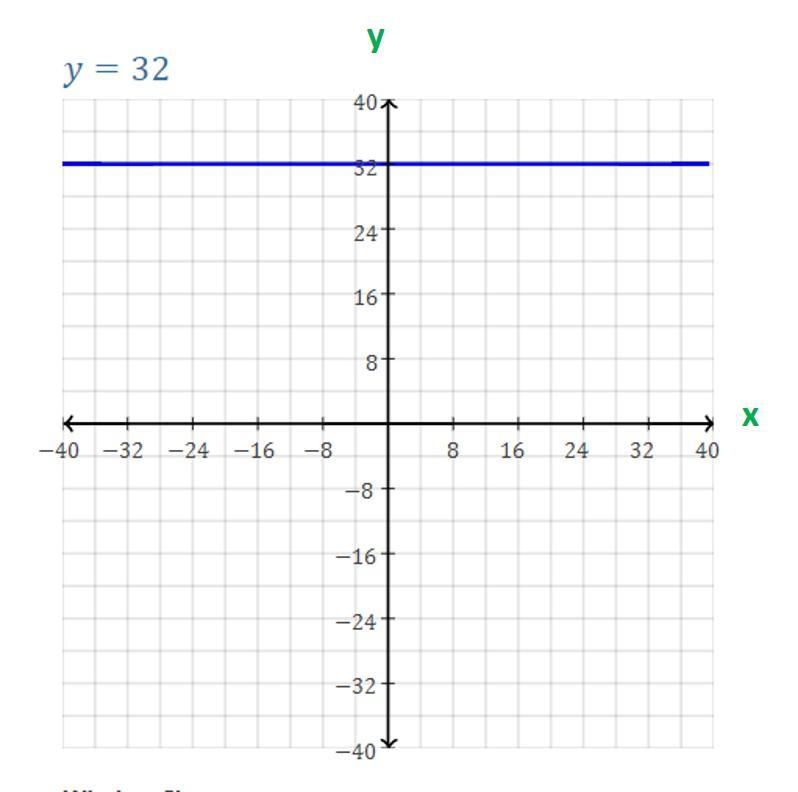
Graph the function f(x) = 32. Plot the key features including any x- and y-intercepts, any vertical, horizontal, or slant asymptotes, and any holes.
Answers
The graph of the function f(x) = 32 is attached accordingly.
How would you describe the above graph ?X - Intercept - There is no x-intercept since the function is a horizontal line.
Y -Interept - The y-intercept is (0, 32), since the line intersects the y-axis at y = 32.
Vertical Asymptotes - There are 0 vertical asymptotes, since t function is defined for all values of x.
Horizontal Asymptotes - There are 0 horizontal asymptotes, since the function is a horizontal line.
Slant Asymptotes - There are zeroslant asymptotes, since the function is a horizontal line.
Holes - There are zeroholes in the graph, since the function is a horizontal line with no breaks or discontinuities.
Learn more about graphs:
https://brainly.com/question/17267403
#SPJ1
Answer: see below
Step-by-step explanation:
got it right on quiz

Answer this easy geometry question

Answers
Answer:
1684.8 cubic units
Step-by-step explanation:
In oblique cylinder the height (altitude) is measured from the opposite base to the base of the cylinder, but it lies outside. We can find the height using Pythagoras theorem.
h + 7² = 13²
h²= 169 - 49
h² = 120
h = √120
h = 10.95 units
radius = r = 7 units
\(\boxed{\text{\bf Volume of oblique cylinder = $\bf\pi r^2h$} }\)
= 3.14 * 7 * 7 * 10.95
= 1684.8 cubic units
PLEASE HELP FAST) A ship travels 10 miles from Point A to Point B, makes a turn of 112, and
travels 16 miles to Point C. If the ship travels directly from Point C back to
Point A, how many miles will it travel on the last leg of the trip (from Point C
to Point A)? Round your answer to the nearest tenth of a mile.
O A. 19.2 miles
B. 23.4 miles
O C. 21.8 miles
D. 25.2 miles

Answers
Answer:
B
Step-by-step explanation:
maybe
If S={a,b,c} with P(a)=2P(b)=3P(c), find P(a). 9. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c) and P(d)=P(e)=P(f)=0.1, find P(a). 10. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c), P(d)=P(e)=P(f), and P(d)=2P(a), find P(a). 11. If E and F are two disjoint events in S with P(E)= 0.2 and P(F)=0.4, find P(E∪F),P(E
c
), and P(E∩F). 12. Why is it not possible for E and F to be two disjoint events in S with P(E)=0.5 and P(F)=0.7? 13. If E and F are two disjoint events in S with P(E)= 0.4 and P(F)=0.3, find P(E∪F),P(F
c
),P(E∩F), P((E∪F)
c
), and P((E∩F)
c
). 14. Why is it not possible for S={a,b,c} with P(a)= 0.3,P(b)=0.4, and P(c)=0.5 ?
Answers
Since the total probability of the sample space S must be equal to 1, it is not possible for three events with probabilities that add up to more than 1 to form the sample space.
9. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c) and P(d)=P(e)=P(f)=0.1, find P(a).
Since P(a), P(b), and P(c) are equal, we can let P(a) = P(b) = P(c) = x.
Then, we know that P(d) = P(e) = P(f) = 0.1.
The total probability of the sample space S is equal to 1. So, we can write the equation:
P(a) + P(b) + P(c) + P(d) + P(e) + P(f) = 1
Substituting the given values, we get:
3x + 0.1 + 0.1 + 0.1 = 1
3x + 0.3 = 1
3x = 1 - 0.3
3x = 0.7
Dividing both sides by 3, we find:
x = 0.7/3
So, P(a) = 0.233.
10. If S={a,b,c,d,e,f} with P(a)=P(b)=P(c), P(d)=P(e)=P(f), and P(d)=2P(a), find P(a).
Let P(a) = P(b) = P(c) = x. And let P(d) = P(e) = P(f) = y.
We also know that P(d) = 2P(a).
Using the equation for the total probability:
P(a) + P(b) + P(c) + P(d) + P(e) + P(f) = 1
We can substitute the given values:
3x + 3y = 1
We also know that P(d) = 2P(a):
y = 2x
Substituting this into the previous equation:
3x + 3(2x) = 1
3x + 6x = 1
9x = 1
Dividing both sides by 9, we find:
x = 1/9
So, P(a) = P(b) = P(c) = 1/9.
11. If E and F are two disjoint events in S with P(E)=0.2 and P(F)=0.4, find P(E∪F), P(Ec), and P(E∩F).
Since E and F are disjoint, their intersection, E∩F, is empty.
The probability of the union of two disjoint events is the sum of their individual probabilities:
P(E∪F) = P(E) + P(F) = 0.2 + 0.4 = 0.6
The complement of E, Ec, is the event that consists of all outcomes in S that are not in E.
The complement of an event has a probability equal to 1 minus the probability of the event:
P(Ec) = 1 - P(E) = 1 - 0.2 = 0.8
Since E and F are disjoint, their intersection, E∩F, is empty, so its probability is 0:
P(E∩F) = 0
12. It is not possible for E and F to be two disjoint events in S with P(E)=0.5 and P(F)=0.7 because the sum of their probabilities would exceed 1.
Since the total probability of the sample space S must be equal to 1, it is not possible for two events with probabilities that add up to more than 1 to be disjoint.
13. If E and F are two disjoint events in S with P(E)=0.4 and P(F)=0.3, find P(E∪F), P(Fc), P(E∩F), P((E∪F)c), and P((E∩F)c).
Since E and F are disjoint, their intersection, E∩F, is empty.
The probability of the union of two disjoint events is the sum of their individual probabilities:
P(E∪F) = P(E) + P(F) = 0.4 + 0.3 = 0.7
The complement of F, Fc, is the event that consists of all outcomes in S that are not in F.
The complement of an event has a probability equal to 1 minus the probability of the event:
P(Fc) = 1 - P(F)
= 1 - 0.3
= 0.7
Since E and F are disjoint, their intersection, E∩F, is empty, so its probability is 0:
P(E∩F) = 0
The complement of the union of two events, (E∪F)c, is the event that consists of all outcomes in S that are not in the union of E and F.
The complement of an event has a probability equal to 1 minus the probability of the event:
P((E∪F)c) = 1 - P(E∪F) = 1 - 0.7 = 0.3
The complement of the intersection of two events, (E∩F)c, is the event that consists of all outcomes in S that are not in the intersection of E and F.
The complement of an event has a probability equal to 1 minus the probability of the event:
P((E∩F)c) = 1 - P(E∩F) = 1 - 0 = 1
14. It is not possible for S={a,b,c} with P(a)=0.3, P(b)=0.4, and P(c)=0.5 because the sum of their probabilities exceeds 1.
Since the total probability of the sample space S must be equal to 1, it is not possible for three events with probabilities that add up to more than 1 to form the sample space.
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
Mindy and Troy combined ate 999 pieces of the wedding cake. Mindy ate 333 pieces of cake and Troy had \dfrac14 4 1 start fraction, 1, divided by, 4, end fraction of the total cake. Write an equation to determine how many pieces of cake (c)(c)left parenthesis, c, right parenthesis there were in total. Find the total number of pieces of cake. Pieces of cake
Answers
The total number of pieces of cake will be 2664
A linear equation is an algebraic equation with simply a constant and a first-order (linear) component of the form y=mx+b, where m is the slope and b is the y-intercept.
The above is sometimes referred to as a "linear equation with two variables," where y and x are the variables.
Ax+By=C is the typical form for linear equations in two variables.
2x+3y=5, for example, is a simple linear equation.
It is rather simple to get both intercepts when an equation is stated in this way (x and y).
Let c be the total number of pieces of cake.
We know that Mindy ate 333 pieces and Troy ate 1/4 of the total,
So, we can write it as:
333 + (1/4)c = 999
Expanding the second term:
333 + c/4 = 999
Solving for c:
c/4 + 333 = 999
Subtracting 333 from both sides:
c/4 = 666
Multiplying both sides by 4:
c = 2664
For more questions on Linear Equation
https://brainly.com/question/25858757
#SPJ4
find the sum by adding each term together. use the summation capabilities of a graphing utility to verify your result. 6 k
Answers
To find the sum of 6k by adding each term together, we can simply add 6k + 6k + 6k + 6k + 6k + 6k which gives us a total of 36k.
To verify this result using the summation capabilities of a graphing utility, we can use the sigma notation (Σ) to represent the sum. The sigma notation is defined as Σ6k where k starts at 1 and goes up to 6. This means we are adding 6k, six times.
To input this into a graphing utility, we can use the summation feature. For example, on a TI-84 calculator, we can press the "Math" button, select "1:sum(", and enter the expression "6k" followed by a comma and then the values of k that we want to sum from (1) and to (6). This gives us the result of 36k, which matches our previous calculation.
Learn more about graphing utility:
https://brainly.com/question/29260419
#SPJ11
Do I find the HCF for this or the LCM?? Please help quickly

Answers
Step-by-step explanation:
You are looking for the LCM of 15 and 42
PLEASE HELP!!
The diagram shows the cross-section ABCD of a sculpture in the shape of
a prism
with perpendicular height 9 cm.
AB = 14 cm, CD = 8cm, AD = 12cm and BC = 10cm
The height of the prism is also 9 cm.
What is the total surface area of the sculpture in cm2?
Type each step of your working on a separate line.

Answers
Answer:
99 (cm^2)
Step-by-step explanation:
Perpendicular to the AB segment at points D and C, the graph is divided into two triangles and a rectangle.
The area of the middle rectangle is equal to 8*9=72. The hypotenuse of the right triangle is 10cm, and one of the right sides is 9cm, so the other side is SQRT (10^2-9^2) = SQRT (19).
One side of the left triangle is 9cm long and the other side is 14-8-sqRT (19) = 6-sqRT (19) cm.
Then, add the area of the three parts.
72+9*sqrt(19)/2+9*(6-sqrt(19))/2=99 (cm^2)
The market for smart thermostats has grown increasingly competitive. Producers of smart thermostats all rely on the same technology and face the same costs. The cost function for a smart thermostat producer is given by the following function:
c(y)= 3
y 3
−10y 2
+200y, where
y
stands for the number of smart thermostats produced and sold in a month. 1st attempt O See Hint Suppose the market demand for smart thermostats in any month is given by
Q D
=275−p.
In the long-run equilibrium, we would expect to find firms in the industry
Answers
Based on the given cost function and demand function, we can find the long-run equilibrium by setting the marginal cost equal to the marginal revenue.
The marginal cost is given by the derivative of the cost function:
MC(y) = 9y^2 - 20y + 200
The marginal revenue can be found by taking the derivative of the demand function and solving for p:
QD = 275 - p
p = 275 - QD
MR = d(QD)/dy * dp/dy = -1
Setting MC = MR:
9y^2 - 20y + 200 = -1
Simplifying and solving for y:
9y^2 - 20y + 201 = 0
Using the quadratic formula: y = (20 ± sqrt(400 - 4*9*201)) / 18
Since the discriminant is negative, there are no real solutions for y. This means there is no long-run equilibrium for this market.
In practical terms, this suggests that the market for smart thermostats may not be sustainable in the long run given the high cost structure and competitive pressures. Some firms may exit the market, while others may continue to innovate and differentiate their products to remain competitive.
Learn more about marginal revenue here: brainly.com/question/30345507
#SPJ11
question 4: a school group went to a carnival on a field trip. the function c(x) represents the amount of money spent in dollars, where x is the number of students. does a possible solution of (29.5, $212.50) make sense for this function? explain your answer.
Answers
Step-by-step explanation:
only limited sense.
first of all, directly it does not make any sense. we can only send integer number of students on a field trip. not half-persons.
therefore, 29.5 students for a single field trip calculation does not make sense.
but : we could want to use the same function to calculate or analyze the costs of multiple field trips by using things like mean values of students participating. there fractions as student numbers make sense.
v^2 = 46 , estimate for v≈

Answers
Answer:
v ≈ 6.8
Step-by-step explanation:
Step 1: Write equation
v² = 46
Step 2: Square root both sides
v = √46
Step 3: Evaluate
v = 6.78233
Step 4: Round
v ≈ 6.8
HELPPP FOR BRIANLEST!!!!

Answers
Answer:
12/17
Step-by-step explanation:
total number of marbles that are purple (11) plus the total number of marbles that are not small (15) minus the number of marbles that are both purple and not small (2)
11 + 15 - 2 = 24
over the total number of marbles (34)
24/34 simplifies to 12/17
answer 13/17
Step-by-step explanation:
you add all the numbers up in the table, which would be 34 and then add up the ones that are big and the ones that are purple, which would be 26 so 26/34 then you simplify.
so 26/34=13/17
What does variability mean in mean absolute deviation?.
Answers
The mean absolute deviation (MAD), a measure of variability, illustrates the typical distance between an observation's mean and its variation. MAD uses the data's original units to facilitate interpretation.
Greater values indicate a wider range of data points than the average. The term "variability" refers to how much a data collection varies from one constituent to another. Variability measures reflect the level and magnitude of change within the data collection.
The interquartile range and the mean average deviation are the two methods for calculating variability that are required by the requirements for sixth-grade pupils.
The majority of the data values are fairly near to the mean, as shown by a tiny mean absolute deviation. We can infer from a large mean absolute deviation that numerous data values are dispersed widely from the mean.
To learn more about absolute deviation
https://brainly.com/question/23556021
#SPJ4
Suppose the KittyCat brand of litter products manufactures 15 lb bags of litter. Lisa, a cat owner, believes that these bags contain less than 15 lb of litter. She collects data on a randomly selected sample of 70 KittyCat 15 lb litter bags and decides to use a hypothesis test to determine whether the mean weight is less than 15 lb. Lisa believes that the weight of all such bags of litter is normally distributed, but she does not know the population standard deviation. Which of the following hypothesis tests should Lisa use regarding her claim?
a. one-sample, right-tailed z-test for a mean
b. one-sample, right-tailed 1-test for a mean
c. one-sample, left-tailed t-test for a mean
d. one-sample, left-tailed z-test for a mean
e. one-sample, two-tailed t-tes for a mean
Answers
Considering that she does not know the population standard deviation, the hypothesis test that she should use is given by:
c. one-sample, left-tailed t-test for a mean.
What hypothesis test should she use?First, we consider that she does not know the population standard deviation, hence a t-test should be used instead of a z-test.
Then, we consider that she suspects that the mean weight is less than 15 lb, and less is associated with a left-tailed test, instead of a right-tailed(associated with more) or a two-tailed(associated with different).
Hence option c is correct.
More can be learned about an hypothesis test at https://brainly.com/question/26454209
- Show BOTH distribution and FOIL to find the product of (3x - 2)and(2x + 6).
Answers
Given the following question:
\((3x-2)\times(2x+6)\)Foil method:
\(\begin{gathered} (3x-2)\times(2x+6) \\ \mleft(3x-2\mright)\mleft(2x+6\mright)=3x\cdot\: 2x+3x\cdot\: 6-2\cdot\: 2x-2\cdot\: 6 \\ 3x\cdot\: 2x+3x\cdot\: 6-2\cdot\: 2x-2\cdot\: 6 \\ 3x\times2x=6x \\ 6\times2=12 \\ 6x+x=7x\times2=14x \\ =6x^2+14x-12 \end{gathered}\)Your answer using the foil method is 6x^2 + 14x - 12
I need please If you don't know the answer then don't answer will mark brainleyest if right

Answers
The function is nonlinear
Answer:
nonlinear
Step-by-step explanation:
The original cost of a shirt was £40. It was reduced to £32.80 in a sale.
Calculate the percentage decrease.
Answers
Answer:
18% decrease
Step-by-step explanation:
-Subtract the ending value from the starting value.
40.00 - 32.80 = 7.20
-Divide this number by the starting value.
7.20 / 40.00 = 0.18
-Multiply by 100 to find the percentage change
0.18 * 100 = 18% decrease
50 POINTS WILL GIVE BRAINLIEST. Sienna has $8 and is saving $3 per week. Jacob has $6 and is saving $4 per week. Which model represents the equation that can determine when Sienna will have the same amount of money as Jacob?


Answers
Answer:
The answer is C (the third one).
Step-by-step explanation:
Let \(x\) represent the amount of weeks.
Sienna has $8, and she saves $3 per week.
In other words, after \(x\) weeks, she will have \(3x+8\) dollars.
Similarly, Jacob has $6 and is saving $4 per week.
In other words, after \(x\) weeks, he will have \(4x+6\) dollars.
Choice C is the only one that represents this scenario:
(For Sienna:) three (green) \(x\) bars with eight \(1s\) equals
(For Jacob:) four (green) \(x\) bars with six \(1s\).
Choice C is correct.
Simplify to create an equivalent expression.
2 – 4(5p + 1)

Answers
Answer:
A. -20p - 2
General Formulas and Concepts:
Pre-Algebra
Distributive PropertyAlgebra I
Combining Like TermsStep-by-step explanation:
Step 1: Define
2 - 4(5p + 1)
Step 2: Simplify
Distribute -4: 2 - 20p - 4Combine like terms: -20p - 2Answer:
Step-by-step explanation:
Apply the distributive property
2-20p-4
Simplify expression
-20p-2
Answer choice A is correct
Rewrite the equation by completing the square.
x^2 + 2x – 48 = 0
Answers
Answer:
(x+1)^2 = 49
x = 6 x = -8
Step-by-step explanation:
x^2 + 2x – 48 = 0
Add 48 to each side
x^2 + 2x =48
Take the coefficient of x
2
Divide by 2
2/2=1
Square it
1^2 =1
x^2 + 2x +1=48+1
x^2 +2x+1 = 49
(x+1)^2 = 49
Take the square root of each side
sqrt((x+1)^2) =±sqrt( 49)
x+1 = ±7
Subtract 1 from each side
x+1-1 = -1 ±7
x = -1+7 x = -1 -7
x = 6 x = -8
Rewrite as a simplified fraction.
2.31= ?
But the.01 is repeating
Answers
Answer:
104/45
Step-by-step explanation:
(2.31 x 10) - 2.3/9 =
20.8/9
Which is
208/90
Simplified:
104/45
Hope this helps!