Find the amount of money Greta can afford to borrow using the banker's rule. Greta makes $34,000 annually. What is the amount that can be borrowed? I came up with $13,600?
Answers
The total amount of Greta's debt payments (including the proposed new loan) should not exceed $13,600.
What is Total cost?
Average total cost is referred to as the sum total of all production costs divided by the total quantity of output.
According to this rule, the maximum amount of debt payments (including the proposed new loan) should not exceed 40% of the borrower's gross income.
To apply the banker's rule to Greta's situation, we can calculate her maximum affordable debt payments as:
Maximum affordable debt payments = 40% of gross income
Maximum affordable debt payments = 0.4 x $34,000
Maximum affordable debt payments = $13,600
This means that the total amount of Greta's debt payments (including the proposed new loan) should not exceed $13,600.
To know more about Total cost visit,
https://brainly.com/question/29509552
#SPJ1
Related Questions
Find the solution using a tape diagram
H + 12 = 34
Answers

there are 7 different roads between town a and town b, four different roads between town b and town c, and two different roads between town a and town c. (a) (5 points) how many different routes are there from a to c all together? (b) (5 points) how many different routes are there from a to c and back (any road can be used once in each direction)? (c) (5 points) how many different routes are there from a to c and back in part (b) that visit b at least once? (d) (5 points) how many different routes are there from a to c and back in part (b) that do not use any road twice?
Answers
To find the total number of different routes from town A to town C, we can first find the number of different routes from A to B and then multiply it by the number of different routes from B to C. There are 7 different roads between A and B and 4 different roads between B and C. Therefore, the total number of different routes from A to C is 7 x 4 = 28.
(b) To find the total number of different routes from town A to town C and back, we can use the product rule. There are 28 different routes from A to C (as calculated in part a) and 28 different routes from C to A (since we can use any road once in each direction). Therefore, the total number of different routes from A to C and back is 28 x 28 = 784.
(c) To find the total number of different routes from town A to town C and back in part (b) that visit town B at least once, we can use the principle of inclusion-exclusion. There are 28 different routes from A to C and 28 different routes from C to A. However, we need to subtract the routes that do not visit B at all. To find this number, we can use the product rule again, since there are 5 different roads between A and C that do not go through B (2 from A to C and 3 from C to A). Therefore, the number of routes that do not visit B at all is 2 x 3 = 6. So, the total number of different routes from A to C and back in part (b) that visit B at least once is 28 x 28 - 6 = 784 - 6 = 778.
(d) To find the total number of different routes from town A to town C and back in part (b) that do not use any road twice, we can use the principle of permutations. Since we cannot use any road twice, we need to find the number of permutations of the roads. There are 7 roads between A and B, 4 roads between B and C, and 2 roads between A and C. Therefore, the total number of different routes from A to C and back in part (b) that do not use any road twice is 7P2 x 4P2 x 2P2 = 126 x 12 x 2 = 3024.
Know more about routes here;
https://brainly.com/question/31146964
#SPJ11
6. Write an equation for the line that passes through (-4,4) and (8,8) in point-slope
form, slope-intercept form and standard form.
Point-Slope Form:
Slope-Intercept Form:
Standard Form:
Help!!

Answers
Answer:
Point-slope form:
\(y-4=\displaystyle\frac{1}{3}(x+4)\)
\(y-8=m(x-8)\)
Slope-intercept form:
\(y=\displaystyle\frac{1}{3}x+\displaystyle\frac{16}{3}\)
Standard form:
\(-x+3y=16\)
Step-by-step explanation:
Hi there!
1) Point-slope form
Point-slope form: \(y-y_1=m(x-x_1)\) where \((x_1,y_1)\) is a point on the line and m is the slope
First, determine the slope:
\(m=\displaystyle\frac{y_2-y_1}{x_2-x_1}\) where two points on the line are \((x_1,y_1)\) and \((x_2,y_2)\)
Plug in the points (-4,4) and (8,8):
\(m=\displaystyle\frac{8-4}{8-(-4)}\\\\m=\displaystyle\frac{8-4}{8+4}\\\\m=\displaystyle\frac{4}{12}\\\\m=\displaystyle\frac{1}{3}\)
Therefore, the slope of the line is \(\displaystyle\frac{1}{3}\). Plug this into \(y-y_1=m(x-x_1)\):
\(y-y_1=\displaystyle\frac{1}{3}(x-x_1)\)
Now, for \((x_1,y_1)\), we can either plug in (-4,4) or (8,8):
\(y-4=\displaystyle\frac{1}{3}(x-(-4))\\\\y-4=\displaystyle\frac{1}{3}(x+4)\)
or
\(y-8=m(x-8)\)
2) Slope-intercept form
Slope-intercept form: \(y=mx+b\) where m is the slope and b is the y-intercept (the value of y when the line crosses the y-axis)
\(y=mx+b\)
Plug in the slope
\(y=\displaystyle\frac{1}{3}x+b\)
Now, to determine the y-intercept, plug in one of the points (-4,4) or (8,8) and solve for b:
\(8=\displaystyle\frac{1}{3}(8)+b\\\\8=\displaystyle\frac{8}{3}+b\\\\8-\displaystyle\frac{8}{3}=b\\\\b=\frac{16}{3}\)
Therefore, the y-intercept is \(\displaystyle\frac{16}{3}\). Plug this back into \(y=\displaystyle\frac{1}{3}x+b\):
\(y=\displaystyle\frac{1}{3}x+\displaystyle\frac{16}{3}\)
3) Standard form
Standard form:
\(Ax+By=C\) where A, B, and C are numbers which are typically integers
\(y=\displaystyle\frac{1}{3}x+\displaystyle\frac{16}{3}\)
Organize this into standard form:
\(-\displaystyle\frac{1}{3}x+y=\displaystyle\frac{16}{3}\)
Multiply both sides by 3 so A, B, and C are integers:
\(-x+3y=16\)
I hope this helps!
Each lap around the track at Lincoln Community Center is 400 meters long. Levi ran a total of 1,600 meters as a warm-up before his workout. Let w be the number of laps Levi ran around the track as a warm-up. Write and solve an equation to find w.
Answers
To solve 400w = 1600, divide both sides by 400 to isolate the variable, and you will get w = 4.
3( 3v +5 ) = 39
Solve this problem
Answers
Answer:
V= 8/3
Step-by-step explanation:

Answer:
v = 8/3
Step-by-step explanation:
The goal here is to find the value of the variable, v, that makes this equation true. We go through a series of steps meant to isolate v on the left side and find the proper value to go on the right side. Here is one way of doing this:
Multiply, as indicated: 9v + 15 = 39.
Isolate 9v by subtracting 15 from both sides: 9v = 24.
Finally, divide both sides by 9 to obtain v = 8/3
An alternative approach follows:
Divide both sides of 3(3v + 5) = 39 by 3, obtaining 3v + 5 = 13.
Subtract 5 from both sides: 3v = 8
Divide both sides by 3: v = 8/3 (same as before)
one -third of a number is 12 less than the number itself
Answers
Answer:
4
Step-by-step explanation:
1/3x = x-12 thatsthe equation you use
mZS = 23
, arc RS = 86
, and RU is tangent to the circle at R. Find mZU.
S
U
Answers
Answer:
\(\angle U = 20^\circ\)
Step-by-step explanation:
Given
See attachment
\(\angle S = 23\)
arc \(RS = 86\)
Required
Find \(\angle U\)
Let
\(O \to\) center of the circle
We have that:
arc \(RS = 86\)
This implies that:
\(\angle SOR = 86^\circ\)
and
\(\triangle SOR \to\) is an isosceles triangle
because:
\(SO = OR \to\) the radius of the circle
And
\(\angle RSO = \angle ORS\)
So, we have:
\(\angle RSO + \angle ORS + \angle SOR = 180^\circ\) --- angles in a triangle
\(\angle RSO + \angle ORS + 86^\circ = 180^\circ\)
Collect like terms
\(\angle RSO + \angle ORS =- 86^\circ + 180^\circ\)
\(\angle RSO + \angle ORS =94^\circ\)
Recall that: \(\angle RSO = \angle ORS\)
So:
\(\angle RSO + \angle RSO =94^\circ\)
\(2\angle RSO =94^\circ\)
Divide by 2
\(\angle RSO =47^\circ\)
RU is a tangent.
So:
\(\angle ORU = 90^\circ\)
Given that:
\(\angle S = 23\)
Considering \(\triangle SRU\)
We have:
\(\angle RSU = \angle S = 23^\circ\)
So:
\(\angle SRU= \angle RSO + \angle ORU\)
\(\angle SRU= 47 + 90\)
\(\angle SRU= 137\)
Lastly:
\(\angle RUS + \angle RSU + \angle SRU =180^{0}\)
\(\angle RUS + 23 + 137=180^{0}\)
Collect like terms
\(\angle RUS =180^{0} - 23 - 137\)
\(\angle RUS =20^{0}\)
Hence:
\(\angle U = 20^\circ\)

In a four-workstation assembly line, the idle time for each table is 2,1,4,3 (in minute). What is the utilization rate of the line? a. Cannot be determined b. 10 minutes c. 6/16 d. 0.3
Answers
The answer is (a) Cannot be determined.
To calculate the utilization rate of the assembly line, we need to find the total time the workstations are busy and divide it by the total time available.
Given the idle times for each workstation as 2, 1, 4, and 3 minutes, respectively, the utilization rate can be calculated as follows:
Total idle time = 2 + 1 + 4 + 3 = 10 minutes
Total time available = Number of workstations × Time per workstation
= 4 workstations × Time per workstation (Assuming the same time per workstation)
= 4 × Time per workstation
Since the time per workstation is not given, we cannot determine the exact utilization rate.
Learn more about idle times, here
https://brainly.com/question/32470983
#SPJ11
A histogram contains a set of.......
Answers
Plz help I’ll give brainliest

Answers
1. y= -5
2. m=0
3. I dont know
1. 3x+4y=-20
x=0
3×0+4y=-20
0+4y=-20
y=-5
2. m=y/x
m=0/1
m= 0
3. Sorry
Solve each equation for the
1) g=C+a, for a
Answers
What is the name of the relationship between ∠1 and ∠8 ?
corresponding angles
alternate exterior angles
alternate interior angles
adjacent angles
Two parallel lines cut by a transversal. Angles are labeled one through four, starting above the top parallel line labeled 1 and 2 going left to right. Below the top parallel line labeling 3 and 4 going left to right. Angle 1 is acute. Angles are also labeled 5 through 8, starting above the bottom parallel line being labeled 5 and 6 going left to right. Below the bottom parallel line the angles are labeled 7 and 8 going from left to right.
Answers
Answer:
alternate exterior angles
Step-by-step explanation:
A graph titled Health Club Rates has a number of family members on the x-axis and Monthly cost (dollars) on the y-axis. For 2 family members, the cost is 84; 4 family members, 168; 6 family members, 252; 8 family members, 336.
Use the graph to find the unit rate.
$24 per person
$42 per person
$32 per person
$84 per person
Answers
Answer:
$42
Step-by-step explanation:
hope this helps
name the intersection of plane HEG and plain DFE

Answers
we conclude that the intersection of the planes HEG and DFE is the line FE
How to identify the intersection between the planes HEG and DFE?
Remember that the intersection of two planes is a line, so we just need to find a line that belongs to the two planes HEG (This plane would be the face that is behind the cube).
And the plane DFE is the right face of the shown cube.
Now, by looking at the given diagram, you can see that the line that belongs to two planes is the line EF (it is a common edge for the two faces that define the planes).
Then we conclude that the intersection of the planes HEG and DFE is the line FEIf you want to learn more about planes:
https://brainly.com/question/1655368
#SPJ1
What is the blank? _+6= -8
Answers
Answer:2+6=8 um hope these helped??
Step-by-step explanation:
If F: RS R' is a vector field whose component functions have continuous partial derivatives, and curl(F) = 0, then F is a conservative vector field: (Recall that 0 = (0,0.0))_
Answers
The last equation implies that F is a conservative vector field with the scalar potential f(x, y, z).
Suppose that F: RS R' is a vector field, and the component functions of F have continuous partial derivatives.
The curl of F is curl(F) = 0.
Then, F is a conservative vector field. (Recall that 0 = (0,0,0)).
To begin with, let F = (P, Q, R) be a vector field, which is a map from RS to R' defined by the following set of equations, F(x, y, z) = (P(x, y, z), Q(x, y, z), R(x, y, z)).
According to the given statement, the component functions of F have continuous partial derivatives.
Thus, the following equations hold:true
Partials of P exist and are continuous.true
Partials of Q exist and are continuous.true
Partials of R exist and are continuous.
Using the definition of the curl of F,
we have:curl(F) = (Ry - Qz, Px - Rz, Qx - Py)Since curl(F) = 0, it follows that:Ry - Qz = 0Px - Rz = 0Qx - Py = 0
We need to show that F is a conservative vector field. A vector field F is conservative if and only if it is the gradient of a scalar field, say f. In other words, F = grad(f) for some scalar function f.
Let us assume that F is conservative.
Then, we have:
F = grad(f) = (∂f/∂x, ∂f/∂y, ∂f/∂z)
By definition, curl(F) = (Ry - Qz, Px - Rz, Qx - Py).
Therefore, we can write:
Ry - Qz = (∂(Px)/∂z) - (∂(Qx)/∂y)Px - Rz = (∂(Qy)/∂x) - (∂(Py)/∂z)Qx - Py = (∂(Rz)/∂y) - (∂(Ry)/∂x)
Now, we can solve these equations for Px, Py,
and Pz:Pz = ∫(Ry - Qz)dx + g(y, z)Px = ∫(Qx - Py)dy + h(x, z)Py = ∫(Px - Rz)dz + k(x, y)Here, g(y, z), h(x, z), and k(x, y) are arbitrary functions of their respective variables, that is, they depend only on y and z, x and z, and x and y, respectively.
Since the component functions of F have continuous partial derivatives, we can use the theorem of Schwarz to show that Px = (∂f/∂x), Py = (∂f/∂y), and Pz = (∂f/∂z) are all continuous.
This means that g(y, z), h(x, z), and k(x, y) are all differentiable, and we can write:
g(y, z) = ∫(Ry - Qz)dx + C1(y)h(x, z) = ∫(Qx - Py)dy + C2(x)k(x, y) = ∫(Px - Rz)dz + C3(y)
Since we can take the partial derivative of f with respect to x, y, or z in any order, it follows that the mixed partial derivatives of g(y, z), h(x, z), and k(x, y) vanish.
Hence, they are all constant functions. Let C1(y) = C2(x) = C3(z) = C. Then, we have:
f(x, y, z) = ∫P(x, y, z)dx + C = ∫Q(x, y, z)dy + C = ∫R(x, y, z)dz + C
The last equation implies that F is a conservative vector field with the scalar potential f(x, y, z).
To know more about conservative vector, visit:
https://brainly.com/question/32064186
#SPJ11
There are 9 boys at a summer camp. The ratio
of boys to girls is 1 : 2. How many children are
at the summer camp in total?
Answers
Step-by-step explanation:
If the ratio of boys to girls is 1:2, then for every 1 boy there are 2 girls.
Let's use "x" to represent the number of girls at the summer camp.
So, if there are 9 boys, then the total number of children at the summer camp can be represented as:
9 boys + 2x girls = total number of children
But we don't know what "x" is yet. We can use the ratio to find out.
Since the ratio of boys to girls is 1:2, we know that the number of boys is one-third of the total number of children.
So, we can set up the following equation:
9 = (1/3) * total number of children
To solve for the total number of children, we can multiply both sides by 3:
27 = total number of children
Now we know that there are 27 children at the summer camp in total.
To find the number of girls, we can subtract the number of boys from the total number of children:
27 - 9 = 18
Therefore, there are 18 girls at the summer camp and a total of 27 children.
Answer:The problem involves working out the total number of children at a summer camp, given that there are nine boys and the ratio of boys to girls is 1:2. This problem can be solved using simple ratio and proportion, and basic arithmetic skills.To understand the problem, one needs to know that a ratio is a way of comparing numbers. In this case, the ratio of boys to girl is 1:2, which means that for every one boy, there are two girls.To work out the total children at the summer camp, we need to start by setting up an equation involving the ratio. Let “x” be the number of girls, and “y” be the total number of children in the camp. We know that the ratio of boys to girls is 1:2, so the number of girls is twice the number of boys, that is, x=2(9)=18.Next, we add the number of boys to the total number of children to get y: y = 9 + 18 = 27. Therefore, there are 27 children total at the summer camp.To verify this result, we can check that the ratio of boys to girls is 1:2, which is the same as 9:18. Dividing both sides by 9, we get 1:2, which means that we have worked out the correct answer.In summary, the total number of children at the summer camp is 27. The problem requires the use of ratios as a comparison of numbers, and the use of basic arithmetic skills to calculate the total number of children at the summer camp.
Step-by-step explanation:
The table and graph both represent the same relationship. Which
equation also represents that relationship?
у
12
у
х
0
0
10
2
4
8
4
8
6
6
12
4
N
02
4 6
y = 2x
y = x + 8
y = x + 2
y = x2
lol
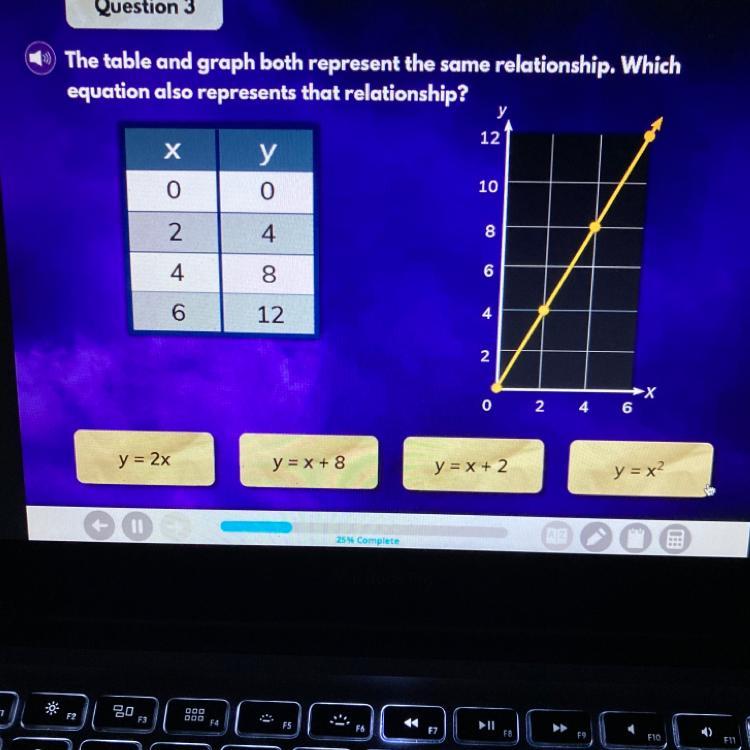
Answers
Answer:
Y=2x
Step-by-step explanation:
I did the iready quiz already:)
The equation of the proportional relationship represented by the table and the graph is: y = 2x.
What is a Proportional Relationship?If m is the slope or unit rate, a proportional relationship between two variables, x and y, can be represented with an equation as, y = mx.
Let's find the equation that represents the relationship represented by the graph and the table. Let's use the graph.
m = y/x
Using the point, (2, 4),
m = 4/2 = 2
Substitute m = 2 into y = mx
y = 2x
Therefore, the equation of the proportional relationship represented by the table and the graph is: y = 2x.
Learn more about proportional relationship on:
https://brainly.com/question/15618632
What is the value of 5/6+(-4/9)-(-2)
Answers
4/3 and 8/6 which is bigger.
"(help meeeee)"
Answers

what is five million four thousand three hundred in standard form
Answers
Answer:
5,400,300...........
5004300
........
......
....
...
..
.
Refer to the regular square pyramid shown. 13. B = ? 14. L.A. = ? 15. T.A. = ? 16. V = ?

Answers
The total surface area of the pyramid is 1,296 unit².
The lateral surface area (L.A) of the pyramid is 19.21 unit².
The volume of pyramid is 120 unit³.
What is the surface area of the pyramid?The surface area of the pyramid is calculated as follows;
T.S.A = 2bh + b²
where;
b is the base of the triangular faceh is the height of each triangular faceIn then diagram, we where given, base, b = 24 units, height = 15 units, then the surface area of the pyramid is calculated as follows;
T.S.A = 2 x 24 x 15 + 24²
T.S.A = 1,296 unit²
The lateral surface area is calculated as
L.A = √(b²/4 + h²)
L.A = √(24²/4 + 15²)
L.A = 19.21 unit²
The volume of pyramid is calculated as;
V = ¹/₃BH
V = ¹/₃ x 24 x 15
V = 120 unit³
Learn more about volume of pyramid here: https://brainly.com/question/18994842
#SPJ1
Classify the sequence {an) = {10,4,8/5,16/25,...} as arithmetic, geometric, or neither. If there is not enough information to classify the sequence, chose not enough information.
-
-
-
A. arithmetic
B. geometric
C. neither
D. not enough information
Answers
It is a geometric series.
The ratio of the second to first term is= \(\frac{4}{10}=\frac{2}{5}\)
The ratio of the third to second term is= \(\frac{\left(\frac{8}{5}\right)}{4}=\frac{2}{5}\)
The ratio of the fourth to third term is=\(\frac{\left(\frac{16}{25}\right)}{\left(\frac{8}{5}\right)}=\frac{2}{5}\)
Since the common ratios are same so it is a geometric series.
Learn more: https://brainly.com/question/8806877
g suppose 50 students took an exam and the average score was 70 with a standard deviation of 10. use 68-95-99.7 rule for questions dealing with normal distribution. if the distribution of scores is perfectly normal, how many students would you expect to get an a? (a score between 90 and 100) round up to nearest whole number.
Answers
Only one student is expected receive an A for the exam.
The 68-95-99.7 rule states that for a normal distribution, 68% of the data falls within one standard deviation of the mean, 95% of the data falls within two standard deviations of the mean, and 99.7% of the data falls within three standard deviations of the mean.
In this case, the mean is 70 and the standard deviation is 10, so the range of scores that would be considered an "A" would be between 90 and 100.
We can calculate the number of standard deviations from the mean that the range 90 to 100 covers and use the 68-95-99.7 rule to estimate the percentage of students who would receive an "A".
For a score of 90, the number of standard deviations from the mean is (90 - 70) / 10 = 2.
For a score of 100, the number of standard deviations from the mean is (100 - 70) / 10 = 3.
So, the range of scores between 50 and 90 covers two standard deviations from the mean and between 40 and 100 covers three standard deviations from the mean. According to the 68-95-99.7 rule, 99.7% of the data falls within three standard deviations of the mean and 95% of the data falls within two standard deviations of the mean, so we would expect about (99.7% - 95%)/2 = 2.35% of the students to receive an "A".
With 50 students, we would expect approximately 50 * 0.0235 = 1.175 ≈ ` student to receive an "A". We can round up to the nearest whole number to get an estimate of 50 students.
To know more on 68-95-99.7 rule
https://brainly.com/question/29255280
#SPJ4
Find all the complex roots. Write the answer in exponential
form. The complex fourth roots of 3−33i. Z0= z1= z2= z3=
Answers
The complex fourth roots of 3−33i are: \(z_0\) = 3.062\(e^{(-21.603)}\), \(z_1\) = 1.513\(e^{(22.247)}\), \(z_2\) = 0.3826\(e^{(22.247)}\) and \(z_3\) = 1.198\(e^{(76.247)}\).
To find the complex fourth roots of 3-33i, we can use the polar form of the complex number:
3-33i = 33∠(-86.41)
Then, the nth roots of this complex number are given by:
\(z_k\) = \(33^{(1/n)}\) × ∠((-86.41 + 360k)/n) for k = 0, 1, 2, ..., n-1
For n = 4, we have:
\(z_0\) = \(33^{(1/4)}\) × ∠(-86.41/4) ≈ 3.062∠(-21.603°)
\(z_1\) = \(33^{(1/4)}\) × ∠(88.99/4) ≈ 1.513∠(22.247°)
\(z_2\) = \(33^{(1/4)}\) × ∠(196.99/4) ≈ 0.3826∠(49.247°)
\(z_3\) = \(33^{(1/4)}\) × ∠(304.99/4) ≈ 1.198∠(76.247)
So the complex fourth roots of 3-33i are approximate:
\(z_0\) = 3.062\(e^{(-21.603)}\)
\(z_1\) = 1.513\(e^{(22.247)}\)
\(z_2\) = 0.3826\(e^{(22.247)}\)
\(z_3\) = 1.198\(e^{(76.247)}\)
Learn more about the complex roots at
https://brainly.com/question/5498922
#SPJ4
5. Write an equation in point-slope form for the line through the given point with the given slope.
(10,-9); m -2
ay-10-2(x+9)
b. y-9--2(x + 10)
c. y-9-2(x - 10)
y+9-2(x 10)
d.
Answers
Answer:
y + 9 = -2(x - 10)
The correct answer is d.
{y = 1/4x + 3 {y = 2x + 10 What is the solution for this system of equations?
Answers
The solution is:
A. (–8, 2), is the solution to the system of equations y=1/2x+6 and
y=3/4x-4
Here, we have,
(1) y = ½x + 6
(2) y = -¾x – 4 Set (1) = (2)
½x + 6 = -¾x – 4 Multiply each side by 4
2x + 24 = -3x – 16 Add 16 to each side
2x + 40 = -3x Subtract 2x from each side
40 = -5x Divide each side by -5
(3) x = -8 Substitute (2) into (1)
y = ½(-8) +6
= -4 + 6
= 2
The solution to the system of equations is (-8 ,2).
You can see the graphs of the two functions in the figure below. The two lines intersect at (-8, 2).
Check:
2 = ½(-8) + 6 2 = -¾(-8) - 4
2 = -4 +6 2 = 6 - 4
2 = 2 2 = 2
To learn more on equation click:
brainly.com/question/24169758
#SPJ1
complete question:
What is the solution to the system of equations below?
y=1/2x+6 and y=3/4x-4
A. (–8, 2)
B. (–8, –1)
C. (8, 10)
D. (8, –10)
Find the area of the shaded polygons
PLS HELP ASAP!!

Answers
Answer:
4.5
Step-by-step explanation:
I do RSM
k as the constant of variation for r varies directly as the square root of n and inversely as the square of y
Answers
The constant of variation k for this relationship is 4.
To find the constant of variation k for the given relationship, we can use the formula for direct and inverse variation:
k = (r * y^2) / √n
Where r is the variable that varies directly as the square root of n, and inversely as the square of y. To find the value of k, we can plug in the values of r, y, and n into the equation and solve for k.
For example, if r = 4, y = 2, and n = 16, we can plug these values into the equation to find k:
k = (4 * 2^2) / √16
k = (4 * 4) / 4
k = 16 / 4
k = 4
Therefore, the constant of variation k for this relationship is 4.
To know more about Variations:
https://brainly.com/question/23285852
#SPJ11
In an investigation on accuracy and precision, Myriah measures the mass of a 10. 00 g piece of metal several times. Her measurements are 9. 98 g, 10. 02 g, 10. 01 g, and 9. 99 g. Which statement best describes her results? They are both precise and accurate. They are neither accurate nor precise. They are precise but not accurate. They are accurate but not precise.
Answers
In an investigation on accuracy and precision, Myriah measures the mass of a 10. 00 g piece of metal several times. Her measurements are 9. 98 g, 10. 02 g, 10. 01 g, and 9. 99 g. The statement that best describes Myriah's results is that they are precise but not accurate.
Accuracy refers to how close a measured value is to the true or accepted value. Precision refers to the degree of agreement among repeated measurements. The mean of her measurements is: (9.98 g + 10.02 g + 10.01 g + 9.99 g) / 4 = 9.25 g. The results are precise because they are close together, and the mean value was calculated to the nearest hundredth of a gram. The measurements, on the other hand, were not accurate because they were all significantly less than the true value of 10.00 g.
To find the measure of angle A, place the protractor so that the base of the angle is aligned with the bottom line of the protractor. Then, read the measurement where the other side of the angle intersects the protractor. In this case, angle A intersects the protractor at 45 degrees. To find the measure of angle B, place the protractor so that the base of the angle is aligned with the bottom line of the protractor. Then, read the measurement where the other side of the angle intersects the protractor. In this case, angle B intersects the protractor at 120 degrees. Therefore, the measure of angle A is 45 degrees, while the measure of angle B is 120 degrees.
To know more about measures visit:
https://brainly.com/question/2384956
#SPJ11