Answers
Answer:
D) 1,020 square units
Step-by-step explanation:
36x48=1728
24x32=768
6x10=60
1728-768+60=1020 square units
Related Questions
HELP PLEASE
Select the equivalent expression.

Answers
Answer:c
Step-by-step explanation:
Answer:
C
Step-by-step explanation:
Express with positive exponent:
(6^2/z^4)^3
Evaluate:
6^6/z^12
a(n) ? is a shorthand method for writing a mathematical rule.a. equal sign (=)b. equationc. formulad. math problem
Answers
The equation is a shorthand method for writing a mathematical rule.
The answer to your question is b.equation. An equation is a shorthand method for writing a mathematical rule. It represents a relationship between two or more variables using mathematical symbols and operations. Equations are commonly used in algebra, calculus, and other areas of mathematics to solve problems and make predictions. They are written using an equal sign (=) to show that the expression on the left is equal to the expression on the right. Equations are an important tool in mathematics because they allow us to express complex ideas in a concise and precise way. By using equations, we can simplify calculations and solve problems more efficiently.
Visit here to learn more about the mathematical rule:
brainly.com/question/15502489
#SPJ11
Consider the piecewise function below f(x) = ( A cos x + 2, if x < 0 Be3x + Ax2 , if x ≥ 0. (a) For what value(s) of A and B is the above function continuous on (−[infinity],[infinity])? (b) Find the values of A and B such that the above function is differentiable
Answers
The value of A that makes the function a continuous function on (−∞, ∞) is A = -1. However, there are no values of A and B that make the function differentiable at x = 0.
To determine the values of A and B that make the given piecewise function continuous on the interval (−∞, ∞), we need to evaluate the conditions at the point where the two pieces of the function meet, which is x = 0.
(a) For the function to be a continuous function at x = 0, the limit of f(x) as x approaches 0 from the left (x < 0) must be equal to the limit of f(x) as x approaches 0 from the right (x ≥ 0). In other words, the left-hand and right-hand limits of the function should be equal at x = 0.
Let's evaluate the left-hand limit first:
lim(x→0-) f(x) = lim(x→0-) (A cos x + 2) = A cos(0) + 2 = A + 2.
Now, let's evaluate the right-hand limit:
lim(x→0+) f(x) = lim(x→0+) (\(e^{(3x)}\) + Ax²) = e⁰ + A(0)² = 1.
To ensure continuity, we set A + 2 = 1 and solve for A:
A + 2 = 1
A = -1.
Therefore, the value of A that makes the function continuous on (−∞, ∞) is A = -1. The value of B is not relevant to the continuity of the function since it does not appear in the definition.
(b) To find the values of A and B such that the function is differentiable, we need to check if the derivatives of the two pieces of the function match at x = 0.
Differentiating the left-hand piece, we have:
f'(x) = d/dx(A cos x + 2) = -A sin x.
Differentiating the right-hand piece, we have:
f'(x) = d/dx(\(e^{(3x)}\) + Ax²) = 3\(e^{(3x)}\) + 2Ax.
For the function to be differentiable at x = 0, the derivatives from the left and right must be equal.
Let's evaluate the derivatives at x = 0:
f'(0-) = -A sin(0) = 0,
f'(0+) = \(3e^{(3(0))} + 2A(0)\) = 3 + 0 = 3.
To ensure differentiability, we set -A sin(0) = 3 and solve for A:
-A sin(0) = 3,
0 = 3.
Since the equation is not satisfied, there are no values of A and B that make the function differentiable at x = 0.
Learn more about continuous function:
https://brainly.com/question/18102431
#SPJ11
data from central hudson labs determined the mean number of insect fragments in 225-gram chocolate bars was 14.4, but three brands had insect contamination more than twice the average. assume the number of fragments (contaminants) follows a poisson distribution. (a) if you consume a 225-gram bar from a brand at the mean contamination level, what is the probability of no insect contaminants?
Answers
The probability of finding 0 contaminated pieces in 225 g of chocolate is 5.57 X 10⁻⁷.
Here the number of contaminated fragments follows a Poisson process. Hence, let the distribution for the same be X.
Hence we get X ~ Poi(λt)
where λ is the mean no. of contaminated pieces and t is the no. of bars consumed.
For P(X = x) we get [(λt)ˣ e^(-λt)]/x!
Here λ = 14.4 and t = 1 Hence we will get
P(X = x) = [(14.4)ˣ e⁻¹⁴°⁴]/x!
Here we need to find the probability of the no. of contaminated pieces = 0
Therefore
P(X = 0) = [(14.4)⁰ e⁻¹⁴°⁴]/0!
Hence the probability of finding 0 contaminated pieces in a bar of chocolate is
P(X = 0) = e⁻¹⁴°⁴
= 5.57 X 10⁻⁷
know more about probability click here;
https://brainly.com/question/30060906
#SPJ4
what value of x is in the solution set of 9(2x + 1) < 9x - 18?
Answers
Answer:
x = -3
Step-by-step explanation:
9(2x + 1) < 9x -18
= 18x +9 < 9x - 18
= 18x -9x < -18 -9
= 9x = - 27
x = - 27/9
x= - 3
(r, 3), (5, 9), m=2 what is the answer
Answers
The value of the unknown variable in the ordered pair is 8
How to determine the value of the unknown variable in the ordered pair?From the question, we have the following ordered pairs that can be used in our computation:
(r, 3), (5, 9)
Also, we have
m = 2
The meaning of the above notations are
Ordered pairs (x, y) = (r, 3), (5, 9)
Slope, m = 2
The slope of points is calculated using the following slope equation
Slope, m = (y₂ - y₁)/(x₂ - x₁)
Where
(x, y) = (r, 3), (5, 9) and m = 2
Substitute the known values in the above equation, so, we have the following representation
(9 - 3)/(r - 5) = 2
Evaluate the difference
This gives
6/(r - 5) = 2
Divide both sides by 2
So, we have
3/(r - 5) = 1
Cross multiply
r - 5 = 3
So, we have
r = 3 + 5
Evaluate the sum
r = 8
Hence, the value of r is 8
Read more about slopes at
https://brainly.com/question/27630604
#SPJ1
Possible question
What is the value of r using the following points and slope
(r, 3), (5, 9), m=2
Stefa's family driving across the country. They have already traveled 1700 miles of the 2200 trip.how much farther do they need to go?
Answers
Answer:
2200-1700=500
Step-by-step explanation:
Parallel lines p and q are cut by transversal r. On line p where it intersects with line r, 4 angles are created. Labeled clockwise, from the uppercase left, the angles are: 1, 2, 4, 3. On line q where it intersects with line r, 4 angles are created. Labeled clockwise, from the uppercase left, the angles are: 5, 6, 8, 7. m∠3 is (3x + 4)° and m∠5 is (2x + 11)°. Angles 3 and 5 are . The equation can be used to solve for x. m∠5 = °
Answers
Answer:
77 degrees
Step-by-step explanation:
The diagram is drawn and attached below.
m∠3= (3x + 4)°
m∠5 = (2x + 11)°
Angles 3 and 5 are co-interior angles and are therefore supplementary (add up to 180 degrees).
(3x + 4)°+(2x + 11)°=180°
5x+15=180
5x=180-15
5x=165
x=33
Therefore, the measure of angle 5
m∠5 = (2x + 11)°
= (2(33) + 11)°
=66+11
=77°
The measure of angle 5 is 77 degrees.

Given: In ΔBLU, LE ⟂ BU , and BL ≅ UL Prove: ΔBEL ≅ ΔUEL STATEMENT REASON 1. LE⟂ BU and BL ≅ UL 1. Given 2. LE ≅ LE 2. Reflexive Property 3. ΔBEL ≅ ΔUEL 3. _______________ Which of the following choices will complete the reasoning for statement #3? A SSA B AAA C HL D None of these choices are correct.

Answers
Answer:
I think it is C
Step-by-step explanation:
The air temperature is −6℃ at sunrise and rises 4℃ every hour for several hours. The air temperature after x hours after sunrise is represented by the function f(x)=4x-6. Use intercepts to graph the function and interpret the intercepts in context.
Answers
Answer:
Step-by-step explanation:
F(x)=4x-6
It will start at -6C and every hour we will be going up by 4

the spiking of a neuron can be modeled by the differential equation dθ dt = 1 −cosθ (1 cosθ)i,
Answers
To study the behavior of the neuron, one can analyze the solution of this differential equation or study its phase portrait to understand the different states and dynamics of the neuron's spiking activity.
The given differential equation represents the spiking behavior of a neuron. It can be written as:
dθ/dt = 1 - cos(θ)
This equation describes the rate of change of the membrane potential (θ) of the neuron over time (t). The right-hand side of the equation represents the input current to the neuron, which is influenced by the difference between the resting potential and the current potential.
The equation shows that the rate of change of θ with respect to time is proportional to 1 minus the cosine of θ. The cosine term represents the influence of the current potential on the spiking behavior of the neuron.
To know more about equation visit:
brainly.com/question/10724260
#SPJ11
How is p-value calculated with example?
Answers
To calculate the p-value, we have to follow the following steps:
First, identify the correct test statistic.Then, calculate the test statistic using the relevant properties of the sample.Specify the characteristics of the test statistic’s sampling distribution.Then, place test statistics in the sampling distribution to find the p-value.To calculate the p-value, we need
p = sample proportion
p' = assumed population proportion in the null hypothesis
n = sample size
Example
Given, n =40, σ = 32.17 and X = 105.37. calculate p-value.
σₓ = σ/ √n
σₓ = 32.17 / √40
= 5.0865
Now, by applying the test static formula, we get
t = (105.37 – 120) / 5.0865
t = -2.8762
Using the table, we find the value of P(t>-2.8762)
From the table, we get
P (t<-2.8762) = P(t>2.8762) = 0.003
If P(t>-2.8762) = 1- 0.003 = 0.997
P- value = 0.997 > 0.05
To learn more about the p-value from the given link
https://brainly.com/question/13786078
#SPJ4
Keisha makes individual servings of nuts by dividing 4 1/2 cups of nuts individual 3/8 cup servings. How many individual servings can Keisha make?
Answers
Taking the quotient between the total amount and the amount needed for each serving, we can see that she can make 12 servings.
How many individual servings can Keisha make?To see how many individual servings can Keisha make, we need to take the quotient between the total amount of nuts that she has and the amount that she needs for each serving.
The total amount she has is:
T = (4 + 1/2) cups.
Each serving needs:
S = (3/8) cups.
Taking the quotient we will get:
N = (4 + 1/2)/(3/8)
N = (4.5)/(3/8) = 12
She can make 12 individual servings.
Learn more about quotients at:
https://brainly.com/question/629998
#SPJ1
Answer:
3/8
Step-by-step explanation:
To solve this problem, we need to perform division. We can convert the mixed fraction 4 1/2 into an improper fraction: 4 1/2 = (4 x 2 + 1)/2 = 9/2. Then we can divide 9/2 by 3/8:
(9/2) ÷ (3/8) = (9/2) x (8/3) = 12
Therefore, Keisha can make 12 individual servings of nuts by dividing 4 1/2 cups of nuts into 3/8 cup servings.
Find the absolute maximum and absolute minimum values of f on the given interval.
f(x) = xe−x2/162,
[−5, 18]
Answers
The absolute maximum value is 4.5, which occurs at x = sqrt(81/2), and the absolute minimum value is -4.5, which occurs at x = -sqrt(81/2).
To find the absolute maximum and minimum values of the function f(x) = x * e^(-x²/162) on the interval [-5, 18], we need to evaluate the function at its critical points and endpoints.
Critical points:To find the critical points, we need to find where the derivative of the function is equal to zero or undefined.
f'(x) = e^(-x²/162) - (2x²/162) * e^(-x²/162)
Setting f'(x) equal to zero and solving for x:
e^(-x²/162) - (2x²/162) * e^(-x²/162) = 0
e^(-x²/162) * (1 - 2x²/162) = 0
Since e^(-x²/162) is always positive and nonzero, the critical points occur when 1 - 2x²/162 = 0.
1 - 2x²/162 = 0
2x²/162 = 1
x²/81 = 1/2
x = 81/2
x = ±\(\sqrt{\frac{81}{2} }\)
Therefore, the critical points are x = \(\sqrt{\frac{81}{2} }\) and x = -\(\sqrt{\frac{81}{2} }\).
Endpoints:We also need to evaluate the function at the endpoints of the interval [-5, 18], which are x = -5 and x = 18.
Now, let's evaluate the function at the critical points and endpoints:
f(-5) = -5 * e^((-5)/162)
f(\(\sqrt{\frac{81}{2} }\)) = \(\sqrt{\frac{81}{2} }\) * e^(\(\sqrt{\frac{81}{2} }\))²/162)
f(-\(\sqrt{\frac{81}{2} }\)) = -\(\sqrt{\frac{81}{2} }\) * e^((-\(\sqrt{\frac{81}{2} }\))²)/162)
f(18) = 18 * e^((18²)/162)
To determine the absolute maximum and absolute minimum values, we compare the function values at these points:
f(-5) = -0.144
f(\(\sqrt{\frac{81}{2} }\)) =4.5
f(-\(\sqrt{\frac{81}{2} }\))) = -4.5
f(18) = 0.144
The absolute maximum value is approximately 4.5, which occurs at x = \(\sqrt{\frac{81}{2} }\), and the absolute minimum value is approximately -4.5, which occurs at x = -\(\sqrt{\frac{81}{2} }\).
Therefore, on the interval [-5, 18], the absolute maximum value of f(x) is approximately 4.5, and the absolute minimum value is approximately -4.5.
To learn more about absolute maximum: https://brainly.com/question/29589773
#SPJ11
Write the equation of a line that passes through the point (22,6) and is parallel to the line that passes through the points (0,24) and (3,2)
Answers
Answer:
Step-by-step explanation:
Find the distance between the given points: (-7, 5) and (-8, 4)
Find the distance between the given points: (-7, 5) and (-8, 4)
In a triangle ABC, a= 3 cm, b= 4 cm, c = 5 vm. Find the area of the triangle.
Answers
we can use Heron's formula to find the area of the triangle. The area of the triangle is 6 square centimeters.
To find the area of a triangle given its side lengths, we can use Heron's formula. Heron's formula states that the area of a triangle with side lengths a, b, and c is given by the formula:
Area = √(s(s-a)(s-b)(s-c))
where s is the semi-perimeter of the triangle, calculated as:
s = (a + b + c) / 2
In this case, the side lengths of the triangle are a = 3 cm, b = 4 cm, and c = 5 cm. We can calculate the semi-perimeter as:
s = (3 + 4 + 5) / 2 = 6 cm
Now, we can substitute the values of s, a, b, and c into Heron's formula:
Area = √(6(6-3)(6-4)(6-5))
= √(6(3)(2)(1))
= √(36)
= 6 cm²
Therefore, the area of the triangle is 6 square centimeters.
Learn more about Heron's formula here:
https://brainly.com/question/15188806
#SPJ11
3. Bridget is reviewing a nutrition label. She
wants to find the difference between the
amount of grams of saturated fat and
protein. How many more grams are there of
saturated fat than protein? Draw decimal
models to find the difference.
Answers
The difference between the amount of saturated fat and protein can be calculated using the subtraction operation. Hence, the difference is 0.59 grams.
Given the Parameters :
Grams of Saturated Fat = 1.08 grams Grams of protein = 0.49 gramsUsing the subtraction operation :
Grams of Saturated Fat - Grams of Protein 1.08 g - 0.49 g = 0.59 gramsHence, the amount of saturated fat is 0.59 grams more than Protein.
Learn more : https://brainly.com/question/25606306
what's the solution to the equation x/3 + x/6 = 7/2
Answers
Step-by-step explanation:
x/3+x/6=7/2
We simplify the equation to the form, which is simple to understand
x/3+x/6=7/2
Simplifying:
+ 0.333333333333x+x/6=7/2
Simplifying:
+ 0.333333333333x + 0.166666666667x=7/2
Simplifying:
+ 0.333333333333x + 0.166666666667x=+3.5
We move all terms containing x to the left and all other terms to the right.
+ 0.333333333333x + 0.166666666667x=+3.5
We simplify left and right side of the equation.
+ 0.5x=+3.5
We divide both sides of the equation by 0.5 to get x.
x=7
take l.c .m of 3 and 6 then
2x+x/6 = 7/2
3x = 7/2*3
x = 21/2/3
x = 21/2 * 1/3
x = 7/2
The volume, V, of a cylinder is V='h, wherer is the
radius of the cylinder and h is the height. Using rounding
to the nearest whole number, which of the following is an
estimate of the volume of a cylinder with a radius of
3.75 inches and height of 6.21 inches?
OA) 145 in.
OB) 180 in.
C) 288 in?
OD) 290 in.
Answers
The volume of the cylinder to the nearest whole number is 274 cubic inches
The formula for calculating the volume of a cylinder is expressed as:
V = πr²h
r is the radius = 3.75inh is the height = 6.21inSubstitute the given parameters:
V = 3.14 * 3.75² * 6.21
V = 274.21
Hence the volume of the cylinder to the nearest whole number is 274 cubic inches
Learn more on volume of a cylinder here: https://brainly.com/question/9554871
A bouncy ball is dropped such that the height of its first bounce is 4.5 feet and each successive bounce is 73% of the previous bounce's height. What would be the height of the 10th bounce of the ball? Round to the nearest tenth (if necessary).
Answers
The height of the 10th bounce of the ball will be 0.6 feet.
What is geometric sequence?A geometric sequence is a sequence in which each term is found by multiplying the preceding term by the same value.
What is the formula for finding the nth term of geometric sequence?The nth term of the geometric sequence is given by
\(\sf T_n=ar^{n-1}\)
Where,
\(\sf T_n\) is the nth term.r is the common ratioa is the first termAccording to the given question.
During the first bounce, height of the ball from the ground, a = 4.5 feet
And, the each successive bounce is 73% of the previous bounce's height.
So,
During the second bounce, the height of ball from the ground
\(\sf = 73\% \ of \ 10\)
\(=\dfrac{73}{100}(10)\)
\(\sf = 0.73 \times 10\)
\(\sf = 7.3 \ feet\)
During the third bounce, the height of ball from the ground
\(\sf = 73\% \ of \ 7.3\)
\(=\dfrac{73}{100}(7.3)\)
\(\sf = 5.33 \ feet\)
Like this we will obtain a geometric sequence 7.3, 5.33, 3.11, 2.23,...
And the common ratio of the geometric sequence is 0.73
Therefore,
The sixth term of the geometric sequence is given by
\(\sf T_{10}=10(0.73)^{10-1\)
\(\sf T_{10}=10(0.73)^{9\)
\(\sf T_{10}=10(0.059)\)
\(\sf T_{10}=0.59\thickapprox0.6 \ feet\)
Hence, the height of the 10th bounce of the ball will be 0.6 feet.
Find out more information about geometric sequence here:
brainly.com/question/11266123
A custotuer requires during the next four months respectively 50,65,100, and 70 units of a commodity (no backlogs wllowed). Productions costs are $5,$8,$4, and $7 per unit during these months. The storage cost from one month to the next are $2 per unit (assessed on the end of the month inventory). Each unit at the end of the month 4 could be sold for $15 /unit. The production capacities for each month are 90, 75, 80 , and 50 units respectively. Currently, there are 15 units in inventory. Formulate a Linear Program that will minimize the objective function (sum of the production and inventory costs - revenue from selling end of period inventory at month 4). Note, inventory cost is assessed only for the first 3 periods. Model and solve the problem in AMPL and answer the quiz.
Answers
The formulated Linear Program aims to minimize the objective function, which is the sum of production and inventory costs minus the revenue from selling the end-of-period inventory at month 4.
In this problem, we need to determine the optimal production and inventory levels over the four-month period to minimize costs and maximize revenue. We can formulate this as a linear programming problem with the following decision variables:
Let x1, x2, x3, x4 represent the production quantities for months 1, 2, 3, and 4, respectively.
Let y1, y2, y3, y4 represent the end-of-month inventory levels for months 1, 2, 3, and 4, respectively.
The objective function we want to minimize is:
Minimize: (5x1 + 8x2 + 4x3 + 7x4) + (2y1 + 2y2 + 2y3) - (15y4)
Subject to the following constraints:
1. Initial inventory: y1 = 15 (given)
2. Production capacity constraints:
x1 <= 90 (month 1 capacity)
x2 <= 75 (month 2 capacity)
x3 <= 80 (month 3 capacity)
x4 <= 50 (month 4 capacity)
3. Inventory balance equations:
y1 + x1 - 50 = y2 (month 1)
y2 + x2 - 65 = y3 (month 2)
y3 + x3 - 100 = y4 (month 3)
y4 + x4 - 70 = 0 (month 4, no carryover inventory)
4. Non-negativity constraints:
x1, x2, x3, x4, y1, y2, y3, y4 ≥ 0
Learn more about Linear Program
brainly.com/question/32090294
#SPJ11
You wish to test the following claim (H) at a significance level of a = a = 0.01.
Hoμ64.9 Η μ < 64.9
You believe the population is normally distributed, but you do not know the standard deviation. You obtain a sample of size n = 17 with mean M= 59.7 and a standard deviation of SD = 6.3.
What is the p-value for this sample? (Report answer accurate to four decimal places.) p-value=
The p-value is...
less than (or equal to) a
greater than a
This p-value leads to a decision to...
reject the null
accept the null
fail to reject the null
As such, the final conclusion is that...
There is sufficient evidence to warrant rejection of the claim that the population mean is less than 64.9.
There is not sufficient evidence to warrant rejection of the claim that the population mean is less than 64.9.
The sample data support the claim that the population mean is less than 64.9.
There is not sufficient sample evidence to support the claim that the population mean is less than 64.9.
Answers
The p-value from the appropriate resources to determine the final conclusion in this case.
To determine the p-value for the given sample, we need to perform a one-sample t-test.
Given:
Null hypothesis (H₀): μ = 64.9
Alternative hypothesis (H₁): μ < 64.9
Sample mean (M) = 59.7
Sample standard deviation (SD) = 6.3
Sample size (n) = 17
Significance level (α) = 0.01
To calculate the p-value, we can use the t-distribution and the test statistic formula:
t = (M - μ) / (SD / √n)
Substituting the given values, we get:
t = (59.7 - 64.9) / (6.3 / √17)
Now we can calculate the test statistic:
t = -5.2 / (6.3 / √17)
Next, we can calculate the degrees of freedom (df) using the sample size (n - 1):
df = 17 - 1 = 16
Using the t-distribution table or a statistical software, we can find the p-value corresponding to the calculated test statistic and degrees of freedom.
However, since the p-value is not provided in the question, I cannot provide the exact value. You would need to consult a t-distribution table or use statistical software to obtain the p-value.
Once you have the p-value, compare it to the significance level (α = 0.01) to make a decision:
If the p-value is less than or equal to α, reject the null hypothesis.
If the p-value is greater than α, fail to reject the null hypothesis.
Finally, based on the decision made, you can draw a conclusion:
If the null hypothesis is rejected, the conclusion would be: "There is sufficient evidence to warrant rejection of the claim that the population mean is less than 64.9."
If the null hypothesis is not rejected, the conclusion would be: "There is not sufficient evidence to warrant rejection of the claim that the population mean is less than 64.9."
Please obtain the p-value from the appropriate resources to determine the final conclusion in this case.
Learn more about Hypothesis testing.
brainly.com/question/17099835
#SPJ11
Please help- pls pls
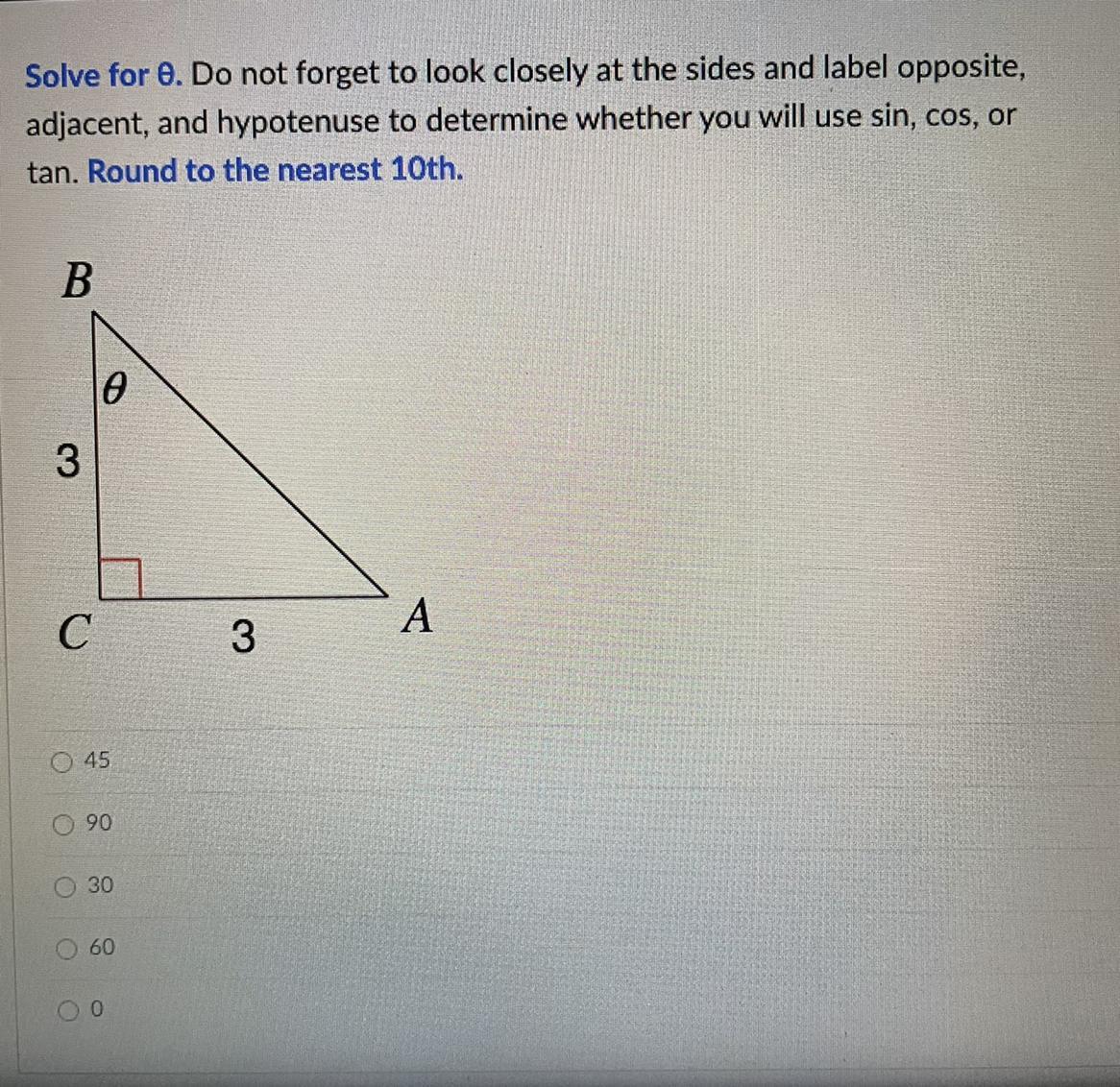
Answers
Answer:
45⁰
Step-by-step explanation:
use TanB=(3/3)
B=Tan-¹(3/3)
B=45⁰
Solve the inequality -12 ≤ 2x -4 < 10
Answers
Answer:
-4 ≤ x <7
x is greater than or equal to -4, and x is less than 7
Step-by-step explanation:
Take each side and solve
-12 ≤ 2x -4
subtract 4 on both sides
-8 ≤ 2x
divide by 2 on both sides
-4 ≤ x
2x -4 < 10
add 4 on both sides
2x < 14
divide by two on both sides
x < 7
Final answer:
-4 ≤ x <7
Answer:
-4 ≤ x < 7
Step-by-step explanation:
Method 1: Split the inequality into two parts,
-12 ≤ 2x-4
and
2x -4 < 10
Solve.
-8 ≤ 2x
2x ≥ -8
x ≥ -4
and
2x < 14
x < 7
So, x is greater than (or equal to) -4, but less than 7.
-4 ≤ x < 7
Method 2:
-12 ≤ 2x - 4 < 10
Add 4 to both sides.
-8 ≤ 2x < 14
Divide both sides by 2.
-4 ≤ x < 7
A factory produces 42,000 computer monitors per day. The manager of the factory claims that fewer than 660 defective computer monitors are produced each day. In a random sample of 240 computer monitors, there are 2 defective computer monitors. Determine whether the manager's claim is likely to be true. Explain.
Answers
Answer:
The manager's claim is likely to be true.Step-by-step explanation:
We are given that the factory produces 42,000 computer monitors per day
And the claim is of this amount produces fewer than 660 are defective.
a random sample shows that of 240 monitors 2 are defective
to verify the factory managers claim we need to know how many 240s are there in 42000
=42000/240= 175
Since each 240 will give 2 defective monitors
175 will give= 175*2= 350
350 is less than 660 hence the managers claim is correct
Find the value for x

Answers
Answer:
Value of x --> 15°
Step-by-step explanation:
(2x + 60°) and 6x lie on a straight line. So, they form a linear pair. Their sum gives 180°.
---> (2x + 60°) + 6x = 180°
2x + 60° + 6x = 180°
8x + 60° = 180°
8x = 180°- 60°
8x = 120
x = \(\frac{120}{8}\)
x equals 15°Devin volunteers at Big Pup Rescue. He is mixing up shampoo solution for the dog washing station. He needs 2 cups of shampoo concentrate for every 9 cups of water. Devin will use 36 cups of water.
How much shampoo concentrate should Devin add to the water to make the shampoo solution?
Answers
Answer:
8
Step-by-step explanation:
Make a ratio
2:9 = 11
In total there will be 11 cups of solution.
2:9 = 11
?:36 = ?
Divide
36 / 9 = 4
Now that you have found the scale factor, multiply
2 × 4 = 8
So, you will need 8 cups of shampoo concentrate.
A rectangle has area 36 m2. Express the perimeter of the rectangle as a function of the length (L) of one of its sides. P(L) =
Answers
Let's denote the length of one side of the rectangle as L and the width as W. Given that the area of the rectangle is 36 m², we have the equation:
Area = Length × Width
36 = L × W
To express the perimeter of the rectangle as a function of the length (L), we need to find the relationship between the length and the width.
Solving the equation for W, we get:
W = 36 / L
The perimeter (P) of the rectangle is given by the formula:
P = 2L + 2W
Substituting the value of W, we have:
P(L) = 2L + 2(36 / L)
Simplifying further:
P(L) = 2L + 72 / L
Therefore, the perimeter of the rectangle, expressed as a function of the length (L) of one of its sides, is given by P(L) = 2L + 72 / L.
Learn more about perimeter here:
https://brainly.com/question/7486523
#SPJ11
Let f be the function with f(0)=1/pi^2, f(2)=1/pi^2, and derivative given by f'(x)=(x+1)cos(pix).
How many values of x in the open interval (0,2) satisfy the condition of the MVT for the function f on the closed interval [0,2]?
Answers
There are at least two solutions to the equation (c + 1)cos(πc) = 1/π in the interval (0, 2), and the answer is (C) Two.
How to calculate the valuef'(c) = (f(2) - f(0))/(2 - 0)
f'(c) = 1/(π)
Substituting the given expression for f'(x) gives:
(c + 1)cos(πc) = 1/(π)
The graph of (c + 1)cos(πc) is a smooth, continuous curve that starts at (0, 1) and ends at (2, -1). The graph of 1/π is a horizontal line at y = 1/π.
Since the cosine function oscillates between -1 and 1, the graph of (c + 1)cos(πc) must cross the graph of 1/π at least twice in the interval (0, 2).
Learn more about equations on
https://brainly.com/question/2972832
#SPJ1
Let f be the function with f(0)=1π2,f(2)=1π2, and derivative given by f'(x)=(x+1)cos(πx). How many values of x in the open interval (0, 2) satisfy the conclusion of the Mean Value Theorem for the function f on the closed interval [0, 2] ?
A. None
B. One
C. Two
D. More than two
Solve the following: 6(x-2)>15
Answers
6(x-2) > 15
6x - 12 > 15
6x > 27
x > 27/6
Hope it helps!
Answer:
x>4.5
Step-by-step explanation:
6(x-2)>15
We do this is as if it were an equation:
6(x-2)>15
Expand the brackets:
6x-12>15
Add 12 to both sides:
6x-12+12>15+12
Simplify:
6x>37
Now we divide both sides by 6:
6x÷6>37÷6
x > 4.5
If we put 5 into the original equation as it is more than 4.5, we get:
6(5-2)>15
We can simplify the brackets or expand first:
Simplifying the brackets first:
6(3)>15
18>15 ✅
Expanding first:
6(5-2)>15
30-12>15
18>15 ✅
