Find the derivative of the following function. -7x + 6 y = 5
Answers
The derivative of the function -7x + 6y = 5 with respect to x is \(dy/dx = 7/6\).
How to find the derivative of -7x + 6y = 5?To find the derivative of -7x + 6y = 5, we need to solve for y in terms of x and then find the derivative of y with respect to x.
-7x + 6y = 5
Add 7x to both sides:
6y = 7x + 5
Divide both sides by 6:
y = (7/6)x + 5/6
Now, we can find the derivative of y with respect to x:
\(dy/dx = d/dx [(7/6)x + 5/6]\)
= (7/6) d/dx x + d/dx (5/6)
= 7/6
Therefore, the derivative of the function -7x + 6y = 5 with respect to x is \(dy/dx = 7/6\).
Learn more about derivative.
brainly.com/question/30365299
#SPJ11
Related Questions
PLEASE HELP ME OUT 12x^2+4x-1
Answers
(if im wrong then mb)
Answer:
(6x-1)(2x+1)
Step-by-step explanation:
12x²+4x-1 (find two numbers that when you add or subtract them the ANS will be the coefficient of x and those same numbers when you multiply them the ANS will be the product of 12 and -1) then replace the middle term with those numbers.
12x²+6x-2x-1
(12x²+6x)(-2x-1)
6x(2x+1)-1(2x+1)
(6x-1)(2x+1)
Osborne invested $17,000 in stocks and bonds.
If he made a 10% profit on his stocks and a
7% profit on his bonds, and the combined profit
was $1,280, how much did Osborne invest in
stocks?
Answers
S+B = 17000
0.1S+0.07B=1280
Multiply the first equation by 0.1 and subtract the second equation
0.03B=420
B=14,000
S=3,000
The amount that Osborne invested in stocks is $3000.
What are Linear Equations?Linear equations are equation involving one or more expressions including variables and constants and the variables are having no exponents or the exponent of the variable is 1.
Let x be the amount invested in stocks and y be the amount invested in bonds.
Combined investment = $17,000
x + y = 17000 [Equation 1]
Profit from stocks = 10% = 0.1x
Profit from bonds = 7% = 0.07y
Combined profit = $1280
0.1x + 0.07y = 1280 [Equation 2]
We get two linear equations.
Solving this gives the values of x and y.
Multiplying [Equation 1] by 0.1, we get,
0.1x + 0.1y = 1700 Equation 3]
Subtracting [Equation 2] from [Equation 3], we get,
0.1y - 0.07y = 1700 - 1280
0.03y = 420
y = 14,000
Substituting y in [Equation 1],
x = 17,000 - 14,000 = 3000
Hence the amount invested in stocks is $3000.
Learn more about Linear Equations here :
https://brainly.com/question/21835898
#SPJ2
A pair o dice is rolled and the resulting number is odd. Which of the following is
the complement of this event ?
a. A number greater than 8 is rolled b. A number less than 5 is rolled
C. An even number is rolled
d. A multiple of 5 is rolled
Answers
The query is about probability and complements. A pair of dice is rolled, and the outcome is interesting since the resultant number is odd. The aim is to identify whether the complement of this event is the event of rolling an even number or one of the other choices supplied.
An event's complement is the collection of outcomes that are not included in the event. As a result, the solution will be the set of outcomes that correspond to rolling an odd number on a pair of dice.
The alternatives are as follows: (a) a number larger than 8, (b) a number less than 5, (c) an even number, and (d) a multiple of 5.
Learn more about probability and complements:
https://brainly.com/question/13604758
#SPJ11
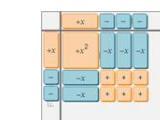
Which geometric model using algebra tiles represents the factorization of x2 – 5x 6? An algebra tile configuration. 4 tiles are in the Factor 1 spot: 1 is labeled x and 3 are labeled negative. 3 tiles are in the Factor 2 spot: 1 is labeled x and 2 are labeled negative. 12 tiles are in the Product spot: 1 is labeled x squared, 5 are labeled negative x, and 6 are labeled. An algebra tile configuration. 3 tiles are in the Factor 1 spot: 1 is labeled x and 2 are labeled negative. 3 tiles are in the Factor 2 spot: 1 is labeled x and 2 are labeled negative. 11 tiles are in the Product spot: 1 is labeled x squared, 4 are labeled negative x, and 6 are labeled. An algebra tile configuration. 3 tiles are in the Factor 1 spot: 1 is labeled x and 2 are labeled negative. 3 tiles are in the Factor 2 spot: 1 is labeled x and 2 are labeled negative. 11 tiles are in the Product spot: 1 is labeled x squared, 4 are labeled negative x, and 6 are labeled. An algebra tile configuration. 4 tiles are in the Factor 1 spot: 1 is labeled x and 3 are labeled negative. 4 tiles are in the Factor 2 spot: 1 is labeled x and 3 are labeled negative. 12 tiles are in the Product spot: 1 is labeled x squared, 5 are labeled negative x, and 6 are labeled.
Answers
The statement for geometric model using algebra tiles represents the factorization is the statement number 2.
What is algebra tile?Algebra tiles used to represent the algebraic expression in the table form. The shape of algebra tile is square and rectangle, in which the variables represented.
The given polynomial equation in the problem is,
\(x^2 -5x+6\)
In the above polynomial, the highest power of variable is 2. Thus, it is a quadratic equation.The image of the algebra tile for the given polynomial attached below.
The statement which satisfy the polynomial and its algebra tile is,
An algebra tile configuration.
3 tiles are in the Factor 1 spot: 1 is labeled x and 2 are labeled negative. 3 tiles are in the Factor 2 spot: 1 is labeled x and 2 are labeled negative.11 tiles are in the Product spot: 1 is labeled x squared, 4 are labeled negative x, and 6 are labeled.Thus, the statement for geometric model using algebra tiles represents the factorization is the statement number 2.
Learn more about the algebra tile here;
https://brainly.com/question/4407619
Answer: Graph two <3
Step-by-step explanation:
Determine the solution for the following equation: (8x-8)3/2=64
Answers
Answer:
X=3
Step-by-step explanation:
Edge2021
What is the value of X?

Answers
Answer:
x=20
Step-by-step explanation:
First, find LJ
Angle L = 60 (180 - 30 - 90)
The cosine of an angle is equal to the ratio of the adjacent side to the hypotenuse.
cos(L)=adj/hyp
cos(60)=LJ/40√2
LJ = cos(60)*40√2
LJ = 20√2
Now you can use LJ to find x. You also know the value of each angle, 45
x=20√2⋅cos(45)
x=20
if 60% is 27 what is 100%
Answers
x y
1 6
4 15
6 21
Which rule describes the relationship between the x- and y-coordinates in the following table?
Answers
Answer:
415
Step-by-step explanation:
4.15 ×
\(4.15 \: \times {10}^{2} \)
If the graph of an equation is symmetric with respect to the origin and (3,-4) is a point on the graph, then is also a point on the graph.
Answers
The graph is symmetric with respect to the origin, f(x,y) = f(–x,–y), so we can substitute to get g(\(x^2\) + \(y^2\)) = g(\(x^2\) + \(y^2\)), which is true for all x and y. Therefore, (–x,–y) is also on the graph.
If the graph of an equation is symmetric with respect to the origin and (3,-4) is a point on the graph, then (–3,4) is also a point on the graph.
The reason for this is that any point on a graph that is symmetric with respect to the origin can be reflected across the origin to produce another point that is also on the graph.
For example, suppose we have a graph that is symmetric with respect to the origin, and the point (3,-4) is on the graph. We can reflect this point across the origin to get the point (–3,4), which will also be on the graph.
This is because the x-coordinate of (3,-4) is positive and the y-coordinate is negative, so when we reflect it across the origin, the x-coordinate becomes negative and the y-coordinate becomes positive.
In general, if a graph is symmetric with respect to the origin, then for any point (x,y) on the graph, the point (–x,–y) will also be on the graph. This is because reflecting a point across the origin changes the sign of both the x-coordinate and the y-coordinate.
To prove this, we can use the fact that the equation of a graph that is symmetric with respect to the origin can be written in the form f(x,y) = g(x+y),
Where g is a function of one variable. If (x,y) is on the graph, then f(x,y) = g(\(x^2\) + \(y^2\)), and if we reflect this point across the origin to get the point (–x,–y), then the equation becomes f(–x,–y) = g(\(x^2\) + \(y^2\)).
For more related questions on symmetric:
https://brainly.com/question/14466363
#SPJ8
Given a normal distribution with μ=46 and σ=5, complete parts (a) through (d). Click here to view page 1 of the cumulative standardized normal distribution table. Click here to view page 2 of the cumulative standardized normal distribution table. a. What is the probability that X>37 ? P(X>37)= (Round to four decimal places as needed.) b. What is the probability that X<41 ? P(X<41)= (Round to four decimal places as needed.) c. For this distribution, 10% of the values are less than what X-value? X= (Round to the nearest integer as needed.) d. Between what two X-values (symmetrically distributed around the mean) are 60% of the values? For this distribution, 60% of the values are between X= and X= (Round to the nearest integer as needed.)
Answers
a.The probability that X > 37, P(X > 37) = 0.9641
b. P(X < 41) = 0.1587
c. X = 39
d. X = 42 and X = 50 (symmetrically distributed around the mean)
a. To find the probability that X > 37, we need to calculate the area under the normal distribution curve to the right of 37. Using the z-score formula:
z = (X - μ) / σ
where X is the given value, μ is the mean, and σ is the standard deviation, we can calculate the z-score:
z = (37 - 46) / 5 = -1.8
Using the cumulative standardized normal distribution table, we can find the corresponding probability. The table indicates that P(Z < -1.8) = 0.0359.
Since we are interested in P(X > 37), which is the complement of P(X ≤ 37), we subtract the obtained value from 1:
P(X > 37) = 1 - 0.0359 = 0.9641 (rounded to four decimal places)
b. To find the probability that X < 41, we calculate the z-score:
z = (41 - 46) / 5 = -1
From the cumulative standardized normal distribution table, we find that P(Z < -1) = 0.1587.
Therefore, P(X < 41) = 0.1587 (rounded to four decimal places).
c. To find the X-value for which 10% of the values are less, we need to find the corresponding z-score. From the cumulative standardized normal distribution table, we find that the z-score for a cumulative probability of 0.10 is approximately -1.28.
Using the formula for the z-score:
z = (X - μ) / σ
we rearrange it to solve for X:
X = μ + (z * σ)
X = 46 + (-1.28 * 5) ≈ 39 (rounded to the nearest integer)
Therefore, 10% of the values are less than X = 39.
d. To find the X-values between which 60% of the values are located, we need to determine the z-scores corresponding to the cumulative probabilities that bracket the 60% range.
Using the cumulative standardized normal distribution table, we find that a cumulative probability of 0.20 corresponds to a z-score of approximately -0.84, and a cumulative probability of 0.80 corresponds to a z-score of approximately 0.84.
Using the z-score formula:
X = μ + (z * σ)
X1 = 46 + (-0.84 * 5) ≈ 42 (rounded to the nearest integer)
X2 = 46 + (0.84 * 5) ≈ 50 (rounded to the nearest integer)
Therefore, 60% of the values are between X = 42 and X = 50.
Learn more about probability
brainly.com/question/31828911
#SPJ11
What is the equation of the absolute function shown in the graph

Answers
Answer is 6|x+2|+2
Please check the attached image of answer to clear the doubt.
By Benjemin ☺️

Can someone help me :)

Answers
Answer:
X = 2
Step-by-step explanation:
Since 21 divided by 7 is 3, then that means that x times 3 has to be 6. Since 2 times 3 is 6, X = 2
Answer:
x = 2
Step-by-step explanation:
21/6 divided by 3 on each side is 7/2.
Convert 110011 no decimal number System
Answers
(110011)2 = (51)10
Step by step solution
Step 1: Write down the binary number:
110011
Step 2: Multiply each digit of the binary number by the corresponding power of two:
1x25 + 1x24 + 0x23 + 0x22 + 1x21 + 1x20
Step 3: Solve the powers:
1x32 + 1x16 + 0x8 + 0x4 + 1x2 + 1x1 = 32 + 16 + 0 + 0 + 2 + 1
Step 4: Add up the numbers written above:
32 + 16 + 0 + 0 + 2 + 1 = 51.
So, 51 is the decimal equivalent of the binary number 110011.
during his nba career, larry bird made approximately 89% of all free throws. suppose larry makes 10 free throws in a row. what is the probability he will make the next free throw?
Answers
Probability that he will make the next free throw is 0.89% if larry bird made approximately 89% of all free throws during his nba career.
During nba career he made approximate 89% of all free throws.
To calculate the probability of the next 10 free throws given which will be
= No. of possible outcome / Total no. of outcome
= 89 / 100
= 0.89 %
Probability is simply how likely something is to happen. Whenever we're unsure about the outcome of an event, we can talk about the probabilities of certain outcome like how likely they are.
P(A) = (# of ways A can happen) / (Total number of outcomes)
which means that Probability that he will make the next free throw is 0.89 %
To learn more about probability
https://brainly.com/question/9653825
#SPJ4
What is (4c)^2d ?
c = 5 and d = 8
Answers
Answer:
3200
Step-by-step explanation:
Replace the variables with their values and do the arithmetic.
(4·5)²·8 = 20²·8 = 400·8 = 3200
A bakery sold a total of 200 cupcakes in a day, and 42 of them were chocolate flavored. What percentage of cupcakes sold that day were chocolate flavored?.
Answers
Percentage of cupcakes which was chocolate flavored = 21%. The formula to calculate percentage is (x/100 * total number of items = given no of items).
Let x be the percentage of chocolate flavored cupcakes
Therefore,
x% of 200 = 42
Since the total no. of cupcakes is 20.
=> x/100 * 200 = 42
=> x * 2 = 42
=> x =21
Hence the required percentage is 21 %.
A % is a number without dimensions. It is a ratio or a number that is written as a fraction of one hundred. The percentage sign (%) is the symbol used to represent a percentage. Pct and pc are two examples of the acronyms used. Typically, the relative amount of the entire number is expressed using the percentage.
To learn more about percentage
https://brainly.com/question/21590329
#SPJ4
What is the slope of this line?

Answers
Answer:
-3/2
Step-by-step explanation:
you can use the rise over run method to find the slope of this line
The AAA reports that the mean price per gallon of regular gasoline is $3.20, with a population standard deviation of $0.20. Assume a random sample of 16 gasoline stations is selected and their mean cost for regular gasoline is computed. What is the probability that the difference between the sample mean and the population mean is less than 0.02?
Answers
The probability that the difference between the sample mean and the population mean is less than 0.02 can be calculated using the standard error of the mean.
Given:
Population mean (μ) = $3.20
Population standard deviation (σ) = $0.20
Sample size (n) = 16
First, we need to calculate the standard error of the mean (SEM), which is the standard deviation of the sample mean:
\(SEM = \sigma / \sqrt n\)
Substituting the values:
SEM = \(0.20 / \sqrt{16\)
= 0.20 / 4
= $0.05
Next, we can calculate the z-score, which represents the number of standard deviations the sample mean is away from the population mean:
z = (sample mean - population mean) / SEM
z = 0.02 / $0.05
= 0.4
Using a standard normal distribution table, find the probability associated with the z-score of 0.4. The probability is the area under the curve to the left of the z-score.
Therefore, the probability that the difference between the sample mean and the population mean is less than 0.02 is the probability associated with the z-score of 0.4.
Learn more about z-scores and probability here:
https://brainly.com/question/32787120
#SPJ4
if a+b=c then b=
pls answr
Answers
Answer:
b = c - aStep-by-step explanation:
if a+b=c then b=
a + b = c
b = c - a
I need help with this last question I have here

Answers
Answer:
its d
Step-by-step explanation:
Answer:
C.
Step-by-step explanation:
The "quotient" is what you get after you divide 2 number, and in this case, you are dividing m/6.
The cost price of the shoes are $50. The selling price of the shoes are 300% of the cost price. What is the selling price of the shoes? *
Answers
Answer:
47 or 200
Step-by-step explanation:
Help me plzz so I don’t fail

Answers
Answer:
A
Step-by-step explanation:
(-2,5)
read the X axis and then y axis
simplify the following rational expression. be sure to state the condition.
x^2+5x+6/3x+6
Answers
The simplified rational expression of \(\frac{x^{2}+5x + 6 }{3x + 6}\) is \(\frac{x+3}{3}\).
How to simplify rational expression?The rational expression can be simplified as follows:
\(\frac{x^{2}+5x + 6 }{3x + 6}\)
Lets' factorise the numerator and the denominator individually.
x² + 5x + 6
x² + 2x + 3x + 6
x(x + 2) + 3(x + 2)
(x + 3)(x +2)
Therefore, let's factorise the denominator.
3x + 6
3(x + 2)
Therefore,
\(\frac{x^{2}+5x + 6 }{3x + 6} = \frac{(x+2)(x+3)}{3(x+2)} = \frac{x+3}{3}\)
Hence, the simplified expression of \(\frac{x^{2}+5x + 6 }{3x + 6}\) is \(\frac{x+3}{3}\)
learn more on rational expression here: https://brainly.com/question/1928496
#SPJ1
Adventure Time
Come on grab your friends
We'll go to very distant lands
With Jake the Dog and Finn the Human
The fun will never end, it's Adventure Time!
Answers
Answer:
so i graphed it and it does end
Step-by-step explanation:
Answer:
Adventure time is a great show they shouldve made more episodes
Step-by-step explanation:
show that 3x4 1 is o(x4∕2) and x4∕2 is o(3x4 1).
Answers
3\(x^4\) + 1 is equivalent to \(x^{(4/2)}\) in terms of asymptotic growth rate. The value of 3\(x^4\) + 1 is O(\(x^{(4/2)}\)) and \(x^{(4/2)}\) is O(3\(x^4\) + 1).
To show that 3\(x^4\) + 1 is O(\(x^{(4/2)}\)), we need to find a constant C and a value of x such that:
|3\(x^4\) + 1| <= C|\(x^{(4/2)}\)|
For x >= 1, we can say that:
3\(x^4\) + 1 <= 4\(x^4\)
Taking the square root of both sides, we get:
sqrt(3\(x^4\) + 1) <= 2x²
Thus, we can choose C = 2 and x0 = 1, and we have:
|3\(x^4\) + 1| <= 2|\(x^{(4/2)}\)| for all x >= 1
Therefore, 3\(x^4\) + 1 is O(\(x^{(4/2)}\)).
To show that \(x^{(4/2)}\) is O(3\(x^4\) + 1), we need to find a constant C and a value of x such that:
|\(x^{(4/2)}\)| <= C|3\(x^4\) + 1|
For x >= 1, we can say that:
\(x^{(4/2)}\) <= x²
Thus, we can choose C = 1 and x0 = 1, and we have:
|\(x^{(4/2)}\)| <= |3\(x^4\) + 1| for all x >= 1
Therefore, \(x^{(4/2)}\) is O(3\(x^4\) + 1).
Since both 3\(x^4\) + 1 is O(\(x^{(4/2)}\)) and \(x^{(4/2)}\) is O(3\(x^4\) + 1).
Learn more about asymptotic growth at
https://brainly.com/question/28918543
#SPJ4
Su Li wants to place a protective covering over a rectangular flower bed that measures 3.2 meters by 4.3 meters. How many square meters of covering will she need
Answers
The formula A = l w is used to calculate the area of a rectangle, which is 13.76 square meters. Su Li needs 13.76 square meters of covering for the rectangular flower bed.
The formula to calculate the area of a rectangle is given by:A = l × w Where, A = Area of rectangle l = length of rectangle w = width of rectangle Given that the rectangular flower bed measures 3.2 meters by 4.3 meters. So,Length of rectangular flower bed, l = 3.2 meters Width of rectangular flower bed, w = 4.3 meters Using the above formula, we can find the area of the rectangular flower bed. A = l × w= 3.2 meters × 4.3 meters= 13.76 square meters Therefore, Su Li will need 13.76 square meters of covering for the rectangular flower bed. Hence, the answer is 13.76 square meters of covering.
To know more about area of a rectangle Visit:
https://brainly.com/question/12019874
#SPJ11
If I roll 2 dice, what is the
probability that their total is a
prime number?
Answers
Answer:
The logic is there are six sides to each die, so for each number on one die you can pair with six different numbers on the other die. Therefore, the probability of rolling a prime number on two dice is 15/36, which reduces to 5/12
In exercises 43 through 46, solve the given separable initial value problem.
43. Dy/dx = -2y; y = 3 when x = 0
44. Dy/dx = xy; y = 1 when x = 0
45. Dy/dx = e^(x+y); y = 0 when x = 0 46, dy/dx = √(y/x') y = 1 when x =1
Answers
The initial value of the given problems are \(y = 3e^{(-2x)}, y = e^{(x^{2/2)}}, y(x) = ln|e^x - 1| and y(x) = (2/3)(x^{(3/2)} + 7)^{2/3}.\)
The given differential equation is dy/dx = -2y; y = 3 when x = 0.
Here,
dy/dx = -2y
dy/y = -2dx
Integrating both sides
ln|y| = -2x + C
here C is the constant of integration.
Now to solve for C, the initial condition y = 3 when x = 0:
ln|3| = -2(0) + C
C = ln|3|
Then, the solution to the differential equation
ln|y| = -2x + ln|3|
ln|y/3| = -2x
\(y/3 = e^{(-2x)}\)
\(y = 3e^{(-2x)}\)
The given differential equation is dy/dx = xy; y = 1 when x = 0.
Similarly the other questions can be done by the same method,
dy/y = x dx
Integrating both sides
\(ln|y| = (x^2)/2 + C\)
here C is the constant of integration.
To solve for C, the initial condition y = 1 when x = 0:
\(ln|1| = (0^2)/2 + C\)
C = 0
The n, the solution to the differential equation
\(ln|y| = (x^2)/2\)
\(|y| = e^(x^2/2)\)
\(y = ±e^{(x^2/2)}\)
Since y(0) = 1, we have:
\(y = e^{(x^{2/2})}\)
For the next question
\(dy/dx = e^{(x+y)}\); y = 0 when x = 0
\(dy/e^{y} = e^x dx\)
Integrating both sides
\(ln|e^y| + C_1= e^x + C_2\)
here C_1 and C_2 are constants of integration.
\(y(x) = ln|C_3e^x - 1|\)
Here C_3 is a constant of integration.
Utilizing the initial condition y(0) = 0:
\(y(x) = ln|e^x - 1|\)
Now,
\(dy/dx = \sqrt{(y/x')};\) y(1) = 1
\(sqrt{(y)} dy= sqrt{(x')} dxdxdxdx\)
Integrating both sides gives:
\((2/3)y^{(3/2)} + C_4= (2/3)x^{(3/2)} + C_5\)
here C_4 and C_5 are constants of integration.
\(y(x) = (2/3)(x^{(3/2)} + C_6)^{2/3}\)
here C_6 is a constant of integration.
Utilizing the initial condition y(1) = 1
\(y(x) = (2/3)(x^{(3/2)} + 7)^{2/3}\)
To learn more about differential equation
https://brainly.com/question/28099315
#SPJ4
can you make sure i'll understand

Answers
Answer:
232 lifeboats are needed for a cruise ship containing 2,315 people.
Step-by-step explanation:
A small ship can hold 463 people.
A cargo ship can hold 8,583 people
A cruise ship can hold unknown people
A battle ship can hold 17,402 people
To find the unknown:
If a cruise ship can hold 5 times the amount of people on a small ship. You must do 463 × 5 = 2,315. Therefore, a cruise ship can hold 2,315 people.
To find out how many lifeboats a cruise ship needs:
Put the numbers into a ratio. If there needs to be 1 lifeboat for every 10 passengers the ratio is 1 : 10. Substitute the values into a ratio, for every 2,315 passengers there must be unknown lifeboats.
1 : 10
? : 2,315
Must do 2,315 ÷ 10 = 232 (rounded answer) [231.5]
(YOU MUST ROUND THE ANSWER UP TO GET A WHOLE NUMBER BECAUSE IN THESE TYPES OF QUESTION YOU CANNOT HAVE A DECIMAL)
So 232 lifeboats are needed for a cruise ship containing 2,315 people.
find the critical value za/2 that corresponds to a 80 confidence level
Answers
the critical value zα/2 that corresponds to an 80% confidence level is approximately 1.2816.
To find the critical value zα/2 that corresponds to an 80% confidence level, we need to determine the value of α/2.
A confidence level of 80% implies that the remaining area under the standard normal distribution curve is (1 - 0.80) = 0.20.
Since the standard normal distribution is symmetric, we divide this remaining area equally between the two tails, resulting in
α/2 = 0.10.
To find the corresponding critical value, we look up the z-score that corresponds to an area of 0.10 in the standard normal distribution table (also known as the z-table) or use a statistical calculator.
The critical value zα/2 for α/2 = 0.10 is approximately 1.2816.
Therefore, the critical value zα/2 that corresponds to an 80% confidence level is approximately 1.2816.
Learn more about confidence level here
https://brainly.com/question/10018690
#SPJ4