Find the derivative of the given expression. y = In (√20x^3 – 13x^2 (11x^3 + 11x^2))
Answers
The derivative of y with respect to x is: dy/dx = (3 - 2860x^2 - 2288x)/(2(√20x^3 – 143x^5 – 143x^4))
To find the derivative of y = ln(√20x^3 – 13x^2(11x^3 + 11x^2)), we will need to use the chain rule and the product rule.
First, let's simplify the expression inside the natural logarithm:
√20x^3 – 13x^2(11x^3 + 11x^2) = √20x^3 – 143x^5 – 143x^4
Now we can apply the chain rule:
y = ln(√20x^3 – 143x^5 – 143x^4)
dy/dx = 1/(√20x^3 – 143x^5 – 143x^4) × d/dx(√20x^3 – 143x^5 – 143x^4)
Next, we will use the product rule to differentiate the expression inside the parentheses:
d/dx(√20x^3 – 143x^5 – 143x^4) = d/dx(√20x^3) – d/dx(143x^5) – d/dx(143x^4)
Using the power rule and the chain rule, we can simplify this to:
d/dx(√20x^3) - 715x^4 - 572x^3
Now we can substitute this back into the chain rule:
dy/dx = 1/(√20x^3 – 143x^5 – 143x^4) × (3/2√5x^2 - 715x^4 - 572x^3)
Therefore, the derivative of y with respect to x is:
dy/dx = (3 - 2860x^2 - 2288x)/(2(√20x^3 – 143x^5 – 143x^4))
To know more about power rule visit:
https://brainly.com/question/30226066
#SPJ11
Related Questions
Double tap to add title • AC is the diameter of the circle. Angle AWB is 120 degrees. How big is arc BC? A 1200 B w C D 45 Notes Comm

Answers
Answer: 60
Step-by-step explanation:

What is 4.127 × 10 to the 9th power in standard form?
A 4,127,000
B 41,270,000
C 412,700,000
D 4,127,000,000
Answers
The standard form of the given scientific notation is 4,127,000,000. Therefore, the correct answer is option D.
The given number is 4.127×10⁹.
Scientific notation is a method for expressing a given quantity as a number having significant digits necessary for a specified degree of accuracy, multiplied by 10 to the appropriate power such as 1.56×10⁷.
Here,
4.127×10⁹ = 4.127×1000000000
= 4,127,000,000
Therefore, the correct answer is option D.
To learn more about the Scientific notation visit:
https://brainly.com/question/18073768.
#SPJ6
Find the general solution of the differential equation
\( \frac{dy}{dx} = \frac{ {1 + y}^{2} }{ {1 + x}^{2} } \)
Answers
\({ \blue{ \tt{ { \tan }^{ - 1} y - { \tan}^{ - 1} x = c}}}\)
Step-by-step explanation:
This can be written as,
\({ \red{ \tt{ \frac{dy}{ {1 + y}^{2} } = \frac{dx}{1 + {x}^{2} }}}}\)
Integrate on both sides
\({ \red{ \tt{∫ \frac{ 1}{1 + {y}^{2}}}}}{ \red{ \tt{dy}}} \: = { \red{ \tt{∫ \frac{1}{1 + {x}^{2} }}}}{ \red{ \tt{dx}}} \)
\({ \red{ \tt{ { \tan}^{ - 1} y = { \tan }^{ - 1} x + c}}}\)
\({ \red{ \tt{ { \tan }^{ - 1}y - { \tan }^{ - 1}x = c}}}\)
HEJEKEKFLSKSLCBDMLDgbnnbvgfknfnfkskskfjgjdkwkdjdkdkdkdjdks
Answers
Answer:
um.... 17??????????????????
Answer:
HDHEHFGEWGDYDGYDHWQFSWDWSQWYUWEHWW8WDWD
Step-by-step explanation:BHDHEJKNHRGHRFYRHDHNHNEBFDYHFBVUUUFHECHFHVYGDFRFHRHFFRUFYYRFFRYFYFYRFREYRYFGFWYBGT
A. Name a line segment
B. Name an endpoint

Answers
Answer:
Line Segment = FG
Endpoint = C
Step-by-step explanation:
Line segment means a piece of the line
Endpoint meant a point on the end
Answer:
Step-by-step explanation:
AB is a line segment
An end point would be point C on CD
Find a unit rate: Joel ran 1500 meters in 6 minutes, 15 seconds.
Answers
Answer:
240 metres per minute
Step-by-step explanation:
1500 / 6.25 = 240
to solve a percentage problem, you have three possible questions: what is the total amount if you know the percentage rate and the part of the total amount? what is the percentage rate if you know the total amount and the part of the total amount? what is the part of the total if you know the percentage rate and the total? for number one, what must you do to get the total amount?
Answers
To determine the total amount in a percentage problem when given the percentage rate and the part of the total amount, you need to divide the part by the percentage rate and multiply the result by 100.
To find the total amount when you know the percentage rate and the part of the total amount, you can use the following formula:
Total Amount = (Part of Total Amount) / (Percentage Rate)
Let's break it down step by step:
1.Identify the given values:
Part of Total Amount: This represents the portion or fraction of the total amount that you know. Let's say it's denoted by P.
Percentage Rate: This is the rate or proportion expressed as a percentage. For example, if the rate is 20%, it would be written as 0.20 or 20/100.
2.Plug the values into the formula:
Total Amount = P / (Percentage Rate)
3.Calculate the total amount:
Simply divide the given part of the total amount by the percentage rate to find the total amount.
For example, let's say you know that the part of the total amount is $500 and the percentage rate is 25%. You can calculate the total amount as follows:
Total Amount = $500 / 0.25 = $2000
Therefore, the total amount would be $2000 in this case.
Learn more about percentage here:
https://brainly.com/question/31733229
#SPJ11
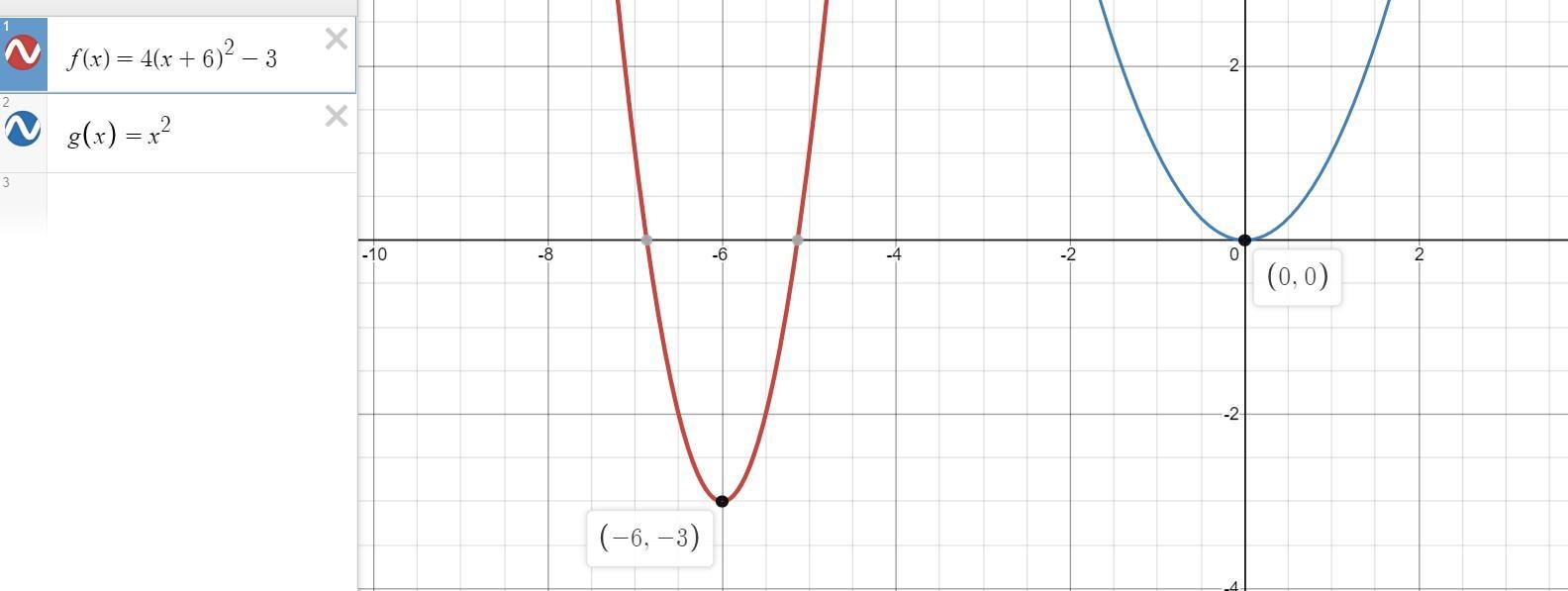
f(x) = 4(x+6)2-3
parabola; vertical stretch:4, horizontal translation right 3, vertical translation down 6.
3
parabola; vertical stretch:4, horizontal translation left 3, vertical translation up 6.
parabola; vertical stretch:4, horizontal translation left 6, vertical translation down 3.
4
parabola; vertical stretch:4, horizontal translation right 6, vertical translation down 3.
Answers
Answer:
C. parabola; vertical stretch:4, horizontal translation left 6, vertical translation down 3.Step-by-step explanation:
Given parabola:
f(x) = 4(x + 6)² - 3Its transformations from the parent function g(x) = x² are:
f(x) = 4*g(x + 6) - 34 - is a vertical stretch, 6 - is a horizontal shift left, - 3 - is a vertical shift downCorrect choice is C
What is the difference?
52 – 13 =
29
39
41
65
Answers
Answer:
39
Step-by-step explanation:
TYagVvHhisjssbahuauaahaah
How do I solve this: h + 6/5 = 2
Answers
h = 4/5
hope it helps :)
mark brainliest!
Please show your work too - thanks!

Answers
Hey there :)
Please check the attached image for answer with explanation.
\(Benjemin360 :)\)

Integrate by parts to find some useful recurrences relating Iₙ and Jₙ.
\(\displaystyle I_n = \int_{-\pi}^\pi x^n \cos(x) \, dx = uv \bigg|_{x=-\pi}^{x=\pi} - \int_{-\pi}^\pi v\, du \\\\ \implies I_n = -n \int_{-\pi}^\pi x^{n-1} \sin(x) \, dx \\\\ \implies I_n = -n J_{n-1}\)
where u = xⁿ and dv = cos(x) dx.
\(\displaystyle J_n = \int_{-\pi}^\pi x^n \sin(x) \, dx = uv \bigg|_{x=-\pi}^{x=\pi} + \int_{-\pi}^\pi v\, du \\\\ \implies J_n = \pi^n - (-\pi)^n + n \int_{-\pi}^\pi x^{n-1} \cos(x) \, dx \\\\ \implies J_n = \pi^n - (-\pi)^n + n I_{n-1}\)
The integrals for n = 0 are trivial:
\(\displaystyle I_0 = \int_{-\pi}^\pi \cos(x) \, dx = \sin(\pi) - \sin(-\pi) = 0\)
\(\displaystyle J_0 = \int_{-\pi}^\pi \sin(x) \, dx = -\cos(\pi) - (-\cos(-\pi)) = 0\)
Now, the integral we're interested in is
\(\displaystyle \int_{-\pi}^\pi x^n f(x) \cos(x) \, dx\)
but we know f(x) is quadratic, and we want to find its coefficients a, b, and c such that
\(\displaystyle \int_{-\pi}^\pi x^n (ax^2+bx+c) \cos(x) \, dx\)
But this is simply
\(\displaystyle \int_{-\pi}^\pi (ax^{n+2}+bx^{n+1}+cx^n) \cos(x) \, dx = aI_{n+2} + bI_{n+1} + cI_n\)
Using the recurrences above and the initial values we've computed, we find
• I₁ = -J₀ = 0
• J₁ = π - (-π) + I₀ = 2π
• I₂ = -2 J₁ = -4π
• J₂ = π² - (-π)² + 2 I₁ = 0
• I₃ = -3 J₂ = 0
• J₃ = π³ - (-π)³ + 3 I₂ = 2π³ - 12π
• I₄ = -4 J₃ = -8π³ + 48π
When n = 0, the integral we care about is
\(aI_2 + bI_1 + cI_0 = -4\pi a + 0 + 0 = 4\pi \implies a = -1\)
When n = 1,
\(aI_3 + bI_2 + cI_1 = 0 - 4\pi b + 0 = 4\pi \implies b = -1\)
When n = 2,
\(aI_4 + bI_3 + cI_2 = (48\pi - 8\pi^3)a + 0 - 4\pi c = 4\pi \implies c = 2\pi^2 - 13\)
so that
\(f(x) = \boxed{-x^2 - x + 2\pi^2 - 13}\)
Derivations (20 marks): For each of the questions in this section provide a derivation. Other methods will receive no credit i. ∃x(Fx & Gx) ⊢ ∃xFx & ∃xGx (5 marks)
ii. ¬ 3x(Px v Qx) ⊢ Vx ¬ Px (5 marks) iii. ¬ Vx(Fx → Gx) v 3xFx (10 marks; Hint: To derive this theorem use RA.)
Answers
¬ Vx(Fx → Gx) v 3xFx ⊢ Fx → Gx [1-5, Modus Ponens]
i. ∃x(Fx & Gx) ⊢ ∃xFx & ∃xGx (5 marks)
Proof:
1. ∃x(Fx & Gx) [Premise]
2. Fx & Gx [∃-Elimination, 1]
3. ∃xFx [∃-Introduction, 2]
4. ∃xGx [∃-Introduction, 2]
5. ∃xFx & ∃xGx [Conjunction Introduction, 3 and 4]
6. ∃x(Fx & Gx) ⊢ ∃xFx & ∃xGx [1-5, Modus Ponens]
ii. ¬ 3x(Px v Qx) ⊢ Vx ¬ Px (5 marks)
Proof:
1. ¬ 3x(Px v Qx) [Premise]
2. ¬ Px v ¬ Qx [DeMorgan’s Law, 1]
3. Vx ¬ Px [∀-Introduction, 2]
4. ¬ 3x(Px v Qx) ⊢ Vx ¬ Px [1-3, Modus Ponens]
iii. ¬ Vx(Fx → Gx) v 3xFx (10 marks; Hint: To derive this theorem use RA.)
Proof:
1. ¬ Vx(Fx → Gx) v 3xFx [Premise]
2. (¬ Vx(Fx → Gx) v 3xFx) → (¬ Vx(Fx → Gx) v Fx) [Implication Introduction]
3. ¬ Vx(Fx → Gx) v Fx [Resolution, 1, 2]
4. (¬ Vx(Fx → Gx) v Fx) → (Fx → Gx) [Implication Introduction]
5. Fx → Gx [Resolution, 3, 4]
6. ¬ Vx(Fx → Gx) v 3xFx ⊢ Fx → Gx [1-5, Modus Ponens]
Learn more about Derivations
brainly.com/question/30365299
#SPJ11
Help please,
Drag the tiles to correct boxes to complete the pair

Answers
Based on the accuracy of the test and the probability of Kevin having the disease, the following are true:
Probability that Kevin has diabetes and the test predicts this = 0.6375.Probability that Kevin has diabetes and the test doesn't predicts this = 0.1125.Probability that Kevin doesn't have diabetes and the test predicts this = 0.2125.Probability that Kevin doesn't have diabetes and the test doesn't predicts this = 0.0375.Probability that Kevin has diabetes and the test predicts this= Probability that Kevin has diabetes x Accuracy of test
= 0.75 x 0.85
= 0.6375
Probability that Kevin has diabetes and the test doesn't predicts this= Probability that Kevin has diabetes x (1 - Accuracy of test )
= 0.75 x ( 1 - 0.85)
= 0.1125
Probability that Kevin doesn't have diabetes and the test predicts this= Probability that Kevin doesn't have diabetes x Accuracy of test
= ( 1 - 0.75) x 0.85
= 0.2125
Probability that Kevin doesn't have diabetes and the test doesn't predicts this= Probability that Kevin doesn't have diabetes x (1 - Accuracy of test )
= ( 1 - 0.75) x (1 - 0.85)
= 0.0375
In conclusion, the probability depends on the accuracy of the test and the probability of having diabetes.
Find out more on probability at https://brainly.com/question/6354635.
Use the simplex algorithm to find the optimal solution to the following LP (solve manually): maxz= 36x1+30x2−3x3−4x4
s.t. x1+x2−x3≤5
6x1+5x2−x4≤10
∀xi≥0
Answers
The maximum value of z is 0, and the values of the decision variables are x1 = 0, x2 = 10, x3 = 0, x4 = 0.
maximize: z = c1x1 + c2x2 + ... + cnxn
subject to
a11x1 + a12x2 + ... + a1nxn ≤ b1
a21x1 + a22x2 + ... + a2nxn ≤ b2
am1x1 + am2x2 + ... + amnxn ≤ bmxi ≥ 0 for all i
In our case,
the given LP is:maximize: z = 36x1 + 30x2 - 3x3 - 4x
subject to:
x1 + x2 - x3 ≤ 5
6x1 + 5x2 - x4 ≤ 10
xi ≥ 0 for all i
We can rewrite the constraints as follows:
x1 + x2 - x3 + x5 = 5 (adding slack variable x5)
6x1 + 5x2 - x4 + x6 = 10 (adding slack variable x6)
Now, we introduce the non-negative variables x7, x8, x9, and x10 for the four decision variables:
x1 = x7
x2 = x8
x3 = x9
x4 = x10
The objective function becomes:
z = 36x7 + 30x8 - 3x9 - 4x10
Now we have the problem in standard form as:
maximize: z = 36x7 + 30x8 - 3x9 - 4x10
subject to:
x7 + x8 - x9 + x5 = 5
6x7 + 5x8 - x10 + x6 = 10
xi ≥ 0 for all i
To apply the simplex algorithm, we initialize the simplex tableau as follows:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0 | 36 | 30 | -3 | -4 | 0 |
---------------------------------------------------------------------------
x5| 0 | 1 | 0 | 1 | 1 | -1 | 0 | 5 |
---------------------------------------------------------------------------
x6| 0 | 0 | 1 | 6 | 5 | 0 | -1 | 10 |
---------------------------------------------------------------------------
Now, we can proceed with the simplex algorithm to find the optimal solution. I'll perform the iterations step by step:
Iteration 1:
1. Choose the most negative coefficient in the 'z' row, which is -4.
2. Choose the pivot column as 'x10' (corresponding to the most negative coefficient).
3. Calculate the ratios (RHS / pivot column coefficient) to find the pivot row. We select the row with the smallest non-negative ratio.
Ratios: 5/0 = undefined, 10/(-4) = -2.5
4. Pivot at the intersection of the pivot row and column. Divide the pivot row by the pivot element to make the pivot element 1.
5. Perform row operations to
make all other elements in the pivot column zero.
After performing these steps, we get the updated simplex tableau:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0.4 | 36 | 30 | -3 | 0 | 12 |
---------------------------------------------------------------------------
x5| 0 | 1 | -0.2 | 1 | 1 | -1 | 0 | 5 |
---------------------------------------------------------------------------
x10| 0 | 0 | 0.2 | 1.2 | 1 | 0 | 1 | 2.5 |
---------------------------------------------------------------------------
Iteration 2:
1. Choose the most negative coefficient in the 'z' row, which is -3.
2. Choose the pivot column as 'x9' (corresponding to the most negative coefficient).
3. Calculate the ratios (RHS / pivot column coefficient) to find the pivot row. We select the row with the smallest non-negative ratio.
Ratios: 12/(-3) = -4, 5/(-0.2) = -25, 2.5/0.2 = 12.5
4. Pivot at the intersection of the pivot row and column. Divide the pivot row by the pivot element to make the pivot element 1.
5. Perform row operations to make all other elements in the pivot column zero.
After performing these steps, we get the updated simplex tableau:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0.8 | 34 | 30 | 0 | 4 | 0 |
---------------------------------------------------------------------------
x5| 0 | 1 | -0.4 | 0.6 | 1 | 5 | -2 | 10 |
---------------------------------------------------------------------------
x9| 0 | 0 | 1 | 6 | 5 | 0 | -5 | 12.5 |
---------------------------------------------------------------------------
Iteration 3:
No negative coefficients in the 'z' row, so the optimal solution has been reached.The optimal solution is:
z = 0
x1 = x7 = 0
x2 = x8 = 10
x3 = x9 = 0
x4 = x10 = 0
x5 = 10
x6 = 0
Therefore, the maximum value of z is 0, and the values of the decision variables are x1 = 0, x2 = 10, x3 = 0, x4 = 0.
Learn more about Simplex Algorithm here:
https://brainly.in/question/46895640
#SPJ11
The law of large numbers states that as the number of observations drawn at random from a population with finite mean μ increases, the mean of the observed values.
Answers
The mean of a observed values approaches the population mean more and more as the number of data points gathered rises.
Define the term population mean?The average calculated from the group members, distribution, or population is known as the population mean.
It is calculated by dividing the sum of all different variables through the total population of variables. The population mean is shown here as. The population's observations are added together to form X. There are 2 distinct averages in statistics: Only a few observations—selected from the population data—are taken into account for calculating the sample mean. On the other hand, the population mean computes the average value by taking into account all of the population's observations.Thus, choose a population with a finite mean and a random sample of observations. The mean of a observed values approaches the population mean to a greater extent as the number of data gathered rises.
To know more about the population mean, here
https://brainly.com/question/15020296
#SPJ4
lodine-131 has a half-life of 8 days. How much of the original 40-gram sample would be left
after 40 days?
Answers
Answer:
1.25 grams would be left
Step-by-step explanation:
40/2=20
20/2=10
10/2=5
5/2=2.5
2.5/2=1.25
The width of a rectangle is 4 feet more than the length. If the length is doubled and the width is decreased by 2 feet, a new rectangle is formed whose perimeter is 68 feet. Find the dimensions of the original rectangle.
Answers
Answer:
Step-by-step explanation:
We'll work through this by setting up a table, as follows:
original new
width
length
It tells us the width of a rectangle is 4 feet more than the length. If we don't know the length, we'll call it L; that means that the width is L + 4, because the width is the length plus 4 more feet. Put that into column 1:
original new
width L + 4
length L
The next sentence tells us how the original rectangle is being manipulated to create a new rectangle, so that information goes into the column named "new". The original length is doubled:
original new
width L + 4
length L 2L
and the original width is decreased by 2:
original new
width L + 4 L + 4 - 2 (which simplifies to L + 2)
length L 2L
The perimeter of the new rectangle is 68. The formula for the perimeter is
P = 2L + 2w, so filling in our info along with the given perimeter:
68 = 2(L + 2) + 2(2L) and
68 = 2L + 4 + 4L and
68 = 6L + 4 and
64 = 6L so
L = \(\frac{32}{3}\) and the width then is
w = \(\frac{32}{3}+4\) so
w = \(\frac{44}{3}\)
h(a)=2a+4
g(a)-2a^2+2
find (h+g)(a+3)
Answers
Answer:
hello :
(g/f)(3) = g(3)/f(3)
but : g(3) =3(3)+2 = 11
f(3) 2(3)-4 = 2
g/f)(3) = 11/2
helpppppppppppp meeeeeeeeeeee pleaseee!!!

Answers
The y-intercept of the given graph is at (0, 1), hence g(0) = 1.
Solution to a graphThe given graph is a graph of a modulus expression. The parent form of a modulus function is given as g(x) = |x|.
The point where x = 0 is the point where the line intersect the y-axis of the graph. From the graph shown, you can see that the line intersects at only one point.
Since the y-intercept of the line is at (0, 1), hence the value of the function g(0) is equivalent to 1.
Learn more on y-intercepts here: https://brainly.com/question/24363347
#SPJ1
From a hot air balloon 2,500ft above the ground you see a clearing whose angle of depression is at 25 degrees. What is the horizontal distance form the clearing to the nearest feet
Answers
9514 1404 393
Answer:
5361 feet
Step-by-step explanation:
The tangent of the angle is the ratio of vertical distance to horizontal.
tan(25°) = (vertical distance)/(horizontal distance)
horizontal distance = (2500 ft)/tan(25°) ≈ 5361 feet
Leo wanted to surprise his brother on New Years Eve, by filling his Lightsaber full of confetti for their big dual. He needs to know how many bags to buy.


Answers
Given:
The lightsaber is filled with full of confetti.
The lightsaber:
\(\begin{gathered} h=30in \\ d=2.5in \end{gathered}\)The confetti bag is 10oz.
To find:
The number of bags of confetti.
Explanation:
The radius of the lightsaber is,
\(r=\frac{d}{2}=\frac{2.5}{2}=1.25in\)The volume of the lightsaber is,
\(\begin{gathered} V=\pi r^2h \\ =\frac{22}{7}\times1.25^2\times30 \\ V=147.32in^3 \end{gathered}\)In oz,
\(\begin{gathered} V=\frac{147.32}{1.804} \\ V=81.66oz \end{gathered}\)So, the number of bags will be,
\(\begin{gathered} n=\frac{Volume\text{ }of\text{ }lightsaber}{Volume\text{ of a bag}} \\ =\frac{81.66}{10} \\ =8.166 \\ \approx8bags \end{gathered}\)The number of bags required is 8.
Final answer:
The volume of the lightsaber is 81.66 ounces.
The number of bags required is 8.
All mortgages must be paid monthly.
A. True
B.False
Answers
Answer:
A
Step-by-step explanation:
Number 8 please I don’t know anything

Answers
Answer:
A. Domain: 1,2 Range: 0,1,4
B. Domain: 0,2,4, Range: 1,2,3,
Step-by-step explanation:
Domain is the x axis
Range is the y axis
a backyard garden has an area of 6.59 square meters. how many square centimeters is this? express your answer in scientific notation and to three significant figures.
Answers
There are 65900 square centimetres present in a backyard garden that has an area of 6.59 square meters.
Scientific notation is the way through which a very small or a very large number can be written in shorthand. In scientific notations when a number is between 1 and 10s, it is multiplied by a power of 10.
For example, 6,500,000,000,000 can be written as 6.5 × 10¹².
To calculate a square meter value to the related value in cm², just multiply the quantity in m² by 10000 (the conversion factor). Here is the formula for it:
Value in cm² = value in m² × 10000
We need to convert 6.59 m² into cm². Using the conversion formula above, we will get:
Value in cm² = 6.59 × 10000 = 65900 cm²
To know more about
https://brainly.com/question/9194021
#SPJ4
-9 (c + 7) = -13c +7
What value of c makes the equation true? Enter the answer in the box.
Answers
Answer:
c=17,5Step-by-step explanation:
-9(c+7) = -13c+7
<=> -9c - 63 = -13c+7
<=> -9c + 13c = 7+63
<=> 4c = 70
<=> c = 70/4 = 35/2 = 17,5
CHECK THE ANSWER:-9(c+7) = -13c+7
-9(17,5+7) = -13×17,5+7
-220,5 = -220,5
Hope it's help u:))If the characteristic polynomial of a 2Ã2 matrix is λ^2 â 5λ + 6, what is the determinant of the matrix?
Answers
The determinant of the matrix cannot be uniquely determined from the information given.
The characteristic polynomial of a 2x2 matrix A is given by:
p(λ) = det(A - λI) = λ^2 - tr(A)λ + det(A)
where tr(A) is the trace of A and det(A) is the determinant of A.
In this case, the characteristic polynomial of the matrix is given by:
p(λ) = λ^2 - 5λ + 6
Comparing this to the general form of the characteristic polynomial, we can see that:
- tr(A) = 5
- det(A) = 6
Since the determinant of a 2x2 matrix A is given by:
det(A) = a11*a22 - a12*a21
where aij denotes the entry in the ith row and jth column of A, we can use the fact that det(A) = 6 to solve for the determinant of the matrix. Specifically, we have:
det(A) = a11*a22 - a12*a21 = 6
We don't have enough information to determine the specific values of a11, a12, a21, and a22. However, we do know that their product is 6. For example, we could have:
a11 = 2, a12 = 3, a21 = 1, a22 = 4
which gives det(A) = 2*4 - 3*1 = 5.
Alternatively, we could have:
a11 = 6, a12 = 0, a21 = -1, a22 = -1
which also gives det(A) = 6.
Therefore, the determinant of the matrix cannot be uniquely determined from the information given.
Visit to know more about Matrix:-
brainly.com/question/2456804
#SPJ11
. How many days will it take for $9500 to earn $800 at 8.25% p.a.?
Answers
It will take approximately 39.532 days for $9500 to earn $800 at an annual interest rate of 8.25%.
To find the number of days it will take for $9500 to earn $800 at an annual interest rate of 8.25%, we need to use the formula for simple interest:
Interest = Principal * Rate * Time
In this case, we are given the interest ($800), the principal ($9500), and the annual interest rate (8.25%). We need to solve for time.
Let's denote the time in years as "t". Since we're looking for the number of days, we'll convert the time to a fraction of a year by dividing by 365 (assuming a standard 365-day year).
$800 = $9500 * 0.0825 * (t / 365)
Simplifying the equation:
800 = 9500 * 0.0825 * (t / 365)
Divide both sides by (9500 * 0.0825):
800 / (9500 * 0.0825) = t / 365
Simplify the left side:
800 / (9500 * 0.0825) ≈ 0.1083
Now, solve for t by multiplying both sides by 365:
0.1083 * 365 ≈ t
t ≈ 39.532
Therefore, it will take approximately 39.532 days for $9500 to earn $800 at an annual interest rate of 8.25%.
for such more question on annual interest rate
https://brainly.com/question/29451175
#SPJ8
min 8x₁ + 6x₂ subject to
a. 4x₁ + 2x₂ ≥ 20
b. −6x₁ + 4x₂ ≤ 12
c. x₁ + x₂ ≥ 6
d. x₁ + x₂ ≥ 0
Answers
The minimum value of the objective function subject to the given constraints is 48 and it occurs at (6,0).
The given problem is:
min 8x₁ + 6x₂ subject to4x₁ + 2x₂ ≥ 20−6x₁ + 4x₂ ≤ 12x₁ + x₂ ≥ 6x₁ + x₂ ≥ 0
The feasible region is as follows:
Firstly, plot the following lines:4x₁ + 2x₂ = 20-6x₁ + 4x₂ = 12x₁ + x₂ = 6x₁ + x₂ = 0On plotting, the following graph is obtained:
Now, let's check each option one by one:
a. 4x₁ + 2x₂ ≥ 20
The feasible region is the region above the line 4x₁ + 2x₂ = 20.
b. −6x₁ + 4x₂ ≤ 12
The feasible region is the region below the line −6x₁ + 4x₂ = 12.c. x₁ + x₂ ≥ 6
The feasible region is the region above the line x₁ + x₂ = 6.d. x₁ + x₂ ≥ 0
The feasible region is the region above the x-axis.
Now, check the point of intersection of the lines.
They are:(10,0),(2,4),(6,0)The point (2,4) is not in the feasible region as it lies outside it.
Therefore, we reject this point.
The other two points, (10,0) and (6,0) are in the feasible region.
Now, check the values of the objective function at these two points.
Objective function value at (10,0): 80
Objective function value at (6,0): 48
Therefore, the minimum value of the objective function subject to the given constraints is 48 and it occurs at (6,0).
Know more about the function here:
https://brainly.com/question/11624077
#SPJ11
Find the first four nonzero terms in a power series expansion about x0 for a general solution to the given differential equation. 0
Answers
Answer:
Start with equation,
y''(x) = f(x) = 6y/(10x-x²) about point x₀ = 5
Then,
y(x) = a₀ + a₁(x-5) + a₂(x-5)²+ a₃(x-5)³ + a₄(x-5)⁴...….
by inspection,
y(5) = a₀ and y'(5) = a₁
then,
y''(5) = 6a₀/(50-25) = 6a₀/25
y'''(x) = 6y'/(10x-x2) - 6y(10-2x)/(10x-x2)2
then,
y'''(5) = 6a₁/25 - 0 = 6a₁/25
y''''(x) = 6y''/(10x-x2) -12y'(10-2x)/(10x-x2)² + 12y/(10x-x2)² + 12y(10-2x)2/(10x-x2)³
then,
y''''(5) = (6/25)(6a₀/25) + 0 + 12a₀/625 + 0
= 48a₀/625
So,
y(x) = f(x) = f(5) + f'(5)(x-5) + f''(5)(x-5)2/2! + f'''(5)(x-5)3/3! + f''''(5)(x-5)4/4! …
or
y(x) = f(x) = a₀ + a₁(x-5) + (6ao/25)(x-5)2/2! + (6a1/25)(x-5)3/3! + (48a₀/625)(x-5)4/4!...
or
y(x) = f(x) = a₀ + a₁(x-5) + (3a₀/25)(x-5)²+ (a₁/25)(x-5)³+ (2a₀/625)(x-5)⁴.....
Learn more about equation here-
https://brainly.com/question/3391581
#SPJ4
Need help on this question asap pleasee please

Answers
Given:
A regular pentagon with side 8 cm and apothem 6 cm.
To find:
The area of the given regular pentagon.
Solution:
The area of a regular polygon is:
\(A=\dfrac{n\times s\times a}{2}\)
Where, n is the number of sides of the regular polygon, s is the side length and a is the apothem.
In a regular pentagon the number of sides is 5.
Substituting \(n=5,s=8,a=6\) in the above formula, we get
\(A=\dfrac{5\times 8\times 6}{2}\)
\(A=\dfrac{240}{2}\)
\(A=120\)
The area of the regular pentagon is 120 cm². Therefore, the correct option is C.