Find the distance between the points (6, -2) and (9,4).
Answers
Answer:
75 units
Step-by-step explanation:
Answer:
5 units
Step-by-step explanation:
answer given by IXL
Related Questions
what fraction represents 70%
Answers
Answer:
7/10
Step-by-step explanation:
Answer:
7/10
Percent to fraction conversion table
Percent Fraction
62.5% 5/8
66.67% 2/3
60% 3/5
70% 7/10
28 more rows
Step-by-step explanation:
pls help quick 10 points

Answers
Answer:
6.86 to 2DP.
Step-by-step explanation:
7/12 = 4/DC
Cross multiply:
7DC = 4*12
DC = 48/7
= 6.857.
please help with the question below (please add an explanation)

Answers
In order to get the volume of the irregular figure, let's cut it into two regular figures. See the cut below.
First, let's calculate the volume of the upper part.
The dimensions of the upper part are 7cm by 3 cm by 3 cm. Since the shape is a rectangular prism, let's multiply 7, 3, and 3.
\(V_{upper}=7cm\times3cm\times3cm=63cm^3\)Hence, the volume of the upper figure is 63 cm³.
Let's now calculate the volume of the lower figure.
The dimensions of the lower figure are 5cm by 4 cm by 3 cm. Since this is a rectangular prism too, let's multiply the dimensions.
\(V_{lower}=5cm\times4cm\times3cm=60cm^3\)The volume of the lower figure is 60 cm³.
Let's add the volume of the two figures to get the volume of the entire irregular figure.
\(V_{irregular}=V_{upper}+V_{lower}\)\(V_{irregular}=63cm^3+60cm^3=123cm^3\)Therefore, the entire volume of the given irregular figure is 123 cm³.



The sum
of two numbers is 72. The difference is
22. Find the two numbers.
Answers
Answer:
b= 25
Step-by-step explanation:
a+b =72
a-b = 22
2a = 94
DBS(Divide Both Side) by 2
a = 47
=47 +b =72
and:
47 -b =22
subtract 47 from both sides:
b=25
and
-b = -25 MBS(Multiply Both Side) by-1 ....>b=25
Kyle just graduated from college and got his first job, he has $45,000 in student loan debt, wants to buya new car, and is considering opening up a retirement account. He has a disposable income of$300/month, what would you recommend he do with this money? Why?
Answers
Problem
Kyle just graduated from college and got his first job, he has $45,000 in student loan debt, wants to buy a new car, and is considering opening up a retirement account. He has a disposable income of $300/month, what would you recommend he do with this money? Why?
Solution
For this case the best option would be put the $45000 in a bank with a compound interest
And with the earnings each month of 300$ he can put the half of this into the account and the remain to spend on other things
PLS PLS PLS PLS PLS HELP
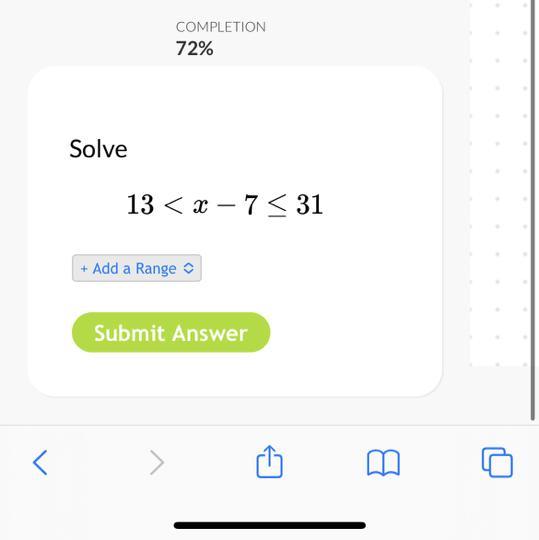
Answers
Answer: (
20
,
38
]
Step-by-step explanation:
(20,38]
Please help work this equation
Step-by-step explanation is needed.
100 points
5 stars ⭐️ ⭐️⭐️⭐️⭐️
And a thanks

Answers
Hi!
Given these two equations:
\(x = y + 8\)
\(x + 4 = 2(y + 4)\)
We want to solve using the substitution method. Knowing that x is equal to y + 8, we can simply plug in 'y + 8' in for x in the second equation, like so:
\((y+8)+4=2(y+4)\)
Combine like terms on both sides:
\(y+12=2y+8\)
Subtract y from both sides:
\(12=y+8\)
Subtract 8 from both sides:
\(y=4\)
Now, we can simply plug the y value in to the first equation, and solve for x:
\(x=4+8\)
Simplify:
\(x=12\)
Therefore, x is equal to 12 and y is equal to 4.Learn more about the substitution (and also elimination!) method here:
https://brainly.com/question/14619835
Change the word phrase to an algebraic expression. Use x to represent the number. The product of 9 and two more than a number
Answers
The algebraic expression for "The product of 9 and two more than a number" is 9(x + 2).
In the given word phrase, "a number" is represented by the variable x. The phrase "two more than a number" can be translated as x + 2 since we add 2 to the number x. The phrase "the product of 9 and two more than a number" indicates that we need to multiply 9 by the value obtained from x + 2. Therefore, the algebraic expression for this word phrase is 9(x + 2).
"A number": This is represented by the variable x, which can take any value.
"Two more than a number": This means adding 2 to the number represented by x. So, we have x + 2.
"The product of 9 and two more than a number": This indicates that we need to multiply 9 by the value obtained from step 2, which is x + 2. Therefore, the algebraic expression becomes 9(x + 2).
In summary, the phrase "The product of 9 and two more than a number" can be algebraically expressed as 9(x + 2), where x represents the number.
Learn more about algebraic expression:
https://brainly.com/question/4344214
#SPJ11
A prism has a volume of 405 cubic inches. A prism has a length of 15 inches, height of h, and width of 4.5 inches. Which is the correct substitution for finding the height of the prism? V = l w h. 405 = 15 + 4.5 + h. V = l w h = 15 times 4.5 times 405 V = l w h = 15 times 4.5 times 15 V = l w h. 405 = 15 times 4.5 times h
Answers
Answer:
d) 405 = 15 times 4.5 times h
The height of the prism 'h' = 6 inches
Step-by-step explanation:
Explanation:-
Given Volume of prism
V = 405 cubic inches
Given length of the prism
L = 15 inches
Given width of the prism
W = 4.5 inches
The volume of the prism
V = l w h
405 = 15 ×4.5× h
405 = 67.5 h
Dividing '67.5' on both sides , we get
h = 6 inches
Final answer:-
The height of the prism 'h' = 6 inches
Answer: V = l w h. 405 = 15 times 4.5 times h
Step-by-step explanation:
Given the following :
Volume of prism = 405 in^3
Length = 15 inches
Height = h
Width = 4.5 inches
Recall :
The volume of a prism is the product of the Base and the height.
That is;
Volume = Base × height
However, Base of prism is given by the area of the base shape of the prism.
From our parameters Base shape of the prism is a rectangle.
Therefore, Area of rectangle = Length × width
= 15 inches × 4.5 inches = 67.5 inch^2 = Base of prism
Therefore, Volume of prism equals ;
Volume = 15 × 4.5 × h
Volume = 405in^3
Volume = Base × height
405 = 15 × 4.5 × h
Evaluate the expression.
5+ [4•3(2 + 1)]
Answers
Answer:
41
Step-by-step explanation:
The bottom of a cup has a diameter of 5 centimeters. Which is closest to the area of
the bottom of the cup?
A
7.85 cm
B
15.71 cm
С
19.63 cm
D
78.54 cm
A
С
D
Answers
For which inequality would x = 5 be a solution?x - 4 > 8x + 7 ≥ 128 x ≤ 25.445 ÷ x < 9
Answers
Given:
Given that the four inequalities.
And the solution.
\(x=5\)Required:
To find which inequality would x = 5 be a solution.
Explanation:
(1)
\(\begin{gathered} x-4>8 \\ 5-4=1<8 \end{gathered}\)Therefore x=5 is not a solution.
(2)
\(\begin{gathered} x+7\ge12 \\ 5+7=12 \\ 12\ge12 \end{gathered}\)Therefore, x=5 is a solution.
(3)
\(\begin{gathered} 8x\leq25.4 \\ 8(5)=40 \\ 40>25.4 \end{gathered}\)Therefore, x=5 is not a solution.
(4)
\(\begin{gathered} \frac{45}{x}<9 \\ \frac{45}{5}=9 \\ 9=9 \end{gathered}\)Therefore x=5 is not a solution.
Final Answer:
x=5 is as solution for the inequality,
\(x+7\ge12\)
2 Which ordered pairs represent vertices of the
polygon?
Circle THREE correct answers.
(-11, 13)
(1, -1)
(1/4 , 2 2/1)
(1,-3)
Answers
The ordered pairs representing the vertices of a polygon are
(-11, 13) , (1, -1) and (1,-3).
Given, the ordered pairs representing the vertices of the polygon.
as, the given ordered pairs are
(-11, 13) , (1, -1) , (1/4 , 2(2/1)) , (1,-3).
Now, from the given ordered pairs
the pairs which are representing the vertices of a polygon are
(-11, 13) , (1, -1) and (1,-3).
So, the ordered pairs representing the vertices of a polygon are (-11, 13) ,
(1, -1) and (1,-3).
Hence, the ordered pairs representing the vertices of a polygon are
(-11, 13) , (1, -1) and (1,-3).
Learn more about Coordinate Geometry here https://brainly.com/question/18269861
#SPJ1
A differentiable function y(x), and x > 0, that satisfies the IVP y’ |x|, y(-1)= 2 is
Answers
To find a differentiable function y(x) that satisfies the initial value problem (IVP) y' = |x| and y(-1) = 2, we can integrate the given differential equation and then apply the initial condition.
Integrating both sides of the differential equation y' = |x| with respect to x, we get:
∫ y' dx = ∫ |x| dx
Integrating ∫ y' dx gives us y(x) + C₁, where C₁ is an arbitrary constant of integration.
Integrating ∫ |x| dx involves considering the different cases for x. Since x > 0 (as given in the problem), we have:
∫ |x| dx = ∫ x dx (for x > 0)
= (x^2)/2 + C₂, where C₂ is another arbitrary constant of integration.
Now, we have:
y(x) + C₁ = (x^2)/2 + C₂
To determine the values of C₁ and C₂, we can use the initial condition y(-1) = 2:
y(-1) + C₁ = ((-1)^2)/2 + C₂
2 + C₁ = 1/2 + C₂
Simplifying further:
C₁ = 1/2 - 2 + C₂
C₁ = C₂ - 3/2
We can rewrite the equation for y(x) by substituting C₁ with C₂ - 3/2:
y(x) = (x^2)/2 + (C₂ - 3/2)
Therefore, a differentiable function that satisfies the given IVP y' = |x| and y(-1) = 2 is:
y(x) = (x^2)/2 + (C₂ - 3/2), where C₂ is an arbitrary constant.
Learn more about differentiable function here:
https://brainly.com/question/18962394
#SPJ11
The perimeter of a rectangle of length 4 cm and width 9 cm is:
A. 26cm
B. 13cm
C. 36cm
D. 26m
Answers
Perimeter of a Rectangle
0Save
Perimeter of the rectangle = PQ + QR + RS + SP
= b +l + b + l
= 2b +2l
Again,
ABCD is a rectangle. We know that the opposite sides of a rectangle are equal.
Perimeter of a Rectangle
AB = CD = 5 cm and BC = AD = 3 cm
So, the perimeter of the rectangle ABCD = AB + BC + CD + AD = 5 cm + 3 cm + 5 cm + 3 cm = 16 cm
It can be written as 5 cm + 5 cm + 3 cm + 3 cm
= (2 × 5) cm + (2 × 3) cm
= 2 (5 + 3) cm
= 2 × 8 cm
= 16 cm
PLS HELP(Identifying Functions LC) Which of the following tables represents a relation that is a function?
x y
2 −5
2 −3
2 0
2 3
2 5
x y
−3 0
−1 3
0 4
3 0
4 3
x y
−4 2
−3 2
0 −2
0 2
4 2
x y
−4 −2
−3 4
−1 −1
−1 2
3 −3
Answers
Answer:
Option 2
x y
−3 0
−1 3
0 4
3 0
4 3
Step-by-step explanation:
For a relation x → y to be a function, there can be one and only one value of y for a value of x
Looking at the tables we see that option 1 is out since all x values are 2 andthere are multiple values of y
The last option is out because for x = 0 there are two values of y=-2 and y = 2
Correct choice is the second option which has a unique y value for each value of x
Answer:
option 2 im doing it rn
Step-by-step explanation:
HELP ASAP I WILL MARK BRAINLEST
Internet Usage The number of hours people in the United States
spent using the Internet each year from 1998 to 2001 can be
modeled by the function f(x) 5 26.4x 1 54.4 where x is the number
of years since 1998.
a. Graph the function and identify its domain and range.
b. Find the number of hours that people spent on the Internet
in 2000. Explain how you found your answer.
c. When did people spend about 120 hours per year on the
Internet? Explain how you found your answer.
Answers
Answer:
Look in picture
Step-by-step explanation:

Functions can be represented on graph and as equation.
The domain and the range of the function are [0,3] and [54.4,133.6]The number of hours spent in 2000 is 107.2People spend about 120 hours per year in 2001The function is given as:
\(f(x) = 26.4x + 54.4\)
(a) The graph, domain and range
See attachment for the graph of \(f(x) = 26.4x + 54.4\)
The function represents years from 1998 to 2001.
This means that:
\(x = 0\) in 1998 and \(x =3\) in 2001
So, the domain is: \([0, 3]\)
From the graph;
\(x = 0 \to f(x) = 54.4\)
\(x = 3 \to f(x) = 133.6\)
So, the range is \([54.4,133.6]\)
(b) Number of hours spent in 2000
First, we calculate x.
\(x = 2000 - 1998\)
\(x =2\) i.e. 2 years since 1998
So, we have:
\(f(x) = 26.4x + 54.4\)
\(f(2) =26.4 \times 2 + 54.4\)
\(f(2) =107.2\)
(c) When people starts to spend 120 hours.
We have:
\(f(x) = 26.4x + 54.4\)
Substitute 120 for f(x)
\(120 = 26.4x + 54.4\)
Collect like terms
\(26.4x = 120 - 54.4\)
\(26.4x = 65.6\)
Solve for x
\(x = \frac{65.6}{26.4}\)
\(x = 2.48\)
Round 2.48 to the smallest integer greater than 2.48
\(x = 3\)
This represents the number of years, since 1998.
So, the actual year is:
\(Year =1998 + 3\)
\(Year = 2001\)
Hence, people spend about 120 hours per year in 2001
Read more about functions and graphs at:
https://brainly.com/question/18806107

Find the circumference of the circle, round to the nearest tenth. Answer: H
Answers
Answer:
H
Step-by-step explanation:
I NEED HELP ON THIS ASAP!!!!!!!


Answers
The range of values that we are permitted to enter into our function is known as the domain of a function. The x values for a function like f make up this set (x). A function's range is the collection of values it can take as input.
What does a calculus domain mean?The collection of all potential inputs for a function is its domain. For instance, the domain of f(x)=x2 and g(x)=1/x are all real integers with the exception of x=0.
How to Determine a Function's Range?Think about the function y = f. (x). The range of the function is the range of all the y values, from least to maximum. Substitute all possible values of x into the provided expression of y to see whether it is positive, negative, or equal to other values.
To know more about function visit:-
brainly.com/question/12431044
#SPJ1
What is an equation of the line that passes through the points (8, 2) and (-4,5)? Put your answer in fully reduced form.
Answers
Answer:
y = -1/4x + 4
choose similar polygons have areas of 128 in2 and 98 in 2. if the smaller polygon has a perimeter of 42 inches what is the perimeter of the larger polygon 
Answers
Let the smaller polygon have side lengths a and the larger polygon have side lengths b. Since the polygons are similar, the ratio of corresponding side lengths is the same as the ratio of their areas. That is:
b^2 / a^2 = 128 / 98
Simplifying this expression, we get:
b / a = √(128 / 98) = √(64 / 49) = (8 / 7)
Now we can use the fact that the perimeter of the smaller polygon is 42 inches:
4a = 42
a = 10.5
Substituting this into the ratio we found above, we get:
b = (8 / 7) * a = (8 / 7) * 10.5 = 12
Therefore, the larger polygon has a perimeter of:
4b = 4 * 12 = 48 inches.
If X and Y are independent random variables with means ux= 10.5 and uy= 5.7, and standard deviations ox = 0.5 and oy= 0.3. 1) Find E[3X + 2Y] 2) Find Var[2X] 3) Find Var[X - Y] 4) Find Var[3X + 2Y].
Answers
The expected value of 3X + 2Y is 42.9. The variance of 2X is 1. The variance of X - Y is 0.34. The variance of 3X + 2Y is 2.61.
E[3X + 2Y]:
Since X and Y are independent random variables, the expected value of their linear combination can be calculated by applying the linearity of expectation.
E[3X + 2Y] = 3E[X] + 2E[Y] = 3 * 10.5 + 2 * 5.7 = 31.5 + 11.4 = 42.9
Therefore, E[3X + 2Y] is equal to 42.9.
Var[2X]:
To find the variance of a constant multiple of a random variable, we square the constant and multiply it by the variance of the random variable.
Var[2X] = (2^2) * Var[X] = 4 * (0.5^2) = 4 * 0.25 = 1
Therefore, Var[2X] is equal to 1.
Var[X - Y]:
Since X and Y are independent, the variance of their difference is the sum of their individual variances.
Var[X - Y] = Var[X] + Var[Y] = (0.5^2) + (0.3^2) = 0.25 + 0.09 = 0.34
Therefore, Var[X - Y] is equal to 0.34.
Var[3X + 2Y]:
Again, using the linearity of variance, we can calculate the variance of the linear combination of independent random variables.
Var[3X + 2Y] = (3^2) * Var[X] + (2^2) * Var[Y] = 9 * (0.5^2) + 4 * (0.3^2) = 9 * 0.25 + 4 * 0.09 = 2.25 + 0.36 = 2.61
Therefore, Var[3X + 2Y] is equal to 2.61.
To know more about variance,
https://brainly.com/question/31964048
#SPJ11
In mrs kuliks class there are 20 female students and 8 male students what is the percent of male students
Answers
Answer:
About 29%
Step-by-step explanation:
An analysis of regression measures only the variance in ____ because it is the value we want to predict.
Answers
Answer:
Y is the awnser
Step-by-step explanation:
So i have to move numbers into the right box, there is 4 boxes labelled Quadrant I, Quadrant II, Quadrant III, and Quadrant IVI have to drag the numbers (6, -1) (-3,4) (2,4) and (-1, -5) into the right Quadrant boxes, which do I drag to which box? Sorry if that was hard to understand you can just tell me I will still give you a good rating,
Answers
The signs of the coordinates in the quadrants are given as follows:
In quadrant I, the coordinates are given as (x,y).
In quadrant II, the coordinates are given by (-x,y).
In quadrant III, the coordinates are given by (-x,-y).
In quadrant IV, the coordinates are given by (x,-y).
Using the above data, drag (6,-1) to quadrant IV.
Drag (-3,4) to to quadrant II.
Drag (2,4) to quadrant I.
Drag (-1,-5) to quadrant III.
Molly purchased a car for $16,079 at 3.6% add-on rate for 4 years. Determine the amount of interest and the monthly payment for the car loan.
$3,010.16 ; $310.50
$3,010.16 ; $383.22
$2,315.38 ; 310.50
$2,315.38 ; $383.22
Answers
the correct answer to the given question about car loan is option D: $2,315.38; $383.22.
To determine the interest and monthly payment for the car loan, we can use the add-on interest formula:
Total Interest = Principal x Rate x Time
where:
Principal = $16,079 (the amount of the loan)
Rate = 3.6% (the add-on interest rate)
Time = 4 years
Total Interest = $16,079 x 0.036 x 4
Total Interest = $2,315.38
So the total amount of interest on the loan is $2,315.38.
To calculate the monthly payment, we can use the following formula:
Monthly Payment = (Principal + Total Interest) / (Number of Payments)
where:
Principal = $16,079 (the amount of the loan)
Total Interest = $2,315.38 (the total interest on the loan)
Number of Payments = 4 x 12 = 48 (since the loan is for 4 years, and there are 12 months in a year)
Monthly Payment = ($16,079 + $2,315.38) / 48
Monthly Payment = $383.22
Therefore, the amount of interest on the loan is $2,315.38 and the monthly payment for the car loan is $383.22.
To learn more about interest click here
https://brainly.com/question/28792777
#SPJ4
Can someone please tell me the answer to this

Answers
Answer:
Step-by-step explanation:
Hi there!
From the question;
∠E +∠G = 180° ( The sum of opposite angle of cyclic quadrilateral is 180°)
111° + ∠G = 180°
∠G = 180°-111°
Therefore, the measure of angle G is 69°.
Hope it helps!
Select the equation in slope-intercept form for the line through points (5, - 3) and (10, - 2) and is perpendicular to the line described by y = - 5x + 4

Answers
Answer:
y = x/5 - 4
second option is the correct answer.
Step-by-step explanation:
y = -5x+4
y = mx+b
m = -5
Now
Slope of the line perpendicular to a line would be the negative proprtional of the slope of the line.
so,
For the points (5,-3) and (10,-2)
m = 1/5
y = mx + b
or, -3 = 1/5 × x + b
or, -3 = 1/5 × 5 + b
or, -3 = 1+b
so, b = -4
Now,
y = mx+b
or, y = 1/5 × x + (-4)
or, y = x/5 - 4
find the area of a circle with a radius of two either enter an exact answer in terms of pi or use 3.14 for pi and enter your answer as a decimal .
Answers
Answer:
4π
Step-by-step explanation:
Hope this helps. Pls give brainliest.
Answer:
I believe it would be 2 x 3.14= 6.28
( I said 2 because, isn't that the radius of the circle)
Step-by-step explanation:
One day the farm stand sold of the watermelons for $5.75 each. They still have 8 watermelons left. They took in how much money selling watermelons that day?
Answers
Answer:
46
Step-by-step explanation:
first you need to write out your question
then you need to multiply the following numbers (5.75*8)
and that gives you 46.
I hope this is the answer I just get every thing right and I think it is. hofuly it's helping!!