Find the equation of the set of points which are equidistant from the points (1,2,3) and (3,2,−1)
Answers
The equation of for "set-of-points" which are equidistant from points (1, 2, 3) and (3, 2, -1) is x - 2z = 0.
We use "distance-formula" to find equation of "set-of-points" equidistant from points (1, 2, 3) and (3, 2, -1).
The distance formula between two points (x₁, y₁, z₁) and (x₂, y₂, z₂) in three-dimensional space is given by : Distance = √((x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²),
Let us consider a point (x, y, z) that is equidistant from the given points. Using the distance-formula, we can set up the following equations:
√((x - 1)² + (y - 2)² + (z - 3)²) = √((x - 3)² + (y - 2)² + (z + 1)²),
(x - 1)² + (y - 2)² + (z - 3)² = (x - 3)² + (y - 2)² + (z + 1)²
(x² - 2x + 1) + (y² - 4y + 4) + (z² - 6z + 9) = (x² - 6x + 9) + (y² - 4y + 4) + (z² + 2z + 1)
Combining like terms,
We get,
x² - 2x + 1 + y² - 4y + 4 + z² - 6z + 9 = x² - 6x + 9 + y² - 4y + 4 + z² + 2z + 1
Simplifying further,
We have,
x² - 2x + y² - 4y + z² - 6z + 14 = x² - 6x + y² - 4y + z² + 2z + 14
Subtracting x², y², and z² from both sides,
We get,
-2x - 4y - 6z = -6x - 4y + 2z
Combining like-terms,
We get,
-2x + 6x -4y + 4y -6z - 2z = 0
Simplifying further, we have:
4x - 8z = 0
Dividing both sides by 4,
We get:
x - 2z = 0
Therefore, the required equation is x = 2z.
Learn more about Equation here
https://brainly.com/question/24444786
#SPJ4
Related Questions
what is the number of cans that can be packed in a certain carton? the interior volume of this carton is 2,304 cubic inches. the exterior of each can is 6 inches high and has a diameter of 4 inches.
Answers
Answer:
Step-by-step explanation:
volume of each can
=\(\pi\)\(r^{2}\)h
22/7×\(4/2^{2}\)×6
\(\frac{88×6}{7}\)
528/7
The cylinder shown here has a height of 7 centimeters and a radius of 4
a.
What is the area of the base of the cylinder? Express your answer in terms
of
The area of the base is
rcm?
b. How many cubic centimeters of fluid can fill this cylinder? Express your
answer in terms of 77.
The volume of the cylinder is
Tom'
>
Answers
Area=22/4*4^2*7
=616cm
Prove each of the following statements using strong induction. a. Prove that any amount of postage worth 8 cents or more can be made from 3-cent or 5-cent stamps. b. Prove that any amount of postage worth 24 cents or more can be made from 7-cent or 5-cent stamps. c. Prove that any amount of postage worth 12 cents or more can be made from 3-cent or 7-cent stamps.
Answers
a) By strong induction, any amount of postage worth 8 cents or more can be made from 3-cent or 5-cent stamps.
b) By strong induction, any amount of postage worth 24 cents or more can be made from 7-cent or 5-cent stamps.
c) By strong induction, any amount of postage worth 12 cents or more can be made from 3-cent or 7-cent stamps.
a. Prove that any amount of postage worth 8 cents or more can be made from 3-cent or 5-cent stamps.
Base case: For postage worth 8 cents, we can use two 4-cent stamps, which can be made using a combination of one 3-cent stamp and one 5-cent stamp.
Induction hypothesis: Assume that any amount of postage worth k cents or less, where k is greater than or equal to 8, can be made from 3-cent or 5-cent stamps.
Induction step: Consider any amount of postage worth (k+1) cents. Since k is greater than or equal to 8, we can use the induction hypothesis to make k cents using 3-cent or 5-cent stamps. Then, we can add one more stamp to make (k+1) cents. If the last stamp we added was a 3-cent stamp, we can replace it with a 5-cent stamp to get the same value. If the last stamp we added was a 5-cent stamp, we can replace it with two 3-cent stamps to get the same value. Therefore, any amount of postage worth (k+1) cents can be made from 3-cent or 5-cent stamps.
b. Prove that any amount of postage worth 24 cents or more can be made from 7-cent or 5-cent stamps.
Base case: For postage worth 24 cents, we can use three 8-cent stamps, which can be made using a combination of one 7-cent stamp and one 5-cent stamp.
Induction hypothesis: Assume that any amount of postage worth k cents or less, where k is greater than or equal to 24, can be made from 7-cent or 5-cent stamps.
Induction step: Consider any amount of postage worth (k+1) cents. Since k is greater than or equal to 24, we can use the induction hypothesis to make k cents using 7-cent or 5-cent stamps. Then, we can add one more stamp to make (k+1) cents. If the last stamp we added was a 5-cent stamp, we can replace it with two 7-cent stamps to get the same value. If the last stamp we added was a 7-cent stamp, we can replace it with three 5-cent stamps to get the same value. Therefore, any amount of postage worth (k+1) cents can be made from 7-cent or 5-cent stamps.
c. Prove that any amount of postage worth 12 cents or more can be made from 3-cent or 7-cent stamps.
Base case: For postage worth 12 cents, we can use one 3-cent stamp and three 3-cent stamps, which can be made using a combination of two 7-cent stamps.
Induction hypothesis: Assume that any amount of postage worth k cents or less, where k is greater than or equal to 12, can be made from 3-cent or 7-cent stamps.
Induction step: Consider any amount of postage worth (k+1) cents. Since k is greater than or equal to 12, we can use the induction hypothesis to make k cents using 3-cent or 7-cent stamps. Then, we can add one more stamp to make (k+1) cents. If the last stamp we added was a 3-cent stamp, we can replace it with two 7-cent stamps to get the same value. If the last stamp we added was a 7-cent stamp, we can replace it with one 3-cent stamp and two 7-cent stamps to get the same value. Therefore, any amount of postage worth (k+1) cents can be made from 3
Learn more about strong induction
brainly.com/question/30692296
#SPJ4
Rational number between 3.623623 and 0.484848
Answers
Answer:
1
Step-by-step explanation:
A rational number between 3.623623 and 0.484848 is 1.
Answer:
Remember: rational numbers are numbers that can be written as fractions and decimals that either terminate or repeat. Here are some rational numbers:
0.5, 3/4, 1, 1.5...3, 3.5
Step-by-step explanation:
BRAINLIEST, PLEASE!
Meg plotted the graph below to show the relationship between the temperature of her city and the number of people at a swimming pool:
Main title on the graph is Swimming Pool Population. Graph shows 0 to 30 on x axis at increments of 5 and 0 to 12 on y axis at increments of 1. The label on the x axis is Temperature in degree C, and the label on the y axis is Number of People at the Pool. Dots are made at the ordered pairs 2.5, 1 and 5, 2 and 7.5, 2 and 7.5, 3 and 7.5, 4 and 10, 5 and 10, 6 and 12.5, 6 and 15, 7 and 15, 8 and 17.5, 5 and 17.5, 7 and 20, 9 and 22.5, 7 and 22.5, 9 and 25, 11 and 27.5, 12.
Part A: In your own words, describe the relationship between the temperature of the city and the number of people at the swimming pool. (5 points)
Part B: Describe how you can make the line of best fit. Write the approximate slope and y-intercept of the line of best fit. Show your work, including the points that you use to calculate slope and y-intercept. (5 points)
Answers
Answer:
Step-by-step explanation:
Part A: Based on the given graph, we can observe that as the temperature of the city increases, the number of people at the swimming pool generally tends to increase as well. This suggests a positive correlation between temperature and the pool's population. In other words, when it gets hotter, more people are likely to visit the swimming pool. The relationship is not strictly linear, but it shows a general trend of increasing pool population with increasing temperature.
Part B: To determine the line of best fit, we can calculate the approximate slope and y-intercept using the given data points. Let's select two points from the data, such as (2.5, 1) and (12, 12):
Slope (m) = (change in y) / (change in x)
= (12 - 1) / (12 - 2.5)
= 11 / 9.5
≈ 1.16
To find the y-intercept (b), we can choose one of the points and substitute the values into the slope-intercept form (y = mx + b). Let's use the point (2.5, 1):
1 = 1.16 * 2.5 + b
1 = 2.9 + b
b ≈ -1.9
Therefore, the approximate slope of the line of best fit is 1.16, and the approximate y-intercept is -1.9.
the sum of two numbers is 30. when is the product of the first number multiplied by the square of the second number maximum
Answers
The two numbers required to solve the following problem are, 13.3 and 6.7
What is Derivative?
The derivative of a function of a real variable in mathematics describes the sensitivity of the function value to a change in its argument. Calculus relies heavily on derivatives.
Solution:
Let the ture positive numbers be x,(x,y>0)
x + y = 20 -------- Given
We need to maximise \(xy^{2}\)
x = 20 - y
f(y) = (20 - y)*\(y^{2}\)
f(y) = 20\(y^{2}\) - \(y^{3}\)
f'(y) = 0
On differentiating:
f'(y) = 40y - 3\(y^{2}\)
0 = 40 - 3y
y = 13.3
x = 6.7
To learn more about Derivatives from the given link
https://brainly.com/question/28376218
#SPJ4
Which phrase best describes the translation from the graph y=6x^2 to the graph of y=6 (x+1)^2?
6 units right
6 units left
1 unit right
1 unit left
Answers
Answer:
1 unit left
Step-by-step explanation:
Here, we want to get the kind of transformation applied
From the given equations, we can see that the value 1 being added to 1 in the second equation is the difference
What this mean is that we have an issue with the x value
For x to move to x + 1, there is a translation to the tune of 1 unit in the left direction
What is the area of this figure?
Enter your answer in the box.
___ units²

Answers
Step-by-step explanation:
we can split the figure into 2 trapezium
\(area \: of \: trapeium = ( \frac{a + b}{2} )(h) \)
area of 1st trapezium
= (7+3/2)(4)
= (5)(4)
= 20 units^2
area of 2nd trapezium
= (3+5/2)(2)
= (4)(2)
= 8 units^2
total area of trapezium
= 20+8
= 28 units^2
The area of the figure is a sum of two trapezoids as A = 28 units²
Given data ,
Let the area of the figure be represented as A
Now , the area of the first trapezoid be represented as T₁
The area of the first trapezoid be represented as T₂
The area of the Trapezoid is given by
Area of Trapezoid = ( ( a + b ) h ) / 2
where , a = shorter base of trapezium
b = longer base of trapezium
h = height of trapezium
So, T₁ = [ ( 7 + 3 )/2 ] x 4
T₁ = 10 x 2
T₁ = 20 units²
And , T₂ = [ ( 3 + 5 )/2 ] x 2
T₂ = 4 x 2
T₂ = 8 units²
where A = 20 + 8 = 28 units²
Hence , the area of the figure is A = 28 units²
To learn more about trapezoid click :
https://brainly.com/question/12221769
#SPJ1
In the picture below, a fraction of the piles are red?

Answers
There are 9 piles and only one is red
(1 point)
5. If m ZAOC = 85°, mZBOC = 2x + 10, and m ZAOB = 4x – 15, find the degree measure of
ZBOC and ZAOB. The diagram is not to scale.
<
G
Om ZBOC = 30°; m ZAOB = 55°
Om ZBOC = 40°; m ZAOB = 45°
Om ZBOC = 45°: m ZAOB = 40°
Om ZBOC = 55°; m ZAOB = 30°

Answers
Is continuous 0.23 rational irrational 5 star to who ever helps
Answers
Answer:
yessssssssssssssssssssssssssssss
What is the constant of this polynomial? 2x3 - 8x2 3x - 7
Answers
The constant term of the polynomial \(2x^3 - 8x^2+ 3x -7\\\) is -7
What is a polynomial?
At first, it is important to know about algebraic expression.
Algebraic expression consist of variables and numbers connected with addition, subtraction, multiplication and division sign.
A mathematical expression of the form \(a_0 + a_1x + a_2x^2 + .... + a_nx^n, (a_n \neq 0)\) is called a polynomial of degree n
Here the polynomial is
\(2x^3 - 8x^2+ 3x -7\\\)
There is no variable associated with the term -7
So the constant in this polynomial is -7
To learn more about polynomial, refer to the link-
https://brainly.com/question/2833285
#SPJ4
Correct Question
What is the constant of this polynomial?
\(2x^3 - 8x^2+ 3x -7\\\)
What is the area of the wreck site?
Answers
Answer:
where is the photo?
Step-by-step explanation:
Where is the photo, I need you to give me more details so i can officially answer your question, thank you :)
3. A leaking tap drips water at 0,5 ml/sec. Convert this rate to l/h.
Answers
Answer: 1.8 L/h
Step-by-step explanation:
To convert the rate of water dripping from a tap from millilitres per second (ml/sec) to litres per hour (L/h), we need to use conversion factors.
Step 1:
First, let's convert the rate from millilitres per second to litres per second.
There are 1000 millilitres in a litre, so we can divide the rate in millilitres per second by 1000 to get the rate in litres per second:
\(\LARGE \boxed{\textsf{0.5 ml/sec $\div$ 1000 = 0.0005 L/sec}}\)
Step 2:
We can convert the rate from litres per second to litres per hour. There are 3600 seconds in an hour, so we can multiply the rate in litres per second by 3600 to get the rate in litres per hour:
\(\LARGE \boxed{\textsf{0.0005 L/sec $\times$ 3600 = 1.8 L/h}}\)
Therefore, the rate of water dripping from the tap is 1.8 L/h.
----------------------------------------------------------------------------------------------------------
PLS HELP
The length of the tunnel is 350 miles. If 1 inch represents 50 miles, what is the length of the scale drawing of the tunnel? Be sure to include units!
Answers
Answer:
7 inches
Step-by-step explanation: Every 1 inch = 50 miles. So every 50 miles of tunnel is 1 inch in a scale drawing. 350miles/50 miles=7 inches.
The scale drawing is 7 inches.
Answer:
7 inches
Step-by-step explanation:
Complete the conversion. Enter your answer in the box.
40 cm =
m
Answers
Answer:
40 cm = 0.4 m
How do I find the missing endpoint? Detailed explanation…I need to know how to do this.

Answers
======================================================
Explanation:
Let's focus on only the x coordinates for now.
The endpoint has x coordinate 6 and the midpoint's x coordinate is 4.5
The other endpoint's x coordinate is unknown. I'll call this P. I'm tempted to use x, but I want to avoid being this repetitious using x.
What happens is that we add up the two endpoint values, and divide by 2, to get the midpoint value. We'll use algebra to solve for P.
So,
midpoint = (endpoint1 + endpoint2)/2
4.5 = (6 + P)/2
4.5*2 = 6+P
9 = 6+P
P = 9-6
P = 3
This mystery endpoint has 3 as its x coordinate.
---------------------------
Now onto the y coordinate. We'll use the same idea as the last section.
The y coordinates are...
-2 for the first endpoint-2.5 for the midpointQ for the other endpoint, aka some unknown valueSo,
(endpoint1 + endpoint2)/2 = midpoint
(-2 + Q)/2 = -2.5
-2+Q = 2(-2.5)
-2+Q = -5
Q = -5 + 2
Q = -3
The y coordinate for the other endpoint is -3
---------------------------
To wrap everything up, we found that the other endpoint has x and y coordinates of 3 and -3 in that exact order.
Therefore, the missing endpoint is (3, -3)
If you were to apply the midpoint formula on (6,-2) and (3,-3) then you would find the midpoint is (4.5, -2.5). This will help confirm the answer.
Check out the diagram below for visual confirmation. This part is optional but I find it's handy to have. The diagram shows point A in blue as the given endpoint and point C in black as the given midpoint. The red point B is the answer we're after, aka that mystery endpoint.

Help me please i will give brainliest.
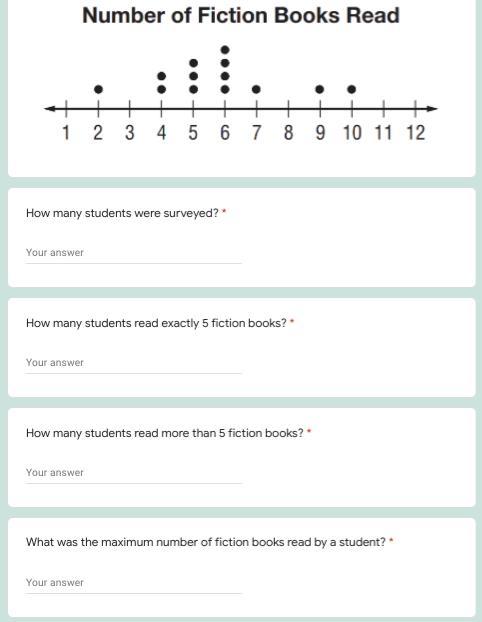
Answers
Answer:
1) 13 Students were surveyed
2) 3 students
3) 7 Students
4) 10 Books
Pls mark brainliest
Answer:
13 students were surveyed
3 students read 5 fiction books
7 students read more than 5 fiction books
The maximum number was 10
Step-by-step explanation:
Hope this helps
-Unbrand-
Sadly even though I answered first I didn't get any credit. Quite sickening.
A TV has a listed price of $788.99 before tax. If the sales tax rate is 8.75%, find the total cost of the TV with sales tax included. Round your answer to the nearest cent, as necessary.
Answers
Answer:
$858.02
Step-by-step explanation:
Take $788.99 times 8.75% = 69.03 this is the amount of tax
Add 788.99 and 69.03 = 858.02
Answer:
the answer would be $858.03
What is the width of the loss cone (in degrees) at a radius of \( 25,000 \mathrm{~km} \) ?
Answers
To calculate the width of the loss cone at a radius of 25,000 km, we can use trigonometry by taking the arctangent of the ratio of the width to the radius.
The loss cone is a concept used in plasma physics to describe the region of particles' pitch angles that are vulnerable to being lost or escaping from a confined plasma system. The width of the loss cone can be calculated using trigonometry.At a given radius of \( 25,000 \) km, we can consider a line connecting the center of the system to the point on the loss cone. This line represents the magnetic field line. The width of the loss cone can be determined by the angle formed between this line and the tangent to the loss cone.
To calculate this angle, we need the radius of the system, which is \( 25,000 \) km. Assuming a spherical system, we can consider the tangent to the loss cone as a line perpendicular to the radius. In this case, we have a right triangle where the radius is the hypotenuse.Using basic trigonometry, we can determine the angle by taking the inverse tangent of the ratio of the width of the loss cone (opposite side) to the radius (hypotenuse). The width of the loss cone will be the arctangent of the ratio.
Therefore, To calculate the width of the loss cone at a radius of 25,000 km, we can use trigonometry by taking the arctangent of the ratio of the width to the radius.
To learn more about radius click here
brainly.com/question/32344902
#SPJ11
Calculate the total charge in the device at t = 1 s, assuming q(0) = 0. the total charge in the device at t = 1 s is:_________
Answers
A. The total charge in the device at t = 1 s is 28(1 + e⁻²¹) × 10⁻³ mC.
B. The power consumed by the device at t = 1 s is 27 sin(44) × 28(1 + e⁻²¹) mW.
How did we get the values?To calculate the total charge in the device at t = 1 s, we need to integrate the current over time.
Given:
v(0) = 27 sin(44) V
i(0) = 28(1 + e⁻²¹) mA
We'll convert the current to amperes for consistency:
i(0) = 28(1 + e⁻²¹) × 10^(-3) A
We integrate the current from t = 0 to t = 1 s to find the total charge:
q(t) = ∫[0 to t] i(t') dt'
Since q(0) = 0, we can write:
q(t = 1) = ∫[0 to 1] i(t') dt'
Let's perform the integration:
q(t = 1) = ∫[0 to 1] 28(1 + e⁻²¹) × 10⁻³ dt'
= 28(1 + e⁻²¹) × 10⁻³ ∫[0 to 1] dt'
= 28(1 + e⁻²¹) × 10⁻³ [t'] [0 to 1]
= 28(1 + e⁻²¹) × 10⁻³ (1 - 0)
= 28(1 + e⁻²¹) × 10⁻³ mC
Therefore, the total charge in the device at t = 1 s is 28(1 + e⁻²¹) × 10⁻³ mC.
B. To calculate the power consumed by the device at t = 1 s, use the formula:
P(t) = v(t) × i(t)
Given v(0) = 27 sin(44) V and i(0) = 28(1 + e⁻²¹) mA, we need to evaluate v(t) and i(t) at t = 1 s:
v(t = 1) = 27 sin(44)
i(t = 1) = 28(1 + e⁻²¹)
Now we can calculate the power:
P(t = 1) = v(t = 1) × i(t = 1)
= 27 sin(44) × 28(1 + e⁻²¹)
Therefore, the power consumed by the device at t = 1 s is 27 sin(44) × 28(1 + e⁻²¹) mW.
learn more about charge and power: https://brainly.com/question/874116
#SPJ4
The complete question goes thus:
The voltage v1) across a device and the current i(t) through it are (0) = 27 sin(44) V and (0) = 28(1 + e-21) mA.
Calculate the total charge in the device at t = 1 s, assuming q(0) = 0. The total charge in the device at t = 1 s is ___ mC.
Calculate the power consumed by the device at t = 1 s. The power consumed by the device at t = 1 s is ___ mW.
What is 2x-y <4 graphed on a graph
Answers
Answer:
y>2x-4
y int = -4
over 2 right 1 (like staircase)
The line is dotted and shade to the left of graph
Step-by-step explanation:
Please answer this question now in two minutes

Answers
Answer:
Ray WV and Ray WX.
Step-by-step explanation:
A ray is a line that has a fixed starting point, but no end points. It extends infinitely. You usually list points based on the way it is facing.
Hope this helps!
Answer: Ray VW and Ray XW
Step-by-step explanation:
The points V and W have a distance between each other, so that is a line.
The points X and W have a distance between each other, so that is a line.
Since W is the vertex, I’d put it as the 2nd letter in each ray.
The ray sign is ==>
Ramona is counting the posts between mile makers on the highway. In 1 mile, she counts 33 posts. If the posts are evenly spaced, how many feet apart are they? (1 mile = 5,280 feet)
Answers
Answer:
160feet
Step-by-step explanation:
5280 divided by the number of posts
count in mile= 33 posts.
to find:the distance between the posts.
solution:1 mile= 5280ft
distance= 5280/33
=160ft
so the distance between the posts are 160ft.
24.7% of the products in the local shop are specialty soaps. 76% of those soaps are made with fresh herbs. if there are 350 bars of specialty soap in the shop, approximately how many of them are not made with fresh herbs? round your answer up to nearest whole number
Answers
we know that 76% of the specialty soaps are made with fresh herbs, and we also know that there are a total of 350 specialty soap bars, so how many are made with fresh herbs? well, just 76% of those 350
\(\begin{array}{|c|ll} \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{76\% of 350}}{\left( \cfrac{76}{100} \right)350}\implies 266\)
The graph of f(x) and g(x) are shown below. How many solutions does the system of equations have?
Click pic to see whole problem

Answers
Answer:
Step-by-step explanation:
Solving systems of equations gives the points of intersection when the equations are graphed.
The answer is 3.
In AKLM, KL || NO. Given that MN=15, ML=48, and MO=20, find MK.
MK =

Answers
The length of MK is given as follows:
MK = 36.
What are similar triangles?Similar triangles are triangles that share these two features presented as follows:
Congruent angle measures.Proportional side lengths.The similar triangles for this problem are given as follows:
MNO and MKL.
Hence the proportional relationship for the side lengths is given as follows:
15/MK = 20/48
Applying cross multiplication, the length MK is given as follows:
20MK = 15 x 48
MK = 15 x 48/20
MK = 36.
More can be learned about similar triangles at brainly.com/question/14285697
#SPJ1
Consider the equation x – 8 = 4 – 2x.
The picture shows the graphs of y = x – 8 and y = 4 – 2x.
Which statement is true?
Think Through Math question
!!!GIVING 20 POINTS!!!
Answers
From interpretation of the given graph, we can say that the equation given as ¹/₂(2x + 8) = x + 4 has no solution
How to find the solution to graphical equation?We are given the equation as;
¹/₂(2x + 8) = x + 4
Now, expanding the bracket using distributive property gives us;
x + 4 = x + 4
Since left hand side is equal to right hand side, then it means that the equation has no solution.
Now, looking at the given graph, we can see that the line of both equations overlap each other which means they don't intersect to provide a solution.
Read more about Graph Solution at; https://brainly.com/question/4025726
#SPJ1
Find the perimeter of the triangle whose vertices are the following specified points in the plane.
(1,−5), (4,2) and (−7,−5)
Answers
Using the distance formula, we find:
- The distance between (1,-5) and (4,2) is sqrt[(4-1)^2 + (2-(-5))^2] = sqrt[3^2 + 7^2] = sqrt[58].
- The distance between (4,2) and (-7,-5) is sqrt[(-7-4)^2 + (-5-2)^2] = sqrt[(-11)^2 + (-7)^2] = sqrt[170].
- The distance between (-7,-5) and (1,-5) is sqrt[(1-(-7))^2 + (-5-(-5))^2] = sqrt[8^2] = 8.
Adding these distances together, we get:
sqrt[58] + sqrt[170] + 8
This is the perimeter of the triangle. We can simplify it by leaving it in terms of radicals, or by using a calculator to get a decimal approximation.
use the empirical rule to answer the following question. if the average age of retirement for the entire population in a country is 64 years and the distribution is normal with a standard deviation of 3.5 years, what is the approximate age range in which 95% of people retire?
Answers
The empirical rule, also known as the 68-95-99.7 rule, is a statistical guideline that applies to data with a normal distribution. It states that approximately 68% of the data falls within one standard deviation of the mean, 95% falls within two standard deviations, and 99.7% falls within three standard deviations.
In this case, we are given that the average age of retirement for the entire population in a country is 64 years, with a standard deviation of 3.5 years.
To find the approximate age range in which 95% of people retire, we can use the empirical rule. Since 95% falls within two standard deviations, we need to find the range that is two standard deviations away from the mean.
Step-by-step:
1. Find the range for two standard deviations:
- Multiply the standard deviation (3.5 years) by 2.
- 2 * 3.5 = 7 years
2. Determine the lower and upper limits:
- Subtract the range (7 years) from the mean (64 years) to find the lower limit:
- 64 - 7 = 57 years
- Add the range (7 years) to the mean (64 years) to find the upper limit:
- 64 + 7 = 71 years
Therefore, on the basis of the empirical rule, approximately 95% of people retire between the ages of 57 and 71 years, based on the given average age of retirement (64 years) and standard deviation (3.5 years).
To know more about standard deviation visit:
https://brainly.com/question/475676
#SPJ11