Find the exact surface area of the resulting surface y = √4-x² on the interval [-1, 1] rotated about the X-axis.
Answers
The exact surface area of the solid generated by rotating the curve y = √(4-x²) is (8/3)π².
How to find the surface area of the solid generated by rotating the curve y?To find the surface area of the solid generated by rotating the curve y = √(4-x²) about the x-axis over the interval [-1, 1], we can use the formula:
S = 2π ∫[a,b] y(x)√(1 + (y'(x))²) dx
where y(x) = √(4-x²) and y'(x) = (-x) / √(4-x²)
Substituting these values in the formula, we get:
S = 2π ∫[-1,1] √(4-x²)√(1 + ((-x) / √(4-x²))²) dx
Simplifying the expression under the radical, we get:
S = 2π ∫[-1,1] √(4-x²)√(1 + x²/(4-x²)) dx
Simplifying further, we get:
S = 2π ∫[-1,1] √(16/(4-x²)) dx
S = 4π ∫[-1,1] √(1/(1-(x/2)²)) dx
Now let's use the substitution x/2 = sin(t) and dx = 2cos(t)dt to convert the integral into a form that can be evaluated using standard trigonometric integrals. Substituting these values, we get:
S = 4π ∫[-π/6,π/6] √(1/(1-sin²(t))) 2cos(t) dt
Simplifying the expression under the radical, we get:
S = 4π ∫[-π/6,π/6] sec(t) 2cos(t) dt
Simplifying further, we get:
S = 8π ∫[-π/6,π/6] dt
S = 8π (π/3)
S = (8/3)π²
Therefore, the exact surface area of the solid generated by rotating the curve y = √(4-x²) about the x-axis over the interval [-1, 1] is (8/3)π².
Learn more about surface area
brainly.com/question/29298005
#SPJ11
Related Questions
7th grade math
2 If 40 is decreased by 80%, what is the new amount?
Answers
Answer:
32
Step-by-step explanation:
Answer: i think 3900
Step-by-step explanation:
the horizontal, continuous lintel on a classical building supported by columns is called a stylobate. T/F
Answers
The statement "the horizontal, continuous lintel on a classical building supported by columns is called a stylobate" is False.
The horizontal, continuous lintel on a classical building supported by columns is called an entablature, while the stylobate is the platform on which the columns stand.
In classical architecture, the entablature is the horizontal, continuous lintel that rests on top of the columns and consists of three parts: the architrave (the bottom layer), the frieze (the middle layer), and the cornice (the top layer). The entablature helps to unify the columns and create a sense of continuity across the facade of the building.
The stylobate, on the other hand, is the platform or base upon which the columns stand, and is usually elevated above ground level. Together, the stylobate and entablature form the colonnade, a defining feature of classical architecture.
Learn more about classical architecture :
https://brainly.com/question/15155708
#SPJ4
rack heights vary from a few rack units to many rack units. the most common rack heights are 24u and 42u. how tall is a 24u rack?
Answers
A 24U rack is approximately 44.5 inches (113.03 cm) tall.
What is Expression in math ?
An expression is made up of one or more integers or variables, as well as one or more operations.
The "U" unit in a rack height refers to unit of measurement for the height of equipment in a standard 19-inch server rack.
1U is equal to 1.75 inches (4.45 cm)
so, 24U is equal to 24 * 1.75 inches = 42 inches (106.68 cm).
However, in practice, the height of a 24U rack is typically slightly taller to account for the height of the mounting brackets and other hardware.
Hence, A 24U rack is approximately 44.5 inches (113.03 cm) tall.
To know more about Expressions visit,
https://brainly.com/question/1859113
#SPJ4
Please help me please help me please help me please help me please me please help me

Answers
The value of x is 14
HJ = 79
JK = 50
Calculating length of line segmentsFrom the question, we are to determine the value of x and the length of each segment
From the given information,
Point J is between points H and K
Then, we can write that
HJ + JK = KH
Also, from the given information,
HJ = 6x - 5
JK = 4x - 6
KH = 129
6x - 5 + 4x - 6 = 129
6x + 4x -5 -6 = 129
10x - 11 = 129
10x = 129 + 11
10x = 140
x = 140/10
x = 14
∴ The value of x is 14
HJ = 6x - 5
∴ HJ = 6(14) - 5
HJ = 84 - 5
HJ = 79
Also,
JK = 4x - 6
JK = 4(14) - 6
JK = 56 - 6
JK = 50
Hence,
The value of x is 14
HJ = 79
JK = 50
Learn more on Calculating length of line segments here: https://brainly.com/question/2264333
#SPJ1
Joe and chris each have a lawn mowing business. Joe charges 40 to mow 2 acres. Chris charges 30 to mow 1. 2 acres. Who charges more per acre? What is the answer
Answers
Joe charges more per acre than Chris. Joe charges $20 per acre and Chris charges $30 per acre.
Starting a lawn mowing business can be a profitable and rewarding venture if you have the right tools, skills, and strategies in place.Research your local area to determine the demand for lawn mowing services, the competition, and the going rate for services. This will help you determine whether starting a lawn mowing business is a viable option in your area.Create a business plan that outlines your goals, target market, services, pricing, and marketing strategies. This will help you stay organized and focused as you launch and grow your business.Check with your local government to find out what licenses and permits you need to start a lawn mowing business in your area.Therefore,from the given information Joe charges more per acre.
For such more questions on lawn mowing business:
brainly.com/question/29300074
#SPJ11
Multiply and simplify if possible - radical functions. Thank you!
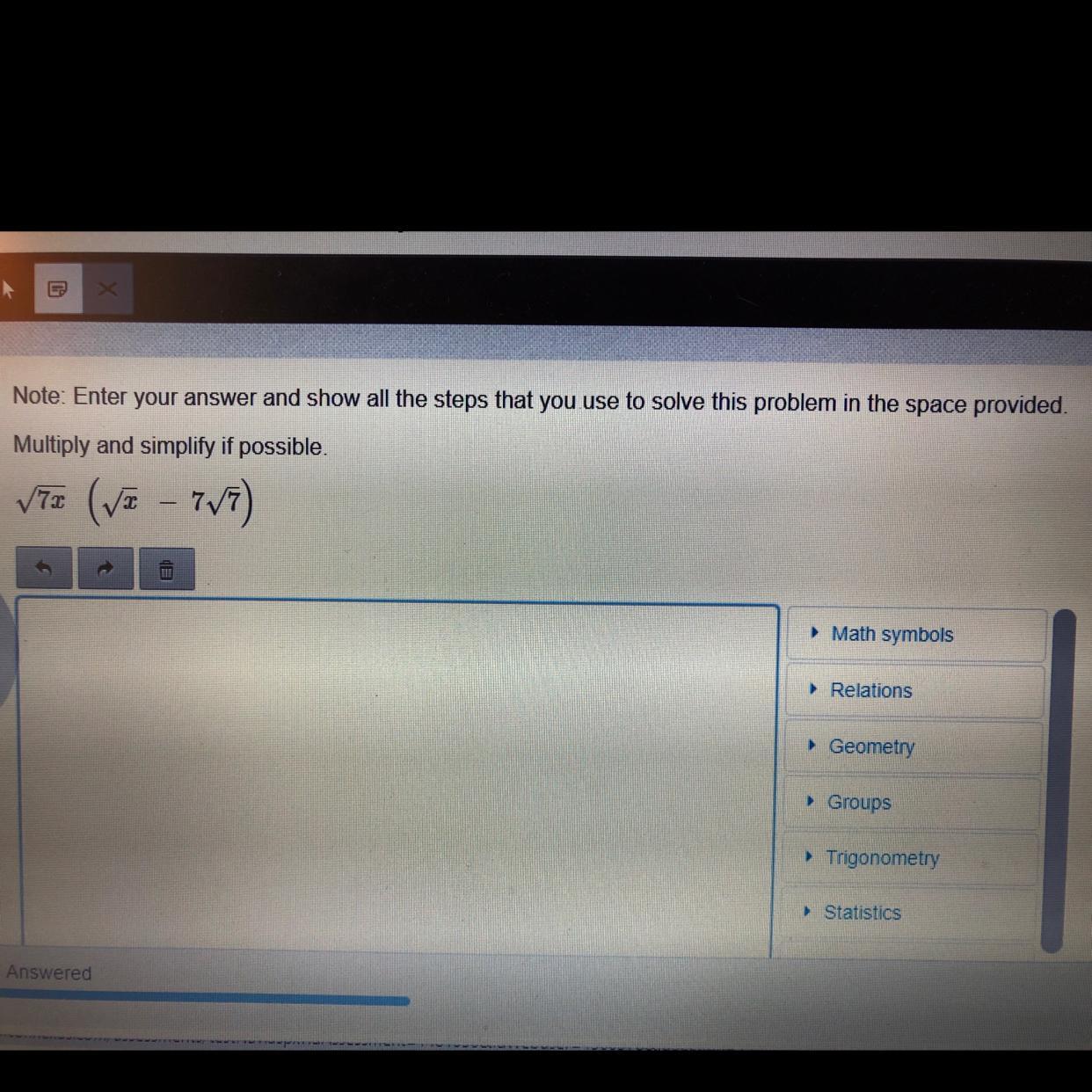
Answers
We want to simplify the following expression
\(\sqrt{7x}(\sqrt{x}+7\sqrt{7})\)First, we can apply the distributive rule to rewrite this product
\(\sqrt{7x}(\sqrt{x}+7\sqrt{7})=(\sqrt{7x})(\sqrt{x})+(\sqrt{7x})(7\sqrt{7})\)Then, using the following property
\(\sqrt{x}\cdot\sqrt{y}=\sqrt{x\cdot y}\)we can rewrite our expression as
\((\sqrt{7x})(\sqrt{x})+(\sqrt{7x})(7\sqrt{7})=\sqrt{7x\cdot x}+7\sqrt{7x\cdot7}\)We can remove the squared terms out of the root
\(\sqrt{7x\cdot x}+7\sqrt{7x\cdot7}=x\sqrt{7}+7\cdot7\sqrt{x}=x\sqrt{7}+49\sqrt{x}\)and this is our answer.
\(\sqrt{7x}(\sqrt{x}+7\sqrt{7})=x\sqrt{7}+49\sqrt{x}\)36 (highest)POINTS PLS ANSWER ASAP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Then, inches to foot (12 inches in 1 foot)
So, 140/12 which is 11 2/3 feet
Now 11 2/3 * 2.50 for each foot is 29.16 (rounded down, 29$) (not sure if this is right btw)
Once a month, volunteers from the Green Sea Club clean up litter at the beach. Last month, the volunteers picked up 8 pounds of trash in 4 hours. This month, the same group of volunteers will spend 3 hours picking up trash.
If they pick up trash at the same rate, how many pounds of trash should the volunteers pick up this month?
Answers
Answer:
Step-by-step explanation:
8 pounds.... 4hours
x pounds.... 3 hours
x=3 ×8 :4
x=24 :4
x=6 pounds of trash
The number of pounds of trash should the volunteers pick up this month is 6.
Calculation of the number of pounds:Since Last month, the volunteers picked up 8 pounds of trash in 4 hours. This month, the same group of volunteers will spend 3 hours picking up trash.
So here we can do
x=3 ×8 :4
x=24 :4
x=6
Hence, The number of pounds of trash should the volunteers pick up this month is 6.
Learn more about number here: https://brainly.com/question/24475075
three events e, f , and g cannot occur simultaneously. further it is known that p(e∩f) = p(f ∩g) = p(e∩g) = 1/3. can you deter- mine p(e)?
Answers
After solving for p(e∩f) = p(f ∩g) = p(e∩g) = 1/3 the value of p(e) (probability of e event occurs) is 1/3.
Let's start by using the inclusion-exclusion principle:
p(e ∪ f ∪ g) = p(e) + p(f) + p(g) - p(e ∩ f) - p(f ∩ g) - p(e ∩ g) + p(e ∩ f ∩ g)
Since e, f, and g cannot occur simultaneously, we have:
p(e ∩ f ∩ g) = 0
Substituting the given values of p(e ∩ f), p(f ∩ g), and p(e ∩ g), we have:
p(e ∪ f ∪ g) = p(e) + p(f) + p(g) - 1/3 - 1/3 - 1/3
p(e ∪ f ∪ g) = p(e) + p(f) + p(g) - 1/3
Since e, f, and g are mutually exclusive, we have:
p(e ∪ f ∪ g) = p(e) + p(f) + p(g)
Substituting this into the previous equation, we get:
p(e) + p(f) + p(g) = p(e) + p(f) + p(g) - 1/3
Simplifying, we get:
1/3 = p(e)
Therefore, the probability of event e is 1/3.
for such more question on probability
https://brainly.com/question/24756209
#SPJ4
How do i make 2 ( x + 3 ) into a no solution problem?
Answers
Answer:
By making x = -3
Step-by-step explanation:
If X was -3 then -3 plus 3 equals 0, and 2 multiplied by 0 is 0, so the problem will have no solution.
Hope this helps! :)
Ajar contains 4 red marbles, 2 white marbles, and 6 blue marbles. Two marbles are randomly selected from the jar with replacement. Find the following probabilities. Enter your answers as reduced fractions. 5(a) A red marble and then a blue marble is randomly selected. 5(b) A white marble and then a red marble is randomly selected
Answers
The probability of getting a red marble and then a blue marble is 1/6 and the probability of getting a white marble and then a red marble is 1/18.
The given jar has 4 red marbles, 2 white marbles, and 6 blue marbles.
Two marbles are randomly selected from the jar with replacement.
The probabilities for the selection of marbles with specific color is given below:
Probability of selecting red marble = 4/12
Probability of selecting white marble = 2/12
Probability of selecting blue marble = 6/12
(a) We are to find the probability of selecting a red marble and then a blue marble.
The selection is with replacement.
Therefore, the probability of selecting a red marble and then a blue marble is:
P(Red and then Blue) = P(Red) × P(Blue)
= (4/12) × (6/12)
= 1/6
(b) We are to find the probability of selecting a white marble and then a red marble.
The selection is with replacement.
Therefore, the probability of selecting a white marble and then a red marble is:
P(White and then Red) = P(White) × P(Red)
= (2/12) × (4/12)
= 1/18
Therefore, the probabilities for the following selections are:
Probability of selecting a red marble and then a blue marble = 1/6 and the probability of selecting a white marble and then a red marble = 1/18.
Learn more about probability:
https://brainly.com/question/24756209
#SPJ11
a)Probability of selecting a red marble and then a blue marble is 1/6
b)Probability of selecting a white marble and then a red marble is 1/18
P(A and B) = P(A) * P(B)
where P(A) is the probability of event A happening and P(B) is the probability of event B happening.
(a) To find the probability of selecting a red marble and then a blue marble, we can use the formula:
P(red, then blue) = P(red) * P(blue)
The probability of selecting a red marble on the first draw is 4/12 (since there are 4 red marbles out of a total of 12 marbles). The probability of selecting a blue marble on the second draw is also 6/12 (since we are replacing the first marble, so there are still 6 blue marbles out of a total of 12 marbles). So:
P(red, then blue) = (4/12) * (6/12) = 1/6
So the probability of selecting a red marble and then a blue marble is 1/6.
(b) To find the probability of selecting a white marble and then a red marble, we can use the same formula:
P(white, then red) = P(white) * P(red)
The probability of selecting a white marble on the first draw is 2/12 (since there are 2 white marbles out of a total of 12 marbles). The probability of selecting a red marble on the second draw is 4/12 (since we replaced the first marble, so there are still 4 red marbles out of a total of 12 marbles). So:
P(white, then red) = (2/12) * (4/12) = 1/18
So the probability of selecting a white marble and then a red marble is 1/18.
learn more about 'probability':https://brainly.com/question/31265760
#SPJ11
y is inversely proportional to √x
y = 9 when x = 16
a) An equation connecting y and x can be written in the form y=k/ √x
Work out the value of k.
k=
b) Work out the value of y when x = 25
y =
c) Work out the value of x when y = 4.5
Answers
Answer:
k=36; y=1.44; x=8
Step-by-step explanation:
a) y= k/square root of x
9=k/square root of 16
9=k/4
9×4= (k/4)×4
therefore k=36
b) Using k...
y=36/25
therefore y=1.44
c) 4.5=36/x
4.5×(x)= (36/x)×(x)
4.5x=36
therefore x=8
The volume of a cone is 88 pi cubic feet. Its height is 8 feet. Fatima is finding the radius of the cone. Her work is shown below.
V = one-third pi r squared h. Step 1: 88 pi = one-third pi r squared (8). Step 2: 88 pi = StartFraction 8 Over 3 EndFraction pi r squared. Step 3: StartFraction 8 Over 3 EndFraction (88) = r squared. Step 4: 234.7 = r squared. Step 5: 15.3 = r.
What is Fatima’s error?
In step 4, Fatima did not find the correct value of StartFraction 8 Over 3 EndFraction (88).
In step 2, Fatima should not have multiplied One-third and 8.
In step 3, Fatima did not multiply 88 by the reciprocal of StartFraction 8 Over 3 EndFraction.
In step 1, Fatima did not substitute the correct value for the height in the formula.
Answers
Answer:
c
did it on edg:D
mark brainliest please need it for a new rank
Answer:
C or "In step 3, Fatima did not multiply 88 by the reciprocal of 8/3"
Step-by-step explanation:
Evaluate The Following Expression When X= -5
-4+3-(2x+5)²
Answers
Answer:
-26
Step-by-step explanation:
sub in the x value
-4+3-(2(-5)+5)^2
-4+3-(-10+5)^2
-4+3-(5)^2
-1-25
-26
twenty five people, consisting of women and men are lined up in a random order. find the probability that the ninth woman to appear is in position 17. that is, find the probability there are women in positions thru and a woman in position 17
Answers
The probability that the ninth woman to appear is in position 17 is about 5.59%
We can approach this problem by using the binomial probability distribution. Let X be the number of women among the first 16 people in the line. Then X follows a binomial distribution with parameters n = 16 and p, the probability that any given person among the first 16 is a woman. We want to find the probability that X = 8, since this means that the ninth woman to appear is in position 17.
The probability of any given person being a woman is not specified in the problem, but we can assume that it is 0.5 for simplicity. Therefore, p = 0.5, and we can use the binomial probability formula:
P(X = k) = (n choose k) * p^k * (1-p)^(n-k)
where (n choose k) is the binomial coefficient, which gives the number of ways to choose k items from a set of n items. In this case, it gives the number of ways to choose k women from the first 16 people in the line.
Using this formula with n = 16 and k = 8, we get:
P(X = 8) = (16 choose 8) * 0.5^8 * 0.5^8
= 12870 * 0.00390625
= 50.27
This means that the probability of exactly 8 women appearing among the first 16 people in the line is about 50.27%.
Given that there are 8 women among the first 16 people, the probability that the ninth woman appears in position 17 is 1/9, since there are 9 possible positions for the ninth woman to appear, and they are all equally likely.
Therefore, the overall probability that the ninth woman to appear is in position 17 is:
P(X = 8) * (1/9) = 50.27% * (1/9) = 5.59%
Learn more about binomial probability here: brainly.com/question/24756209
#SPJ4
a merchant blends tea that sells for $3 a pound with tea that sells for $2.75 a pound to produce 80 lb of mixture that sells for $2.90 a pound. how many pounds of each type of tea does the merchant use in the blend?
Answers
the merchant uses 48 pounds of the $3 tea and 32 pounds of the $2.75 tea in the blend.
To determine the amount of each type of tea used in the blend, we can set up a system of equations based on the given information. Let's assume x pounds of the $3 tea are used and y pounds of the $2.75 tea are used.
The first equation represents the total weight of the mixture: x + y = 80 (equation 1).
The second equation represents the average price per pound of the mixture: (3x + 2.75y) / 80 = 2.90 (equation 2).
To solve this system of equations, we can use the method of substitution or elimination.
Using substitution, we can solve equation 1 for x: x = 80 - y. Substituting this into equation 2, we have (3(80 - y) + 2.75y) / 80 = 2.90.
Simplifying the equation, we get (240 - 3y + 2.75y) / 80 = 2.90.
Combining like terms, we have (240 - 0.25y) / 80 = 2.90.
Cross-multiplying, we get 240 - 0.25y = 2.90 * 80.
Simplifying further, we have 240 - 0.25y = 232.
Subtracting 240 from both sides, we get -0.25y = -8.
Dividing both sides by -0.25, we find y = 32.
Substituting this value of y into equation 1, we have x + 32 = 80.
Solving for x, we get x = 80 - 32 = 48.
Learn more about pound here : brainly.com/question/29181271
#SPJ11
The eccentricity of the conic section below is
A. Closer to 0 than 1
B. Closer to 1 then 0

Answers
The eccentricity of the conic section below is: A. closer to 0 than 1.
What is a conic section?In Euclidean geometry, a conic section can be defined as a curve that is generated as the intersection of the surface of a right circular cone with a plane.
In Mathematics, there are four (4) types of conic section and these include the following with their eccentricity:
Hyperbola: its eccentricity is greater than one (1).Parabola: its eccentricity is equal to one (1).Ellipse: its eccentricity is 0 < e < 1.Circle: its eccentricity is equal to zero (0).In this context, we can reasonably infer and logically deduce that the eccentricity of the conic section is closer to zero (0) than one (1) because it represents a circle.
Read more on conic section here: https://brainly.com/question/4017703
#SPJ1
calculate the value of the integral of the same function 1/ p x2 y 2 over the annulus with outer radius 1 and inner radius δ
Answers
The value of the integral is 2π(2√r + C), where r ranges from δ to 1. To calculate the value of the integral of the function 1/√(x² + y²) over the annulus with outer radius 1 and inner radius δ, we can use polar coordinates.
First, let's convert the function to polar coordinates. We have:
1/√(x² + y²) = 1/√(r²)
Next, let's express the annulus in terms of polar coordinates. The outer radius 1 corresponds to r = 1, and the inner radius δ corresponds to r = δ.
Now, we can set up the integral:
∫∫(1/√(r²)) r dr dθ
To integrate with respect to r, we treat θ as a constant and integrate (1/√(r²)) r dr. This simplifies to:
∫(r/√(r²)) dr = ∫(1/√r) dr
Evaluating this integral, we get:
2√r + C
Now, we can integrate with respect to θ. Since the annulus spans a full circle, the limits of integration for θ are 0 to 2π.
∫(2√r + C) dθ = 2π(2√r + C)
To know more about integral visit:
https://brainly.com/question/31433890
#SPJ11
Complete question:
Calculate the value of the integral of the same function 1/√x² + y² over the annulus with outer radius 1 and inner radius δ.
Hhighihuyiuhhihihuhihiihiihihhihihiihihihiihiihiihihihihihihihihihihihihiihihihihihihiihiihiihihihihihihihihiihihiihihhiihihihihihihihihihiihiihihiihhihihiihhihihihhihihihihihihihhihihihi
Answers
Use pumping Lemma to prove that the following languages are not regular [ 5 pts each]. 1. L
1
={0
n
1
n
2
n
∣n≥0,Σ={0,1,2}} 2. L
2
={ωωω∣ω∈{a,b}
∗
}
Answers
In all cases, we can find a pumped string \(xy^kz\) that does not belong to L₂, which contradicts the assumption that L₂ is regular. Therefore, L₂ is not regular.
To prove that the given languages L₁ and L₂ are not regular using the pumping lemma, we need to show that for any hypothetical regular language L.
There exists a pumping length p such that for any string s in L of length at least p, we can pump s in a way that the pumped string is not in L.
1. L₁ = {\(0^n1^n2^n\) | n ≥ 0, Σ = {0, 1, 2}}
Assume L₁ is regular and let p be the pumping length. Consider the string s = \(0^p1^p2^p\). This string is in L₁ because it has the form \(0^n1^n2^n\), where n = p.
By the pumping lemma, we can decompose s into three parts: s = xyz, such that:
1. |y| > 0
2. |xy| ≤ p
3. For all k ≥ 0, \(xy^kz\) is in L₁.
Let's consider different cases for the possible placement of y in s.
y contains only 0s (\(y = 0^m\), where 1 ≤ m ≤ p).
In this case, when we pump y (k > 1), the number of 0s will exceed the number of 1s and 2s, and hence the pumped string \(xy^kz\) will not be in L₁.
y contains both 0s and 1s (\(y = 0^m1^k\), where 1 ≤ m + k ≤ p).
In this case, when we pump y (k > 1), the number of 0s and 1s will not be balanced with the number of 2s, and hence the pumped string \(xy^kz\) will not be in L₁.
y contains only 1s (\(y = 1^k\), where 1 ≤ k ≤ p).
In this case, when we pump y (k > 1), the number of 1s will exceed the number of 0s and 2s, and hence the pumped string \(xy^kz\) will not be in L₁.
y contains both 1s and 2s (\(y = 1^m2^k\), where 1 ≤ m + k ≤ p).
In this case, when we pump y (k > 1), the number of 1s and 2s will not be balanced with the number of 0s, and hence the pumped string \(xy^kz\) will not be in L₁.
Thus, in all cases, we can find a pumped string \(xy^kz\) that does not belong to L₁, which contradicts the assumption that L₁ is regular. Therefore, L₁ is not regular.
2. L₂ = {ωωω | ω ∈ {a, b}*}
Assume L₂ is regular and let p be the pumping length. Consider the string \(s = a^pb^pa^pb^pa^pb\). This string is in L₂ because it has the form ωωω, where ω = \(a^pb^p\).
By the pumping lemma, we can decompose s into three parts: s = xyz, such that:
1. |y| > 0
2. |xy| ≤ p
3. For all k ≥ 0, \(xy^kz\) is in L₂.
Let's consider different cases for the possible placement of y in s.
y contains only a's (\(y = a^m\), where 1 ≤ m ≤ p).
In this case, when we pump
y (k > 1), the number of a's will exceed the number of b's in the first or second occurrence of ω, and hence the pumped string \(xy^kz\) will not be in L₂.
y contains only b's (\(y = b^m\), where 1 ≤ m ≤ p).
In this case, when we pump y (k > 1), the number of b's will exceed the number of a's in the second or third occurrence of ω, and hence the pumped string \(xy^kz\) will not be in L₂.
y contains both a's and b's (\(y = a^mb^n\), where 1 ≤ m + n ≤ p).
In this case, when we pump y (k > 1), the number of a's or b's will exceed the number of the corresponding symbol in the corresponding occurrence of ω, and hence the pumped string \(xy^kz\) will not be in L₂.
Thus, in all cases, we can find a pumped string \(xy^kz\) that does not belong to L₂, which contradicts the assumption that L₂ is regular. Therefore, L₂ is not regular.
To know more about pumped string refer here:
https://brainly.com/question/30819932
#SPJ11
Complete Question
Use the pumping lemma to prove that the following languages are not regular:
L1 = {0^n 1^n 2^n | n ≥ 0, Σ = {0, 1, 2}}
L2 = {ωωω | ω ∈ {a, b}*}
For each language, apply the pumping lemma to show that there exists a pumping length (p) such that no matter how the string is divided into segments, it is not possible to pump the segments to generate all the strings in the language. This demonstrates that the languages are not regular.
a quasi-experimental design attempts to
Answers
The correct option A. quasi-experimental design; used to show that the independent variable's effect can be reversed.
Explain the quasi-experimental design?In that an independent variable is manipulated, quasi-experimental research is comparable to experimental research.
Similar to real trials, the quasi-experimental research approach seeks to establish the causal link between a variables under study. A quasi-experimental design, like a true experiment, seeks to establish a cause-and-effect link here between independent and dependent variable. However, unlike actual experiments, quasi-experimental studies use non-random criteria when assigning individuals to groups. A quasi-experiment, however, does not rely upon random assignment, unlike an actual experiment. Instead, non-random criteria are used to classify participants into groups.Thus, quasi-experimental design used to show that the independent variable's effect can be reversed.
To know more about the quasi-experimental design, here
https://brainly.com/question/14134556
#SPJ4
The correct question is-
One method used to demonstrate the reversibility of the effect of the independent variable is a(n):
A. quasi-experimental design.
B. interrupted time series design.
C. control series design.
D. ABA design.
Rewrite using a single positive exponent..-
7^2
——
7^-4
Answers
Answer:
7 ^2 ⋅ 7 ^4 = 49^6
Step-by-step explanation:
7² / 7 ⁻⁴
= 7²⁻⁽⁻⁴⁾
= 7 ⁽²⁺⁴⁾
= 7⁶
= 117649
Remember :-
xᵃ / xᵇ = xᵃ⁻ᵇ
___
Hope it helps ⚜
⁽
Raj went to the theatre to watch a traditional Indian dance performance with his family. The theatre had 1050 seats. There were 50% fewer $50-seats than $30-seats. 90% of the $30-seats and some $50-seats were sold. A total of $34 650 was collected. How many seats were unsold?
Answers
Total number of seats that remain unsold are 168.
What is statistics?
The branch of mathematics dealing with data collection, organization, analysis, interpretation and presentation.
Let's start by defining some variables to represent the unknowns in the problem:
Let x be the number of $30-seats.Let y be the number of $50-seats.From the problem, we know that:
The total number of seats is 1050: x + y = 1050.There were 50% fewer $50-seats than $30-seats: y = 0.5x.90% of the $30-seats and some $50-seats were sold, which means that the revenue from the $30-seats is 0.9(30x) = 27x, and the revenue from the $50-seats is 0.9(50y) = 45y.We also know that the total revenue collected is $34,650:
27x + 45y = 34650
Now we can substitute y = 0.5x from the second equation into the third equation and simplify:
27x + 45(0.5x) = 34650
27x + 22.5x = 34650
49.5x = 34650
x = 700
So there were 700 $30-seats and 350 $50-seats.
The number of sold $30-seats is 0.9(30x) = 567, and the number of sold $50-seats is 0.9(50y) = 315.
Therefore, the total number of seats sold is 882, and the number of unsold seats is:
1050 - 882 = 168
Learn more about statistics on:
https://brainly.com/question/15525560
#SPJ1
HELP PLEASE !!!! SHOW WORK TO ANSWER PLEASE

Answers
Answer: ~14°, ~62°
Step-by-step explanation:
See image. You should be able to easily calculate the last two angles.

A girl has 15 stacks of dimes, there were half as many pennies, so she had how many pennies. How many pennies did the girl have? Please give me an explanation of how you solved the math problem.
Answers
The girl had (15x) / 2 pennies, where "x" represents the number of dimes in a single stack.
We have,
The girl has 15 stacks of dimes.
There were half as many pennies.
To find the number of pennies, we can start by determining the number of dimes.
Since there are 15 stacks of dimes, we know that there are 15 times the number of dimes in a single stack.
Next,
We are told that there were half as many pennies as there were dimes.
So, to find the number of pennies, we need to divide the number of dimes by 2.
Let's say the number of dimes in a single stack is "x."
Then, the total number of dimes is 15x.
And since there are half as many pennies, the number of pennies would be (15x) / 2.
Thus,
The girl had (15x) / 2 pennies, where "x" represents the number of dimes in a single stack.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
I can solve rational equations using algebraic reasoning.
a. Looking at the equation below, for what
values of x can there NOT be
solutions? Explain your answer
(x+2/x+1)+(3x+15/2x+7)=3
b. Kristian started solving this problem
but got stuck.
(x+1)•((x+2/x+1)+(3x+15/2x+7))=(3)•(x+1)
x+2+((x+1)(3x+15)/(2x+7))=3x+3
What has Kristian done correctly so far? What
does Kristian need to do next?
c.
Finish the problem for Kristian. Show
all work.
Answers
For given linear equations, a. x cannot equal -1 or -3, c. x = -2 + 2 √(2) and x = -2 - 2√(2).
What is a linear equation ?
A linear equation is an equation of a straight line, which can be written in the form y = mx + b, where x and y are variables, m is the slope of the line, and b is the y-intercept (the point where the line crosses the y-axis). Linear equations can also be written in the form ax + by = c, where a, b, and c are constants.
Now,
a. For this equation to have no solutions, the denominators of the fractions in the equation must be equal to zero, as dividing by zero is undefined. Therefore, x cannot equal -1 or -3. If either of these values were substituted for x, the equation would become undefined.
b. Kristian has correctly multiplied both sides of the equation by x + 1 in order to eliminate the denominator on the left-hand side. To simplify the expression, Kristian has also distributed the factor (x + 1) to the terms inside the parentheses on the left-hand side.
c. Continuing from Kristian's work, we have:
x + 2 + (3x + 15)/(2x + 7) = 3x + 3
Multiplying both sides by the denominator 2x + 7 to eliminate the fraction, we get:
(2x + 7)(x + 2) + 3x + 15 = 3x + 3(2x + 7)
Expanding the parentheses and simplifying, we get:
2x² + 11x + 14 + 3x + 15 = 6x + 21
2x² + 14x - 6x + 29 = 6x + 21
2x² + 8x - 8 = 0
Dividing both sides by 2, we get:
x² + 4x - 4 = 0
Using the quadratic formula, we get:
x = (-4 ± √(16 + 16)) / 2
x = -2 ± 2√(2)
Therefore,
the solutions to the original equation are x = -2 + 2√(2) and x = -2 - 2√(2).
To know more about linear equations visit the link
brainly.com/question/29739212
#SPJ1
Please answer quickly

Answers
Answer:
\(y+2=\frac{5}{2} (x-6)\)
Step-by-step explanation:
point-slope form: y-y1=m(x-x1)
x1=6
y1=-2
m=5/2
\(y+2=\frac{5}{2} (x-6)\)
A street light is at the top of a 15 ft tall pole. A woman 6 ft tall walks away from the pole with a speed of 6 ft/sec along a straight path. How fast is the length of her shadow increasing when she is 50 ft from the base of the pole
Answers
Answer:
4 ft/sec
Step-by-step explanation:
Hope it helps
can someone pls help

Answers
The required area of the parallelogram and pentagon is 91 unit² and 75 unit².
What is surface area?The surface area of any shape is the area of the shape that is faced or the Surface area is the amount of area covering the exterior of a 3D shape.
A parallelogram in is shown in figure 1 with the dimensions height = 7 and base = 13,
Area of the parallelogram = 13 × 7 = 91 unit²
Now,
A pentagon is shown in figure 2,
Area of the pentagon = 5 [1/2 × height × side]
= 5 [1/2 × 5 × 6]
= 75 suqare units.
Thus, the required area of the parallelogram and pentagon is 91 unit² and 75 unit².
Learn more about the surface area here: https://brainly.com/question/2835293
#SPJ1
Question 4(Multiple Choice Worth 2 points)
(Systems of Linear Equations MC)
Which point is a solution of the system of linear equations?
x − 3y = −2
y = −3x + 4
A. (1, 1)
B. (1, −1)
C. (−1, 1)
D. (−1, −1)
Answers
A point which is a solution of the system of linear equations include the following: A. (1, 1).
How to graph the solution to this system of equations?In order to to graph the solution to the given system of equations on a coordinate plane, we would use an online graphing calculator to plot the given system of equations and then take note of the point of intersection;
x − 3y = −2 ......equation 1.
y = −3x + 4 ......equation 2.
Next, we would use an online graphing calculator to plot the given system of equations as shown in the graph attached below.
Based on the graph (see attachment), we can logically deduce that the solution to the given system of equations is the point of intersection of the lines on the graph representing each of them, which lies in Quadrant I and it is given by the ordered pair (1, 1).
Read more on equation here: brainly.com/question/4110837
#SPJ1
