Find the greatest common factor of 54gh, 72g
Answers
The greatest common factor the expressions is 2g
Finding the greatest common factor the expressionsFrom the question, we have the following parameters that can be used in our computation:
54gh, 72g
The terms of the above expressions are
54gh and 72g
The terms of the above expressions have common factors g and 2
So, we have
2g is common in 54gh and 72g
Hence, the greatest common factor the expressions is 2g
Read more about GCF at
https://brainly.com/question/17067741
#SPJ1
Related Questions
classify the triangle according to its SIDES and ANGLES.

Answers
Answer:
this is a right angled triangle
Step-by-step explanation:
It has a 90 degree angle
the hypotenuse is the longest
The other two sides adjacent to the right angle are perpendicular
It could also be called an isosceles right angled triangle
Answer:
Right angled and Isosceles
Step-by-step explanation:
Right angled because one corner of the triangle is marked with a square, which shows it is 90degrees.
Isosceles because 2 angles and 2 sides have been marked with similar lines and curves, which shows that they are equal in length. When 2 angles and 2 sides are equal, the triangle is isosceles.
Hope this helps.
Good Luck
A magazine provided results from a poll of adults who were asked to identify their favorite pie. Among the ​respondents, ​% chose chocolate​ pie, and the margin of error was given as percentage points. Describe what is meant by the statement that​ "the margin of error was given as percentage​ points."
Answers
The statement indicates that the interval 12%±5% is likely to contain the true population percentage of people that prefer chocolate pie.
According to the statement
we have a given that the Among the 1000 respondents,
12% chose chocolate pie, and the margin of error was given as
±5 percentage points.
and we have to explain the statement that the margin of error was given as ±5 percentage points.
We know that the interval is a set of real numbers that contains all real numbers lying between any two numbers of the set.
And this statements also indicates the interval between the like and unlike respondents of chocolate pie.
So, this statement indicates that the interval 12%±5% is likely to contain the true population percentage of people that prefer chocolate pie.
So, The statement indicates that the interval 12%±5% is likely to contain the true population percentage of people that prefer chocolate pie.
Learn more about Interval here https://brainly.com/question/1600302
#SPJ4
james and mark are delivering newspapers. if james delivers 130 papers in one hour and Mark delivers 210 papers in three hours,how long will it takes both of them working together to deliver 1000 newspapers?
Answers
Answer:
James deliver newspaper in 1 hour=130
Marks deliver newspaper in 1 hour= 210/3=70
so lf they work together to deliver 1000 newspaper they take 130+70=200. 1000/200=5.
so they take 5 hours to deliver 1000 newspaper.
It would take 5 hours for James and Mark to deliver 1000 newspapers.
EquationEquation is an expression used to show the relationship between two or more variables and numbers.
James delivers 130 papers in one hour (130/1) and Mark delivers 210 papers in three hours(70 papers in 1 hours), hence:
For 1000 newspapers:
(130 + 70)t = 1000
t = 5 hours
It would take 5 hours for James and Mark to deliver 1000 newspapers.
Find out more on equation at: https://brainly.com/question/14323743
PU
Decinal
Rounding
Round 2,384.653
to the nearest whole number.
Answers
Answer:
Given value = 2384.653
We are required to round off to the nearest whole number.
Step-by-step explanation:
To round the digit or number nearest whole number first see the digit or number at the first decimal place and tenth place value. If the value at the tenth place is 5 or more than 5 then the one place number will be increased by one. For example. 9.63 will be written as the 10 because after decimal the value is more than 5.
Similarly, the 2384.653 is written as 2385.
Petra claims that he can use the Associative Property of Multiplication to rewrite (9.5 x 9) + 1 as 9.5 X 10. Is Petra correct? Explain.
Answers
(9.5 x 9) + 1 = 86.5
9.5 x 10 = 95
Answer:
No
Step-by-step explanation:
If he used that method it would end up as 95
in the original equation the answer is 86.5
I need help on this, please help

Answers
Answer:i tihnk football is .45 and tennis is .18?
Step-by-step explanation:
i dont know if this is right but im pretty sure it is
find the area of the region enclosed by one loop of the curve. r = sin(6θ)
Answers
Area of the region enclosed by one loop of the curve is pi/288.
To find the area of the region enclosed by one loop of the curve, we can use the formula for the area of a polar region:
A = 1/2 * ∫(r^2)dθ
We can use this formula with the equation for r given:
A = 1/2 * ∫(sin^2(6θ))dθ
This integral can be simplified by noting that sin^2(x) = (1/2)(1 - cos(2x))
Thus,
A = 1/2 * ∫(1/2)(1 - cos(12θ))dθ
This integral can be solved by noting that the antiderivative of (1/2)(1 - cos(12θ)) is (1/24)(sin(12θ) + θ).
Therefore, the area enclosed by one loop of the curve is
A = 1/2 * ((1/24)(sin(12θ) + θ)) evaluated from 0 to pi/6
A = (1/48)(sin(2pi) + pi/6)
= (1/48)(0 + pi/6)
= pi/288
To know more about area of loop of the curve refer to:
brainly.com/question/30114510
#SPJ4
Erika draws a hexagon. Maria draws a pentagon. Who draws the shape with more sides? How many more sides does that shape have?
Answers
hexagon has 6 sides, and a pentagon has 5, can I have a crown?
Answer:
Erika
one more side
Step-by-step explanation:
Pentagon has 5 sides
Hexagon has 6 sides
PLEASE HELP FREE 15 POINTS
A television screen measures approximately 15.5 in. high and 19.5 in. wide.
Screens are measured and advertised by the length of the diagonal of its screen.
What measurement to the nearest hundredth should be used to advertise this
television
Answers
Answer:
19.5 because if we do hundred then it well equal to 19.5
The congruent sides of an isosceles triangle are each 50
centimeters. The vertex angle measures 40°. What is the
length of the base of the triangle? Round to one decimal
place.
Select one:
O 34.2 cm
17.1 cm
28.3 cm
20.6 cm
Answers
The length of the base of the triangle is approximately 34.2 cm.
To find the length of the base of the isosceles triangle, we can use the cosine rule.
The cosine rule states that in a triangle with sides of lengths a, b, and c, and the angle opposite to side c is A, we have:
c² = a² + b² - 2ab × cos(A)
In this case, the congruent sides of the isosceles triangle are each 50 centimeters, so we have:
a = b = 50 cm
The vertex angle measures 40°, so A = 40°. Let's calculate the length of the base (c):
c² = 50² + 50² - 2 × 50 × 50 × cos(40°)
Now we can solve for c:
c² = 2500 + 2500 - 5000 × cos(40°)
c² = 5000 - 5000 × cos(40°)
c² = 5000 × (1 - cos(40°))
c = sqrt(5000 × (1 - cos(40°)))
Using a calculator, we find that c ≈ 34.2 cm.
Therefore, the length of the base of the triangle is approximately 34.2 cm.
So, the correct answer is: 34.2 cm
Learn more about cosine rule click;
https://brainly.com/question/28716982
#SPJ1
The height of a house is 52 ft. A tree beside the house is 7.5 ft more than twice as tall. What is the height, in feet, of the tree? HELP ME THEN ILL HELP U
Answers
The height in feet of the tree is 111.5 ft.
How to find the height of a tree?The height of a house is 52 ft.
A tree beside the house is 7.5 ft more than twice as tall.
The height of the tree is as follows:
let
x = height of the house
Therefore,
The height of the house = x = 52 ft
Hence,
height of the tree = 7.5 + 2x
height of the tree = 7.5 + 2(52)
height of the tree = 7.5 + 104
height of the tree = 111.5
height of the tree = 111.5 ft
learn more on height here: https://brainly.com/question/13868851
#SPJ1
determine the solutions of the equation: absolute value of the quantity one fifth times x plus 2 end quantity minus 6 equals two.
Answers
Answer: The solutions of the absolute value equation are given by:
x = -41 and x = 49.
What is the absolute value function?
The absolute value function is defined by:
|x| = x, x >= 0.
|x| = -x, x < 0.
The absolute value function measures the distance of a point x to the origin, that is, the distance to x = 0. From this, we get that |x| = a can mean either that:
x = a, or;
x = -a.
In this problem, the equation is given by:
Hence:
0.2|x - 4| = 9
|x - 4| = 45
The first possible solution is:
x - 4 = 45
x = 49.
The second possible solution is:
-x + 4 = 45
-x = 41
x = -41.
Hence the solutions are x = -41 and x = 49.
More can be learned about the absolute value function at brainly.com/question/24734454
Step-by-step explanation:
Please help me now :c
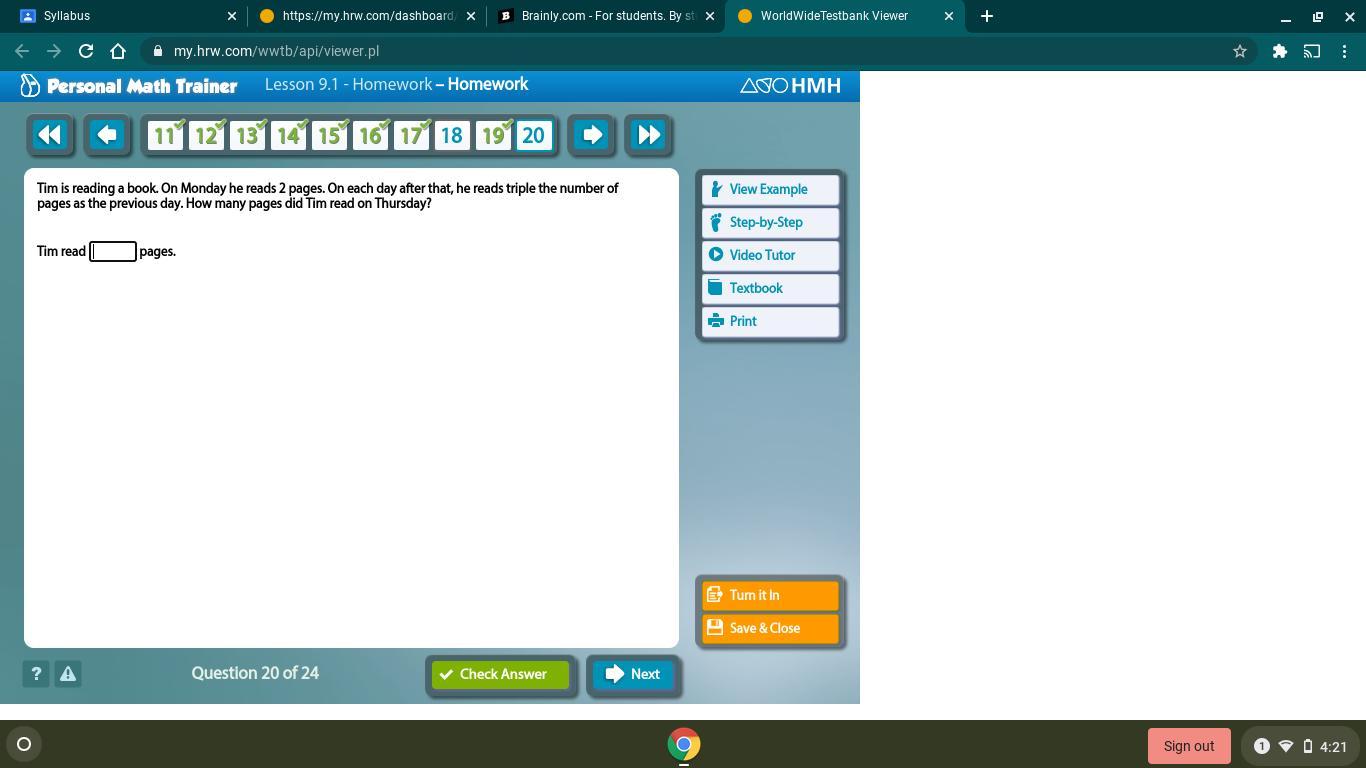
Answers
On Monday he reads 2 pages, on Tuesday he reads 6 pages (triple of 2: 2 + 2 + 2 = 6), on Wednesday he reads 18 pages (triple of 6: 6 + 6+ 6 = 18), on Thursday he reads 54 pages (triple of 18: 18 + 18 + 18 = 54).
HELP!!!
Which situation is unlikely?
Flipping a coin and it landing on heads
Spinning a spinner labeled 1-4 and landing on a number greater than 1
Rolling a number cube labeled 1-6 and getting a 1 or 2
Answers
Answer: I would say rolling a number cube
Step-by-step explanation:
when flipping a coin you will have a 1/2 chance of landing on heads and then when spinning the spinner you would have a 3/4 chance since there is 3 numbers greater then 1 and then with the cube since it has 6 sides and your only getting 1 or two you would have a 2/6 chance.
can someone pls help me asap i need to turn this in in 4 minutes please

Answers
Answer: A is 80 and B is 85 train B is going faster
Step-by-step explanation:
hope this helps
because A is already given and to find b divide d/t to find constant and after doing so b is 5km per hour faster
Find the slope of the points (-10, -52)
and (-70, -32)
Answers
Answer:
Slope= -1/3
Step-by-step explanation:
The slope is found using (y₂ - y₁) / (x₂ - x₁)
(y₂ - y₁)
So let's do the numerator first with the y. -52-(-32). The two negative signs make 32 positive so -52 + 32= -20
(x₂ - x₁)
Now the denominator, x. -10-(-70). Same thing here, the two negative signs make 70 positive so -10 + 70 = 60
(y₂ - y₁) / (x₂ - x₁)
Now put them together so -20/60 which equals -1/3 which the slope
By the argument in the last video, if the Xi are i.i.d. with mean μ and variance σ2 , and if Mn=(X1+⋯+Xn)/n , then we have an inequality of the form
P(|Mn−μ|≥ϵ)≤aσ2n,
for a suitable value of a .
a) If ϵ=0.1 , then the value of a is:
unanswered
b) If we change ϵ=0.1 to ϵ=0.1/k , for k≥1 (i.e., if we are interested in k times higher accuracy), how should we change n so that the value of the upper bound does not change from the value calculated in part (a)?
Answers
The value of the constant "a" in the inequality P(|Mn - μ| ≥ ε) ≤ aσ^2/n is 1.
The value of "n" can remain the same when changing ε from 0.1 to 0.1/k, as long as the desired upper bound remains unchanged.
To determine the value of the constant "a" in the inequality P(|Mn - μ| ≥ ε) ≤ aσ^2/n, we can use Chebyshev's inequality. Chebyshev's inequality states that for any random variable with mean μ and variance σ^2, the probability that the random variable deviates from its mean by at least k standard deviations is at most 1/k^2.
In our case, we have ε = 0.1 and we want to find the value of "a" for this specific value. Since ε is the desired accuracy, we are interested in the probability of the sample mean Mn deviating from the true mean μ by at least ε. Using Chebyshev's inequality, we have:
P(|Mn - μ| ≥ ε) ≤ 1/k^2
We can rewrite this inequality as:
P(|Mn - μ| ≥ 0.1) ≤ 1
Therefore, the value of "a" for ε = 0.1 is 1.
For the second part of the question, where ε = 0.1/k, we want to determine how to change the value of "n" so that the upper bound remains the same. Substituting ε = 0.1/k into the inequality, we have:
P(|Mn - μ| ≥ 0.1/k) ≤ 1
To keep the upper bound unchanged, we need to ensure that the right-hand side of the inequality remains 1. Since the right-hand side does not depend on "n", changing ε to 0.1/k does not require any adjustment in the value of "n".
To learn more about inequalities visit : https://brainly.com/question/25275758
#SPJ11
4. Write the indicated proof. Given: AABC = AADC Prove: AC bisects /BAD and AC bisects /BCD

Answers
The segment AC is the angle bisector of angle BAD and angle BCD.
What is an angle bisector?A ray, segment, or line that divides a given angle into two equal angles is known as an angle bisector.
When something is bisected or bisected, it is split into two equal sections. In geometry, an angle bisector is a line or ray that divides a triangle into two equal angles.
Given that ΔABC ≅ ΔADC Prove: AC bisects ∠BAD and AC bisects ∠BCD.
From the given data it is concluded that all the corresponding angles of the triangle are equal to each other.
In the triangle ABC and ADC:-
∠BAC = ∠DAC
∠BCA = ∠DCA
From the above proof, it is concluded that the AC bisects ∠BAD and ∠BCD.
Therefore, the segment AC is the angle bisector of angle BAD and angle BCD.
To know more about an angle bisector follow
https://brainly.com/question/24677341
#SPJ1
Find the vectors
u + v,
u − v,
3u −1/2v
u = (2, −6, 3)
v = (0, 4, −1)
(Simplify your answers completely.)
Answers
Answer:
(u+v) =(2 , -2, 2)
(u-v) =(2, -10,4)
3u-1/2v=(6, -20, 7.5)
Step-by-step explanation:
ask for explanation if answers are right
The vectors are:
u + v = (2, -2, 2)
u - v = (2, -10, 4)
3u - (1/2)v = (6, -20, 19/2)
Given:
u = (2, -6, 3)
v = (0, 4, -1)
u + v:To find u + v, we add the corresponding components of u and v.
u + v = (2, -6, 3) + (0, 4, -1) = (2+0, -6+4, 3-1) = (2, -2, 2)
u - v:To find u - v, we subtract the corresponding components of v from u.
u - v = (2, -6, 3) - (0, 4, -1) = (2-0, -6-4, 3-(-1)) = (2, -10, 4)
3u - (1/2)vTo find 3u - (1/2)v, we multiply u by 3 and v by (1/2), and then subtract the corresponding components.
3u - (1/2)v = 3(2, -6, 3) - (1/2)(0, 4, -1) = (6, -18, 9) - (0, 2, -1) = (6-0, -18-(1/2)4, 9+(1/2)) = (6, -18-2, 9+1/2) = (6, -20, 19/2)
Therefore, the vectors are:
u + v = (2, -2, 2)
u - v = (2, -10, 4)
3u - (1/2)v = (6, -20, 19/2)
Read more on Vectors here: https://brainly.com/question/25705666
#SPJ11
What is the pattern as the exponents decrease?
subtract 5 from the previous value
subtract 100 from the previous value
divide the previous value by 5
divide the previous value by 25
Answers
Answer:
divide the previous value by 5
Step-by-step explanation:
5^2=25, 5^1=5, 25/5=5
The answer is C :)
Have a nice day
Correct on edge.
A study was conducted to compare the proportion of drivers in boston and new york who wore seat belts while driving. Data were collected, and the proportion wearing seat belts in boston was 0. 581 and the proportion wearing seat belts in new york was 0. 832.
Answers
z = -2.51 is the required test statistic.
What is the test statistic?A statistic employed in statistical hypothesis testing is known as a test statistic.
A test statistic, which can be thought of as a numerical summary of a data set that condenses the data into a single value that can be used to conduct the hypothesis test, is how a hypothesis test is commonly expressed.
The probability value, or p-value, indicates the likelihood that your data could have been true under the null hypothesis.
This is accomplished by estimating the probability of your test statistic, which is the figure obtained from a statistical analysis of your data.
So, we have to use: Ha: pB < pNY
This implies that the alternative thesis is revised as follows:
Ha: pB - pNY < 0
In contrast to the null hypothesis:
H₀: pB - pNY = 0
This is the test statistic:
z = X - μ/a
Now, pB = 0.581, pNY = 0.832.
It follows that: X = 0.581 - 0.832 = -0.251
The test for the null hypothesis is 0.
This follows to: μ = 0
Standard deviation: 0.1
This follows to: s = 0.1
Test statistic:
z = X - μ/a
z = -0.251-0/0.1
z = -2.51
Therefore, z = -2.51 is the required test statistic.
Know more about the test statistic here:
https://brainly.com/question/15110538
#SPJ4
Complete question:
A study was conducted to compare the proportion of drivers in Boston and New York who wore seat belts while driving. Data were collected, and the proportion wearing seat belts in Boston was 0.581 and the proportion wearing seat belts in New York was 0.832. Due to local laws at the time the study was conducted, it was suspected that a smaller proportion of drivers wear seat belts in Boston than New York.
Find the test statistic for this test using Ha: pB < pNY. (Use standard error = 0.1.)
Mike is hiking on a mountain and stops 105.3 feet above sea level. The base of the mountain is 3.8 feet below sea level. What is the vertical distance between Mike and the base of the mountain?
Answers
Mike comes to a stop 105.3 feet above sea level while trekking on a mountain. The vertical separation between Mike and the mountain's base is 101.5 feet .
Given that,
Mike comes to a stop 105.3 feet above sea level while trekking on a mountain. There are 3.8 feet of sea level below the mountain's base.
We have to find what is the vertical separation between Mike and the mountain's base.
The Mike comes to a stop 105.3 feet above sea level while trekking on a mountain.
3.8 feet of sea level below the mountain's base.
We just have to do the difference of the above sea level feet and below sea level feet.
=105.3-3.8
=101.5
Therefore, the vertical separation between Mike and the mountain's base is 101.5 feet .
To learn more about feet visit: https://brainly.com/question/15658113
#SPJ1
Feng has 54 m of fencing to build a four-sided fence around a rectangular plot of land. The area of the land is 180 square meters. Solve for the dimensions (length and width) of the field.
Answers
The dimensions of the field are: 87.95 m and 2.05 m
How to maximize the dimensions?Let the length of the plot be x and breadth y. Then, its perimeter is:
p = 2(x + y)
p = 180
From this, we can express y in terms of x:
2(x + y) = 180
x + y = 90
y = 90 − x
The area of the plot is:
A = xy
A = x(90 − x)
A = −x² + 90x
We need this expression to be equal to 180 to find the borders of the interval we need:
−x² + 90x = 180
x² - 90x + 180 = 0
x = 87.95 m and 2.05 m
Read more about Maximizing Area at: https://brainly.com/question/14903714
#SPJ1
Answer: 15 meters by 12 meters
Step-by-step explanation:
the first explanation is incorrect, i used it and its wrong
Find the absolute maximum and absolute minimum values of the function
f(x)= x3 + 6x2 −63x +8
over each of the indicated intervals.
(a) Interval = [−8,0].
Answers
The absolute minimum value of the function is 120 which occurs at x = -8. To find the absolute maximum and minimum values of the function f(x) = x^3 + 6x^2 - 63x + 8 over the interval [-8, 0], you need to first find the critical points by taking the first derivative and setting it to zero, and then evaluate the function at the critical points and the endpoints of the interval.
1. Take the derivative of f(x):
f'(x) = 3x^2 + 12x - 63
2. Set f'(x) to zero and solve for x:
3x^2 + 12x - 63 = 0
Divide by 3:
x^2 + 4x - 21 = 0
Factor:
(x+7)(x-3) = 0
So, the critical points are x = -7 and x = 3.
However, only x = -7 is within the interval [-8, 0].
3. Evaluate f(x) at the critical point x = -7 and at the endpoints of the interval, x = -8 and x = 0:
f(-7) = (-7)^3 + 6(-7)^2 - 63(-7) + 8 = 120
f(-8) = (-8)^3 + 6(-8)^2 - 63(-8) + 8 = 64
f(0) = 0^3 + 6(0)^2 - 63(0) + 8 = 8
Comparing the values of f(x) at these points, we find:
Absolute maximum: f(-7) = 120
Absolute minimum: f(0) = 8
Learn more about minimum here:
https://brainly.com/question/21426575
#SPJ11
Please helppp meeeeeeeeeeeeeeeseseeedeeeeeee

Answers
Answer:
The solution x > 10 can be represented in two ways such as:
Interval Notation: (10, ∞)Inequality Notation: x > 10Step-by-step explanation:
Let 'x' be the solution to the inequality
From the given line, it is clear that
x > 10
It means the value of x is greater than 10, which means the solution contains all the positive real numbers greater than 10.
From the number line, it is clear that the number line would include all the numbers on the right-hand side of the 10 number.
The number 10 is not included; thus the number line indicates an open circle on 10, meaning 10 is not include in the solution.
Thus, the solution x > 10 can be represented in two ways such as:
Interval Notation: (10, ∞)Inequality Notation: x > 10Solve for x in simplest form 3 = 5/2 (3x - 2)
Answers
The answer is 16/15, don’t ask ok, used a calculator
The solution is here:

donald needs to stamp 145 pieces of mail. he has finished 97 pieces. how many more does he have to do?
Answers
To complete the mail, Donald needs to stamp 48 pieces of mail if the total mails are 145 and he has done 97 pieces.
To calculate the number of mail to be stamped, one has to subtract the already stamped mails from the total number of mails.
Total number of mails = 145 mails
Number of mails already stamped = 97 mails
Mails left to be stamped = total number of mails - mails that are already stamped
= 145 - 97
= 48 mails
Thus, Donald has to stamp 48 more mails in order to total mail of 145
Learn more about Subtraction:
https://brainly.com/question/25421984
#SPJ4
How do you solve equations that contain multiplication or division?
You apply the (select) v operation-(select)
(select) for division equations—to (select)
for multiplication equations and
of the equation.
Answers
Equations that contain multiplication or division, you should use the inverse operations of multiplication or division. The inverse operation is a mathematical operation that reverses the effect of another operation.
For multiplication equations, the inverse operation is division, and for division equations, the inverse operation is multiplication. Let's see how to apply these inverse operations to solve equations that contain multiplication or division.Division equations:To solve equations that contain division, you should use multiplication as the inverse operation. Follow these steps:1. If there is a term added to or subtracted from the variable, move it to the opposite side of the equation.2. Multiply both sides of the equation by the divisor of the variable.3.
Simplify the equation and solve for the variable.Example: Solve the following equation for x: 4x ÷ 2 = 10Solution:1. Move the term added to or subtracted from the variable to the opposite side of the equation. 4x ÷ 2 = 10 4x = 2 × 10 4x = 202. Multiply both sides of the equation by the divisor of the variable. 4x = 20 x = 20/4 x = 5
To know more about Equations visit:-
https://brainly.com/question/29538993
#SPJ11
f(x) = |x − 5| + 2 Which of the following statements about the y-values of the graph of the function is true?
Answers
The answer will be option B. The y-values are all greater than or equal to 2.
What is a function?A function in mathematics set up a relatioship between the dependent variable and independent variable. on changing the value of the independent variable the value of the dependent variable also changes.
Here no matter what x is, y will always be positive, because the absolute value of x-5 will always be positive. The smallest value that y can be is when x is 5, because then the absolute value of x-5 is 0, and then y is 2.
Therefore, the correct answer will be option B. The y-values are all greater than or equal to 2.
To know more about function follow
https://brainly.com/question/2833285
#SPJ1
Can someone explain and help me with this?

Answers
Answer:
A) a²-2a+2a-4 the a is correct check my explanation to understand the answer.
Step-by-step explanation:
(a+2)(a-2)= a²-2a+2a-4