Find the length of the arc.
120°
6ft
Answers
Answer:
The length of the arc is 8*pi cm. An arc that subtends a central angle of 120 degrees has a length of 120/360 = 1/3 the length of the total circumference of the circle. We know the entire circumference of the circle is 2πr, which in this case is 2π*12 = 24π.
Step-by-step explanation:
sorry I only have the 8
Related Questions
Three pizza are shared equally among 12 people.what fraction of a pizza will each person get?
A
4/1
B
3/1

Answers
Answer:
d) 1/12
Step-by-step explanation:
Need help with this one

Answers
Answer: \(\frac{9g}{4y}\)
Step-by-step explanation:
\(\frac{6g}{2} \times \frac{3}{4y}=\frac{18g}{8y}=\frac{9g}{4y}\)
what are the solutions of the system of equations y=-(x+2)^2+1 and y=2x+5?
A) (-4,-3) and (-2,1)
B) (-4,-3) and (2,1)
C) (-4,5) and (2,1)
D) (-4,5) and (-2,1)
Answers
The solutions of the system of equations are (-2, 1) and (-4, 5). The answer is D) (-4,5) and (-2,1).
What is equation ?
In mathematics, an equation is a statement that two expressions are equal. It typically contains one or more variables, which are unknowns that can take on different values. An equation is written using an equal sign (=) to indicate that the expressions on either side have the same value.
To solve the system of equations y = -\((x+2) ^{2}\) + 1 and y = 2x + 5, we can set the two expressions for y equal to each other and solve for x:
-\((x+2) ^{2}\) + 1 = 2x + 5
Expanding the left side and simplifying, we get:
-x*x - 4x - 4 + 1 = 2x + 5
-x*x - 6x - 8 = 0
Dividing both sides by -1, we get:
x*x+ 6x + 8 = 0
Factoring the left side, we get:
(x+2)(x+4) = 0
So the solutions for x are x = -2 and x = -4.
To find the corresponding y-values for each solution, we can plug in each value of x into either equation and solve for y. Let's use the equation y = -\((x+2) ^{2}\)+ 1:
When x = -2, y = -\((x+2) ^{2}\) + 1 = -(0) + 1 = 1.
When x = -4, y =-\((x+2) ^{2}\)+ 1 = -(-4) + 1 = 5.
Therefore, the solutions of the system of equations are (-2, 1) and (-4, 5).
The answer is D) (-4,5) and (-2,1).
To learn more about Equation from given link.
https://brainly.com/question/30732180
#SPJ1
Answer:
A) (-4,-3) and (-2,1)
Step-by-step explanation:
If you graph the system on desmos and graph the points you will see that those are the points that give a solution to the system
Explain how to find the 41st term of the arithmetic sequence where a1=5 and a7=34.
Answers
Answer:
198 1/3
Step-by-step explanation:
arithmetic sequence formula for the nth term:
aₙ = a₁ + (n-1)d
d = the common difference between each term
a₇ = a₁ + (7-1)d
34 = 5 + 6d
subtract 5 from both sides to isolate d and its coefficient
29 = 6d
divide both sides by 6 to isolate d
d = 29/6
a₄₁ = a₁ + (n-1)d
= 5 + (41-1)d
= 5 + 40d
= 5 + 40(29/6)
= 198 1/3
The table shows how many children and adults prefer each of two different fruits. How would you find the joint relative frequency of being an adult who prefers watermelon?%0D%0A%0D%0AWatermelon%09Grapes%09Total%0D%0AChild%09132%0985%09217%0D%0AAdult%09111%09117%09228%0D%0ATotal%09243%09202%09445%0D%0A%0D%0AA.%0D%0ADivide 111 by 228.%0D%0A%0D%0AB.%0D%0ADivide 111 by 243.%0D%0A%0D%0AC.%0D%0ADivide 111 by 445.%0D%0A%0D%0AD.%0D%0ADivide 243 by 445.
Answers
The joint relative frequency is calculated by dividing the frequency of a specific subset (in this case, the number of adults who prefer watermelon) by the total number of data points.
Here, the specific subset is adults who prefer watermelon, which is 111. The total number of data points is the sum of all children and adults, regardless of fruit preference, which is 445.
So, to find the joint relative frequency of being an adult who prefers watermelon, you would divide 111 by 445.
Hence, the correct answer is:
C. Divide 111 by 445.
Cynthia orders 27 prints of a photograph she took . It costs her a total of $242.73 . How much does each print cost ?
Answers
Answer:
8.99
Step-by-step explanation:
Answer:
$8.99 for each print
Step-by-step explanation:
242.73 divided by 27 = 8.99
A florist wants to determine if a new additive would
Using this dotplot and the difference in proportions
help extend the life of cut flowers longer than the
from the samples, is there convincing evidence that
original additive. The florist randomly selects 20
the new additive was more effective?
carnations and randomly assigns 10 to the new
additive and 10 to the original additive. After three
O Yes, because a difference in proportions of 0.2 or
weeks, 5 carnations placed in the new additive still
more occurred 41 out of 200 times, meaning the
looked healthy, and 3 carnations placed in the original
difference is statistically significant and the new
additive still looked healthy. The difference in
additive is more effective.
proportions (new - original) for the carnations that still
Yes, because a difference in proportions of 0.2
or
looked healthy after three weeks was 0.2. Assuming
less occurred 159 out of 200 times, meaning the
there is no difference in the additives, 200 simulated
difference is statistically significant and the new
differences in sample proportions are displayed in the
additive is more effective
dotplot
© No, because a difference in proportions of 0.2 or
Simulation for Difference in
more occurred 41 out of 200 times, meaning the
Proportions of Carnation Health
difference is not statistically significant and the new
additive is not more effective
No. because a difference in proportions of 0.2 OI
less occurred 159 out of 200 times, meaning the
Mark this a
Save and Exit
Next
Submit
Answers
It was more effective because a difference in proportions of 0.2 looked healthy after three weeks was 0.2.
What is a dot plot?A dot plot is a graph that displays individual data points as dots (markers) on a number line, showing the distribution of a dataset. It is similar to a histogram but is used when the data set has many unique values or when the data is not continuous.
In this case, we are told that a florist wants to determine if a new additive would help extend the life of cut flowers longer than the from the sample.
Learn more about dot plot:https://brainly.com/question/22746300
#SPJ1
A paint machine dispenses dye into paint cans to create different shades of paint. The amount of dye dispensed into a can is known to have a normal distribution with a mean of 5 milliliters (ml) and a standard deviation of 0.4 ml. Answer the following questions based on this information. Find the dye amount that represents the 9th percentile of the distribution.
Answers
Answer:
4.464 ml
Step-by-step explanation:
Given that:
mean (μ) = 5 mm, standard deviation (σ) = 0.4 ml
The z score is a score in statistics used to determine by how many standard deviation the raw score is above or below the mean. If the z score is positive then the raw score is above the mean and if the z score is negative then the raw score is below the mean It is given by:
\(z=\frac{x-\mu}{\sigma}\)
From the normal distribution table, the 9th percentile (0.09) corresponds to a z score of -1.34
\(z=\frac{x-\mu}{\sigma}\\\\-1.34=\frac{x-5}{0.4}\\\\x-5=-0.536\\\\x=5-0.536\\\\x=4.464\)
The dye amount that represents the 9th percentile of the distribution is 4.464 ml
Which shows one way to determine the factors of x3 - 12x7 - 2x + 24 by grouping?
Answers
The factored form of the polynomial x^3 - 12x^2 - 2x + 24 by grouping is (x - 12)(x^2 - 2).
To determine the factors of the polynomial x^3 - 12x^2 - 2x + 24 by grouping, we can follow these steps:
Step 1: Group the terms in pairs. In this case, we can pair the first two terms and the last two terms:
(x^3 - 12x^2) + (-2x + 24)
Step 2: Factor out the greatest common factor from each pair. From the first pair, we can factor out x^2, and from the second pair, we can factor out -2:
x^2(x - 12) - 2(x - 12)
Step 3: Notice that we now have a common binomial factor of (x - 12) in both terms. Factor out this common binomial factor:
(x - 12)(x^2 - 2)
Therefore, the factored form of the polynomial x^3 - 12x^2 - 2x + 24 by grouping is (x - 12)(x^2 - 2).
To more on factors:
https://brainly.com/question/15824403
#SPJ8
Los organizadores de la Feria de Alimentos colocan un contenedor de agua que mide 2,76 metros de largo, por 23,5 decímetros de ancho y por 196 centímetros de alto. ¿Cuál es el volumen del contenedor? Expresa la respuesta en metros cúbicos con aproximación a centésimos.
Answers
The volume of the container is approximately 12.9516 cubic meters when rounded to the nearest hundredth.
To find the volume of the container, we need to multiply its length, width, and height. Let's convert the given measurements to meters to ensure consistent units.
The length of the container is 2.76 meters.
The width of the container is 23.5 decimeters, which is equal to 2.35 meters (since 1 decimeter = 0.1 meters).
The height of the container is 196 centimeters, which is equal to 1.96 meters (since 1 meter = 100 centimeters).
Now we can calculate the volume of the container:
Volume = Length × Width × Height
Volume = 2.76 meters × 2.35 meters × 1.96 meters
Volume ≈ 12.9516 cubic meters (rounded to four decimal places)
Therefore, the volume of the container is approximately 12.9516 cubic meters when rounded to the nearest hundredth.
for such more question on volume
https://brainly.com/question/6204273
#SPJ8
The distance from Will's house to a park is 1 9/10 miles. Will
leaves his house and walks 2/5 mile toward the park. About
how much farther does he have to walk to reach the park?
Answers
Answer:
\(\boxed{1\dfrac{1}{2}\;miles}\)
Step-by-step explanation:
Convert 1 9/10 to an improper fraction and then the calculation becomes simpler
\(1 \dfrac{9}{10 } = \dfrac{ 1 \cdot 10 + 9}{10} = \dfrac{19}{10}\\\\\)
Since Will has already walked 2/5 of a mile to the park, the remaining distance
\(= \dfrac{19}{10} - \dfrac{2}{5}\\\\\)
Make the denominators the same by multiplying both the numerator and denominator of 2. This does not change the original value of 2/5
\(\dfrac {2 \times 2}{5 \times 2} = \dfrac{4}{10}\\\\\)
Therefore the remaining distance is
\(\dfrac{19}{10} - \dfrac{2}{5}\\\\\\= \dfrac{19}{10} - \dfrac{4}{10}\)
Since the denominator is the same we can simply subtract the numerator terms and use 10 as the denominator for the result:
\(= \dfrac{19-4}{10} = \dfrac{15}{10} \\\\\)
Dividing numerator and denominator by 5 reduces it to the lowest fraction
\(\dfrac{15 \div 5}{10 \div 5} = \dfrac{3}{2} = 1\dfrac{1}{2} \\\\\)
So Will needs to travel a further \(1\dfrac{1}{2}\) miles to reach the park
Help please! Quick math question

Answers
\(\huge\mathfrak\red {Answer:}\)
If the angle above b is 54° then,
a = 54°(Corresponding angles of a parallel line)
b = 126°(Cause <b and 54° form a linear pair which is 180° and 180° -54° = 126°)
\(\mathfrak\purple {Hope\: this\: helps\: you...}\)
Expressed in simplest a + bi form, (7-3i) + (x - 2i)² - (4i + 2x²) is
Answers
Therefore, the expression (7-3i) + (x - 2i)² - (4i + 2x²) in the simplest a + bi form is: -2x² - 1 - (4x + 7i)
What are the different forms of linear equation?Linear Equation General Form Example
Slope intercept form y = mx + b y + 2x = 3
Point–slope form y – y1 = m(x – x1 ) y – 3 = 6(x – 2)
General Form Ax + By + C = 0 2x + 3y – 6 = 0
Intercept form x/a + y/b = 1 x/2 + y/3 = 1
As a Function f(x) instead of y f(x) = x + C f(x) = x + 3
The Identity Function f(x) = x f(x) = 3x
Constant Functions f(x) = C f(x) = 6
Let's start by expanding the square term (x - 2i)² using the formula for (a + b)²:
(x - 2i)² = x² - 4xi + 4i²
Note that i² = -1, so we can simplify this expression to:
(x - 2i)² = x² - 4xi - 4
Substituting this expression and the given values into the original expression, we get:
(7 - 3i) + (x² - 4xi - 4) - (4i + 2x²)
Grouping the real and imaginary terms, we get:
(7 - 4 - 2x²) + (-3i - 4i - 4x) + (x²)
Simplifying the real part, we get:
-2x² - 1
Simplifying the imaginary part, we get:
-7i - 4x
Learn more about Linear equations here:
brainly.com/question/11897796
#SPJ1
Which statement about geometric figures is true
Answers
Answer:
Geometric shapes are practically everywhere. No matter where you look, almost everything is made up of simpler geometry. A truss bridge is made primarily of rectangles, squares and triangles, for example. A snowman is made up of circles, with a cone-shaped carrot nose.
what the answer for this area?

Answers
Answer:
the answer is 105
Step-by-step explanation:
because 5×3=15 so 15×7 =105
Distribute to create an equivalent expression with the fewest symbols possible.
4(5+y) =4(5+y)
Answers
The equivalent expression of 4(5+y) by distributing is 20 + 4y.
How to find equivalent expression?In maths, an expression is a combination of numbers, variables, functions (such as addition, subtraction, multiplication or division etc.).
Two expressions are said to be equivalent if they have the same value irrespective of the value of the variable(s) in them.
In other words, two mathematical expressions are said to be equivalent if they yield the same result upon solving them.
Therefore, let's find the equivalent expression of 4(5 + y) by distributing it.
Hence,
4(5 + y) = 20 + 4y
learn more on equivalent expression here: https://brainly.com/question/29412493
#SPJ1
A total of 27 students are in your class. There are nine more males than females.
How many females are in your class?
Answers
the answer is actually 81
Answers
Answer:
okay i'll keep this in mind
Step-by-step explanation:
The graph below shows the solutions to which inequality?
A. x^2-3x+3 ≥0
B. x² + 3x-3 <0
C. x²-3x+3<0
D. x² + 3x-3>0
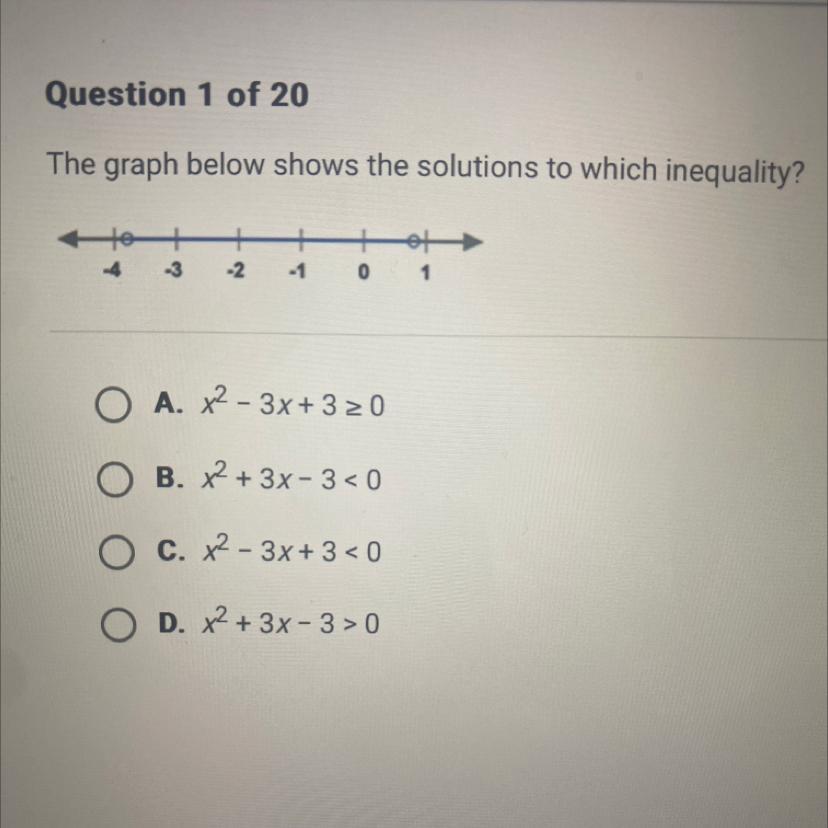
Answers
The inequality expression that corresponds to the solution of the inequality graph is x² + 3x - 3 < 0.
option B.
What is the solution of the inequality?The inequality expression that corresponds to the solution of the inequality graph is determined by simplifying the equations as follows;
The solution of the graph,
x > -4 and x < 1
The first equation with "≥" is ruled out because the graph doesn't have a thick dot.
Let's simplify the second expression;
x² + 3x - 3 < 0
solve using quadratic formula;
x > -3.79 or x < 0.79
The third expression is ruled out since its solution will be complex.
For the last expression;
x² + 3x - 3 > 0
x < -3.79 or x > 0.79
Thus, the correct inequality expression is x² + 3x - 3 < 0.
Learn more about inequality expression here: https://brainly.com/question/25275758
#SPJ1
3. You get three summer jobs to help you save for college expenses. In your job as a cashier,
you work 20 hours per week and earn $9.50 per hour. Your second and third jobs are at a local
hospital. There, you earn $9.00 per hour as a payroll clerk and $7.00 per hour as an aide. You
always work 10 hours less per week as an aide than you do as a payroll clerk. Your total weekly
salary depends on the number of hours you work at each job.
a. Determine the input and output variables for this situation.
b. Explain how you calculate the total amount earned each week.
c. If x represents the number of hours you work as a payroll clerk, represent the number of
hours you work as an aide in terms of x.
d. Write an equation that describes the total amount you earn each week. Use x to represent
the input variable and y to represent the output variable. Simplify the expression as much
as possible.
e. If you work 12 hours as a payroll clerk, how much will you make in one week?
f. What are the practical replacement values for x? Would 8 hours at your payroll job be a
realistic replacement value? What about 50 hours?
g. When you don't work as an aide, what is your total weekly salary?
Please help!
Answers
Hence the output variable (total weekly earnings) is a function of the input variable (number of hours worked as a payroll clerk) and may be expressed by the equation y = 16x + 120.
What is a Variable?A variable is anything that may be altered in the context of a mathematical notion or experiment. Variables are frequently denoted by a single symbol. .
a. Input variables: hours worked as a cashier, payroll clerk, and assistant.
The total amount earned each week is the output variable.
b. To determine the weekly total, multiply the number of hours worked at each job by the hourly rate and put them together. As a result, the equation would be:
Total weekly wage = (hours worked as a cashier x cashier hourly rate) + (hours worked as a payroll clerk x payroll clerk hourly rate) + (hours worked as an aide x rate per hour as an aide)
c. The amount of hours worked as an assistant is always 10 hours fewer than that of a payroll clerk. Therefore, if x denotes the number of hours worked as a payroll clerk, then the number of hours worked as an assistant may be denoted as (x - 10).
d. The equation describing the total money earned each week is as follows:
(20 x 9.5) + (x x 9) + ((x - 10) x 7) = y
This expression is simplified as follows:
y = 190 + 9x - 70 + 7x
y = 16x + 120
Hence the output variable (total weekly earnings) is a function of the input variable (number of hours worked as a payroll clerk) and may be expressed by the equation y = 16x + 120.
f. The realistic replacement values for x would be determined by the maximum number of hours you may work at each job as well as the amount of time available to work. Working 8 hours as a payroll clerk may be a reasonable substitute value if you have restricted availability, but 50 hours is unlikely.
g. If you do not work as an aide, you may calculate your total weekly income by setting the number of hours worked as an aide to zero in the calculation for the total amount earned each week. This results in:
y = 16x + 120 + 0
y = 16x + 120
As a result, the total weekly wage would be determined only by the number of hours performed as a cashier and payroll clerk.
To know more about variable visit:
https://brainly.com/question/2466865
#SPJ1
A tube of watercolor paints is $8.69, a paintbrush is $4.78, and a canvas is $6.32. If you pay with a $20 bill, how much money will the cashier give back to you?
Show your work & NO LINKS!
Answers
Answer:
0.21
Step-by-step explanation:
Answer:
$0.21
Step-by-step explanation:
The tube of watercolor paints costs
= $8.69
The paintbrush costs
= $4.78
And the canvas costs
= $6.32
Total amount
= $19.79
If we pay $20 the cashier will give back
= $20 - $19.79
= $0.21
Find the root of the equation. 9x^2-1-(3x-2)^2=0
Answers
Answer: 5/12
Step-by-step explanation:

Question below!
Please help!!!!

Answers
Step-by-step explanation:
Answer is in the pic above

Answer:
Step-by-step explanation:

A hotel room costs $435.92 for 4 nights. At the same rate, how much would it cost to rent the hotel room for 7 nights?
Answers
Answer:
basBdiqdia
Step-by-step explanation:
Answer:
$762.86
Step-by-step explanation:
$435.92/4 = $108.98
$108.98 · 7 = $762.86
Find the length of AC and the measures of a and 0
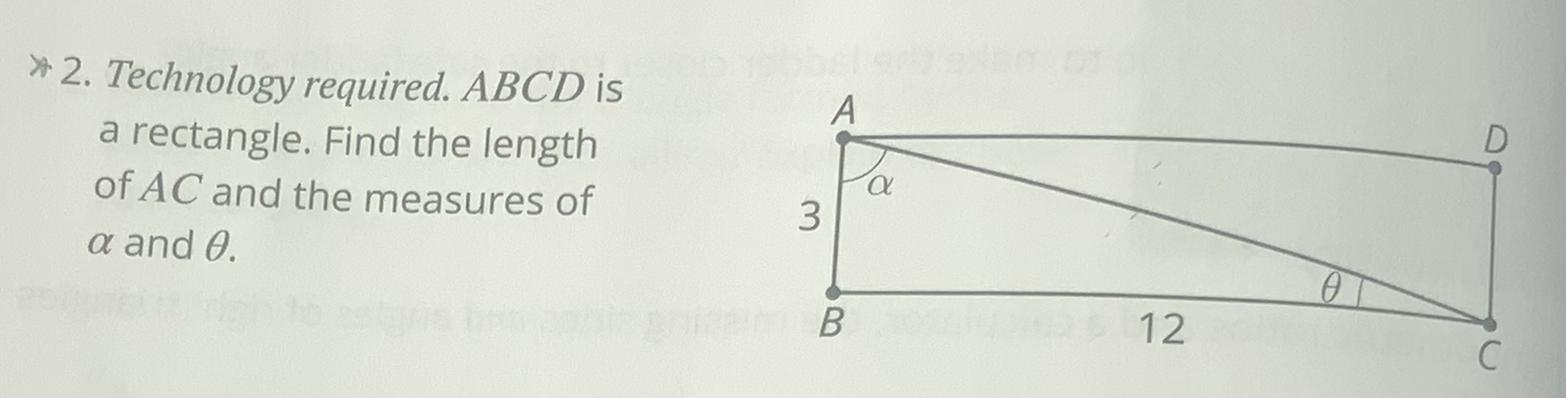
Answers
ANSWER:
AC = 3√ 17
α = 75.96°
Θ = 14.04°
STEP-BY-STEP EXPLANATION:
We can calculate the length of side AC by means of the Pythagorean theorem, just like this:
\(\begin{gathered} c^2=a^2+b^2 \\ \text{ in this case:} \\ (AC)^2=3^2+12^2 \\ (AC)^2=9+144 \\ AC=\sqrt[]{153} \\ AC=3\sqrt[]{17} \end{gathered}\)We can calculate the angles by applying the following trigonometric ratios:
\(\begin{gathered} \sin \alpha=\frac{12}{3\sqrt[]{17}} \\ \alpha=\arcsin \mleft(\frac{12}{3\sqrt{17}}\mright) \\ \alpha=75.96 \\ \\ \sin \theta=\frac{3}{3\sqrt[]{17}} \\ \theta=\arcsin \mleft(\frac{3}{3\sqrt{17}}\mright) \\ \theta=14.04 \end{gathered}\)What is the constant of proportionality in the equation y=5/4x
Answers
The constant of proportionality in the equation is 5/4
What is constant of proportionality?The constant connecting two given numbers in what is known in a proportional relationship is the constant of proportionality.
The constant of proportionality may also be referred to as the constant ratio, constant rate, unit rate, constant of variation, or even the rate of change.
In the problem, y = 5/4x
The constant term 5/4 as used in the equation is used t multiply the input x values to get the out put y values
The term helps in relating x to y
Learn more about constant of proportionality at:
https://brainly.com/question/27598477
#SPJ1
Need help with the question

Answers
Answer:
x = 0 or x = 1
Step-by-step explanation:
f(x) = |x| - 4
g(x) = x³ - 4
f(x) = g(x)
|x| - 4 = x³ - 4
Add 4 to both sides.
|x| = x³
x = x³ or -x = x³
x³ - x = 0 or x³ + x = 0
x(x² - 1) = or x(x² + 1) = 0
x = 0 or x + 1 = 0 or x - 1 = 0
x = 0 or x = -1 or x = 1
x = -1 does not work, so we discard that solution.
Answer: x = 0 or x = 1
Answer:
values of x: x = 1 and x = 0
Step-by-step explanation:
Given:
f(x)= |x| - 4g(x) = x³ - 4Want: x - values when f(x) = g(x)
f(x) = g(x) → |x| - 4 = x³ - 4positive interval x ≥ 0negative interval x < 0|x| - 4 = x³ - 4, the 4 cancel out on both sides
|x| = x³
|x| - x³ = x³ - x³
|x| - x³ = 0, x ≥ 0
-x - x³ = 0, x < 0
x = 0
x = -1, x ≥ 0
x = 1
x = 0, x < 0
The intersections are x = 0 and x = 1 and no solution
Learn more about Inequalities here: https://brainly.com/question/25275758
Looking at the table above ,
A. What would you consider as the independent variable in this situation ? Introduce the symbol/ name (x,t,...) you will use to represent this variable . Remember to include the units.
B. What is the dependent variable ? Introduce the symbol /name for this variable . Remember the units .

Answers
The independent Variable in the situation presented in the table is the temperature (T), which is measured in degrees Celsius (°C), and the dependent variable is the volume (V), which is measured in milliliters (mL).
The table above illustrates the relationship between the temperature of a substance and its volume. The independent variable is the temperature of the substance and the dependent variable is the volume of the substance.
The symbol or name used to represent the independent variable is "T" for temperature and its units are given as degrees Celsius or °C.The symbol or name used to represent the dependent variable is "V" for volume, and its units are given as milliliters or mL.
The temperature is the independent variable as it is being manipulated in the experiment while the volume is dependent on the temperature as it is changing based on the temperature.
An independent variable is a variable in an experiment that is being manipulated by the experimenter, while the dependent variable is the variable that is being measured in response to changes in the independent variable.
In summary, the independent variable in the situation presented in the table is the temperature (T), which is measured in degrees Celsius (°C), and the dependent variable is the volume (V), which is measured in milliliters (mL).
For more questions on Variable .
https://brainly.com/question/28248724
#SPJ8
table, averages.....
Answers
Given:
The table contains the years as 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020.
The sales values are 287, 332, 367, 392, 407, 412, 407, 392, 367.
The objective is to find the average rate of change of annual sales between 2012 and 2013.
Consider the intervals as a = 2012 and b= 2013.
Then, the value of f(a) = 287 and f(b) = 332.
To find the average rate of change, the formula is,
\(\begin{gathered} \text{Average rate of change=}\frac{Change\text{ in output}}{Chang\text{e in input}} \\ =\frac{f(b)-f(a)}{b-a} \end{gathered}\)Let's substitute the given values in the above formula.
\(\begin{gathered} \text{Average rate of change = }\frac{332-287}{2013-2012} \\ =\frac{45}{1} \\ =45 \end{gathered}\)Hence, the average rate of change of sales over the interval 2012 and 2013 is 45 millions of dollar per year.
An elevator has a maximum capacity of 950 pounds, and there must be an attendant working in the elevator at all times. A customer asks for the range of the number of people that the elevator can hold, not including the attendant. Assume that the average person weighs 155 pounds. Answer the customer's question. Include in your answer the equation or inequality that you used to find the solution.
Answers
Answer:
6 lol just do 155x 6 people
Answer:
the answer is 6 that's not including the attendant
Step-by-step explanation:
do 950/6 and that should help you sorry if this does not help you it is hard to explain. (I'm just not good at explaining)