Find the measure of x.
78.3°
115
X =
[?]
Round your answer to the nearest tenth.
![Find The Measure Of X.78.3115X =[?]Round Your Answer To The Nearest Tenth.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/KeMBWCMMxzhTEabFljxEUJppdipBTXug.png)
Answers
![Find The Measure Of X.78.3115X =[?]Round Your Answer To The Nearest Tenth.](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/wrwdGQNzFQJmvh5YaSehNsXCs0ZKxOkN.png)
Related Questions
An experimenter would like to construct a 99% confidence interval with a width at most 0. 5 for the average resistance of a segment of copper cable of a certain length. If the experimenter knows that the standard deviation of such resistances is 1. 55. How big a sample should the experimenter take from the population? what happens if the standard deviation and the width of the confidence interval are both doubled?.
Answers
A big sample that should the experimenter take from the population is 256 and if the standard deviation and the width of the confidence interval are both doubled then the sample is also 256.
In the given question,
The confidence level = 99%
Given width = 0.5
Standard deviation of resistance(\(\sigma\))= 1.55
We have to find a big sample that should the experimenter take from the population and what happens if the standard deviation and the width of the confidence interval are both doubled.
The formula to find the a big sample that should the experimenter take from the population is
Margin of error(ME) \(=z_{\alpha /2}\frac{\sigma}{\sqrt{n}}\)
So n \(=(z_{\alpha /2}\frac{\sigma}{\text{ME}})^2\)
where n=sample size
We firstly find the value of ME and \(z_{\alpha /2}\).
Firstly finding the value of ME.
ME=Width/2
ME=0.5/2
ME=0.25
Now finding the value of \(z_{\alpha /2}\).
Te given interval is 99%=99/100=0.99
The value of \(\alpha\) =1−0.99
The value of \(\alpha\) =0.01
Then the value of \(\alpha /2\) = 0.01/2 = 0.005
From the standard table of z
\(z_{0.005}\) =2.58
Now putting in the value in formula of sample size.
n\(=(2.58\times\frac{1.55}{0.25})^2\)
Simplifying
n=(3.999/0.25)^2
n=(15.996)^2
n=255.87
n≈256
Hence, the sample that the experimenter take from the population is 256.
Now we have to find the sample size if the standard deviation and the width of the confidence interval are both doubled.
The new values,
Standard deviation of resistance(\(\sigma\))= 2×1.55
Standard deviation of resistance(\(\sigma\))= 3.1
width = 2×0.5
width = 1
Now the value of ME.
ME=1/2
ME=0.5
The z value is remain same.
Now putting in the value in formula of sample size.
n\(=(2.58\times\frac{3.1}{0.5})^2\)
Simplifying
n=(7.998/0.5)^2
n=(15.996)^2
n=255.87
n≈256
Hence, if the standard deviation and the width of the confidence interval are both doubled then the sample size is 256.
To learn more about confidence interval link is here
brainly.com/question/24131141
#SPJ4
Which number line shows the solution to w - 2 ≤ 8? *
(don't delete my question)

Answers
Answer:
closed circle going left from 10
Step-by-step explanation:
B (* ̄3 ̄)╭
____ : referring to the fact that the distance between two or more points is equal.
Answers
The term that refers to the fact that the distance between two or more points is equal is "equidistant".
In geometry, the concept of equidistance is important when dealing with circles, which are sets of points that are equidistant from a single point called the center. This property is what allows circles to be defined in terms of their radius, which is the distance between the center and any point on the circle.
Equidistance is also important in other areas of mathematics and science. For example, in physics, equidistant points can be used to define a plane or surface that is perpendicular to a given line or axis. This is useful in many applications, such as designing electronic circuit boards or constructing buildings.
The concept of equidistance is not limited to mathematics and science, however. It can also be applied in everyday life. For instance, if you are planning a road trip and want to visit several destinations that are equidistant from your starting point, you can use this information to help plan your route and estimate your travel time.
for such more question on equidistant
https://brainly.com/question/15683939
#SPJ11
Write a unit rate for the situation.
1080 miles on 15 gallons
Answers
Step by step Explanation:
Divide 1080 by 15 and divide 15 by 15. You get 72 and one.
Hope me helped!
Answer:
72 miles=1 gallon
Step-by-step explanation:
Divide 1080 by 15 and divide 15 by 15. You get 72 and one.
Which measure is of an angle that is coterminal with a 95° angle?
Answers
Answer:
95° - (1,080 n) °, for any integer n
Step-by-step explanation:
Co-terminal angle are those angles who share the same initial side and terminal sides,
And, these angles are obtained by adding or subtracting the multiple of 360°,
That is, if Ф is an angle,
Then its co-terminal angles are,
Ф + 360 n
Where, n is any integer (negative or positive)
Here, Ф = 95°,
Since, n is an integer,
⇒ - 3n is an integer,
Thus, the co-terminal angles of 95° are,
95° + 360° (-3n)
= 95° - (1080 n) °; for any integer n.
Step-by-step explanation:
Hope this helps!~
And I hope this is what you where looking for.
Good Luck!~
Answer:
B. 95° – (1,080n)°, for any integer n
Step-by-step explanation:
Correct on EDGE 2021!
For each value of w, determine whether it is a solution to -54 <7w-5.

Answers
Answer:
All in order:
YES
NO
NO
NO
Step-by-step explanation:
-54 ≤ 7(-7) - 5 YES because the sign says greater than or equal to (in the image)
-54 ≤ 7(5) - 5 NO
-54 ≤ 7(7) - 5 NO
-54 ≤ 7(-9) - 5 NO
a carpenter and his assistant can do a piece of work in 3 days. if the carpenter himself could do the work alone in 5 days, how long would the assistant take to do the work alone?
Answers
The number of days spent or taken by assistant with work efficiency of 2 units per day to do the work alone is equals to the 7.5 days.
We have provide that there is a carpenter and his assistant can do a piece of work.
Number of days taken by both carpenter and his assistant to do a piece of work = 3 days.
Number of days taken by carpenter and to do the same piece of work alone = 5 days.
We have to determine number of taken by assistant and to do the same piece of work alone.
Let the required number of days that the assistant take to do the work alone be 'x days'. As we know, total available work units = LCM (3,5) = 15 units
Ability or efficiency of a person or man is calculated by dividing the total work units to the number of working days spent to do the work.
Now, Ability or efficiency of both carpenter and his assistant work together = 15/5
= 3 units/day
Similarly, Ability or efficiency of carpenter = 15/3
= 5 units/day
So, Ability or efficiency of assistant= 5 - 3 = 2 -(1)
Using efficiency formula, efficiency of assistant
= 15/x --(2)
from (1) and(2), 15/x = 2
=> 2x = 15
=> x = 7.5
Hence, required number of days are 7.5 days.
For more information about work-efficiency formula, refer:
#SPJ4
Find the rate of change of the line by completing parts (a) and (b).
Select any two points on the line to label as P and R. Name their coordinates.
1

Answers
Answer:
The rate of change is 1/2
Step-by-step explanation:
Formula:
y-y/x-x
The two points i chose were (-1,1) and (1,1)
You plug them in:
1-0/ 1 - (-1)
leaving you with 1/2
Which pair of figures shows two shapes that each have opposite sides of equal length?

Answers
The box with rhombus and rectangle are the two shapes that each have opposite sides of equal length.
In the options given, the first box has a rhombus and a rectangle.
We know that a rhombus has all four sides of equal length.
This means that opposite sides are of equal length.
We also know that a rectangle has opposite sides of equal length.
In this option, both of them have opposite sides of equal length.
So, this is the correct answer.
The second box has a quadrilateral and a trapezoid.
The trapezoid is a quadrilateral with one pair of opposite sides parallel, but the length of the sides is not equal. A trapezoid might have right angles, then it is called a right trapezoid.
A quadrilateral is a two-dimensional shape that has 4 sides.
In this option, both shapes do not have opposite sides of equal length. So, this is not the right answer to the given question.
The third box has a trapezoid and a parallelogram.
A trapezoid is a quadrilateral with one pair of opposite sides parallel, but the length of the sides is not equal. A trapezoid might have right angles, then it is called a right trapezoid.
We know that a parallelogram has opposite sides of equal length.
In this option, one shape has opposite sides equal but not the other.
So, this is not the right answer to the given question.
The fourth box has a rhombus and trapezoid.
We know that a rhombus has all four sides of equal length.
This means that opposite sides are of equal length.
A trapezoid is a quadrilateral with one pair of opposite sides parallel, but the length of the sides is not equal. A trapezoid might have right angles, then it is called a right trapezoid.
In this option, one shape has opposite sides equal but not the other.
So, this is not the right answer to the given question.
Learn more at:
https://brainly.com/question/8823615
#SPJ9
Pls po i really need help ASAP. I'll mark brainliest who answered po.
STATISTICS:

Answers
A) Mean = 5.8
Median = 5.5
mode = 5
B) Mean = 127.5
Median = 28
mode = 11 -12 scores
Solving for the mean, median and mode:3, 4, 5, 5, 5,6,6, 7, 8,9
A) Mean = 3+ 4+ 5+ 5+ 5+ 6+ 6+ 7 + 8 + 9
10
Mean = 58/10
= 5.8
3, 4, 5, 5, 5,6,6, 7, 8,9
Median = 5 + 6
2
Median = 11/2
= 5.5
3, 4, 5, 5, 5,6,6, 7, 8,9
mode = 5
B) Scores 1 -10, 11- 20, 21 -30, 31-40, 41 -50
Mid- scores 5.5, 15.5 , 25.5 ,35.5 , 45.5
Frequencies 8 , 14 , 12 , 9 , 7
Mean of group data = Sum of (Interval midpoint * Freq )
Total Frequency
Mean of group data = 5.5 + 15.5 + 25.5 + 35.5 + 45.5
50
Mean of group data = 127.5
Median = Calculate a running total of the frequencies - the first interval that is above half the total contains the median.
Median = 50 - ( 8 + 14)
Median = 50 - 22
= 28
Mode = The largest frequency and the corresponding value is the modal value or modal class.
Mode = 11 -12 scores
Learn more about Mean on
https://brainly.com/question/30112112
#SPJ1
(−2 3/2)^2
KHAN ACADEMY (EXPONENTS WITH NEGATIVE FRACTIONAL BASE)
Answers
The values of the given expression having exponent with negative fractional base i.e. \(-2^{(3/2)^2}\\\) is evaluated out to be 16/9.
First, we need to simplify the expression inside the parentheses using the rule that says "exponents with negative fractional base can be rewritten as a fraction with positive numerator."
\(-2^{(3/2)^2}\) = (-2)² × (2/3)²
Now, we can simplify the expression further by solving the exponent of (-2)² and (2/3)²:
(-2)² × (2/3)² = 4 × 4/9 = 16/9
Therefore, the value of the given expression \(-2^{(3/2)^2}\\\) is 16/9.
Learn more about Exponents :
https://brainly.com/question/30441288
#SPJ4
The question is :
What is the value of the expression \(-2^{(3/2)^2}\) ?
ASAP, REALLY EASY If x = -3 then what is -x
Answers
Answer:
3
because it says -3
so yeah
atleast i hope Im so bad at math
Please heart this I need to get closer to earning the message in brainly !!
6a+5b=4.54
3a+7b=3.17
Answers
\(6a = 4.54 - 5b \\ a = \frac{227}{300} - \frac{5}{6} b \\ 6a = 4.54 - 5b \\ a = \frac{227}{300} - \frac{5}{6} \\ 3( \frac{227}{300} - \frac{5}{6} b) + 7b = 3.17 \)
\( 3( \frac{227}{300} - \frac{5}{6} b) + 7b = 3.17 \\ \frac{227}{100} - \frac{5}{2}b + 7b = 3.17 \\ \frac{9}{2}b = 0.9 \\ b = 0.2 \\ a = 0.59\)
What is the Length of this diameter?

Answers
The length of the diameter is 18 meters
Calculating the length of the diameter
from the question, we have the following parameters that can be used in our computation:
SA = 1017.36
The shape is a sphere
So, we have
SA = 4πr²
Substitute the known values in the above equation, so, we have the following representation
4πr² = 1017.36
So, we have
r² = 80.96
Take the square root
r = 9
Multiply by 2
d = 18
Hence, the diameter is 18 meters
Read more about surface area at
https://brainly.com/question/16519513
#SPJ1
How do you find the slope of a perpendicular line with an equation and point?
Answers
First, by solving for y, convert the equation of the given line into slope-intercept form y=mx+c .You obtain the slope of the equation as m. Since the slopes of perpendicular lines are negative reciprocal, the slope of the line we're looking is the negative reciprocal of the perpendicular equation.
By entering the supplied point into the formula y = mx + b and solving for b, we arrive at the value of b. Consequently, the line's equation is formed.
A line's slope in mathematics is defined as the ratio of the change in the y coordinate to the change in the x coordinate.
Both the net change in the y-coordinate and the net change in the x-coordinate are denoted by Δy and Δx, respectively.
m = y/x = y/x = change in y/change in x
where "m" represents a line's slope.
Additionally, the slope of the line may be shown as
tan θ = Δy/Δx
A line's slope often indicates the steepness and direction of the line.
To know more about slope of line refer to:
brainly.com/question/29082598
#SPJ4
m = y/x = y/x = change in y/change in x
where "m" represents a line's slope.
Additionally, the slope of the line may be shown as
tan θ = Δy/Δx
"1. In which of the following categories of problems an 8-puzzle
problem can be placed? Discuss with appropriate reasoning.
Pathfinding problems
State finding problems
Decomposable problems
Pre"
Answers
The 8-puzzle problem can be categorized as a "Pathfinding problem."
The 8-puzzle is a classic problem in artificial intelligence and computer science. It involves a 3x3 grid with eight numbered tiles and one empty space. The objective is to rearrange the tiles from an initial configuration to a goal configuration by sliding them into the empty space.
The reason why the 8-puzzle problem is classified as a pathfinding problem is that it involves finding a sequence of moves or actions to reach a desired state or goal. In this case, the desired state is the goal configuration of the puzzle. The problem requires determining the optimal sequence of moves that lead to the goal state while considering the constraints and limitations of the puzzle.
Pathfinding problems involve finding the shortest or optimal path from a starting point to a goal or destination. In the 8-puzzle problem, the empty space serves as the movable "agent" that can slide adjacent tiles. The objective is to find the shortest sequence of moves or actions to transform the initial configuration into the goal configuration, effectively finding a path to the solution.
Therefore, due to its nature of finding an optimal sequence of moves to reach a goal state, the 8-puzzle problem can be categorized as a pathfinding problem.
Learn more about limitations here:
brainly.com/question/12207539
#SPJ11
Sarah's brother is 12 less than twice her age. If Sarah is 16, what equation represents this situation?
Answers
The equation that can be used to represent the ages of Sarah and his brother will be 2x - 12 = 16.
How to solve the equationFrom the question given, Sarah's brother is 12 less than twice her age and Sarah is 16.
Let Sarah's age be represented by x.
Therefore, the equation to represent the situation will be:
= (2 × x) - 12 = 16
2x - 12 = 16
2x = 16 + 12.
2x = 28
x = 28/2 = 14
Sarah is 14 years.
Learn more about equations on:
https://brainly.com/question/13763238
The probability density function of a continuous random variable X is
f(x) = { kx2 0≤x≤2
0 otherwise
(a) What value should k be in order for f(x) to be a probability density function?
(b) Calculate P (1 < X ≤1.5) and P (X > 1.5) using the value of k that you find.
Answers
(a) In order for f(x) to be a probability density function, it must satisfy two conditions: non-negativity and the integral over the entire range should equal 1.
For the given function, f(x) = kx^2, we need to find the value of k that satisfies these conditions.
The integral of f(x) from 0 to 2 should equal 1:
∫[0,2] kx^2 dx = 1
Integrating kx^2 with respect to x gives:
(k/3) * x^3 | [0,2] = 1
Substituting the limits of integration, we have:
(k/3) * 2^3 - (k/3) * 0^3 = 1
(8k/3) = 1
Solving for k, we find:
k = 3/8
Therefore, the value of k should be 3/8 for f(x) to be a probability density function.
(b) P (1 < X ≤1.5) and P (X > 1.5) is equal to 27/32 and 5/32.
To calculate P(1 < X ≤ 1.5), we need to integrate f(x) over the interval [1,1.5]:
∫[1,1.5] (3/8) * x^2 dx
Integrating (3/8) * x^2 with respect to x gives:
(3/8) * (x^3/3) | [1,1.5]
Substituting the limits of integration, we have:
(3/8) * ((1.5)^3/3) - (3/8) * ((1)^3/3)
Simplifying the expression, we get:
(3/8) * (3.375 - 1/3)
(3/8) * (3.375 - 1/3) = (27/32)
Therefore, P(1 < X ≤ 1.5) is equal to 27/32.
To calculate P(X > 1.5), we need to find the complement of P(1 < X ≤ 1.5), which is equal to 1 - P(1 < X ≤ 1.5):
1 - (27/32) = (32/32) - (27/32) = (5/32)
Therefore, P(X > 1.5) is equal to 5/32.
To know more about probability density function refer here:
https://brainly.com/question/31039386?#
#SPJ11
A cylindrical bioreactor of diameter 3 m has four baffles. A Rushton turbine mounted in the reactor has a diameter of one-third the tank diameter. The liquid height is equal to the tank diameter, and the density of the fluid is approximately 1 g cm −3. The reactor is used to culture an anaerobic organism that does not require gas sparging. The broth can be assumed Newtonian. As the cells grow, the viscosity of the broth increases. The proportionality constant, k 1 is 70 , and the power number, N ′P is 5.0 for the impeller and the tank geometries. (a) The stirrer is operated at a constant speed of 90rpm. Estimate the mixing time when the viscosity is approximately that of water. (b) The viscosity reaches a value of 1000 times greater than water. (i) What stirrer speed is required to achieve turbulence? (ii) Estimate the power required to achieve turbulence. (iii) What is the power per unit volume required for turbulence? Is it comparable to average power consumption per unit volume for industrial bioreactors?
Answers
(a) The estimated mixing time when the viscosity is approximately that of water and the stirrer is operated at a constant speed of 90 rpm is approximately 10.48 seconds.
(b) (i) To achieve turbulence when the viscosity reaches a value of 1000 times greater than water, a stirrer speed of approximately 528.67 rpm is required.
(ii) The power required to achieve turbulence is approximately 35.14 kW.
(iii) The power per unit volume required for turbulence is approximately 1.95 W/m^3.
(a) The mixing time when the viscosity is approximately that of water, assuming a constant stirrer speed of 90 rpm, can be estimated using the following steps:
⇒ Calculate the impeller Reynolds number (Re):
Re = (N′P / k1) × (N / N1)^2
We have,
N′P = 5.0 (power number)
k1 = 70 (proportionality constant)
N = 90 rpm (stirrer speed)
N1 = 1 (reference stirrer speed)
Plugging in the values:
Re = (5.0 / 70) × (90 / 1)^2
≈ 910.71
⇒ Calculate the mixing time (tm):
tm = (0.08 × ρ × D^2) / (μ × N′P × Re)
We have,
ρ = 1 g/cm^3 (density of the fluid)
D = 3 m (diameter of the tank)
μ ≈ 0.001 Pa·s (viscosity of water at room temperature)
Plugging in the values:
tm = (0.08 × 1 × 3^2) / (0.001 × 5.0 × 910.71)
≈ 10.48 seconds
Therefore, the estimated mixing time when the viscosity is approximately that of water is approximately 10.48 seconds.
(b) (i) To achieve turbulence when the viscosity reaches a value of 1000 times greater than water, the stirrer speed required can be estimated by equating the impeller Reynolds number (Re) to the critical Reynolds number (Recr) for transition to turbulence. The critical Reynolds number for this system is typically around 10^5.
Recr = 10^5
Setting Recr equal to the Re equation from part (a):
10^5 = (5.0 / 70) × (N / 1)^2
Solving for N:
N = √((10^5 × k1 × N1^2) / N′P)
= √((10^5 × 70 × 1^2) / 5.0)
≈ 528.67 rpm
Therefore, a stirrer speed of approximately 528.67 rpm is required to achieve turbulence.
(ii) The power required to achieve turbulence can be estimated using the following equation:
P = N′P × ρ × N^3 × D^5
We have,
N′P = 5.0 (power number)
ρ = 1 g/cm^3 (density of the fluid)
N = 528.67 rpm (stirrer speed)
D = 3 m (diameter of the tank)
Plugging in the values:
P = 5.0 × 1 × (528.67 / 60)^3 × 3^5
≈ 35141.45 watts
Therefore, the power required to achieve turbulence is approximately 35.14 kW.
(iii) The power per unit volume required for turbulence can be calculated by dividing the power by the tank volume (V):
P/V = P / (π/4 × D^2 × H)
We have,
P = 35.14 kW (power required)
D = 3 m (diameter of the tank)
H = 3 m (liquid height)
Plugging in the values:
P/V = 35.14 × 10^3 / (π/4 × 3^2 × 3)
≈ 1.95 W/m^3
The power per unit volume required for turbulence is approximately 1.95 W/m^3.
To know more about power consumption per unit volume in bioreactors, refer here:
https://brainly.com/question/32435602#
#SPJ11
for the following measurement, find the measurement that is the least accurate:
a. 208 m; b.18050 m;
c. 0.08 m; d.0.750 m; d.12.0 m.
Answers
The least accurate measurement among the options provided is 18050 m.Therefore, among the given options, 18050 m is the least accurate measurement due to its higher number of significant figures.
To determine the least accurate measurement, we need to consider the number of significant figures in each measurement. The measurement with the fewest significant figures indicates lower accuracy.
Among the options given:
a. 208 m has three significant figures.
b. 18050 m has five significant figures.
c. 0.08 m has two significant figures.
d. 0.750 m has three significant figures.
e. 12.0 m has three significant figures.
The measurement with the least accurate value is 18050 m because it has the highest number of significant figures among the options. A higher number of significant figures suggests a greater level of precision and accuracy in the measurement.
Significant figures represent the digits in a number that contribute to its precision. They include all the non-zero digits and any zeros that appear between non-zero digits or after a decimal point. In this case, the measurement 18050 m has five significant figures, indicating a high level of precision and accuracy.
On the other hand, measurements with fewer significant figures imply less precision and accuracy. For example, the measurement 0.08 m has only two significant figures, suggesting less certainty in the measurement compared to 18050 m.
To learn more about Significant figures : brainly.com/question/29153641
#SPJ11
I need this ASAP please I’ll mark you brainliest if you answer for me correctly

Answers
Answer:
y - 3 = -(x + 1)
y - 3 = -x - 1
y = -x + 2
Answer:
Pick options, 1,2,3,4 but DO NOT select option 5!!!
Step-by-step explanation:
The basic equation is y=mx+b where slope is m and b is the y intercept.
So our y intercept for this equation is 2. The line has a negative slope bc as increases, y decreases. (The line is pointing down.) Those are two good clues to start.
Let's calc the slope. slope = rise/run = (y2-y1)/(x2-x1)
(-1,3) and (1,1) are shown on the graph
slope = (3-1)/(-1-1)
= 2/-2 = -1
Slope = -1
Our equation is now y=-x+2
So let's find everything that equals y=-x+2
y-3 = -x-1 is the same as
y = -x+2
So pick the first option, y-3 = -x-1
(y+1) = -(x-3)
y+1 = -x+3
y=-x+2
So pick the 2nd option, (y+1) = -(x-3)
(y-3) = -(x+1)
y-3 = -x-1
y=-x-1+3
y=-x+2
So pick the 3rd option, (y-3) = -(x+1)
We already know to pick the 4th option, y=-x+2
(y-3) = (x-1)
y= x-1+3
y=x-2
DON'T PICK THE 5th option, because this has the wrong slope and wrong intercept!
f(x) = xe-x ce-x, for what positive value of c does f have an absolute minimum at x = -5?
Answers
The positive value of c that makes the function f(x) = xe^(-x)ce^(-x) have an absolute minimum at x = -5 is approximately 16.05.
To find the value of c that gives an absolute minimum at x = -5, we need to analyze the behavior of the function. First, we differentiate f(x) with respect to x to find the critical points. The derivative of f(x) is f'(x) = -x^2e^(-2x)ce^(-x). Setting f'(x) = 0 and solving for x, we find x = 0 as a critical point.
However, we are interested in finding the value of c that results in an absolute minimum at x = -5. Plugging x = -5 into f(x), we get f(-5) = -5e^(5)c^(-5)e^(5). Since e^5 is positive, to minimize f(-5), c should be as large as possible. Taking the limit as c approaches infinity, we find that f(-5) approaches 0.
Therefore, c should be a large positive value. Calculating the exact value, we find c ≈ 16.05 gives an absolute minimum at x = -5 for the function f(x).
Learn more about derivative here:
https://brainly.com/question/29020856
#SPJ11
in a quadrilateral abcd the bisector of angle c and angle d meet at e. if angle a =70°and b=100°,find the measure of angle ced
Answers
Answer:
Step-by-step explanation:
Let CE and DE be the bisectors of ∠C and ∠D respectively. Then, ∠1 = 1/2∠C and ∠2 = 1/2∠D
In △DEC, we have
→ ∠1 + ∠2 + ∠CED = 180° [Sum of angles of a triangle]
→ ∠CED = 180° - (∠1 + ∠2). .....(i)
Again, the sum od the angles of a quadrilateral is 360°.
∴ ∠A + ∠B + ∠C + ∠D = 360°
→1/2(∠A + ∠B) + 1/2∠C + 1/2∠D = 180°
→1/2(∠A + ∠B) + ∠1+ ∠2 = 180°
→1/2(∠A + ∠B) = 180° - (∠1+ ∠2)....(ii)
From (i) and (ii), we get 1/2(∠A + ∠B) = ∠CED
Hence, ∠A + ∠B = 2∠CED
pleasssseeee!!!!!!!!!!!
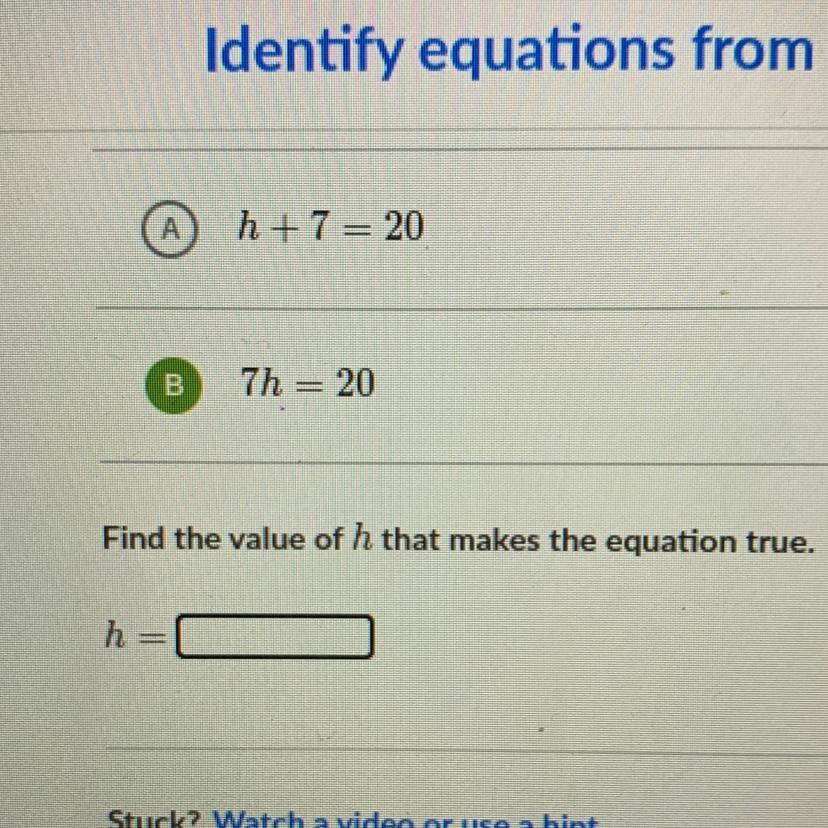
Answers
Answer:
h= the number 7 duh-
Step-by-step explanation:
In the kite picture above, find all the missing measures.
M<1=
M<2=
M<3=

Answers
Answer:
90
51
39
Step-by-step explanation:
hope this helps u have a great day
Answer:
opposite angles are ≈ diagonals of a kite are ⊥
∠1=90°
∠2=51°
∠3= 90°-51°=39°
∠3=39°
\(----------\\hope ~ it ~ helps\\\\have ~ a ~ great~ day.\)
Which of the following set of hypotheses is used to test if the mean of the first population is smaller than the mean of the second population, using matched-paired sampling?
H0: µ1 – µ2 ≤ 0, HA: µ1 – µ2 > 0
H0: µ1 – µ2 ≥ 0, HA: µ1 – µ2 < 0
H0: µD ≤ 0, HA: µD > 0
H0: µD ≥ 0,HA: µD < 0
Answers
The correct option H0: µD ≥ 0,HA: µD < 0, is used to determine whether the first population's mean is lower than the second population's mean, a set of hypotheses.
Explain the term matched-paired sampling?Paired testing, commonly referred to as auditing, is a practical and easy technique to determine whether and how discrimination is present.
In a paired exam, two individuals are given fictional identities and credentials that are equivalent in all significant ways.Each member of such a sample is paired with a matching member in every sample by comparison to characteristics other than those that are now the subject of the research. This results in a pair or set of matched samples.By "removing" the potential impacts of other variables, matching aims to produce better estimates of differences.The participants in matched samples (also known as matched pairs, paired samples, or dependent samples) were paired up so that they share all characteristics except the one that is being studied.Thus, µD ≥ 0,HA: µD < 0, is used to determine whether the first population's mean is lower than the second population's mean, a set of hypotheses.
To know more about the matched-paired sampling, here
https://brainly.com/question/13777653
#SPJ4
PLEASE HELP ASAP WILL GIVE 75 POINTS AND BRAINLIEST TO FIRST ANSWER!!!!
Imagine you work at a cola processing plant doing data entry and produce counts. You are doing an empty can count and come up with 1,000 cans. However, the computer system says there are 10,000 cans. After visually confirming that there are only 1,000, you check to see who last entered the value in the computer and discover it is your boss Ms. Strictlend. After triple checking your count you realize Ms. Strictlend made a mistake.
Write an email to Ms. Strictlend. Address her as you would a professional and explain the problem including the mistake she most likely made. Use as many words as you need to communicate the information without being fired.
Answers
Answer:
Step-by-step explanation:
Dear Ms Striclend,
I don’t think you meant to, but you made a mistake putting in the value for the computer system. Can you please explain to me how you made the mistake?
Thanks!
my name
differentiate between the Markov analysis and replacement chart and when it is appropriate to use either approach?
Answers
Markov analysis is used for analyzing the performance and reliability of complex systems, while replacement charts are used for optimizing the replacement timing of deteriorating assets.
Markov Analysis:
Markov analysis is a probabilistic model that is used to predict the future state of a system based on its current state.
It involves the use of Markov chains to model the transitions between different states of a system over time.
Markov analysis is commonly used when the equipment or system under consideration can be in multiple states with varying probabilities of transition.
It is suitable for analyzing systems that have a continuous or non-repairable nature, such as complex machinery, infrastructure, or systems with multiple failure modes.
The primary objective of Markov analysis is to assess the reliability, availability, and performance of the system and make decisions regarding maintenance, replacement, or repair strategies.
Replacement Chart:
A replacement chart, also known as a replacement model or replacement policy, is a decision-making tool used to determine the optimal time to replace a piece of equipment or system.
It involves comparing the costs associated with continuing to use the existing equipment (including maintenance and repair costs) with the costs of replacing it.
The replacement chart provides a visual representation of the costs over time and helps identify the point at which replacement becomes more cost-effective than continued use.
Replacement charts are commonly used for assets that are subject to wear and tear, aging, or deterioration over time, such as vehicles, machinery, or equipment with a defined lifespan.
The primary objective of a replacement chart is to minimize costs associated with the asset's life cycle by optimizing the replacement timing.
Learn more about optimizing here:
https://brainly.com/question/29521416
#SPJ11
What is an approximate average rate of change of the graph from X =22 and x = 26
Answers
Answer:
it is (22+26)/2=24
Step-by-step explanation:
At the beginning of the month Khalid had $25 in his school cafeteria account. Use a variable to
represent the unknown quantity in each transaction below and write an equation to represent
it. Then, solve each equation. Please show ALL your work.
1. In the first week he spent $10 on lunches: How much was in his account then?
There was 15 dollars in his account
2. Khalid deposited some money in his account and his account balance was $30. How
much did he deposit?
he deposited $15
3. Then he spent $45 on lunches the next week. How much was in his account?
Answers
1. In the first week, Khalid had $15 in his account.
2. Khalid Deposited $15 in his account.
3. After spending $45 the following week, his account has a deficit of $30.
1. In the first week, Khalid spent $10 on lunches. Let's represent the unknown quantity, the amount in his account at that time, as 'x'. The equation representing this situation is:
$25 - $10 = x
Simplifying, we have:
$15 = x
Therefore, there was $15 in his account then.
2. Khalid deposited some money in his account, and his account balance became $30. Let's represent the unknown deposit amount as 'y'. The equation representing this situation is:
$15 + y = $30
To find 'y', we can subtract $15 from both sides:
y = $30 - $15
y = $15
Therefore, Khalid deposited $15 in his account.
3. In the following week, Khalid spent $45 on lunches. Let's represent the amount in his account at that time as 'z'. The equation representing this situation is:
$15 - $45 = z
Simplifying, we have:
-$30 = z
The negative value indicates that Khalid's account is overdrawn by $30. Therefore, there is a deficit of $30 in his account.
1. In the first week, Khalid had $15 in his account.
2. Khalid deposited $15 in his account.
3. After spending $45 the following week, his account has a deficit of $30.
To know more about Deposited .
https://brainly.com/question/29209369
#SPJ8