Find the median, first quartile, third quartile, and interquartile rang of the data.
20, 12, 14, 22, 18, 21, 24, 15
Answers
The median of the given data set is 19, the first quartile is 14.5, the third quartile is 21.5, and the interquartile range is 7.
To find the median, first quartile, third quartile, and interquartile range of the given data, we need to arrange the data in order from smallest to largest:
12, 14, 15, 18, 20, 21, 22, 24
The median is the middle value of the data set. Since there are an even number of values in this data set, the median is the average of the two middle values:
Median = (20 + 18)/2 = 19
The first quartile (Q1) is the median of the lower half of the data set, and the third quartile (Q3) is the median of the upper half of the data set.
Q1 = median of 12, 14, 15, and 18
Q1 = (15 + 14)/2 = 14.5
Q3 = median of 20, 21, 22, and 24
Q3 = (21 + 22)/2 = 21.5
The interquartile range (IQR) is the difference between the third and first quartiles:
IQR = Q3 - Q1
IQR = 21.5 - 14.5
IQR = 7
Therefore, the median is 19, the first quartile is 14.5, the third quartile is 21.5, and the interquartile range is 7.
To learn more about median please click on below link
https://brainly.com/question/28060453
#SPJ1
Related Questions
At the tri-county track meet Jada won the 100 meter race in 12 9/10 seconds. The runner up finished in 13 1/10 seconds how many seconds faster was Jada then the funner up?
Answers
We have
\(\begin{gathered} 12\text{ }\frac{9}{10}\text{ = 12+}\frac{9}{10}\text{ = }\frac{120}{10}+\frac{9}{10}=\frac{129}{10} \\ 13\text{ }\frac{1}{10}=13+\frac{1}{10}=\frac{130}{10}+\frac{1}{10}=\frac{131}{10} \end{gathered}\)Then, the diference is
\(\frac{131}{10}-\frac{129}{10}=\frac{2}{10}=\frac{1}{5}\)So, Jada was 1/5 seconds faster than the second place.
Find the nth Taylor polynomial centered at c. f(x) = x^2 cos x, n = 2, c = pi P2(x) =
Answers
The second-degree Taylor polynomial centered at c = π for the function f(x) = x² cos(x) is P₂(x) = -π² - 2π(x - π) + (-2 + π²)(x - π)² / 2
To find the nth Taylor polynomial centered at c for the function f(x) = x² cos(x), we need to find the values of the function and its derivatives at the point c and use them to construct the polynomial.
First, let's find the values of f(x) and its derivatives at the point c = π:
f(c) = c² cos(c) = π² cos(π) = π² * (-1) = -π²
f'(c) = (d/dx)(x² cos(x)) = 2x cos(x) - x² sin(x)
f'(c) = (d/dx)(π² cos(π)) = 2π cos(π) - π² sin(π) = 2π * (-1) - π² * 0 = -2π
f''(c) = (d^2/dx²)(x² cos(x)) = 2 cos(x) - 4x sin(x) - x² cos(x)
f''(c) = (d^2/dx²)(π² cos(π)) = 2 cos(π) - 4π sin(π) - π² cos(π) = 2 * (-1) - 4π * 0 - π² * (-1) = -2 + π²
Now, we can construct the Taylor polynomial of degree n = 2 centered at c = π:
P₂(x) = f(c) + f'(c)(x - c) + f''(c)(x - c)² / 2!
Substituting the values we found:
P₂(x) = -π² + (-2π)(x - π) + (-2 + π²)(x - π)² / 2!
Simplifying further:
P₂(x) = -π² - 2π(x - π) + (-2 + π²)(x - π)² / 2
The complete question is:
Find the nth Taylor polynomial centered at c. f(x) = x² cos x, n = 2, c = π P₂(x) = ?
To know more about second-degree:
https://brainly.com/question/369584
#SPJ4
in an informal survey of students, 20 have dogs, 15 have cats, and five have both. one has a pet squirrel. how many people have a pet dog or a pet cat?
Answers
The people have a pet dog or a pet cat would be 30.
What is Union and Intersection of a numbers?
The set of elements that are contained in either set X, set Y, or both sets X and Y is referred to as the union of two sets X and Y. The set of items that are a part of both sets X and Y is known as the intersection of two sets X and Y.
Given that:
In survey of students,
20 have dogs, 15 have cats, and 5 have both. 1 has a pet squirrel.
n(A)=Student who has dogs.
n(B)=Student who has cats.
and n(AUB)= Student who having both dogs and cats.
So,
n(A)=20
n(B)=15
n(AUB)=5
According to formula,
n(AUB)=n(A)+n(B)-n(A∩B)
i.e. n(A∩B)=n(A)+n(B)-n(AUB)
n(A∩B)=20+15-5
n(A∩B)=30
Hence, The people have a pet dog or a pet cat would be 30.
To know more about Intersection visit,
https://brainly.com/question/29129216
#SPJ4
The supply curve for product X is given by QXS = -340 + 10PX .
a. Find the inverse supply curve.
b. How much surplus do producers receive when Qx = 350? When Qx = 1,000?
Answers
a.The inverse supply curve is: PX = (QXS + 340)/10
b.when Qx = 350, the producer surplus is 4375, and when Qx = 1000, the producer surplus is 17000.
a. To find the inverse supply curve, we need to solve for PX in terms of QXS. Starting with the original equation:
QXS = -340 + 10PX
Add 340 to both sides:
QXS + 340 = 10PX
Divide both sides by 10:
(PX) = (QXS + 340)/10
So the inverse supply curve is:
PX = (QXS + 340)/10
b. To find the producer surplus, we need to calculate the area between the supply curve and the market price for a given quantity of X. The market price is equal to the supply curve equation. So for Qx = 350, we have:
QXS = -340 + 10PX
QXS = -340 + 10(35) = 10
Producer surplus = (35-10) x 350/2 = 4375
For Qx = 1000, we have:
QXS = -340 + 10PX
QXS = -340 + 10(100) = 660
Producer surplus = (100-66) x 1000/2 = 17000
Therefore, when Qx = 350, the producer surplus is 4375, and when Qx = 1000, the producer surplus is 17000.
Learn more about supply curve here:
https://brainly.com/question/31519928
#SPJ11
find the ordered pair that corresponds to the given pair of parametric equations and value of t. x = 4t + 5, y = -2t + 4; t = 2
The ordered pair is ...
Answers
The ordered pair that corresponds to the given pair of parametric equations and t = 2 is (13, 0).
We are given the pair of parametric equations:
x = 4t + 5
y = -2t + 4
and we need to find the ordered pair (x,y) when t = 2.
Substituting t = 2 into the equations, we get:
x = 4(2) + 5 = 13
y = -2(2) + 4 = 0
Therefore, the ordered pair that corresponds to the given pair of parametric equations and t = 2 is (13, 0).
To know more about parametric equations refer here:
https://brainly.com/question/28537985
#SPJ11
CAN YOU PLEASE HELP ME WITH THIS PROBLEM???
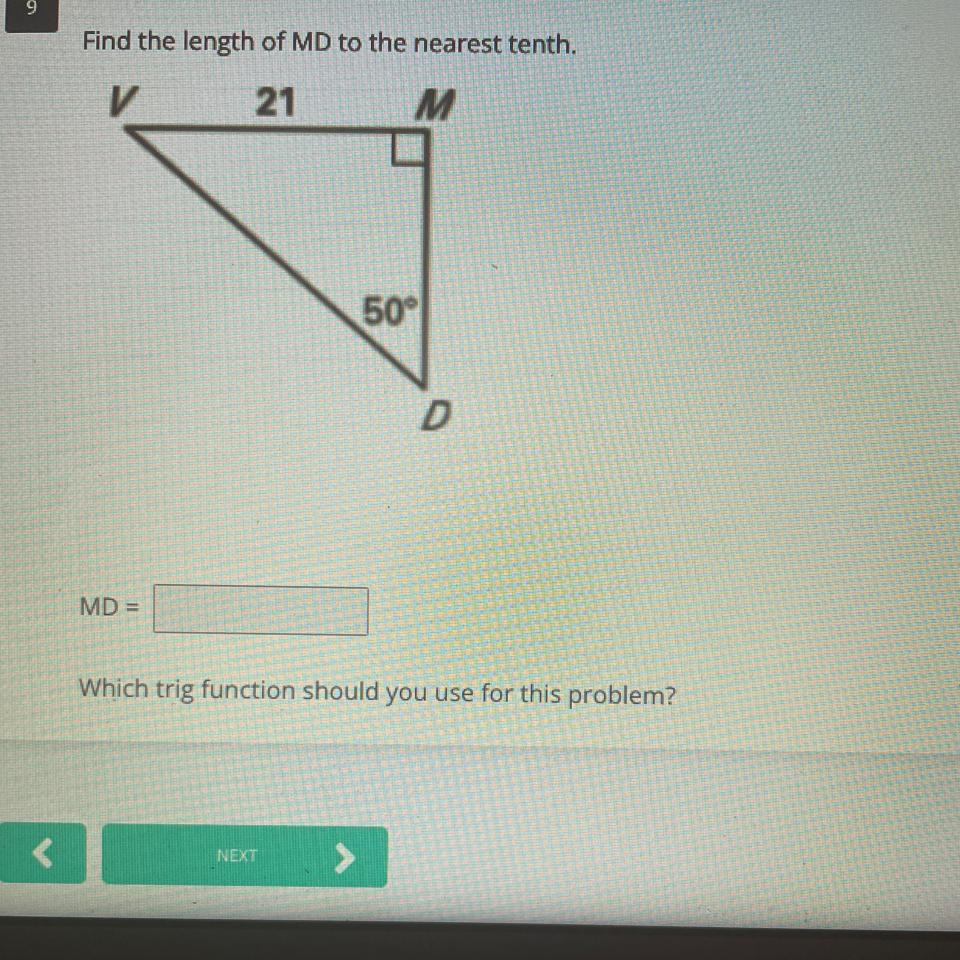
Answers
Answer:
Step-by-step explanation:
\(tan \ 50 =\dfrac{opposite \ side}{adjacent side}\\\\\\1.19=\dfrac{21}{MD}\\\\\\1.19*MD=21\\\\MD = \dfrac{21}{1.19}\\\\\\MD = 17.65\)
1. Find
A) 35
B) 47.5
C) 67.5
D95
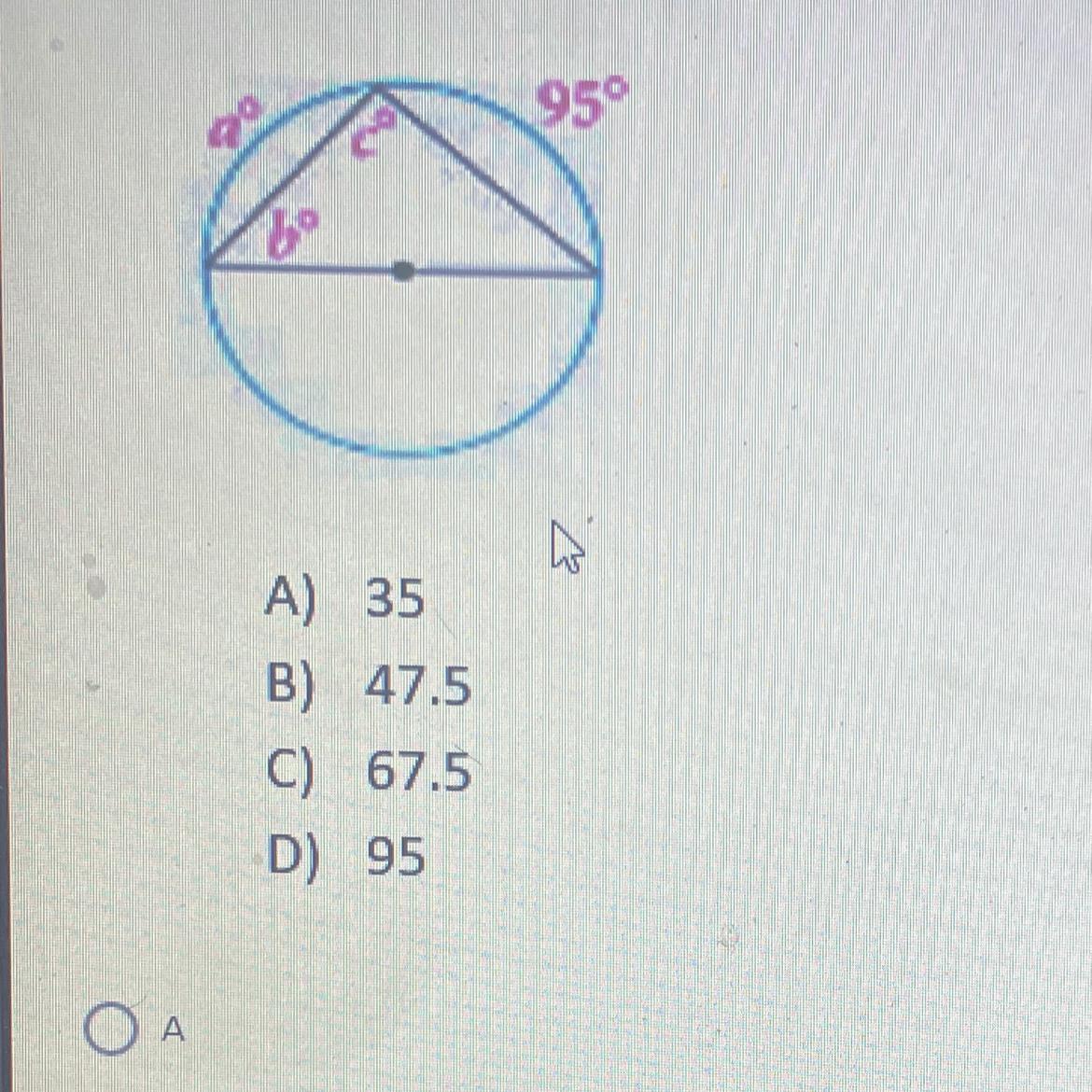
Answers
Answer:
find which one my guy im trying to get infinite awnseres srryyyyy
Step-by-step explanation:
-2x2 + 8x = 10 using the Quadratic Formula. Simplify if possible.
Answers
The required solutions are x = 2-i and x = 2+i to the given quadratic function.
What is a quadratic function?
The quadratic function is defined as a function containing the highest power of a variable is two.
We have been given that quadratic function as
-2x² + 8x - 10 = 0
Compare the given function to the standard quadratic function f(x) = ax² + b x + c.
We get a = -2, b = 8 and c = -10
Using the quadratic formula to solve the above quadratic function
\(x = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\)
\(x=\dfrac{-8\pm \sqrt{8^2-4\left(-2\right)\left(-10\right)}}{2\left(-2\right)}\)
\(x=\dfrac{-8\pm \:4i}{2\left(-2\right)}\)
\(x=\dfrac{-8+4i}{2\left(-2\right)},\:x=\dfrac{-8-4i}{2\left(-2\right)}\)
x = 2-i, x = 2+i
Thus, the required solutions are x = 2-i and x = 2+i to the given quadratic function.
Learn more about quadratic function here:
brainly.com/question/14083225
#SPJ1
In 2019 the average full time worker in the us spent 8.5 hours working each workday. this is an increase on the average of 8.1 hours per workday in 2014. what percent change for 2014 to 2019 round to the nearest tenth of the percent
Answers
The percentage increase in the working hours will be 4.9%.
How to illustrate the percentage?A percentage is a value or ratio that may be stated as a fraction of 100. If we need to calculate a percentage of a number, we should divide it's entirety and then multiply it by 100.
Since in 2019 the average full time worker in the us spent 8.5 hours working each workday. this is an increase on the average of 8.1 hours per workday in 2014.
The percentage increase will be:
= (8.5 - 8.1) / 8.1 × 100
= 0.4 / 8.1 × 100
= 4.9%
Learn more about percentages on
brainly.com/question/24877689
#SPJ1
Decompose v into two vectors, v1 and v2, where v1 is parallel to w and v2 is orthogonal to w.
v = i - j, w = -i + 2j
Answers
The two components v₁ = (2/5)i - (4/5)j (parallel to w), v₂ = (3/5)i - (9/5)j (orthogonal to w).
To decompose vector v into two components, one parallel to vector w and the other orthogonal to vector w, we can use the concepts of projection and cross product.
Let's start by finding the component of v that is parallel to w, denoted as v₁. The parallel component can be calculated using the projection formula:
v₁ = ((v · w) / ||w||²) * w
where "·" represents the dot product and "||w||²" denotes the squared magnitude of w.
Calculating the dot product of v and w:
v · w = (i - j) · (-i + 2j)
= -i² + 2(i · j) - j²
= -1 + 0 - 1
= -2
Calculating the squared magnitude of w:
||w||² = (-i + 2j) · (-i + 2j)
= i² - 2(i · j) + 4j²
= 1 - 0 + 4
= 5
Substituting these values into the formula for v₁:
v₁ = ((-2) / 5) * (-i + 2j)
= (2/5)i - (4/5)j
Next, we can find the component of v that is orthogonal to w, denoted as v₂. This can be obtained by subtracting the parallel component (v₁) from v:
v₂ = v - v₁
= i - j - (2/5)i + (4/5)j
= (3/5)i - (9/5)j
Therefore, we have decomposed vector v into two components:
v₁ = (2/5)i - (4/5)j (parallel to w)
v₂ = (3/5)i - (9/5)j (orthogonal to w)
Learn more about orthogonal here
https://brainly.com/question/30772550
#SPJ11
Explain how to write a mixed number as a division expression. Drag the words to the appropriate positions. Not all the words will be used.
fraction added to
numerator denominator quotient divisor remainder
First, write the mixed number as an improper
fraction
. Then, use the
as the dividend and the
as the
in the division expression
Answers
The mixed number 2 1/3 can be written as the division expression 7/3 ÷ 3, which simplifies to 7/9, with a remainder of 1/3.
To write a mixed number as a division expression, the following steps must be followed:
Step 1: Convert the mixed number to an improper fraction.
Step 2: Use the denominator of the improper fraction as the divisor and the numerator as the dividend in the division expression.
Step 3: Express the division expression in the simplified form by performing the division and identifying the quotient and the remainder (if any).Here's an example:
Write the mixed number 2 1/3 as a division expression.Step 1: Convert the mixed number to an improper fraction.2 1/3 = (2 × 3 + 1)/3 = 7/3Step 2: Use the denominator of the improper fraction as the divisor and the numerator as the dividend in the division expression.7/3 ÷ 3
Step 3: Express the division expression in the simplified form by performing the division and identifying the quotient and the remainder (if any).7/3 ÷ 3 = 7/3 × 1/3 = 7/9, with a remainder of 1/3.
The mixed number 2 1/3 can be written as the division expression 7/3 ÷ 3, which simplifies to 7/9, with a remainder of 1/3.
Learn more about division here:
https://brainly.com/question/2273245
#SPJ11
Help!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
523
Step-by-step explanation:
Move the decimal so there is one non-zero digit to the left of the decimal point. The number of decimal places you move will be the exponent on the 10.
5.23 x \(10^{2}\)
Scientific Notation: 5.23 x \(10^{2}\)
Expanded Form: 523
good luck, hope this helps :)
what is the meaning of interval [a,b]
Answers
Answer:
Step-by-step explanation:
interval in mathematics stands for a set of real numbers,
denoted by [a,b] where a and b are the starting and ending real numbers both inclusive respectively.
thus, interval [a,b] is the set of real numbers starting from a to b both are real numbers and are included.
Describe the translation from triangle ABC (red) to triangle A'B'C' (blue) in words. Use words like up, down, left, right. *

Answers
Answer:
3 up and 5 to the left
Step-by-step explanation:
Just focus on one point. I focused on A and then saw where A' was and then matched it up.
Someone please help me!!!

Answers
Answer: Answer is B
Step-by-step explanation:
Remeber that the shorter a container is doesn't mean it has less mass or volume. the width can mean it holds more. If the radius is twice as big that can mean the contents is more and your getting a better deal. hOpe this will help.
Y=5575•(0.65)^ta. What is the initial value? b. What is the decay factor?
Answers
a) Initial Value = 5575
Decay factor = 0.35
Explanation:The given expression is:
\(Y\text{ = 5575}\times(0.65)^t\)a) What is the initial value
The initial value of Y will take place when t = 0
Substituting t = 0 into the given equation:
\(Y\text{ = 5575}\times(0.65)^0\)\(Y=\text{ 5575 }\times\text{ 1 = 5575}\)The initial value is Y = 5575b) What is the decay factor
The value of a substance due to an exponential decay is given by the general expression:
\(Y=A(1-r)^t\)Where A = original/Initial value, and r = decay rate
Comparing the above equation with the given equation shown below:
\(Y=5575(0.65)^t\)It is clear from the comparison of both equations that A = 5575 and :
1 - r = 0.65Solving for r:r = 1 - 0.65r = 0.35The decay factor is 0.35Define the following in your own words. Please do not copy and paste of the internet. Thank you in advance
Perpendicular bisector
Cylinder
Plane
Regular Polygon
Answers
Answer:
Perpendicular bisector - A line that bisects another line into two equal halves so that four right angles are created.
Cylinder - A 3D solid with circles as its bases.
Plane - A flat, 2D surface that extends infinitely.
Regular Polygon - A polygon where all angles and all sides are equal (ex. square, pentagon, triangle).
The following is a set of data from a sample of
n=5.
4 −9 −4 4 6
a. Compute the mean, median, and mode.
b. Compute the range, variance, standard deviation, and coefficient of variation.
c. Compute the Z scores. Are there any outliers?
d. Describe the shape of the data set.
Answers
a. The mean is -0.6, the median is 4, and there is no mode in the data set.
b. The range is 15, the variance is 35.2, the standard deviation is approximately 5.93, and the coefficient of variation is approximately -0.988.
c. The Z-scores for the data set are -0.68, -1.69, -0.68, -0.68, and 1.37. There are no outliers as none of the Z-scores exceed the threshold of ±3.
d. The shape of the data set is skewed to the left, indicating a negative skewness.
a. To calculate the mean, we sum up all the values and divide by the sample size:
Mean = (4 - 9 - 4 + 4 + 6) / 5 = -0.6
The median is the middle value when the data is arranged in ascending order:
Median = 4
The mode is the value that appears most frequently, but in this data set, none of the values are repeated, so there is no mode.
b. The range is calculated by finding the difference between the maximum and minimum values:
Range = Maximum value - Minimum value = 6 - (-9) = 15
The variance measures the average squared deviation from the mean:
Variance = ((4 - (-0.6))^2 + (-9 - (-0.6))^2 + (-4 - (-0.6))^2 + (4 - (-0.6))^2 + (6 - (-0.6))^2) / (5 - 1) = 35.2
The standard deviation is the square root of the variance:
Standard Deviation ≈ √35.2 ≈ 5.93
The coefficient of variation is the standard deviation divided by the mean, expressed as a percentage:
Coefficient of Variation ≈ (5.93 / 0.6) × 100 ≈ -0.988
c. The Z-score measures how many standard deviations a data point is away from the mean. To calculate the Z-scores, we subtract the mean from each data point and divide by the standard deviation:
Z1 = (4 - (-0.6)) / 5.93 ≈ -0.68
Z2 = (-9 - (-0.6)) / 5.93 ≈ -1.69
Z3 = (-4 - (-0.6)) / 5.93 ≈ -0.68
Z4 = (4 - (-0.6)) / 5.93 ≈ -0.68
Z5 = (6 - (-0.6)) / 5.93 ≈ 1.37
Since none of the Z-scores exceed the threshold of ±3, there are no outliers in the data set.
d. The shape of the data set can be determined by analyzing the skewness. A negative skewness indicates that the data is skewed to the left, which means that the tail of the distribution extends towards the lower values. In this case, the negative skewness suggests that the data set is skewed to the left.
To know more about mean , visit
https://brainly.com/question/1136789
#SPJ11
Find the HCF of
x^2 y and y^2
Answers
The highest common factor is \(\boxed{y}\).
A political scientist was interested in studying america's voting habits. So, he decided to make a least squares regression equation to predict the percentage of people in a state that would vote for obama in 2012 based on the percentage of people in a state that voted for obama in 2008. The least squares equation is y-hat = -4. 599 +1. 04x. In the state of wyoming, 32. 54% voted for obama in 2008; whereas, 27. 82% voted for him in 2012. What is the value of the residual?.
Answers
The residual in this case is 4.72%, which is calculated by taking the difference between the predicted value (32.54%) and the actual value (27.82%).
The political scientist's least squares regression equation predicted that 32.54% of people in Wyoming would vote for Obama in 2012. However, the actual percentage of people who voted for Obama in Wyoming in 2012 was 27.82%, which was lower than the predicted value. This difference between the predicted and actual value is the residual, which in this case is 4.72%. This suggests that the least squares equation was not very accurate in predicting the voting habits in Wyoming for the 2012 election.
Learn more about Elections: https://brainly.com/question/3710013
#SPJ4
For the past week, a company's common stock closed with the following prices: $61.5, $62, $61.25, $60.875, and $61.5. What was the price range?
a $1.250
b $1.750
c $1.125
d $1.875
Answers
The price range for the past week's common stock is $1.125.
To calculate the price range, we need to find the difference between the highest and lowest prices. The highest price is $62 and the lowest price is $60.875. So, the difference between them is:
$62 - $60.875 = $1.125
Therefore, the price range for the past week's common stock is $1.125.
This information can be useful for investors who are monitoring the performance of the company's stock over time.
For more questions like Stock click the link below:
https://brainly.com/question/31476517
#SPJ11
The graph of a sinusoidal function intersects its midline at (0,−3)and then has a maximum point at (2,-1.5). Write the formula of the function, where x is entered in radians. f(x)= Please answer fast
Answers
The sinusoidal function that represents the graph is equal to y = 1.5 · cos (2π · t/8) - 3.
How to derive a sinusoidal function
In this question we must derive a sinusoidal function based on two given points. Sinusoidal functions are periodic functions that uses trigonometric functions and have the following form:
y = A · cos (2π · x/T) + B (1)
Where:
A - AmplitudeT - Period B - Vertical midpointThe horizontal distance between the midline and the maximum point is equal to a quarter of the period. Hence,
T = 4 · (2 - 0)
T = 8
The vertical midpoint and amplitude of the sinusoidal function are now calculated:
Vertical midpoint
B = - 3
Amplitude
A = - 1.5 - (- 3)
A = 1.5
Then, the sinusoidal function that represents the graph is equal to y = 1.5 · cos (2π · t/8) - 3.
To learn more on sinusoidal functions: https://brainly.com/question/12060967
#SPJ1
Complete the identity. cos (2pi - x) =?
Please I need help this test is due! :/
I need help with number 5

Answers
the identity is:
cos(2π - x) = cos(x)
Using the angle sum identity for cosine, we have:
cos(2π - x) = cos(2π)cos(x) + sin(2π)sin(x)
Since cos(2π) = 1 and sin(2π) = 0, this simplifies to
cos(2π - x) = cos(x)
what is cosine?The ratio between the adjacent side and the hypotenuse is known as the cosine function (or cos function) in triangles. One of the three fundamental trigonometric functions, cosine is the complement of sine (co+sine) and one of the three main trigonometric functions.
The ratio of the neighboring side's length to the longest side, or hypotenuse, in a right triangle is known as the cosine. Let's say that the hypotenuse of a triangle ABC is written as AB, and the angle between the hypotenuse and base is written as.
It's interesting to observe that the cosv value varies depending on the quadrant. As observed , cos 0°, 30°, etc. have positive values while cos 120°, 150°, and 180° have negative values. Cos will have a good value in the first and fourth quadrants.
from the question:
Using the angle sum identity for cosine, we have:
cos(2π - x) = cos(2π)cos(x) + sin(2π)sin(x)
Since cos(2π) = 1 and sin(2π) = 0, this simplifies to:
cos(2π - x) = cos(x)
Therefore, the identity is:
cos(2π - x) = cos(x)
to learn more about cosine visit
https://brainly.com/question/29114352
#SPJ1
f(x1, x2) 421 +222 3x² +213 5x11² (√₁+√₂)² 10ln(₁) (x₁+x₂)(x² + x3) min(3r1, 10√2) max{5x1,2r2} MP1(x1, x₂) MP2(X1, X₂) TRS(x1, x₂) Output (2,4)
Answers
The given mathematical expression is evaluated for the input values (2, 4). The result of the expression is calculated using various operations such as addition, multiplication, square root, natural logarithm, minimum, maximum, and function composition.
The expression f(x1, x2) involves several mathematical operations. Let's evaluate each part of the expression step by step:
1. The first term is 421 + 222, which equals 643.
2. The second term is 3x² + 213. Plugging in x1 = 2 and x2 = 4, we get 3(2)² + 213 = 3(4) + 213 = 12 + 213 = 225.
3. The third term is 5x11². Substituting x1 = 2 and x2 = 4, we have 5(2)(11)² = 5(2)(121) = 1210.
4. The fourth term is (√₁+√₂)². Replacing x1 = 2 and x2 = 4, we obtain (√2 + √4)² = (1 + 2)² = 3² = 9.
5. The fifth term is 10ln(₁). Plugging in x1 = 2, we have 10ln(2) = 10 * 0.69314718 ≈ 6.9314718.
6. The sixth term is (x₁+x₂)(x² + x3). Substituting x1 = 2 and x2 = 4, we get (2 + 4)(2² + 4³) = 6(4 + 64) = 6(68) = 408.
7. The seventh term is min(3r1, 10√2). As we don't have the value of r1, we cannot determine the minimum between 3r1 and 10√2.
8. The eighth term is max{5x1,2r2}. Since we don't know the value of r2, we cannot find the maximum between 5x1 and 2r2.
9. Finally, we have MP1(x1, x2), MP2(X1, X2), and TRS(x1, x2), which are not defined or given.
Considering the given expression, the evaluated terms for the input values (2, 4) are as follows:
- 421 + 222 = 643
- 3x² + 213 = 225
- 5x11² = 1210
- (√₁+√₂)² = 9
- 10ln(₁) ≈ 6.9314718
- (x₁+x₂)(x² + x3) = 408
The terms involving min() and max() cannot be calculated without knowing the values of r1 and r2, respectively. Additionally, MP1(x1, x2), MP2(X1, X2), and TRS(x1, x2) are not defined.
To learn more about logarithm click here: brainly.com/question/30226560
#SPJ11
find the critical value that corresponds to the given confidence level.
Answers
The critical value that corresponds to a 90% confidence level is 1.645.
When we are given a confidence level, we can use a confidence interval to calculate the margin of error, and with that we can find the critical value. The critical value is the value that represents the number of standard deviations we need to go from the mean to capture a certain proportion of the distribution.
For example, for a 95% confidence level, we want to capture 95% of the distribution, so we need to go 1.96 standard deviations from the mean.To find the critical value that corresponds to a given confidence level, we need to use a table of critical values for the standard normal distribution. This table tells us how many standard deviations we need to go from the mean to capture a certain proportion of the distribution.
For example, the critical value for a 95% confidence level is 1.96, while the critical value for a 99% confidence level is 2.58. So, if we are given a confidence level of 90%, we need to find the critical value that corresponds to capturing 90% of the distribution.Using the table of critical values, we find that the critical value for a 90% confidence level is 1.645.
for such more question on critical value
https://brainly.com/question/15970126
#SPJ11
how do I factor trinomials of a form ax^2+bx+c when a=1
In one paragraph
Answers
Answer:
Trinomials in the form \(x^2+bx+c\) can often be factored as the product of two binomials.Step-by-step explanation:
As we know that a polynomial with three terms is said to be a trinomial.
Considering the trinomial of a form
\(ax^2+bx+c\)
As
a = 1
so
\(x^2+bx+c\)
Trinomials in the form \(x^2+bx+c\) can often be factored as the product of two binomials.For example,
\(x^2+7x+10\)
\(=\left(x^2+2x\right)+\left(5x+10\right)\)
\(=x\left(x+2\right)+5\left(x+2\right)\)
\(\mathrm{Factor\:out\:common\:term\:}x+2\)
\(=\left(x+2\right)\left(x+5\right)\)
Therefore, Trinomials in the form \(x^2+bx+c\) can often be factored as the product of two binomials.
Part 1
A scale drawing of a rectangular park is 5 inches wide and 7 inches long. The actual park is 250 yards long. How many yards is the length of the park?
Part 2
Use your answer from part 1 to solve the following problem.
A scale drawing of a rectangular park is 5 inches wide and 7 inches long. The actual park is 250 yards long. What is the area of the actual park?
someone please anwser ASAP its due today
Answers
Answer:
Part 1
If the actual park is 250 yards LONG, I think it means that its LENGTH is also 250 yards
Part 2
It's a proportion:
5=x
7=250
5*250:7=178.6 yards
The area is 178.6 yards wide and 250 yards long
Step-by-step explanation:
easy algebra question below first correct answer gets brainliest

Answers
Answer:
3
Step-by-step explanation:
Easy pythagorean theorum question.
The law states that "A squared plus B squared, equals C squared."
A and B are the two sides that border the 90 degree mark.
C is the hypotenuse or the longest side/diagonal.
Since we know C and A (I chose to use A because why not) we can fill in the equation with what we know
2^2 + ?^2 = \(\sqrt{13^{2} }\)
So
4 + ?^2 = \(\sqrt{13^{2} }\)
Since the 13 is already squared in side of a root, it stays as 13
4 + x^2 = 13
4 - 4 + x^2 = 13 - 4
x^2 = 9
x^2 root = root of 9
x = 3
The missing side is 3.
Or you could use an online calculator xD
Find the value of X
PLEASE HELP ASAP!!!!!

Answers
Answer:
-10
Step-by-step explanation:
the upper right is the same (105°), therefore the left 75°
now you have 180 = 75 + x + 115
therefore: -10
An inclined plane makes an angle of theta with the horizontal.