find the midpoint coordinate between 6 ,2 and 9, 4
Answers
Related Questions
Two window washers are on a
skyscraper. One is at a height of
700 feet and the other is at a height:
of 300 feet.
Write an equation and
find the solution for the difference in
the window washer's heights.
300 1691
705120
Answers
Answer: 400 ft
Step-by-step explanation:
o=Window Washer one. t=Window Washer two. d=difference
o-t=d
700-300=d
d=400 ft
At a baseball game, a vender sold a combined total of 191 sodas and hot dogs. The number of hot dogs sold was 47 less than the number of sodas sold. Find the number of sodas sold and the number of hot dogs sold.
Answers
The number of sodas sold at the baseball game was 119, while the number of hot dogs sold was 72.
Let's assume the number of sodas sold as 'x' and the number of hot dogs sold as 'y'.
According to the problem, the total number of sodas and hot dogs sold is 191, so we can write the equation:
x + y = 191 ...(1)
The problem also states that the number of hot dogs sold was 47 less than the number of sodas sold. Mathematically, we can express this as:
y = x - 47 ...(2)
To find the values of x and y, we can solve the system of equations (1) and (2). Substituting equation (2) into equation (1), we have:
x + (x - 47) = 191
Simplifying the equation:
2x - 47 = 191
2x = 191 + 47
2x = 238
Dividing both sides by 2:
x = 238/2
x = 119
Substituting the value of x back into equation (2):
y = 119 - 47
y = 72
As a result, the total amount of sodas sold is 119, and the total amount of hot dogs sold is 72.
For more such questions on number, click on:
https://brainly.com/question/24644930
#SPJ8
5.5 is what percent of 6.875. Could you explain how to get the answer.
Answers
Based on the information given in the exercise, you can identify that the number that represents the 100% is the following:
\(6.875\)Then, let be "x" the percent asked in the exercise.
Using the information given, you can set up the following proportion:
\(\frac{100}{6.875}=\frac{x}{5.5}\)Now you must solve for "x" in order to find its value. To do this, you can use this procedure:
1. Multiply both sides of the equation by 5.5:
\(\begin{gathered} (5.5)(\frac{100}{6.875})=(\frac{x}{5.5})(5.5) \\ \\ \frac{550}{6.875}=x \end{gathered}\)2. Divide the numerator by the denominator:
\(x=80\)The answer is: 80%
What is the range of the function? f(x)=3^x−1−2
Answers
The range of the equation f(x) = 3ˣ ⁻ ¹ - 2 is y > -2
Calculating the range of the equation?From the question, we have the following parameters that can be used in our computation:
f(x) = 3ˣ ⁻ ¹ - 2
The above equation is an exponential function
The rule of an exponential function is that
The domain is the set of all real numbersHowever, the range is always greater than the constant termIn this case, it is -2
So, the range is y > -2
Read more about range at
brainly.com/question/27910766
#SPJ1
what’s the quotient of -15b^5+18b^3/3b
Answers
This is the quotient of (-15b^5 + 18b^3) divided by 3b. The expression simplifies to -5b^4 + 6b^2.
To find the quotient of the expression (-15b^5 + 18b^3) divided by 3b, we can perform the division by simplifying each term separately.
First, let's divide -15b^5 by 3b:
(-15b^5) / (3b) = -15/3 * b^5/b = -5 * b^(5-1) = -5b^4
Next, let's divide 18b^3 by 3b:
(18b^3) / (3b) = 18/3 * b^3/b = 6 * b^(3-1) = 6b^2
Now, we have simplified each term individually. The resulting expression is:
-5b^4 + 6b^2
This is the quotient of (-15b^5 + 18b^3) divided by 3b. The expression simplifies to -5b^4 + 6b^2.
for such more question on quotient
https://brainly.com/question/25289437
#SPJ8
A gym asks its customers about the kinds of athletic activities they do outside of the gym and records the results in the
table below.

Answers
The probability that a randomly selected part-time student has a gym membership is approximately 0.2667 or 26.67%.
Here, we have to solve the question:
To calculate the probability that a randomly selected part-time student has a gym membership, we need to use conditional probability. Specifically, we need to use Bayes' theorem
P(Gym Membership | Part-Time) = P(Part-Time | Gym Membership) * P(Gym Membership) / P(Part-Time)
Where:
P(Gym Membership | Part-Time) is the probability that a student has a gym membership given that they are part-time.
P(Part-Time | Gym Membership) is the probability that a student is part-time given that they have a gym membership.
P(Gym Membership) is the overall probability of a student having a gym membership (regardless of whether they are full-time or part-time).
P(Part-Time) is the overall probability of a student being part-time (regardless of whether they have a gym membership).
Let's start by filling in the values we know from the table:
P(Part-Time) = (40 + 25) / 155 = 0.5484
P(Gym Membership) = (30 + 25) / 155 = 0.3226
P(Part-Time | Gym Membership) = 25 / (30 + 25) = 0.4545
To find P(Gym Membership | Part-Time), we need to calculate P(Part-Time and Gym Membership). We can use the formula:
P(Part-Time and Gym Membership) = P(Part-Time | Gym Membership) * P(Gym Membership)
Plugging in the values we know, we get:
P(Part-Time and Gym Membership) = 0.4545 * 0.3226 = 0.1463
Now we can use this value, along with P(Part-Time) and P(Gym Membership), to calculate P(Gym Membership | Part-Time):
P(Gym Membership | Part-Time) = 0.1463 / 0.5484 ≈ 0.2667
Therefore, the probability that a randomly selected part-time student has a gym membership is approximately 0.2667 or 26.67%.
To know more about probability visit :-
brainly.com/question/13604758
#SPJ1
complete question:
a group of 155 students at a private university were asked if they are full-time or part-time and if they have gym memberships. the results are shown in the table below. given that a randomly selected survey participant is part-time, what is the probability that this student has a gym membership?
The slope of the tangent line to the curve y= 3/x
at the point 5, 3/5 is-
The equation of this tangent line can be written in the form y = mx + b
where:
m is:
b is:

Answers
The tangent line at that point is:
y = (-3/25)*x + 6/5
so m = -3/25, and b = 6/5
How to find the slope of the tangent line?To find the slope at that point, we need to evaluate the derivative at that point.
y = 3/x
The derivative is:
y' = -3/x²
When x = 5, we have:
y' = -3/5² = -3/25
So that is the slope, m.
Now let's find the line.
The line must pass trhough the point (5, 3/5), then:
3/5 = (-3/25)*5 + b
3/5 = -3/5 + b
3/5 + 3/5 = b
6/5 = b
The equation of the line is:
y = (-3/25)*x + 6/5
Learn more about the tangent line:
https://brainly.com/question/30162650
#SPJ1
Una cuenta de ahorros tiene $20,000. Se le aplica un interés del 2.5% anual, compuesto por trimestre.
Debe usar A = P ( 1+ (r/n) )nt
Calcular la cantidad de dinero que habrá acumulado en 15 años.
Diga cuántos años habría que esperar para alcanzar el doble de dicha cantidad inicial.
Answers
Answer: A = 29,065.888
t = 27.81244 ≈ 27.81
Step-by-step explanation:
Principal P = 20,000
rate = 2.5 % = 0.025
t = 15 years
n = 4 (Compuestro trimestral)
Lo que sabemos
A = P ( 1 + r/n)∧nt
A = 20,000 ( 1 + 0.025/4 ) ∧4*15
A = 20,000 × 1.4532944
A = 29,065.888
Cantidad de dinero acumulada en 15 años $ 29,065.888
A = 2 × 20,000 = 40,000
40,000 = 20,000 (1+ 0.025/4)∧4t
40,000/20,000 = (1.00625)∧4t
Sacamos el logaritmo ha ambos lados de la ecuación:
ln (2) = ln (1.00625)∧4t
ln (2) = 4t × ln (1.00625)
t = 27.81244 ≈ 27.81
28 años habría que esperar para alcanzar el doble de dicha cantidad inicial.
Which function has real zeros at x = 3 and x = 7?
f(x) = x2 + 4x - 21
O f(x) = x2 - 4x - 21
O f(x) = x2 – 10x + 21
O f(x) = x2 – 10x - 21
Answers
all of them will give u zero
but not all of them
in the first one only if you equate x to be 3 that is when it will give u zero
for the second one is only when u equate x to be seven that's when it will be equal to zero
the same thing for the rest!
There are 26 boys and 20 girls in a class.
The boys and the girls have some counters.
The mean number of counters that the boys have is 28.
The mean number of counters that the girls have is 19.
Work out the mean number of counters the 46 children have.
Answers
Computing the total number of counters in the class as 1,108, the mean number of counters that the 46 children have is 24.
What is the mean?The mean refers to the average value.
The average is the quotient of the total value divided by the number of items in the data set.
The number of boys in the class = 26
The number of girls in the class = 20
The total number of boys and girls in the class = 46
The mean number of counters that the boys have = 28
The total number of counters that the boys have = 728 (28 x 26)
The mean number of counters that the girls have =19
The total number of counters that the girls have = 380 (19 x 20)
The total number of counters that the class has = 1,108 (728 + 380)
The average or mean number of counters in the class = 24 (1,108 ÷ 46)
Learn more about the average at https://brainly.com/question/130657.
#SPJ1
Translate to an equation please.
four less than thirteen times a number is equal to that number added to eight
Answers
Hi
let call "a number" X.
then we have: 4-13X = X + 8 ..
13x-x = 8+ 4
12x= 12
X= 1
Find the measure of angle AEB

Answers
Answer:
∠ AEB = 114°
Step-by-step explanation:
the chord- chord angle AEB is half the sum of the measures of the arcs intercepted by the angle and its vertical angle , that is
∠ AEB = \(\frac{1}{2}\) (AB + CD) = \(\frac{1}{2}\) (140 + 88)° = \(\frac{1}{2}\) × 228° = 114°
16) Solve for side AB.
AB-
Round your answer to the nearest hundredth.
A) 5.45
B) 6.45
C) 7.45

Answers
Answer:
AB= 7.45
Anwer C)
Step-by-step explanation:
Cos (angle) = Nearest side / Huypothenuse
Cos(20) = 7 / AB
Cos(20) * AB = (7 /AB) * AB
Cos (20) * AB = 7
(Cos(20) *AB) / Cos(20) = 7 / Cos(20)
AB = 7 / cos(20)
AB= 7.45
In order to find the hypotenuse, we can use the trigonometric function “cosine”,
since.
Cosine =
Adjacent side (which is 7) / hypotenuse
Cos(50) = 7 / AB
AB = 7 / Cos(50)
AB = 10.89006678802289
AB ≈ 10.89
Have a good day ^^
Determine the equation (picture).

Answers
The line perpendicular to the equation and has the same y-intercept with another is y = - 4 / 3 x + 4.
How to find equation of a line?The equation of a line can be describe as follows:
y = mx + b
where
m = slopeb = y-interceptTherefore, lines that a perpendicular follows the rule below:
m₁m₂ = -1
Hence,
y + 6 = 3 / 4 (x - 2)
y + 6 = 3 / 4 x - 6 / 4
y = 3 / 4 x - 6 / 4 - 6
y = 3 / 4 x - 30 / 4
y = 3 / 4 x - 15 / 2
Hence,
3 / 4 m₂ = -1
m₂ = - 4 / 3
Therefore,
slope of the line is - 4 / 3
Let's find the y-intercept of the second line
4x + 5y -20 = 0
5y = -4x + 20
y = -4 / 5 x + 4
y-intercept = 4
Therefore, the line perpendicular to the equation and has the same y-intercept with another is y = - 4 / 3 x + 4.
learn more on equation here: https://brainly.com/question/14005330
#SPJ1
i dont know answer please im in summer school

Answers
The centre and the radius of the circle is (-7, -1) and 6 units
Equation of a circleThe equation of the circle in standard from is expressed as:
x^2+y^2+2gx+2fy+C = 0
where;
(-g, -f) is the centre
r= √g²+f²-C
Given the equation below
x^2+y^2+14x+2y+14 = 0
2g = 14
g = 7
2f = 2
f =1
Hence the centre of the circle is (-7, -1)
Radius = √49+1-14
Radius = √36 = 6 units
Hence the centre and the radius of the circle is (-7, -1) and 6 units
Learn more on equation of a circle here: https://brainly.com/question/1506955
#SPJ1
Which transformation is needed to be used on x^2, to get the graph of f(x) = 2x2 - 12x + 22?
Select one:
O a. Shift right by 3 units, stretch vertically by a factor 2 and then shift upward by 13 units
O b. Shift left by 3 units, stretch vertically by a factor 2 and then shift upward by 4 units
O c. Shift right by 3 units, stretch vertically by a factor 2 and then shift upward by 4 units
O d. Shift right by 3 units and shift upwards by 4 units
Please I need help
Answers
Answer: A
Step-by-step explanation:
The required transformation is Shift left by 3 units, stretch vertically by a factor 2 and then shift upward by 4 units. Hence option B is correct.
What is graph?The graph is a demonstration of curves which gives the relationship between x and y axis.
Since, both curve of x² and 2x² - 12x + 22 is in the graph.
Now, the steps of transformation of x² into 2x² - 12x + 22 is as follows.
1) Shift left by 3 units.
2) Stretch vertically by a factor 2.
3) Shift upward by 4 units
Thus, the required result will be seen graph.
Learn more about graphs here:
brainly.com/question/16608196
#SPJ2

Factorise x2 - 2x - 3
Answers
x= -1,3
This is the answer
The factorization of x² - 2x - 3 is (x+1)(x-3).
The given quadratic equation is,
x² - 2x - 3
The definition of a quadratic as a second-degree polynomial equation demands that at least one squared term must be included. It also goes by the name quadratic equations. The quadratic equation has the following generic form:
ax² + bx + c = 0
Hence to factorize we can write the given quadratic equation as,
⇒ x² - 3x + x - 3
⇒ x(x-3) + (x - 3)
⇒ (x+1)(x-3)
Hence,
x² - 2x - 3 = (x+1)(x-3)
To learn more about quadratic equation visit:
https://brainly.com/question/30098550
#SPJ6
Ahmad is saying that │ – 4│= – 4. Do you agree with him or not Justify ur reasoning
Answers
Answer:
No
Absolute Value is the Distance From Zero, and distance is always NON-negative.
Step-by-step explanation:
Answer: No
Step-by-step explanation: │ – 4│= 4 because it is four spaces away from zero <---,----,----,--->
-4 0 4
Enter the number that belongs in the green box
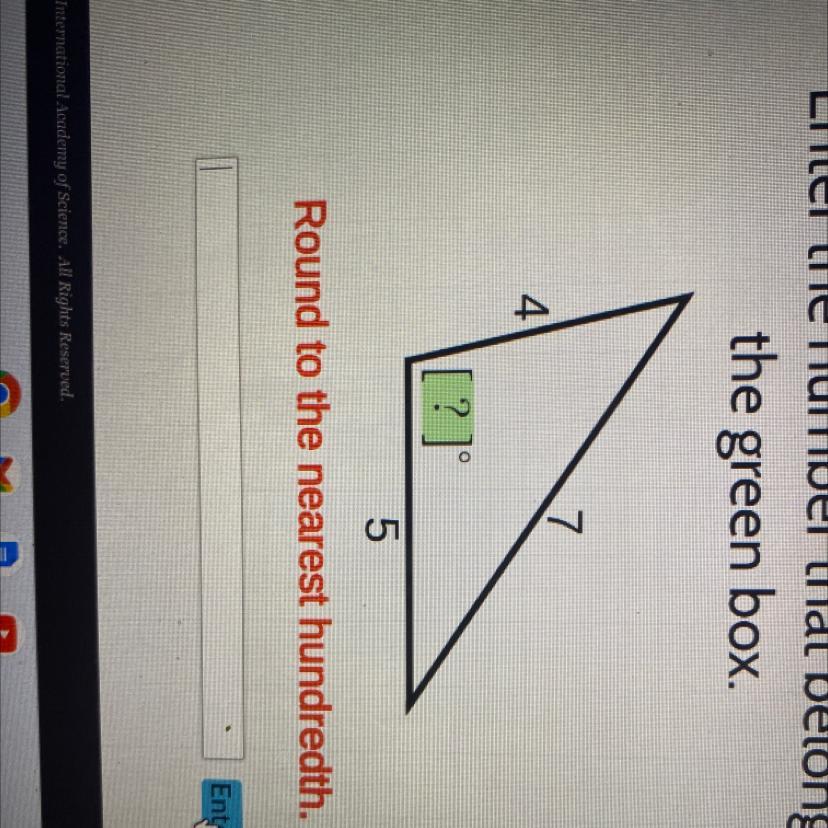
Answers
The angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
To find the measure of the angle between the sides measuring 4 and 5 in an obtuse triangle with side lengths 4, 5, and 7, we can use the Law of Cosines. The Law of Cosines states that in a triangle with side lengths a, b, and c, and an angle opposite to side c, the following equation holds:
\(c^2 = a^2 + b^2 - 2ab*cos(C)\)
In this case, we have side lengths a = 4, b = 5, and c = 7. We want to find the angle C, which is opposite to side c. Substituting these values into the Law of Cosines, we get:
\(7^2 = 4^2 + 5^2\)- 2(4)(5)*cos(C)
49 = 16 + 25 - 40*cos(C)
49 = 41 - 40*cos(C)
40*cos(C) = 41 - 49
40*cos(C) = -8
cos(C) = -8/40
cos(C) = -0.2
To find the measure of angle C, we can take the inverse cosine (arccos) of -0.2:
C = arccos(-0.2)
Using a calculator, we find that C ≈ 101.54 degrees.
Therefore, the measure of the angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
For more such information on: angle
https://brainly.com/question/25716982
#SPJ8
What is the solution to 3+x=x+3
Answers
Answer:
all real numbers
Step-by-step explanation:
if you subtract x from both sides, you get x=x. This is true for basically any number
6. stand by me [14 points] what is the expected number of pairs of people who are standing next to each other in line and in the same grup
Answers
The expected number of pairs of people who are standing next to each other in line and in the same group is ( 2n ) ! / 2^n * n! .
Given :
stand by me [14 points] what is the expected number of pairs of people who are standing next to each other in line and in the same group .
we know that ,
Number of pairs is determined by using the concept combinations of binomial distribution .
= ( 2n ) ! / 2^n * n !
here we represent * has . for multiplication to reduce the complexity .
= ( 2n ) ! / 2^n . n!
Learn more about the number here:
https://brainly.com/question/17429689
#SPJ4
Please help thank uuuuu

Answers
Answer:
12
Step-by-step explanation:
You simply add the coefficients together.
3 + 4 + 5 = 12
How many minutes are not spent on instructions?

Answers
Answer: 1/5
Step-by-step explanation:
Answer:
I'm pretty sure the answer is 48 minutes!
An army camp had a food provision of 35 days for 800 soldiers on the first day of the month. On
the same day, some of the soldiers were transferred to another camp. The food provision lasted for
50 days for the remaining soldiers. How many soldiers were transferred to the other camp?
(Assume that each soldier consumes equal quantity of food per day.)
Answers
240 soldiers were transferred to the other camp. Let's assume the number of soldiers transferred to the other camp is "x." we can solve for the unknown variable representing the number of soldiers transferred.
Initially, the food provision was planned for 800 soldiers for 35 days. This means that the total food supply is equal to 800 soldiers multiplied by 35 days, which gives us a total of 28,000 soldier-days of food.
After some soldiers were transferred, the remaining soldiers had enough food to last for 50 days. So the food supply for the remaining soldiers can be calculated as the product of the number of remaining soldiers and the number of days, which gives us (800 - x) * 50 soldier-days of food.
Since the amount of food remains the same, we can set up the following equation:
\(28,000 = (800 - x) * 50\)
Now, let's solve this equation to find the value of x, representing the number of soldiers transferred to the other camp:
\(28,000 = 50 * 800 - 50x28,000 = 40,000 - 50x50x = 40,000 - 28,00050x = 12,000x = 12,000 / 50x = 240\)
By setting up the equation based on the total food supply for the initial and remaining soldiers, we can solve for the unknown variable representing the number of soldiers transferred. In this case, 240 soldiers were transferred to the other camp.
For more such questions on unknown variable.
https://brainly.com/question/20866805
#SPJ8
the null hypothesis for the sign test always states that the mean difference between the matched or paired samples is zero T/F
Answers
True. The null hypothesis for the sign test always states that the mean difference between the matched or paired samples is zero.
Therefore, the null hypothesis always states that the mean difference between the matched or paired samples is zero.Sign Test for Comparing Two Matched SamplesThe sign test is used to compare two related or matched samples to determine if they are significantly different from one another. It is based on the idea that the difference between two related samples should be zero. The null hypothesis of the sign test states that the mean difference between the two matched or paired samples is zero, meaning that there is no difference between the two samples.
The alternative hypothesis is that the mean difference between the two samples is not zero, indicating that there is a significant difference between the two samples. The sign test is used to determine if the two samples are significantly different from one another.
Learn more about Sign test: https://brainly.com/question/15980493
#SPJ4
5.3 MATHEMATICS HOLIDAY PACKAGE-TERM 2(2023) Instructions: Attempt ALL items 1. Your family has seven siblings; peter, John, Sarah, Joy, Ali, Mary and Ivan. There is an interval of 2 years between the ages of the children from Ivan to peter. Ivan is three years old. Task: Using an arrow diagram, explain the information about your family.
Answers
i need the answer to this question
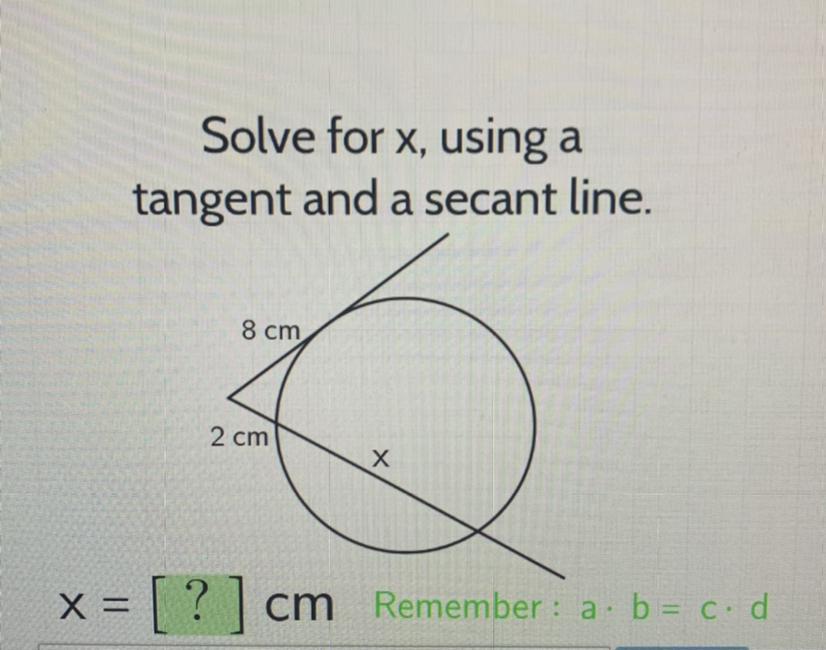
Answers
The measure of angle BAC is 55°, which is closest to option B (50°).
What is a tangent angle?The ratio of the length of the side directly opposite an acute angle to the side directly adjacent to the angle is known as the tangent in trigonometry. Only triangles with straight angles can have this.
Let's give the angles shown in the diagram the following labels:
Angle ACD = 55°
Angle ABD = 35°
Angle BCD = 90°
To determine the size of angle ABC, we can use the knowledge that a triangle's total angles equal 180°. Because the straight line formed by angles ABD and BCD, we have:
\(Angle ABC = 180° - Angles ABD and BCD.\)
\(Angle ABC = 180° - 35° - 90°Angle ABC = 55°\)
Given that triangle ABC has two angles, we can use the knowledge that a triangle's total of angles equals 180° to determine the size of angle BAC:
\(Angle BAC = 180° - Angle ABC - Angle ACBAngle BAC = 180° - 55° - 70°Angle BAC = 55°\)
To know more about angle visit:-
https://brainly.com/question/28451077
#SPJ1
It is most similar to option B (50°) when the angle BAC is 55°.
What is a tangent angle?
The tangent in trigonometry is the length of the side directly opposite an acute angle divided by the length of the side directly next to the angle.
This property can only be found in triangles with straight angles.
Let's give the angles shown in the diagram the following labels:
Angle ACD = 55°
Angle ABD = 35°
Angle BCD = 90°
We can use the fact that a triangle's total number of angles is 180° to calculate the size of angle ABC. due to the fact that the straight line created by angles ABD and BCD
Triangle ABC has two angles, so we can use the fact that a triangle's sum of angles is 180° to calculate the size of angle BAC.
Therefore, the BAC measurement is 55°, which is closest to option B's 50°.C is 55°, which is closest to option B (50°).
To know more about angle from the given link:-
brainly.com/question/28451077
#SPJ1
Help!! Factor the common factor out of each expression

Answers
Therefore , the solution of the given problem of equation comes out to be factor is (5b)(-5b+3).
What is the equation?A formula for connecting two statements using the equal sign (=) to denote equivalence is known as a mathematical equation. A mathematical equation in algebra is a statement that proves the equality of two mathematical expressions. For instance, the formula 3x + 5 = 14 places an equal sign between the variables 3x + 5 and 14. The mathematical relationship between the two sentences on either side of a letter is established. Most of the time, the symbol serves as both the one and only variable. for instance, 2x – 4 = 2.
Here,
the two numbers' primary factors are as follows:
-25\(b^{2}\) + 15b
Common prime factors can be multiplied to determine the GCF:
=> -25\(b^{2}\) = -(5)(5) * \(b^{2}\)
=> 15b = (5)(3)b
The expression can be factored in the following fashion because the GCF is 5b:
=> -(5)(5) * \(b^{2}\) + (5)(3)b
=> (5b)(-5b+3)
Therefore , the solution of the given problem of equation comes out to be factor is (5b)(-5b+3).
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
Which of the 2-values are solutions to the following inequality?
*> 150
Choose all answers that apply:
= 16
x=
x=151
x=200

Answers
Step by step
The greater than sign > means the number to the left of the sign is “greater than” , bigger, more than the number to the right.
One way of remembering which sign to use is to look at the sign as a mouth eating the bigger number. Example of our correct answers.
✅151 > 150 it’s eating the bigger number
✅200 > 150 it’s eating the bigger number
The less than sign < can be used with our incorrect answer 16
❌ 16 < 150
See, 16 is less than 150 and it is eating the bigger number.
I hope this helps
Zev read 15% of his 56-page book. Kelly read 12% of her 64-page book. Marneisha read 14% of his 68-page book Aleisha read 10% of her 72-page book. what the grastest
Answers
Answer:
Marneisha with 9.52 pages.
Step-by-step explanation:
Zev: 56×0.15 = 8.4
Kelly: 64×0.12 = 7.68
Marneisha: 68×0.14 - 9.52
Aleisha: 72×0.10 = 7.2