Answers
12+8+4+4+4+4+4+8=48
Related Questions
Given side lengths 4 units, 8 units, and x units, determine the range in which x must lie in order for a triangle to exist.
A)
X > 12
B)
0
C)-4
D)
4
Answers
Answer:
A is the correct answer
Step-by-step explanation:
Mathematically if we have lengths a, b and c
For a triangle to occur, let us say that the third side is c
then a + b must be greater than or equal to c
Hence c must be equal to (4 + 8) or greater than (4 + 8)
With the options given , A is the correct answer
In a histogram, the vertical line (dimension) shows the _____________, while the horizontal line (dimension) shows the _______________.
Answers
In the Histogram the horizontal line (dimension) represents the value of the selected collection plan element. The vertical line (dimension) represents the count or sum of occurrences of the primary collection element on the horizontal line.
learn more about Histogram here:
https://brainly.com/question/1230107
#SPJ1
Which expression represents a number that is 8 times as large as 19, 520 - 1,478?
Answers
Answer:the answer is 154682
Step-by-step explanation:
solve the following:
a/5 +3=8
and
3b/7 -1=5
Answers
B is false
I'm not sure the type of question
someone please help meeee !! I would really appreciate it

Answers
Answer:
cos 25° = X/11
and
sin 65° = X/11
is this good enough or do you need more workings?
Answer:
C = 90°
Step-by-step explanation:
The interior angles in every triangle are equal to 180 degrees. So, this means that
\( \alpha + \beta + \gamma \\ = 180 \: degrees\)
Which means that A + B +C = 180 degrees
A=25°
B = 65°
C =?
C = 180° - (A + B)
C = 180° - (25° +65°)
C = 180° - 90°
C = 90°
Please help?
1: The x-intercepts of a quadratic function are -3 and 5. What is the equation of its axis of symmetry?
#2: The solutions to a quadratic equation are x = 2 or x = -3. What are the x-intercepts of the related quadratic function?


Answers
Answer:
see explanation
Step-by-step explanation:
(1)
The axis of symmetry is situated midway between the x- intercepts, thus
x = \(\frac{-3+5}{2}\) = \(\frac{2}{2}\) = 1
Equation of axis of symmetry is x = 1 → d
-----------------------------------------------------
(2)
The x- intercepts of a quadratic are the solutions, thus
x = 2 and x = - 3 → b
help please! I am doing multivariable equations.

Answers
Answer:
(c+3b)/8 = a
Step-by-step explanation:
c = 8a -3b
Add 3b to each side
c +3b = 8a-3b+3b
c +3b = 8a
Divide each side by 8
(c+3b)/8 = 8a/8
(c+3b)/8 = a
Explanation: c=8a-3b, if you're wanted to solve for a you need to subtract 8a from both sides, c-8a=-3b then subtract c from both sides, -8a=-3b-c then divide both sides by -8 a=3/8b+c/8
The city of London, England, has an
elevation of 11 meters.
Which of these describes the elevation
of London?
below sea level
at sea level
above sea level
Answers
Answer:
above sea level
Step-by-step explanation:
Rodrigo entrena para una maraton todos los dias sale a correr a una pista de 6 kilimetros de longitud,el lunes da dos vueltas,el martes da una vuelta y un medio,el miercoles da una vuelta y un tercio,el jueves da dos vueltas y dos quintos,el viernes da una vuelta y dos tercios,y el sabado dio dos vueltas y tres cuartos cuantos kilometros recorrio por dia
Answers
Answer:
11.65 km / day
Step-by-step explanation:
We can calculate the amount of daily kilometer in the following way
First day: 2 * 6 = 12 km
Second day: 1.5 * 6 = 9 km
Third day: 1.333 * 6 = 8 km
Fourth day: 2.4 * 6 = 14.4 km
Sixth day: 1.666 * 6 = 10 km
on Saturday: 2.75 * 6 = 16.5 km
the average per day
(12 + 9 + 8 + 14.4 + 10 +16.5) / 6 = 11.65
11.65 km/day
Select the mean, median, mode and range of the following list of values.1, 2, 4,7Averages3.5None36MeanMedianRangeMode
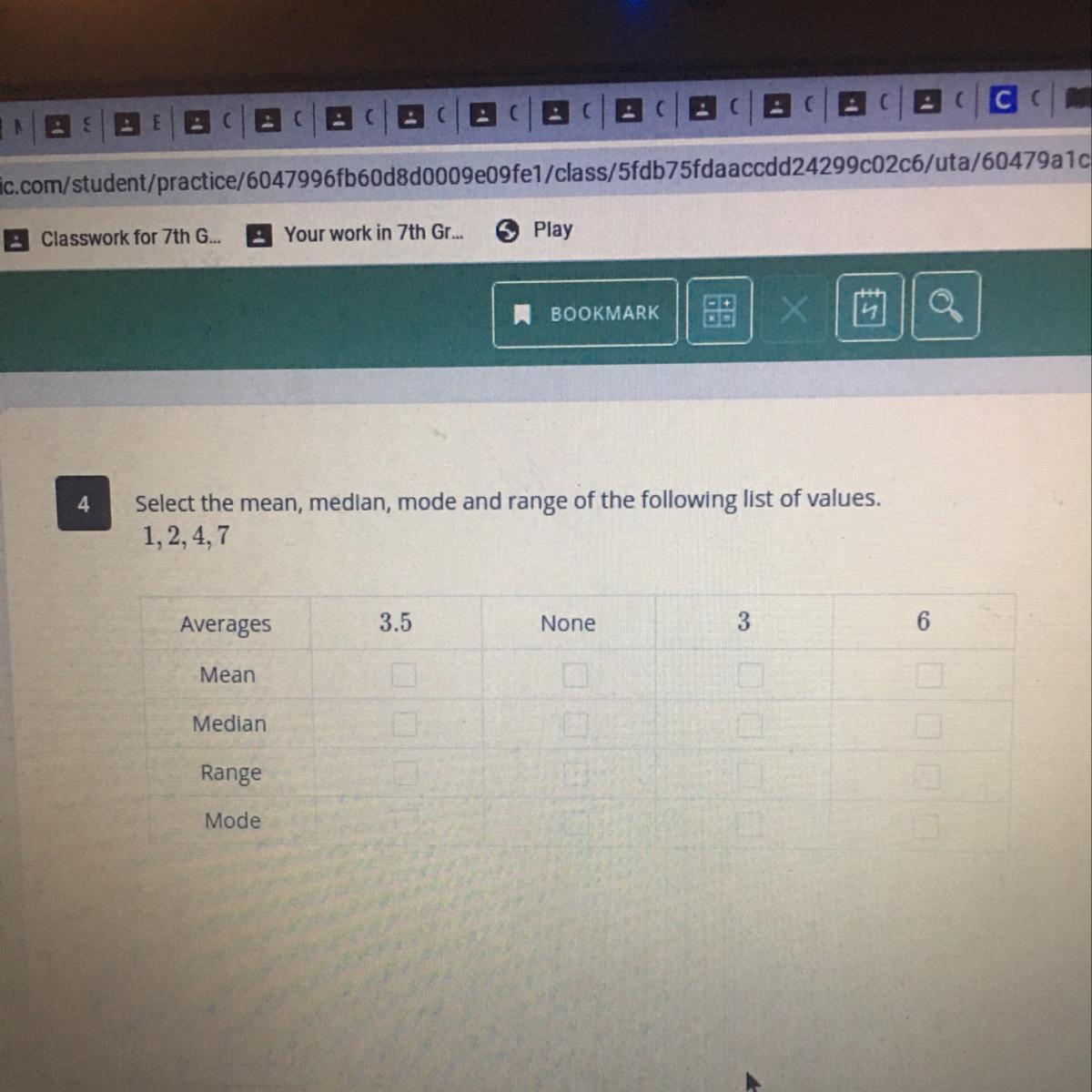
Answers
The data set is
1, 2, 4, 7
The answers are;
\(\begin{gathered} \text{Mean}=\frac{1+2+4+7}{4} \\ \text{Mean}=\frac{14}{4} \\ \text{Mean}=3.5 \end{gathered}\)\(\begin{gathered} \text{Median}=\frac{2+4}{2} \\ \text{Median}=\frac{6}{2} \\ \text{Median}=3 \end{gathered}\)The median in a case where the data set is an even number, then the median would take account of both middle values and then calculate addition of both and then divide by 2
The Mode is the most frequently occuring value in the data set. In this case, all observed data occur just once, and none of them occur more than once. Hence there is no Mode
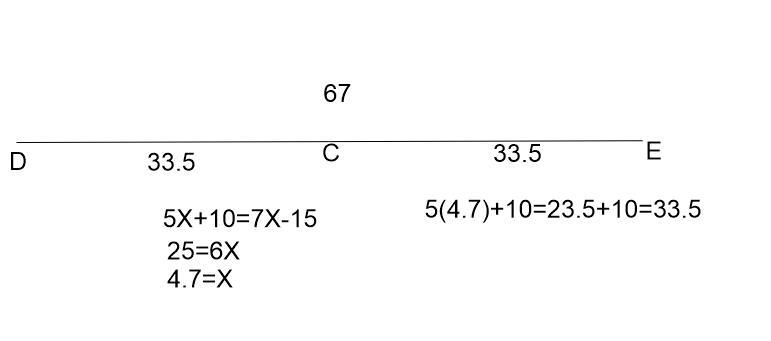
\(\begin{gathered} \text{Range}=\text{Highest value-Lowest value} \\ Range=7-1 \\ \text{Range}=6 \end{gathered}\)Let C be between point D and E.
Find the length of DC.
DC = 5x+10
DE = 67
CE = 7x-15
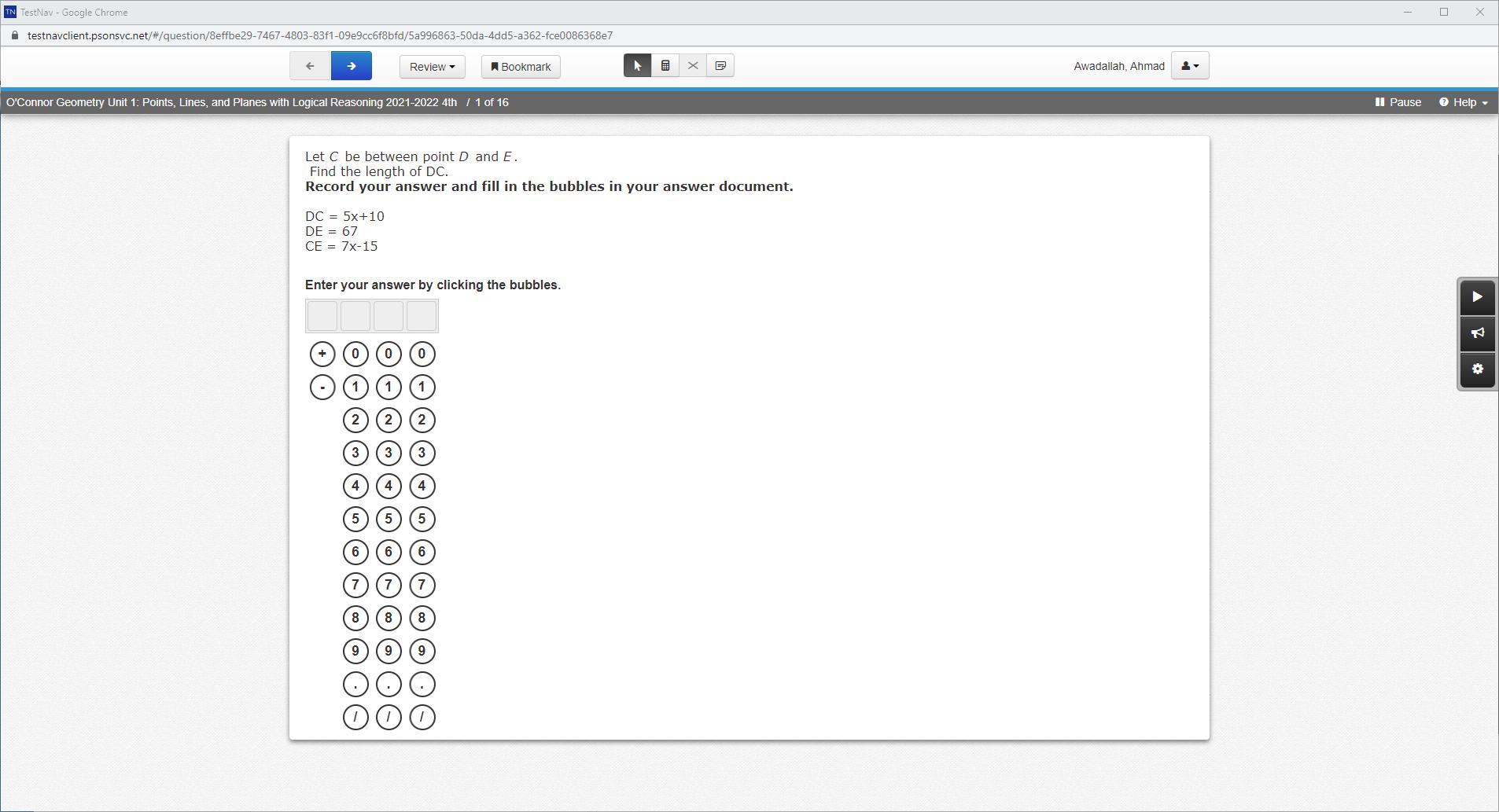
Answers
Answer:
DC = CE =33.5
Step-by-step explanation:
let f (x) = ⌊x2∕3⌋. find f (s) if a) s = {−2,−1,0,1,2,3}. b) s = {0,1,2,3,4,5}. c) s = {1,5,7,11}. d) s = {2,6,10,14}.
Answers
For the function f(x) = ⌊x²/3⌋, the values of f(s) for different sets s are as follows: a) f(s) = {1, 0, 0, 0, 1, 3}, b) f(s) = {0, 0, 1, 3, 5, 8}, c) f(s) = {0, 8, 16, 40}, d) f(s) = {1, 12, 33, 77}
The function f(x) = ⌊x²/3⌋ represents the floor of x²/3. To find f(s) for different sets s, let's evaluate it for each case:
a) For s = {-2, -1, 0, 1, 2, 3}:
- For -2, (-2)²/3 = 4/3, and ⌊4/3⌋ = 1.
- For -1, (-1)²/3 = 1/3, and ⌊1/3⌋ = 0.
- For 0, (0)²/3 = 0/3 = 0.
- For 1, (1)²/3 = 1/3, and ⌊1/3⌋ = 0.
- For 2, (2)²/3 = 4/3, and ⌊4/3⌋ = 1.
- For 3, (3)²/3 = 9/3 = 3.
Therefore, f(s) = {1, 0, 0, 0, 1, 3}.
b) For s = {0, 1, 2, 3, 4, 5}:
- For 0, (0)²/3 = 0/3 = 0.
- For 1, (1)²/3 = 1/3, and ⌊1/3⌋ = 0.
- For 2, (2)²/3 = 4/3, and ⌊4/3⌋ = 1.
- For 3, (3)²/3 = 9/3 = 3.
- For 4, (4)²/3 = 16/3, and ⌊16/3⌋ = 5.
- For 5, (5)²/3 = 25/3, and ⌊25/3⌋ = 8.
Therefore, f(s) = {0, 0, 1, 3, 5, 8}.
c) For s = {1, 5, 7, 11}:
- For 1, (1)²/3 = 1/3, and ⌊1/3⌋ = 0.
- For 5, (5)²/3 = 25/3, and ⌊25/3⌋ = 8.
- For 7, (7)²/3 = 49/3, and ⌊49/3⌋ = 16.
- For 11, (11)²/3 = 121/3, and ⌊121/3⌋ = 40.
Therefore, f(s) = {0, 8, 16, 40}.
d) For s = {2, 6, 10, 14}:
- For 2, (2)²/3 = 4/3, and ⌊4/3⌋ = 1.
- For 6, (6)²/3 = 36/3 = 12.
- For 10, (10)²/3 = 100/3, and ⌊100/3⌋ = 33.
- For 14, (14)²/3 = 196
The values of f(s) for the given sets show how the function ⌊x²/3⌋, which represents the floor of x²/3, behaves for different inputs.
Learn more about sets here: https://brainly.com/question/28860949
#SPJ11
A city grid of Anytown, USA is shown on the grid below. The fire department is represented by quadrilateral RSTU. Another fire department is opening in a different part of the city to maximize fire protection. The size of the new department's property must be congruent to the older department. Vertices A and B are plotted on the grid below to represent two vertices of the new fire department quadrilateral ABCD:
Map of Anytown. The line y equals 6 is Main Road. The line y equals 3 is Rose Lane. The line y equals negative 5 is Crystal Ave
What could be the ordered pairs representing vertices C and D of quadrilateral ABCD so that the new fire department is congruent to the old fire department? (4 points)
C(−7, 3), D(−7, 5)
C(2, 3), D(2, 5)
C(−2, 3), D(−2, 5)
C(0, 3), D(0, 5)

Answers
Answer:
C(0, 3), D(0, 5)Step-by-step explanation:
Points we are interested in given:
A(-4, 5), B(-4, 3)Points C and D have 2 possible places
1. To the left from A and B on the grid. They will have coordinates:
(-8, 3) and (-8, 5) (red points on the grid)2. To the right from A and B on the grid. They will have coordinates:
(0, 3) and (0, 5)Correct answer choice reflecting these coordinates is the last one which reflects the second option
Also see attached

Answer:
The answer is C!
Explanation:
I just took the test! :)
Bo's family and Lana's family each ate some pizza for dinner.Which statement correctly compares the fractions of each pizza that were eaten?
Answers
The question is incomplete
Is it possible to solve 3 equations with 4 variables?
Answers
A linear system with 3 equations and 4 variables by representing it with an augmented matrix and bringing the matrix to reduced row-echelon form can be solved.
What is linear system?A mathematical representation of a system based on the application of a linear operator is known as a "linear system" in systems theory. Ordinarily, compared to nonlinear systems, linear systems display much simpler features and properties. The automatic control theory, signal processing, and telecommunications all heavily rely on linear systems as a mathematical abstraction or idealisation.
Linear systems, for instance, are frequently used to model the propagation medium for wireless communication systems. An operator, H, that converts an input, x(t), into an output, y(t), a kind of black box description, can be used to describe a general deterministic system.
The superposition principle, or alternatively both the additivity and homogeneity properties, must be satisfied by a system to be considered linear, and only then.
Learn more about linear system
https://brainly.com/question/28977228
#SPJ4
Let C be the closed, piecewise smooth curve formed by traveling in straight lines between the points (0, 0, 0), (2, 1, 5), (1, 1, 3), and back to the origin, in that order. Use Stokes' theorem to evaluate the integral:
∫C(5xyz)dx+(3xy)dy+(x)dz
Use Stokes' Theorem to convert the line integral calculation into one involving a surface integral whose region of integration corresponds to the triangle bounded by the given vertices.
Answers
Using Stokes' theorem, the line integral can be converted to a surface integral over the triangle bounded by the given vertices. The surface integral can be evaluated by parameterizing the triangle and calculating the dot product with the curl of the vector field.
To evaluate the given line integral using Stokes' theorem, we first need to find the curl of the vector field F = (5xyz, 3xy, x). The curl of F is given by ∇ × F = (∂Q/∂y - ∂P/∂z, ∂P/∂z - ∂R/∂x, ∂R/∂x - ∂Q/∂y), where P = 5xyz, Q = 3xy, and R = x.
Calculating the partial derivatives, we have:
∂P/∂z = 5xy
∂Q/∂y = 3x
∂R/∂x = 1
Thus, ∇ × F = (5xy - 3x, 1 - 5xy, 3x - 3x) = (2x - 3, 1 - 5xy, 0).
Now, let's find the surface integral over the triangle bounded by the given vertices. We can parameterize the triangle using two variables u and v such that (u, v) lies in the region R: u ≥ 0, v ≥ 0, and u + v ≤ 1.
Using the parameterization, we have:
x = 2u + v,
y = u + v,
z = 5u + 3v.
Calculating the cross product of the partial derivatives ∂r/∂u and ∂r/∂v, we get ∂r/∂u × ∂r/∂v = (3, -1, 1).
The surface integral becomes ∫∫R (2u - 3, 1 - 5(2u+v)(u+v), 0) ⋅ (3, -1, 1) dA, where dA is the area element.
Integrating over the region R using these expressions, we can evaluate the surface integral and obtain the final result.
To learn more about Stokes' theorem click here brainly.com/question/29751072
#SPJ11
A green die and a red die are rolled. The random variable X is the absolute value of the difference between the number of spots on the red die and green die. Construct PMF, Random Variable, and Sample Space.
Answers
The random variable X shows the absolute difference between the number of spots on a green die and a red die rolled.
The Probability Mass Function (PMF) refers to the probability of each possible outcome, and the sample space is the set of all possible outcomes.
Suppose the red die and the green die, both of which have six sides numbered from 1 to 6.
The random variable X represents the absolute difference between the numbers rolled on the two dice. The values that X can take range from 0 to 5, the absolute difference cannot exceed 5.
To determine the PMF, we need to calculate the probability of each possible outcome. The sample space consists of all the possible combinations of rolls from the two dice, that means 36 in total (6 possibilities for the green die multiplied by 6 possibilities for the red die).
For each value of X, we find the number of combinations that yield that difference. when the green die rolls a 2 and the red die rolls a 4, the absolute difference is 2.
We count all such combinations for each value of X and divide it by the total number of combinations (36) to obtain the probability of each outcome.
The resulting PMF for X will have six entries, corresponding to the probabilities of X taking on the values 0, 1, 2, 3, 4, and 5. These probabilities will sum to 1, as they cover all possible outcomes.
Learn more about Probability Mass Function:
brainly.com/question/30765833
#SPJ4
Construct the confidence interval for the population mean μ c-0.95, x-4.8, σ-0.6, and n-55 A 95% confidence interval for μ is (LIL) . (Round to two decimal places as needed.)
Answers
Answer:
A 95% confidence interval for μ is (LIL) 4.61.
The confidence interval for the population mean μ is constructed as follows:
Here, x is the sample mean, σ is the population standard deviation,
n is the sample size, and
zα/2 is the z-value
that corresponds to a level of confidence of (1-α)100%.
Given that c = 0.95, x = 4.8, σ = 0.6, and n = 55.
Confidence interval is given by;
(LIL), (UIL) = (x - zα/2*σ/√n), (x + zα/2*σ/√n)
where LIL is the lower limit of the interval and UIL is the upper limit of the interval.
Now, we need to determine the value of zα/2 such that the level of confidence is 0.95.
In the standard normal distribution, the area to the left of
zα/2 is (1-α)/2 or
(1-0.95)/2 = 0.025.
Using the z-table, we can find that the z-value that corresponds to this area is 1.96.
Therefore, the 95% confidence interval for μ is given by;
(LIL), (UIL) = (4.8 - 1.96*0.6/√55), (4.8 + 1.96*0.6/√55)= (4.61, 4.99)
Therefore, a 95% confidence interval for μ is (LIL) 4.61. (Round to two decimal places as needed.)
Learn more about confidence interval, visit here
https://brainly.com/question/15712887
#SPJ11
The circumference of a circle is 27.632 meters. What is the circle's diameter?
Answers
Answer: ^^heya
your answer is ≈ 8.8
Step-by-step explanation:
C=2πr
d=2r
\(\\d=\) \(\frac{c}{\pi} =\frac{27.63}{\pi} = 8.79554\)
rounded answer ≈ 8.8
Answer:
D=8.8m
Step-by-step explanation:
d=c/π
27.632/3.14=8.8
D=8.8m
Which expression is equivalent to 50En-1(n(4n+3))

Answers
Answer:
equivalent of 50En-1+n(4n+3))is4{50(50+1)(2×60+1)+3{50(51)_2}
Answer: D
Step-by-step explanation: Im from the future D is correct on edge yw :)
HELP
6.{6.G.A.4} Find the surface area. Answer without units.
8 cm
7 cm
16 cm
7 cm

Answers
Step-by-step explanation:
Triangle
\(7 \times 8 \div 2 = 28\)
Rectangle
\(16 \times 7 = 112\)
Total
\(112 + 28 = 140\)
Un campanario tarda 4s en tocar 5 campanadas , ¿Cuanto tardara en tocar 10 campanadas?
Answers
¿Cuanto tardara en tocar 10 campanadas?
If 7/2 litre petrol cost 2163/8 find the cost of 4 litre petrol
Answers
The cost of 4 liters of petrol is 618.
To find the cost of 4 liters of petrol, we can use a proportion. Which means we will equate the two sides of equation having proportions.
We know that 7/2 liters of petrol cost 2163/8. We can write this as,
(7/2) / (2163/8) = 4 / x
where x is the cost of 4 liters of petrol.
To solve for x, we can cross-multiply,
(7/2) * x = (2163/8) * 4
Simplifying both sides, we get,
x = (2163/8) * 4 * (2/7)
x = 309 * 2
x = 618
Therefore, 4 liters of petrol is 618 in price according to question.
To learn more about cost here:
https://brainly.com/question/17369655
#SPJ4
Answer the question all the info you need is in the photo

Answers
Answer:
inches something grows every month
x&y
independent - months
dependent - inches
Step-by-step explanation:
a. look at the y and x labels and make a statement along the lines of {y} grows {x}
b. x and y axis (inches is y, months is x)
c. the independent variable grows on its own. it is generally on the x axis
d. the dependent variable grows based on the other variable it interacts with. usually on the y axis
Answer + method / explanation please

Answers
The expressions for the lengths of the segments obtained using vectors notation are;
a. i. \(\overrightarrow{LA}\) = q - (1/2)·p ii. \(\overrightarrow{AN}\) = (2/7)·(p - q)
b. The expressions for \(\overrightarrow{MN}\), \(\overrightarrow{LA}\), and \(\overrightarrow{AN}\) indicates;
\(\overrightarrow{MN}\) = (1/84)·(46·q - 11·p)
What are vectors?A vector is a quantity that has magnitude and direction and are expressed using a letter aving an arrow in the form, \(\vec{v}\)
a. i. \(\overrightarrow{LA}\) = \(\overrightarrow{BA}\) - \(\overrightarrow{LB}\) = \(\overrightarrow{BA}\) - (1/2) × \(\overrightarrow{CB}\)
\(\overrightarrow{BA}\) - (1/2) × \(\overrightarrow{CB}\) = q - (1/2)·p
\(\overrightarrow{LA}\) = q - (1/2)·p
ii. \(\overrightarrow{AC}\) = \(\overrightarrow{BC}\) - \(\overrightarrow{BA}\)
\(\overrightarrow{AN}\) = (2/7) × \(\overrightarrow{AC}\)
\(\overrightarrow{AN}\) = (2/7) × \(\overrightarrow{BC}\) - \(\overrightarrow{BA}\)
\(\overrightarrow{AN}\) = (2/7) × (p - q)
b. \(\overrightarrow{MN}\) = \(\overrightarrow{MA}\) + \(\overrightarrow{AN}\)
\(\overrightarrow{MA}\) = (5/6) × \(\overrightarrow{LA}\)
\(\overrightarrow{LA}\) = q - (1/2)·p
\(\overrightarrow{AN}\) = (2/7) × (p - q)
Therefore;
\(\overrightarrow{MN}\) = (5/6) × ( q - (1/2)·p) + (2/7) × (p - q)
\(\overrightarrow{MN}\) = (1/84) × ( 70·q - 35·p + 24·p - 24·q) = (1/84)(46·q - 11·p)
Learn more on the vectors here: https://brainly.com/question/2375446
#SPJ1
In a school with 300 students 18% of the students take violin lessons and 6% of the students take clarinet lessons.
A: find the number of students who take each type lesson.
B: How many more students take violin than take clarinet lessons?
Answers
A) 54 violin students and 6 clarinet students
B) 36 more students
Explanation:
300 students * 0.18 (which is 18%) = 54 students
300 students * 0.06 = 18 students
54-18=36
Hope this helps :)
Pete grabbed 18 mixed nuts 2/9 of which were almonds . Which equation shows how to determine the number of almonds pete grabbed. A. 18 divided by 2/9=81 B.18 times 2/9=4 C.2/9 divided by 18 = 1/81 D. 9/2 divided by 18= 4/1
Answers
Answer:
B.18 times 2/9=4
Step-by-step explanation:
Given that :
Number of mixed nuts grabbed by pete = 18
Fraction of almonds = 2/9
Number of almonds grabbed by pete :
Fraction grabbed × number of mixed fruits grabbed
2/9 × 18
= 36 / 9
= 4
Hence, Pete grabbed 4 almonds
Matt draws a line through the points (-7, 3) and (-5, -1). What is the slope of this line?
Answers
Answer:\(-\frac{2}{1}\)
Step-by-step explanation:
Find the slope of a line that passes through the points (-7, 3) and (-5, -1).
Plug in the two points into \(\frac{y_{2} - y_{1} }{x_{2} -x_{1} }\) and solve.
\(\frac{(-1)-(3)}{(-5)-(-7)}\) = \(\frac{-4}{2}\)
Simplify the fraction.
\(\frac{-4}{2}\) →\(\frac{-2}{1}\)
The slope of this line would be \(-\frac{2}{1}\).
Help me with this I will give you brainlist

Answers
Answer:
3/20
Step-by-step explanation:
Of means multiply. When it says 3/10 of 4/8, it just means 3/10*4/8 which when multiplied across gives you 12/80. Which can be simplified to 3/20.
Hope this helps.
Find the value of x. Round your answer to the nearest tenth

Answers
Answer:
15.9
Step-by-step explanation:
