Find the probability the next person you meet was born either on a Monday or a
Friday.
Show all relevant work. To type a fraction, use the forward slash key on your
keyboard (/), i.e., "1/2". To type an exponent, use the caret (^), i.e., "2^5".

Answers
Answer: The probability is 2/7.
Step-by-step explanation:
Ok, suppose you meet a random person.
The possible days in which that person was born are the seven days of the week, so the total number of outcomes is 7, and we will assume that the probability is evenly distributed for all the days.
Now, we want to calculate the probability that this person was born on a Monday or a Friday.
So we have 2 possible outcomes out of 7.
Then the probability will be equal to the quotient between number of of outcomes that meet the conditions (Monday and Friday, 2 outcomes) and the total number of outcomes (7)
P = 2/7
Related Questions
pls help asap pls i pay 54

Answers
The value of BC is 9cm.
What is a similar triangle?
If two triangles have the same shape or have the same shape as their mirror images, they are said to be comparable. One can be created from the other more precisely by evenly scaling, possibly with the inclusion of further translation, rotation, and reflection.
Here, we have
Given: BA = 6cm, AC = 8cm
BC =?
In a similar triangle, their side is also proportional.
BA/ED = AC/DF = BC/EF
BA/ED = BC/EF
6/18 = BC/27
18BC = 6×27
BC = 6×27/18
BC = 9cm
Hence, the value of BC is 9cm.
To learn more about a similar triangle from the given link
https://brainly.com/question/14285697
#SPJ1
Can anyone help me with this problem??

Answers
9514 1404 393
Answer:
(a) 4/3
(b) y -3 = 4/3(x -1)
(c) y -3 = -3/4(x -1)
(d) r = 5
Step-by-step explanation:
a) The slope is given by the slope formula:
m = (y2 -y1)/(x2 -x1)
m = (7 -3)/(4 -1) = 4/3
__
b) The radius is normal to the circle. The point-slope form of the equation for a line can be useful here:
y -k = m(x -h) . . . . . line with slope m through point (h, k)
For slope 4/3, the line through point (1, 3) will have the equation ...
y -3 = 4/3(x -1) . . . . point-slope equation of the normal
__
c) The tangent is perpendicular to the radius. It will have a slope that is the opposite reciprocal of the slope of the radius: -1/(4/3) = -3/4.
y -3 = -3/4(x -1) . . . . point-slope equation of the tangent
__
d) The radius can be found from the distance formula.
d = √((x2 -x1)² +(y2 -y1)²)
d = √((4 -1)² +(7 -3)²) = √(3² +4²) = √25 = 5
The radius of the circle is 5.

Which statement is true about the function shown in the graph?

Answers
Answer:
A
Step-by-step explanation:
The function that is shown in the graph is strictly decreasing
What is a function?"A function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function."
The given function has a value of (- 5) at a certain point.
After that the function is decreased to a value of (- 10).
Therefore, we can conclude that the function is strictly decreasing.
Learn more about a function here:
https://brainly.com/question/11943224
#SPJ2
Maria made $273 for 13 hours of work. at the same rate, how many hours would she have to work to make $189?

Answers
Answer:
9 hours
Step-by-step explanation:
$273/13 hours=$21 per hour
$189/$21 =9 hours
Oil change at Citi auto is regular $30 Mr. Allen has a coupon for 15% off he wants to know the sale price of the service which equation can be used to find the cell price S of an oil change

Answers
S = 30 - 0.15(30) or S = 0.85 can be used to calculate the sale price S of an oil change (30).
What are an example and an equation?By resolving this equation, we find that the value of the variable x is 7. An equation is a mathematical formula that states that two quantities or values are equal, as in the example 6 x 4 = 12 x 2.
S will serve as a stand-in for the sale price of the oil change.
Mr. Allen has a 15% off voucher, and the oil change normally costs $30. The reduction can be shown as 15% of the standard price, or:
0.15 * $30 = $4.50
We can deduct the discount from the list price to determine the oil change's selling price:
S = $30 - $4.50
S = $25.50
As a result, S = 30 - 0.15 can be used to calculate the sale price S of an oil change (30)
To know more about sale price visit:-
https://brainly.com/question/29363568
#SPJ1
Answer:
The answer is s=0.85*30=22.50(final sale price) which will be 15 % of the 30 dollars
Step-by-step explanation:
the original price: $75 and percent of discount :30% what’s the
Answers
Answer:
The discount is 22.50 and the final price $52.50
Step-by-step explanation:
Discount = Original Price x Discount %/100
Discount = 75 × 30/100
Discount = 75 x 0.3
You save = $22.50
Final Price = Original Price - Discount
Final Price = 75 - 22.5
Final Price = $52.50
7.0 is ten times as much as
Answers
Answer:
0.7
Step-by-step explanation:
Answer:
0.7
Step-by-step explanation:
e2020
A 10 meter ladder is leaned up against a building. If
the angle of elevation is 60 degrees, what is the
height of the building?
Answers
Answer:
8.7
Step-by-step explanation:
Use trigonometry. The ladder and the building form a right triangle with the ground. You are given the length of the hypotenuse and the base angle. You use sine since we are trying to figure out the opposite side from the angle and we have the hypotenuse length. Sin = opposite/hypotenuse. So in this case, sin 60°= x/10. We solve for x by multiplying both sides by 10. Now x= sin 60° (10) = (0.8660)(10) = 8.7 m.
If x + 1/9x = 1, then find the value of 27x³ + 1/27x³ = ?
Answers
\(\large\underline{\sf{Solution-}}\)
Given:
\( \sf \longmapsto x + \dfrac{1}{9x} = 1\)
Multiplying both sides by 3, we get:
\( \sf \longmapsto 3 \bigg(x + \dfrac{1}{9x} \bigg) = 3 \times 1\)
\( \sf \longmapsto 3x + \dfrac{1}{3x} = 3\)
Cubing on both sides, we get:
\( \sf \longmapsto \bigg(3x + \dfrac{1}{3x} \bigg)^{3} = {3}^{3} \)
\( \sf \longmapsto {(3x)}^{3} + \bigg(\dfrac{1}{3x} \bigg)^{3} + \bigg(3 \times {(3x)}^{2} \times \dfrac{1}{3x} \bigg) + \bigg(3 \times 3x\times \bigg( \dfrac{1}{3x} \bigg)^{2} \bigg) = {3}^{3} \)
\( \sf \longmapsto 27{x}^{3} + \dfrac{1}{27x^{3}} + 9x + \dfrac{1}{x} = {3}^{3} \)
\( \sf \longmapsto 27{x}^{3} + \dfrac{1}{27x^{3}} + 9 \bigg(x + \dfrac{1}{9x} \bigg) = 27\)
As we know that:
\( \sf ,\red\longmapsto x + \dfrac{1}{9x} = 1\)
We get:
\( \sf \longmapsto 27{x}^{3} + \dfrac{1}{27x^{3}} + 9 \times 1 = 27\)
\( \sf \longmapsto 27{x}^{3} + \dfrac{1}{27x^{3}} + 9 = 27\)
\( \sf \longmapsto 27{x}^{3} + \dfrac{1}{27x^{3}} = 18 \: Ans.\)
I need help on this part

Answers
Answer:
ang 4 = 60°
Step-by-step explanation:
ang 1 and ang 4 are Linear pair or supplementary angles.
ang 1 + ang 4 = 180
120° + ang 4 = 180° (Putting the value of ang 1)
ang 4 = 180° - 120°
ang 4 = 60°
Kristin draws a different circle. The radius of Kristin's circle is 1/2 the radius of Ben's circle. Which statement is true about Kristin's
circle?
O A The area of Kristin's circle is 2 times the area of Ben's circle.
OB. The area of Kristin's circle is 4 times the area of Ben's circle.
C. The area of Kristin's circle is 1/4 the area of Ben's circle.
D. The area of Kristin's circle is 1/2 the area of Ben's circle
Help please hurry !!
Answers
Answer:
\(\large\boxed{\textsf{Option D.}}\)
Step-by-step explanation:
\(\textsf{For this problem, we are asked to compare the areas between Kristin's and Ben's circle.}\)
\(\textsf{To start, we should know that the Radius plays an important role for the area.}\)
\(\Large\underline{\textsf{What is the Radius?}}\)
\(\textsf{The \underline{Radius} is a \underline{line segment} that starts at the \underline{center} of the circle, and ends at}\)
\(\textsf{a point on the \underline{circumference} of the circle. (\underline{Arc})}\)
\(\large\underline{\textsf{Area of a Circle:}}\)
\(\mathtt{Area = \pi (radius)^{2}}\)
\(\textsf{The Radius \underline{determines} what the area of the circle is.}\)
\(\textsf{Because Kristin's radius is 1/2 of Ben's radius, \underline{the area will be 1/2 of Bens}.}\)
\(\large\boxed{\textsf{Option D.}}\)
giving brainliest (don’t need to explain)
-
-
solve for x: 3(2x+54)-(27x-3)=56
Answers
Answer:
x = 109/21
Step-by-step explanation:
Step 1: Write equation
3(2x + 54) - (27x - 3) = 56
Step 2: Solve for x
Distribute: 6x + 162 - 27x + 3 = 56Combine like terms: -21x + 165 = 56Subtract 165 on both sides: -21x = -109Divide both sides by -21: x = 109/21The function f(x)=−3x+2 is defined over the domain −1
Answers
The domain of the function f(x) = -3x + 2 is (-∞, +∞), representing all real numbers, and the range is (-∞, 2], representing all real numbers less than or equal to 2.
The function f(x) = -3x + 2 is a linear function defined by a straight line. To determine the domain of this function, we need to identify the range of values for which the function is defined.
The domain of a linear function is typically all real numbers unless there are any restrictions. In this case, there is no explicit restriction mentioned, so we can assume that the function is defined for all real numbers.
Therefore, the domain of the function f(x) = -3x + 2 is (-∞, +∞), which represents all real numbers.
Now, let's analyze the range of the function. The range of a linear function can be determined by observing the slope of the line. In this case, the slope of the line is -3, which means that as x increases, the function values will decrease.
Since the slope is negative, the range of the function f(x) = -3x + 2 will be all real numbers less than or equal to the y-intercept, which is 2.
Therefore, the range of the function is (-∞, 2] since the function values cannot exceed 2.
For more such question on function. visit :
https://brainly.com/question/11624077
#SPJ8
Plz help me! Thank you

Answers
Answer:
Thank yoooooooouuuuuuuuu :)
Brittany buys 2.55 pounds of turkey for $5.96 per pound and 3.7 pounds of
cheese for $3.35 per pound. She gave the clerk twenty dollars. How much
more money does Brittany need? Include your units.
Answers
Answer:
Brittany needs another $3.7405.
Step-by-step explanation:
Per pound Cost of turkey = $5.96 per pound
The amount Brittany buys the turkey = 2.55 pounds
Brittany's cost for turkey = 2.55 × $5.96 = $15.198
Per pound cost for cheese = $3.35 per pound
The amount Brittany buys the cheese = 3.7 pounds
Brittany's cost for cheese = 2.55 × $3.35 = $8.5425
So,
Brittany's total cost = Turkey cost + Cheese cost
= $15.198 + $8.5425
= $23.7405
As brittany gave the clerk 20 dollars.
So, the amount she further needs will be:
$23.7405 - $20 = $3.7405
Therefore, Brittany needs another $3.7405.
Find the missing side

Answers
By using trigonometry, the missing sides are
Example 1: x = 16.7
Example 2: x = 3.2
Example 3: x = 23.5
Example 4: x = 9.3
Trigonometry: Determining the values of the missing sidesFrom the question we are to determine the value of the missing sides in the given triangles
We can determine the value of the missing sides by using SOH CAH TOA
Example 1
Angle = 42°
Opposite side = x
Hypotenuse = 25
Thus,
sin (42°) = x / 25
x = 25 × sin (42°)
x = 16.7
Example 2
Angle = 75°
Opposite side = 12
Adjacent side = x
Thus,
tan (75°) = 12 / x
x = 12 / tan (75°)
x = 3.2
Example 3
Angle = 36°
Hypotenuse side = x
Adjacent side = 19
Thus,
cos (36°) = 19 / x
x = 19 / cos (36°)
x = 23.5
Example 4
Angle = 53°
Opposite side = x
Adjacent side = 7
Thus,
tan (53°) = x / 7
x = 7 × tan (53°)
x = 9.3
Hence,
The missing sides are 16.7, 3.2, 23.5 and 9.3
Learn more on Trigonometry here: https://brainly.com/question/29195940
#SPJ1
-20 = -5 - 3x I need help on this
Answers
Answer:
x=5
Step-by-step explanation:
add 5 to both sides
-20+5 = -3x
-15=-3x (divide)
x=5
Can someone help and explain? 4 + 5x - 1
Answers
Answer:
5x+3
Step-by-step explanation:
1. Subtract 1 from 4
4+5x-1
2. Solution
5x+3
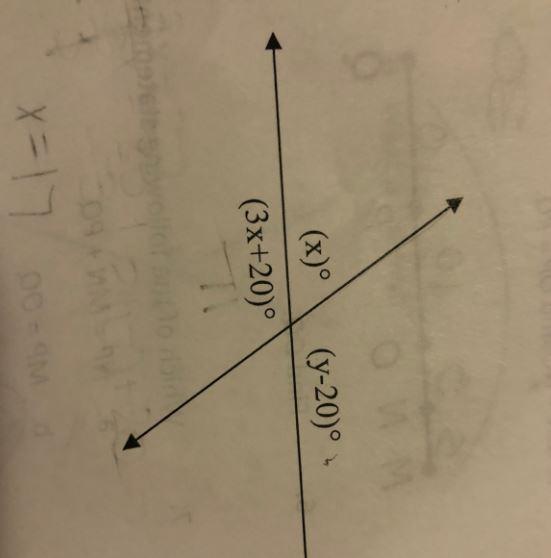
Will mark brainliest.

Answers
The solution is, the value of the variables are x = 40 and, y = 160.
Notice that "x" and "3x+20" are supplementary angles so their sum is 180°
(x) + (3x + 20) = 180
4x + 20 = 180
4x = 160
x = 40
To solve for "y", you have 2 options: either notice that "x" and "y-20" are supplementary angles so their sum is 180° or notice that "3x + 20" and "y - 20" are vertical angles so are equal to each other. I am going to solve using the first option because it is less work.
(x) + (y - 20) = 180°
40 + y - 20 = 180
y + 20 = 180
y = 160
Answer: x=40, y=160
The solution is, the value of the variables are x = 40 and, y = 160.
To learn more on angle click:
brainly.com/question/28451077
#SPJ1
complete question:
Find the value of each variable
You believe that requiring students to attend a series of presentations on study skills will improve their grades. You are concerned that boys and girls might react differently to such a series, and that students in grades 9 and 10 might react differently than those in grades 11 and 12. You set up an experiment involving 100 students in ninth and tenth grade and 100 students in eleventh and twelfth grade. (Assume there are equal numbers of girls and boys in each grade.) You intend to measure improvement based on pre- and post-treatment grade-point averages. A. Describe the design of an experiment to help you determine if a set of presentations on study skills is effective in improving grades. AP Statistics Page 5 of 13 Exam: Final Exam User Name: Instructor: Date: (print clearly) B. Suppose you have 50 students and need to assign them to two groups of equal size. Describe a randomization procedure that would achieve this. C. Suppose you have 50 students and need to assign them to two independent groups. Describe a randomization procedure that would achieve this.
Answers
Answer:
it will be equal and keep it up you will make good grades
Step-by-step explanation:
The design of an experiment in the research to help determine if a set of presentations is simply to consider two groups depending on the gender.
What is a research?It should be noted that a research simply means an enquiry that is done to achieve a particular information.
In this case, the design of an experiment in the research to help determine if a set of presentations is simply to consider two groups depending on the gender.
Also, the randomization procedure that would achieve this is the ANOVA.
Learn more about research on:
https://brainly.com/question/968894
#SPJ2
Does anyone know the answer to this?!!!!!

Answers
Answer:
D
Step-by-step explanation:
your domain is all ur X values while ur range is all y values. Just look at the points and determine the coordinates, all the X values belong to the domain and all y values belong to the range
hope this helps
Hope this helps love
y - ( -3y ) what is the answer????
Answers
Answer:
4y
Step-by-step explanation:
y - -3y
Subtracting a negative is like adding
y+3y
Combine like terms
4y
Answer:
\(4y\)
Step-by-step explanation:
\(y - ( - 3y) \\ y + 3y \\ = 4y\)
hope this helps
brainliest appreciated
good luck! have a nice day!
U
14 poi
At the college football game there were 48,000 people. If 77% of the
people at the game were supporters for the home team, how many
people were supporting the home team? *
Answers
Answer:
36960 people
Step-by-step explanation:
Answer:
36,960 people
Step-by-step explanation:
\(\frac{is}{of}=\frac{percent}{100}\) is the formula to solve for this equation, here plugging in all our numbers gives us \(\frac{x}{480,000} = \frac{77}{100}\).
We do not know our "is" so we replace it for x and solve → \(x=(480,000)(\frac{77}{100} )\) = 36,960 people
Help me please, which postulate proves these two triangles are congruent?

Answers
Answer:
C
Step-by-step explanation:
These triangles do look congruent. However, in fact, we don’t have enough information. We need 3 parts of a trainable to be shown congruent for it to be congruent, including HL congruence (because this requires a right angle). In the diagram, only 2 sides are shown to be congruent. This isn’t enough information to prove that the triangles are congruent. Therefore, it is C.
I hope this helps! :)
Construct a polynomial function with the following properties: fifth degree, 4 is a zero of multiplicity 3, −2 is the only other zero, leading coefficient is 2.
Answers
Answer:
\(\Large \boxed{\sf \bf \ \ 2(x-4)^3(x+2)^2 \ \ }\)
Step-by-step explanation:
Hello, please consider the following.
Construct a polynomial function with the following properties...
... fifth degree
It means that the polynomial can be written as below.
\(a_5x^5+a_4x^4+a_3x^3+a_2x^2+a_1x+a_0 \ \text{ with }a_5\text{ different from 0}\\\\\text{ or } k(x-x_1)(x-x_2)(x-x_3)(x-x_4)(x-x_5) \\\\ \text{ with k different from 0 and } (x_i)_{1\leqi\leq 5 } \text { are the roots.}\)
... 4 is a zero of multiplicity 3
We can write the polynomial as below.
\(k(x-4)(x-4)(x-4)(x-x_4)(x-x_5)=k(x-4)^3(x-x_4)(x-x_5)\)
... −2 is the only other zero
Because this is the only other zero, we can deduce that -2 is a zero of multiplicity 2.
\(k(x-4)(x-4)(x-4)(x-x_4)(x-x_5)\\\\=k(x-4)^3(x-(-2))(x-(-2))\\\\=k(x-4)^3(x+2)^2\)
... leading coefficient is 2.
Finally, it means that k = 2 and then the polynomial function is:
\(\large \boxed{2(x-4)^3(x+2)^2}\)
Hope this helps.
Do not hesitate if you need further explanation.
Thank you
To change a mixed number to an improper fraction, you do the following
W(d)+n
d
True or False.
True
False

Answers
Answer:
true
Step-by-step explanation:
A parking lot is given by the diagram below. Find the perimeter of the parking lot in terms of x

Answers
Answer:
\(2x^{2} - 11x - 11\)
Step-by-step explanation:
The solution is, the perimeter of the parking lot in terms of x is,
2 ( 2x² -11x -6 ) ft.
What is perimeter?A perimeter is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length. The perimeter of a circle or an ellipse is called its circumference. Calculating the perimeter has several practical applications.
here, we have,
from the given figure, we get,
the length of one side = (3x +12) ft
the length of one side = 5x ft
the length of one side = ( 6x - 14 ) ft
the length of one side = (4x+1) ft
the length of one side = ( x² -12x +10) ft
the length of one side = (x² +x -16) ft
now, we know that,
the perimeter = the sum of lengths of out side
so, we get,
perimeter = 2 ( x² -12x +10 + x² +x -16 )
= 2 ( 2x² -11x -6 )
Hence, The solution is, the perimeter of the parking lot in terms of x is,
2 ( 2x² -11x -6 ) ft.
Learn more about perimeter here:
brainly.com/question/397857
#SPJ2
cube m holds a maximum of 64 unit cubes. each unit cube has an edge length of 1/2 centimeter. what is the length of cube m?
Answers
Answer:
136 or 34
Step-by-step explanation:
not sure if its right because my math is bad
The value of 3 in 783.97
Answers
Answer:
place value of 3 in 783.97 is 3
Step-by-step explanation:
Answer:
Units
Step-by-step explanation:
The units start counting from 3 because after the point that is the 9 start counting tenth
Use vectors to find the interior angles of the triangle with the given vertices. (Enter your answers as a comma-separated list. Enter your answers in terms of degrees. Round your answers to two decimal places.)
(−2, 4), (−3, 8), (6, 8)
Please Help ASAP
Answers
Answer:
77.47°
75.96°
26.57°
Step-by-step explanation:
Given vertices of the triangle:
A = (−2, 4)B = (−3, 8)C = (6, 8)Find the vectors from A to B, B to C and A to C:
\(\begin{aligned}AB = B - A &=(x_B-x_A,y_B-y_A) \\&=(-3-(-2), 8-4)\\& = (-1, 4) \end{aligned}\)
\(\begin{aligned}BC=C-B &=(x_C-x_B,y_C-y_B)\\ &=(6-(-3),8-8)\\&=(9,0)\end{aligned}\)
\(\begin{aligned}AC = C - A &=(x_C-x_A,y_C-x_A)\\&= (6-(-2), 8-4) \\&= (8, 4)\end{aligned}\)
Use Pythagoras Theorem to calculate the magnitudes of the vectors:
\(|AB| = \sqrt{(-1)^2+4^2}=\sqrt{17}\)
\(|BC|=\sqrt{9^2+0^2}=9\)
\(|AC| = \sqrt{8^2+4^2}=4\sqrt{5}\)
\(\boxed{\begin{minipage}{6 cm}\underline{Dot Product of two vectors}\\\\$a \cdot b=|a||b| \cos \theta$\\\\where:\\ \phantom{ww}$\bullet$ $|a|$ is the magnitude of vector a. \\ \phantom{ww}$\bullet$ $|b|$ is the magnitude of vector b. \\ \phantom{ww}$\bullet$ $\theta$ is the angle between $a$ and $b$. \\ \end{minipage}}\)
Rearrange the dot product formula to make θ the subject:
\(\implies \theta=\cos^{-1}\left(\dfrac{a \cdot b}{|a||b|}\right)\)
Use the rearranged dot product formula to find the angles between two pairs of vectors.
\(\boxed{\begin{minipage}{4 cm}\underline{Dot Product}\\\\$\textbf{u} \cdot \textbf{v}=u_1v_1+u_2v_2$\\\\where:\\ \phantom{ww}$\bullet$ $\textbf{u}=\left\langle u_1,u_2 \right\rangle$ \\\phantom{ww}$\bullet$ $\textbf{v}= \left\langle v_1,v_2 \right\rangle$ \\ \end{minipage}}\)
Angle A
\(\implies A=\cos^{-1}\left(\dfrac{AB \cdot AC}{|AB||AC|}\right)\)
\(\implies A=\cos^{-1}\left(\dfrac{-1 \cdot 8+4 \cdot4}{\sqrt{17} \cdot 4 \sqrt{5}}\right)\)
\(\implies A=\cos^{-1}\left(\dfrac{8}{4 \sqrt{85}}\right)\)
\(\implies A=77.47^{\circ}\; \sf (2 \; d.p.)\)
Angle C
\(\implies C=\cos^{-1}\left(\dfrac{BC \cdot AC}{|BC||AC|}\right)\)
\(\implies C=\cos^{-1}\left(\dfrac{9 \cdot 8+0 \cdot4}{9 \cdot 4 \sqrt{5}}\right)\)
\(\implies C=\cos^{-1}\left(\dfrac{72}{36 \sqrt{5}}\right)\)
\(\implies C=26.57^{\circ}\; \sf (2 \; d.p.)\)
Interior angles of a triangle sum to 180°.
\(\implies B=180^{\circ}-A-C\)
\(\implies B=180^{\circ}-77.47^{\circ}-26.57^{\circ}\)
\(\implies B=75.96^{\circ}\)
Therefore, the interior angles of the triangle with the given vertices are:
77.47°75.96°26.57°