Find the product
-1/2y(2y^3-8)
Answers
Answer:
-y^4+4y
Step-by-step explanation:
Related Questions
a < 0 what dose that mean
Answers
a is smaller than 0.
on the natural numbers scale on the left side of value 0 are negative numbers.
Answer:
anything under 0 such as -1 -2 -3 -4 and anything below so you write any number below 0
Find the area of the regular polygons and degree of central angle when given either the apothem or side length.

Answers
The length of the apothem is 10. 99cm
How to determine the valuesTo determine the apothem of a polygon, we have to use the formula;
a = s/2 tan (180/n)
Such that the parameters are;
a is the length of the apothem.s is the side length of the polygonn is the number of sides of the polygonNow, substitute the values, we have;
a = 8/2tan(180/9)
divide the values
a = 8/2tan 20
Find the values
a = 8/0. 7279
Divide the values
a = 10. 99cm
Learn more about polygons at: https://brainly.com/question/8409681
#SPJ1
Solve -2a -5 > 3 Which graph shows the solutions?

Answers
Answer: a< -4 D
Step-by-step explanation:
Consider versus A random sample of 35 observations taken from this population produced a sample mean of 40.27. The population is normally distributed with Calculate the p-value. Round your answer to four decimal places.
Answers
Complete Question
Consider H0: μ=38 versus H1: μ>38. A random sample of 35 observations taken from this population produced a sample mean of 40.27. The population is normally distributed with σ=7.2.
Calculate the p-value. Round your answer to four decimal places.
Answer:
The \(p-value = 0.030742\)
Step-by-step explanation:
From the question we are told that
The population mean is \(\mu = 38\)
The sample size is n = 35
The sample mean is \(\= x = 40.27\)
The standard deviation is \(\sigma = 7.2\)
The null hypothesis is \(H_o\): μ=38
The alternative hypothesis is H1: μ>38
Generally the test statistics is mathematically represented as
\(t = \frac{ \= x -\mu }{\frac{\sigma }{ \sqrt{n} } }\)
=> \(t = \frac{ 40.27 - 38 }{\frac{ 7.2 }{ \sqrt{ 35} } }\)
=> \(t =1.87\)
Generally from the z table the p-value of \((Z > 1.87 )\) is
\(p-value = P(Z > 1.87) = 0.030742\)
When Lisa started at her current job, her employer gave her 3 days of paid vacation time with a promise of 2 additional paid vacation days each additional year she remains with the company to a maximum of 20 days of paid vacation time. It has been 5 years since Lisa began working for this employer. How many paid vacation days has she earned?
Answers
Answer:
13 days
Step-by-step explanation:
She starts with 3
She gets 2 for each year with the company
She has been their 5 years
5*2 = 10
10+3 = 13
The total number of paid vacation days after working for 5 years is 13 days.
Linear EquationThe equation having the highest power of its variable as 1 is called a linear equation.
How to form a linear equation based on given situations?Let the total number of paid vacations be y.
And the number of years Lisa worked for the company be x.
The fixed paid vacation is for 3 days.
The number of additional paid vacation days for each additional year is 2 days.
So, the linear equation formed is,
y = 2x + 3 ... (i)
How many paid vacation days has she earned after 5 years?Put the value of x = 5 in the equation (i),
y = 2(5) + 3
y = 10 + 3
y = 13
Hence, the number of paid vacation days earned by Lisa after 5 years of working is 13 days.
Learn more about linear equations here - https://brainly.com/question/17449824
#SPJ2
Stephanie is making 1 1/2 batches of cookies using 2 3/4 cup sugar. How much sugar total?()
Answers
Answer:
33/8 or 4 1/8 simplified.
Match each of the expression in column 1 with an equivalent expression in column 2
Answers

Is this correct?
Thank you!

Answers
Answer:
yes .it is totally correct
if you don’t know for sure don’t answer lol this is a test so I don’t wanna get anything wrong

Answers
Answer:
C. x = 1/2
Step-by-step explanation:
To find x, simply take the cube root of the cube's given volume. with a volume of 1/8 cubic centimetres, (this is an assumption, as the question expresses the volume in square centimetres, which is not a valid unite of volume; presumably that's a typo), the side length will be:
√(1/8)
= √1 / √8
= 1 / 2
So x is equal to 1/2 of a centimetre.
Answer:
x= 1/2
Step-by-step explanation:
The formula to find the volume of a cube is \(a^3\), we can work backwards with the volume to find the edges:
\(1/8=x^3\\\sqrt[3]{1/8} =x\\1/2=x\)
HELPPP PLEASEEE! I tried everything from adding to dividing, subtracting, multiplying but still no correct answer. Can someone help me out here please? I am not sure where to start either now. Thank you for your time.

Answers
You have some data points labeled by \(x\). They form the set {3, 5, 7}.
The mean, \(\bar x\), is the average of these values:
\(\bar x = \dfrac{3+5+7}3 = \dfrac{15}3 = 5\)
Then in the column labeled \(x-\bar x\), what you're doing is computing the difference between each data point \(x\) and the mean \(\bar x\):
\(x=3 \implies x-\bar x = 3 - 5 = -2\)
\(x=5 \implies x-\bar x = 5-5 = 0\)
\(x=7 \implies x-\bar x = 7 - 5 = 2\)
These are sometimes called "residuals".
In the next column, you square these values:
\(x=3 \implies (x-\bar x)^2 = (-2)^2 = 4\)
\(x=5 \implies (x-\bar x)^2 = 0^2 = 0\)
\(x=7 \implies (x-\bar x)^2 = 2^2 = 4\)
and the variance of the data is the sum of these so-called "squared residuals".
(1 1 6 − 7 18 )÷2.8 0.5+ 1 18
Answers
Step-by-step explanation:
(116-718) /(2.805+118) [as, there cannot be two decimals in one numbers
=-602/120.805
=0.498
Pls help
Me i have alot and this is due tomorrow

Answers
8,8,8,8, 9 ,10,12,12,14
9err9jwihwr9ihwrighiwrrghihsrhrgishfgisif10101
Answers
Answer:
yes
Step-by-step explanation:
...
The profit that a company makes selling an item (in thousands of dollars) depends on the price of the item (in dollars). If p is the price of the item, then f(p) = −2p² + 24p – 54, then what are the prices that give a profit of zero dol
lars?
Answers
The solution is, the profit is 18.
If the profit of a company made by the company is in the form a quadratic expressions but in the different forms as given in the question.
a). The prices that give a profit of zero dollars.
Expression that is most useful,
Factored form: -2(p - 3)(p - 9) = 0
p = 3, 9
b). The profit when the price is zero .
Standard form:
Profit = -2p² + 24p - 54 = 0
-p² + 12p - 27 = 0
-p² + 3p + 9p - 27 = 0
-p(p - 3) + 9(p -3) = 0
(-p + 9)(p - 3) = 0
p = 3, 9
c). The price that gives the maximum profit.
Vertex form: -2(p - 6)² + 18
Vertex of the given expression → (6, 18)
Maximum profit will be at p = 6.
Therefore, profit = -2(6 - 6)² + 18 = 18
Learn more about Profit here
brainly.com/question/19161495
#SPJ1
complete question:
The profit that a company makes selling an item (in thousands of dollars) depends on the price of the item (in dollars). If p is the price of the item, then three equivalent forms for the profit are
Standard form: - 2 p^2 + 24p - 54
Factored form: -2(p - 3)(y-9)
Vertex form: -2(p-6)^2 + 18.
Which form is most useful for finding a. The prices that give a profit of zero dollars?
b. The profit when the price is zero?
c. The price that gives the maximum profit?
Write 3 1/2 cups as a multiplication expression using the unit, 1 cup, as a factor.
I ABSOLUTELY NEED HELP BY TOMORROW!!! I AM GIVING 100 POINTS

Answers
3 1/2 cups can be expressed as the multiplication expression: 3 + 1/2.
How to Write 3 1/2 cups as a multiplication expression using the unit, 1 cup, as a factor.To express 3 1/2 cups as a multiplication expression using the unit "1 cup" as a factor, you can write it as:
3 1/2 cups = (3 + 1/2) cups = 3 cups + 1/2 cup
Since there are 1 cup in each term, we can rewrite it as:
3 cups + (1/2) cup
Now, we can express each term as a multiplication expression:
3 cups = 3 * 1 cup = 3
(1/2) cup = (1/2) * 1 cup = 1/2
Putting it all together, the multiplication expression is:
3 * 1 cup + (1/2) * 1 cup = 3 + 1/2
Therefore, 3 1/2 cups can be expressed as the multiplication expression: 3 + 1/2.
Learn more about expression at https://brainly.com/question/1859113
#SPJ1
Huuuurrry plllzzzzzz. Determine the equation of the line that passes through the given points (2,6) and (4,16)
Answers
Linear equations are typically organized in slope-intercept form:
\(y=mx+b\)
m is the slope of the lineb is the y-intercept (the value of y when the line passes through the y-axis)To find linear equations in slope-intercept form:
Determine the slopePlug the slope into the general formDetermine the y-intercept by isolating bPlug the b back into the equationSolving the QuestionWe're given:
The line passes through the points (2,6) and (4,16)First, determine the slope of the line.
\(m=\dfrac{y_2-y_1}{x_2-x_1}\) where \((x_1,y_1)\) and \((x_2,y_2)\) are points that fall on the line
⇒ Plug in the given points (2,6) and (4,16):
\(m=\dfrac{16-6}{4-2}\\\\m=\dfrac{10}{2}\\\\m=5\)
⇒ Therefore, the slope of the line is 5. Plug this back into the general form:
\(y=5x+b\)
Now, determine the y-intercept.
\(y=5x+b\)
⇒ Plug in one of the given points:
\(6=5(2)+b\\6=10+b\\b=-4\)
⇒ Therefore, the y-intercept is -4. Plug this back into our original equation:
\(y=5x-4\)
Answer\(y=5x-4\)
8y-5< 3
Solve the inequality. The solution is _____.
Answers
Answer:
Use Photo Math, it will explain all of the steps
Pleaseeeeeee HELP!!!!!!
A piece of farm machinery clears 2/15 acre of land in 1/5 of an hour

Answers
Answer: D. 2/3
Step-by-step explanation:
If it is 1/5 of an hour, we times it by 5, to get full hour, right?
So, we also do ×5 for the acre of land, so we can get the amount of acres in a full 1 hour.
5 is the same as 5/1 as a fraction
1/5 × 5 = 5/5 ......1 hour
2/15 × 5/1 = 10/15
So we get, 10/15 acre of land cleared in 1 hour
We simplify 10/15,
Which becomes,
2/3.
In conclusion, this is the working out =
2/15 × 5 = 10/15 = 2/3
Mark my answer as the brainliest!WILL GIVE BRAINLIEST

Answers
Answer:
C
Step-by-step explanation:
It's not A and B because an exponent to the negative number leads to the fraction.
e.g. 10^-a = 1/(10^a)
It's not D because 5,030,000 rounds to 5,000,000 and not 6,000,000.
Hurry in test Brainliest!!!

Answers
Answer:
y = (x - 4) - 4
Step-by-step explanation:
m = \(\frac{y_{2} - y_{1} }{x_{2} -x_{1} }\)
(- 2, - 10)
(4 , - 4)
m = \(\frac{-4+10}{4+2}\) = 1
y + 4 = (x - 4) ⇒ y = (x - 4) - 4
I want to know how to do 11/13+44/39
Answers
Answer:
I'm pretty sure that the answer is 1.97
\( \frac{11}{13} + \frac{44}{39} \)
11/13 ×3
11×3=33
13×3=39
11/13=33/39
33/39+44/39
= 77/39
77÷39
=
\(1 \frac{38}{39} \)
I need quick help! I just want know if this is correct! Will give brainliest to the first correct answer.

Answers
Parallel: equation with slope 1/4
Perpendicular: equation with slope -4
Neither: equation with slope 4
You need to solve a system of equations. You decide to use the elimination method. Which of these is not allowed? 2x-3y=12 Equation 1 -2x+y=8 Equation 2 A. Add equation 2 to equation 1. B. Multiply equation 2 by 3. Then subtract the result from equation 1. C. Add the left side of equation 2 to the left side of equation 1.
Answers
Multiply equation 2 by 3. Then subtract the result from equation 1.
Explanation:
The 2nd equation given to us is -2x+y = 8
Triple both sides to get -6x+3y = 24
This means the original system
\(\begin{cases}2x-3y = 12\\-2x+y = 8\end{cases}\)
is equivalent to
\(\begin{cases}2x-3y = 12\\-6x+3y = 24\end{cases}\)
If we were to add the equations, then the y terms would cancel out because -3y+3y = 0y = 0.
Subtracting the equations will not cancel out the y terms.
-3y minus 3y = -3y -3y = -6y
Therefore the portion saying "Then subtract the result from equation 1." in answer choice B is not correct. It should be "add the equations" or "add the result to equation 1" after tripling both sides of the 2nd equation.
Answer choices A and C say the same thing more or less. Adding the original equations straight down will cancel out the x terms. Therefore, choices A and C are valid approaches to using elimination. We can cross choices A and C off the list.
Suppose that $16,065 is invested at an interest rate of 6.6% per year, compounded continuously. a) Find the exponential function that describes the amount in the account after time t, in years. b) What is the balance after 1 year? 2 years?5 years? 10 years? c) What is the doubling time?

Answers
Okay, here we have this:
Considering the provided information we obtain the following:
a)
Replacing in the Compound Interest formula we obtain the following:
\(\begin{gathered} A(t)=Pe^{rt} \\ A(t)=16065e^{0.066t} \end{gathered}\)b)
After 1 year (t=1):
\(\begin{gathered} A(1)=16065e^{0.066(1)} \\ A(1)\approx17,161.06 \end{gathered}\)We obtain that after one year the balance is aproximately $17,161.06.
After 2 years (t=2):
\(\begin{gathered} A(2)=16065e^{0.066(2)} \\ A(2)=18331.90 \end{gathered}\)We obtain that after two years the balance is aproximately $18,331.90
After 5 years (t=5):
\(\begin{gathered} A(5)=16065e^{0.066(5)} \\ A(5)=$22,345.90$ \end{gathered}\)We obtain that after five years the balance is aproximately $22,345.90.
After 10 years (t=10):
\(\begin{gathered} A(10)=16065e^{0.066(10)} \\ A(10)=$31,082.44$ \end{gathered}\)We obtain that after ten years the balance is aproximately $31,082.44.
c)
In this case the doubling time will be when she has double what she initially had, that is: $16,065*2=$32130, replacing in the formula:
\(32130=16065e^{0.066t}\)Let's solve for t:
\(\begin{gathered} 32130=16065e^{0.066t} \\ 16065e^{\mleft\{0.066t\mright\}}=32130 \\ \frac{16065e^{0.066t}}{16065}=\frac{32130}{16065} \\ e^{\mleft\{0.066t\mright\}}=2 \\ 0.066t=\ln \mleft(2\mright) \\ t=\frac{\ln\left(2\right)}{0.066} \\ t\approx10.502years \end{gathered}\)Finally we obtain that the doubling time is approximately 10.502 years or about 10 years 6 months.
Christopher Columbus set sail from Spain in 1492. In what year did the Civil War end?
Font Sizes
Answers
Answer:
May 9, 1865
Step-by-step explanation:
Determine whether the point is on the graph of the equation 2x+7y=13
(-4,3)
Is (-4,3) on the graph of 2x+7y=13?
Yes or no?

Answers
Answer:
(I) yessssssssssssssssssssssss
Answer:
yes it is.
Step-by-step explanation:
i did this and it was correct
Consider the polynomial: StartFraction x Over 4 EndFraction – 2x5 + StartFraction x cubed Over 2 EndFraction + 1 Which polynomial represents the standard form of the original polynomial? StartFraction x cubed Over 2 EndFraction – 2x5 + StartFraction x Over 4 EndFraction + 1 –2x5 + StartFraction x cubed Over 2 EndFraction + StartFraction x Over 4 EndFraction + 1 –2x5 + StartFraction x Over 4 EndFraction + StartFraction x cubed Over 2 EndFraction + 1 1 – 2x5 + StartFraction x cubed Over 2 EndFraction + StartFraction x Over 4 EndFraction
Answers
Answer:
(B)\(-2x^5+\dfrac{x^3}{2}+\dfrac{x}{4}+1\)
–2x5 + StartFraction x cubed Over 2 EndFraction + StartFraction x Over 4 EndFraction + 1
Step-by-step explanation:
Given the polynomial: \(\dfrac{x}{4}-2x^5+\dfrac{x^3}{2}+1\)
We are required to pick an equivalent polynomial which is in standard form.
A polynomial is in standard form when it is written in descending powers of x.
Therefore, rearranging the polynomial above, we have:
\(-2x^5+\dfrac{x^3}{2}+\dfrac{x}{4}+1\)
The correct option is B.
The correct answer is B. –2x5 + StartFraction x cubed Over 2 EndFraction + StartFraction x Over 4 EndFraction + 1
hope you have a great day :D
divide 7 by 12 to change 7/12 to a repeating decimal. 7/12 = 7 divided by 12 = ?
Answers
Answer:
0.58333333....
can i have brainliest plz
100 Points! Geometry question. Photo attached. Please show as much work as possible. Thank you!

Answers
Answer:
\(BC=5.1\)
\(B=23^{\circ}\)
\(C=116^{\circ}\)
Step-by-step explanation:
The diagram shows triangle ABC, with two side measures and the included angle.
To find the measure of the third side, we can use the Law of Cosines.
\(\boxed{\begin{minipage}{6 cm}\underline{Law of Cosines} \\\\$c^2=a^2+b^2-2ab \cos C$\\\\where:\\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides.\\ \phantom{ww}$\bullet$ $C$ is the angle opposite side $c$. \\\end{minipage}}\)
In this case, A is the angle, and BC is the side opposite angle A, so:
\(BC^2=AB^2+AC^2-2(AB)(AC) \cos A\)
Substitute the given side lengths and angle in the formula, and solve for BC:
\(BC^2=7^2+3^2-2(7)(3) \cos 41^{\circ}\)
\(BC^2=49+9-2(7)(3) \cos 41^{\circ}\)
\(BC^2=49+9-42\cos 41^{\circ}\)
\(BC^2=58-42\cos 41^{\circ}\)
\(BC=\sqrt{58-42\cos 41^{\circ}}\)
\(BC=5.12856682...\)
\(BC=5.1\; \sf (nearest\;tenth)\)
Now we have the length of all three sides of the triangle and one of the interior angles, we can use the Law of Sines to find the measures of angles B and C.
\(\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} $\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}\)
In this case, side BC is opposite angle A, side AC is opposite angle B, and side AB is opposite angle C. Therefore:
\(\dfrac{\sin A}{BC}=\dfrac{\sin B}{AC}=\dfrac{\sin C}{AB}\)
Substitute the values of the sides and angle A into the formula and solve for the remaining angles.
\(\dfrac{\sin 41^{\circ}}{5.12856682...}=\dfrac{\sin B}{3}=\dfrac{\sin C}{7}\)
Therefore:
\(\dfrac{\sin B}{3}=\dfrac{\sin 41^{\circ}}{5.12856682...}\)
\(\sin B=\dfrac{3\sin 41^{\circ}}{5.12856682...}\)
\(B=\sin^{-1}\left(\dfrac{3\sin 41^{\circ}}{5.12856682...}\right)\)
\(B=22.5672442...^{\circ}\)
\(B=23^{\circ}\)
From the diagram, we can see that angle C is obtuse (it measures more than 90° but less than 180°). Therefore, we need to use sin(180° - C):
\(\dfrac{\sin (180^{\circ}-C)}{7}=\dfrac{\sin 41^{\circ}}{5.12856682...}\)
\(\sin (180^{\circ}-C)=\dfrac{7\sin 41^{\circ}}{5.12856682...}\)
\(180^{\circ}-C=\sin^{-1}\left(\dfrac{7\sin 41^{\circ}}{5.12856682...}\right)\)
\(180^{\circ}-C=63.5672442...^{\circ}\)
\(C=180^{\circ}-63.5672442...^{\circ}\)
\(C=116.432755...^{\circ}\)
\(C=116^{\circ}\)
\(\hrulefill\)
Additional notes:
I have used the exact measure of side BC in my calculations for angles B and C. However, the results will be the same (when rounded to the nearest degree), if you use the rounded measure of BC in your angle calculations.
What is the answer to this
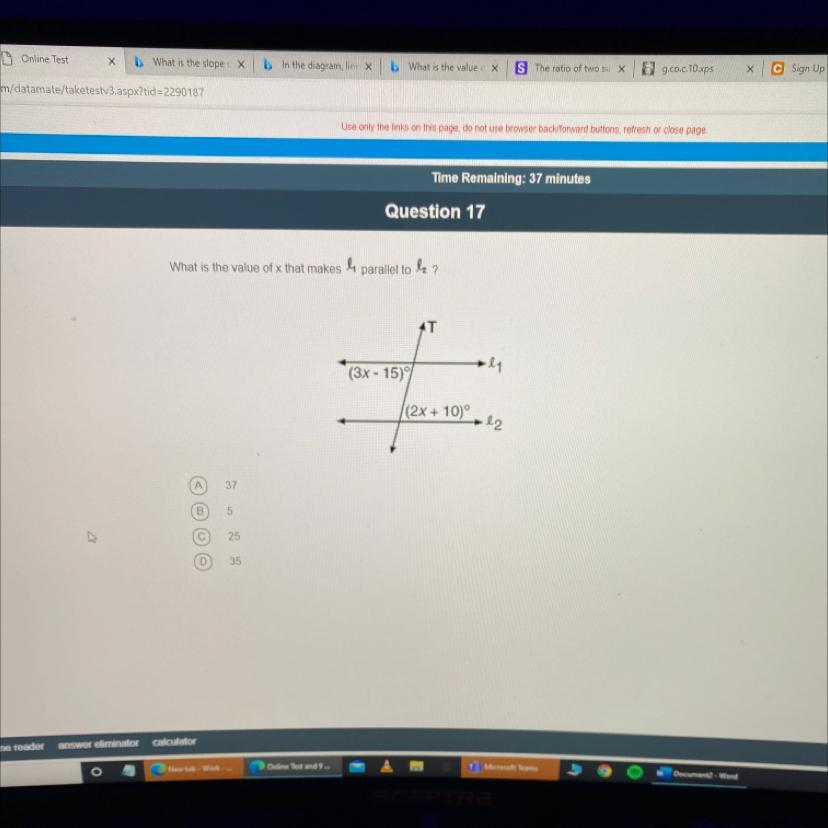
Answers
Answer:
x = 25
Step-by-step explanation:
3x-15 = 2x+10
x-15 = 10
x = 25
Answer:
x = 25 degree
Step-by-step explanation:
3x - 15 = 2x + 10 (their relation will be alternate interior angles if they \(l_{1}\) and \(l_{2}\) are parallel)
3x - 2x = 10 + 15
x = 25 degree