Find the slope of a line perpendicular to the line whose equation is 4x-3y=-3
Answers
The slope of a line perpendicular to the line whose equation is 4x-3y=-3 is -3/4.
We have Equation
4x- 3y= -3
Writing the above equation in the from of slope intercept form
3y= 4x + 3
y= 4/3 x + 1
Here the slope of line is 4/3.
As, the slope of perpendicular line have product -1.
let the slope of perpendicular line is m.
So, m x 4/3 = -1
x = -3/4
Thus, the slope perpendicular line is -3/4.
Learn more about Slope here:
https://brainly.com/question/3605446
#SPJ1
Related Questions
Find an equation of the line described below. Write the equation in slope intercept form( solved for y) when possible through (8,5) and (5,8)
Answers
\((\stackrel{x_1}{8}~,~\stackrel{y_1}{5})\qquad (\stackrel{x_2}{5}~,~\stackrel{y_2}{8}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{5}}}{\underset{\textit{\large run}} {\underset{x_2}{5}-\underset{x_1}{8}}} \implies \cfrac{ 3 }{ -3 } \implies - 1\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{5}=\stackrel{m}{- 1}(x-\stackrel{x_1}{8}) \\\\\\ y-5=-x+8\implies {\Large \begin{array}{llll} y=-x+13 \end{array}}\)
Answer ASAP but only if you are SURE about it
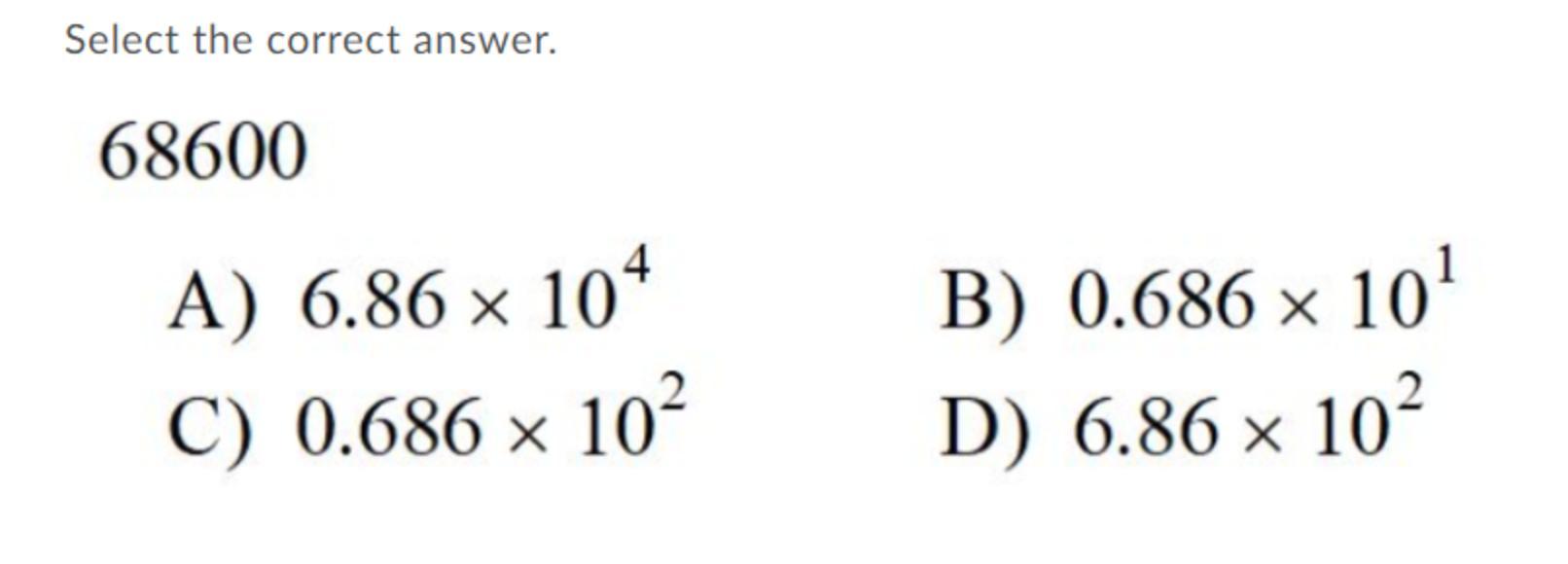
Answers
Answer:
It's A, 6.86 × 10⁴
Step-by-step explanation:
In scientific notation, you have the base, and the 10. The 10 is represented next to an exponent, whereas the base is a whole number and a decimal. If the decimal is moved right, the exponent following the 10 becomes negative. Left, it becomes positive. In this instance, the decimal is being moved left, thus the exponent is positive.
Answer:
A
Step-by-step explanation:
All my work is provided in the attached Screenshot! :)

Give the name of the parent function of y = 2[x-5]
Answers
The parent function of the transformed function is y = f ( x ) = x
Given data ,
Let the parent function be represented as f ( x )
Now , the value of f ( x ) is
The transformed function is represented as y
where y = 2 ( x - 5 )
On simplifying , we get
y = 2( x - 10 )
If the original function is y = f(x), assuming the horizontal axis is the input axis and the vertical is for outputs, then:
The function is shifted horizontally left by 10 units and multiplied by a scale factor of 2 units.
Hence , the parent function is f ( x ) = x
To learn more about transformation of functions click :
https://brainly.com/question/26896273
#SPJ1
Is this an angle of elevation or angle of depression problem? Solve for x.

Answers
The angle is the angle of depression.
The solution is x = 130.54 approximately.
The angle suggests the view from top to bottom so the angle is called the angle of depression.
It is a right angled triangle with hypotenuse x and base 100 ft.
And the angle of depression is \(=40^\circ\).
By the condition,
\(\cos40^\circ =\frac{100}{x}\Rightarrow x=\frac{100}{\cos40^\circ}\approx130.54\) ft.
Hence the solution of x or the length of hypotenuse is 130.54 ft.
To know more about Hypotenuse refer to:
https://brainly.com/question/2217700
#SPJ9
The ski team needs new uniforms. The students plan to sell plush toy eagles (the school mascot) for $5 each. The students find three companies on-line that sell stuffed mascots. Company A sells 18 eagles for $49.32. Company B sells 16 eagles for $43.36. Company C charges $41.55 for 15 eagles. Which company has the best buy?
Answers
Answer:
i think b im not sure but i think
Answer:
Company B
Step-by-step explanation:
A. 18e = 49.32 e = 2.74
B. 16e = 43.36 e = 2.71
C. 15e = 41.55 e = 2.77
You need to borrow $2550 to help contribute to an upcoming family reunion. You can borrow the money from two different banks.
Bank A will lend you $2550 for six months at an interest rate of 11.5%
How much money will you owe at the end of each period of time? Which bank offer will you choose and why?
Bank B will lend you $2550 for twelve months at an interest rate of 7.5%
Answers
Amount to be repaid for Bank A is $2,696.625 and Amount to be repaid for Bank B is $2,741.25. However, I will choose Bank B because it offers a lower interest rate.
How to calculate the simple interest?The formula to calculate the simple interest is;
I = PRT
Where;
P is principal
R is rate
T is time
Now, we are given that;
Bank A;
Principal amount; P = $2550
Interest rate; R = 11.5% = 0.115
Time; t = 6 months = 0.5 years
Thus;
I = (2550 * 0.115 * 0.5)
I = $146.625
Amount to be repaid = 2550 + 146.625
Amount to be repaid = $2,696.625
Bank B;
Principal amount; P = $2550
Interest rate; R = 7.5% = 0.075
Time; t = 12 months = 1 year
Thus;
I = (2550 * 0.075 * 1)
I = $191.25
Amount to be repaid = 2550 + 191.25 = $2,741.25
Thus, bank B offers a more favorable interest rate and as such would be the preferred bank.
Read more about simple interest at; https://brainly.com/question/20690803
#SPJ1
Translate the following into a math expression:
twenty less than the product of five and a number
A: (x+5) - 20
B: 20-5x
C: 5x-20
D: 5/x - 20
Answers
Answer:
\(5x - 20\)
Step-by-step explanation:
Product means the result of the multiplication of two numbers. A part of our expression will include the product of five and a number. We don't know what number it is, therefore, we'll call it \(x\). The product of those two numbers can be algebraically expressed as \(5x\) (we usually eliminate the multiplication sign between numbers and variables).
We are then asked to express the number that is 20 less than the product we found earlier. To find this expression, we should subtract 20 from the product, giving us \(5x - 20\).
I need help plz someone help me solved this problem I need help ASAP! I will mark you as brainiest!

Answers
Step-by-step explanation:
P= R - C = -0,5x^2 + 70x -2100= 300
P=-0,5x^2 +70x -2400=-0,5(x^2 -140x +4800)=-0,5(x^2- 80x -60x +4800)=-0,5(x-60)(x-80)=0
so x =60 or x=80
Answer:
Total cost is 123 items selled
Evaluate please
\( - ({2}^{6})( {2}^{3)} \)
Answers
Step-by-step explanation:
\( - ({2}^{6})( {2}^{3)} \\ \\ = - {2}^{6 + 3} \\ \\ = - {2}^{9} \)
Which function has a greater maximum?
�
(
�
)
=
−
2
(
�
+
4
)
2
+
1
f(x)=−2(x+4)
2
+1f, left parenthesis, x, right parenthesis, equals, minus, 2, left parenthesis, x, plus, 4, right parenthesis, squared, plus, 1
A coordinate plane. The x- and y-axes both scale by one. The graph is the function y equals g of x which is a parabola that opens down. The function increases through negative four, negative five and negative three, negative two. It has a maximum at negative two, one, then the function decreases through negative one, negative two and zero, negative five.
Answers
The function f(x) = \(-2(x+4)^2\) + 1 has a greater maximum.
1. The given function is f(x) = \(-2(x+4)^2\) + 1.
2. To find the maximum of the function, we need to determine the vertex of the parabola.
3. The vertex form of a quadratic function is given by f(x) = \(a(x-h)^2\) + k, where (h, k) represents the vertex.
4. Comparing the given function to the vertex form, we see that a = -2, h = -4, and k = 1.
5. The x-coordinate of the vertex is given by h = -4.
6. To find the y-coordinate of the vertex, substitute the x-coordinate into the function: f(-4) = \(-2(-4+4)^2\) + 1 = \(-2(0)^2\) + 1 = 1.
7. Therefore, the vertex of the function is (-4, 1), which represents the maximum point.
8. Comparing this maximum point to the information provided about the other function g(x) on the coordinate plane, we can conclude that the maximum of f(x) = \(-2(x+4)^2\) + 1 is greater than the maximum of g(x).
9. The given information about g(x) is not sufficient to determine its maximum value or specific equation, so a direct comparison is not possible.
10. Hence, the function f(x) =\(-2(x+4)^2\) + 1 has a greater maximum.
For more such questions on maximum, click on:
https://brainly.com/question/29795588
#SPJ8
What is the first step in evaluating the expression shown below?
12
÷
(
7
.
4
−
3
.
6
)
+
8
−
2
Answers
Answer:
Step-by-step explanation:
The first step in evaluating the expression is to perform the calculations inside the parentheses. This involves subtracting 3.6 from 7.4.
Step 1: Evaluate the expression inside the parentheses.
7.4 - 3.6 = 3.8
After evaluating the expression inside the parentheses, the expression becomes:
12 ÷ 3.8 + 8 - 2
Step 2: Perform the division.
12 ÷ 3.8 = 3.158
After performing the division, the expression becomes:
3.158 + 8 - 2
Step 3: Perform the addition and subtraction from left to right.
3.158 + 8 = 11.158
11.158 - 2 = 9.158
Therefore, the value of the given expression is approximately 9.158.
The first step is:
⇨ parenthesesWork/explanation:
The expression is:
12 ÷ (7.4 − 3.6) + 8 − 2
Let's recall the order of operations first:
order of operations = PEMDASPEMDASParenthesesExponentsMultiplicationDivisionAdditionSubtractionSo we evaluate
\(\sf{12\div(7.4-3.6)+8-2}\)
\(\sf{12\div3.8+8-2}\)
Next, division:
\(\sf{3.158+8-2}\)
Next, addition & subtraction:
\(\sf{9.158}\)
Hence, the first step is to evaluate the parentheses.Part a:Cell phone usage grew about 23% each year from 2010 to 2016. If cell phone usage in 2010 was 43 million, write a function f(x) to model U.S. cell phone usage over that time period, where x is the number of years since 2010.
Part b estimate the cell phone usage in 2013.round to the nearest ten thousand.
Answers
Answer:
The function f(x) to model U. S. cell phone usage over the time period of 2010 to 2016 can be expressed as f(x) = 43 * (1.23^x), where x is the number of years since 2010. Part b: The estimated cell phone usage in 2013 can be calculated by substituting x = 3 into the function f(x) = 43 * (1.23^x). This yields an estimated cell phone usage of 68.4 million in 2013, which can be rounded to the nearest ten thousand to 68 million.
Step-by-step explanation:
Is this right? Pls help

Answers
Answer:
A
Step-by-step explanation:
DE is the shortest side because it's is opposite to the smallest angle (<F)
180 - 60 = 3X +2X + 5,
X = 23
<F = 2*(23) +5 = 51
A diphosphonate kit contian 180 mCi of Tc99m in 30 ml when it is prepared at 8am. Immediately, a 20 mCi dose is withdrawn for a bone scan. if the patient arrives late at 9:30 and half the volume is accidentally discharged, how much volume from the kit must now be added to the syringe to correct the dose to 20 mCi? (no other doses have been withdrawn meanwhile, and the decay factor for 1.5 hrs is 0.841)
Answers
The remaining Kit volume in the syringe is sufficient to correct the dose to 20 mCi.
To solve this problem, we can use the concept of radioactive decay and the decay factor. Here's how we can calculate the required volume to correct the dose:
Determine the initial activity of the kit:
Initial activity = 180 mCi
Calculate the decayed activity at 9:30 (after 1.5 hours):
Decay factor = 0.841
Decay activity = Initial activity * Decay factor
Calculate the remaining activity after withdrawing 20 mCi at 8 am:
Remaining activity = Initial activity - 20 mCi
Calculate the remaining activity at 9:30:
Remaining activity at 9:30 = Remaining activity * Decay factor
Calculate the desired activity at 9:30 (20 mCi):
Desired activity at 9:30 = 20 mCi
Calculate the volume needed to achieve the desired activity:
Volume needed = Desired activity at 9:30 / Remaining activity at 9:30 * Volume at 9:30
Calculate the remaining volume at 9:30:
Remaining volume = Volume at 8 am - Volume withdrawn - Volume accidentally discharged
Calculate the volume that needs to be added:
Volume to be added = Volume needed - Remaining volume
Let's perform the calculations step by step:
Determine the initial activity of the kit:
Initial activity = 180 mCi
Calculate the decayed activity at 9:30 (after 1.5 hours):
Decay factor = 0.841
Decay activity = 180 mCi * 0.841 = 151.38 mCi
Calculate the remaining activity after withdrawing 20 mCi at 8 am:
Remaining activity = 180 mCi - 20 mCi = 160 mCi
Calculate the remaining activity at 9:30:
Remaining activity at 9:30 = 160 mCi * 0.841 = 134.56 mCi
Calculate the desired activity at 9:30 (20 mCi):
Desired activity at 9:30 = 20 mCi
Calculate the volume needed to achieve the desired activity:
Volume needed = (Desired activity at 9:30 / Remaining activity at 9:30) * Volume at 9:30
Volume at 9:30 = Remaining volume = 30 ml - (30 ml / 2) = 15 ml
Volume needed = (20 mCi / 134.56 mCi) * 15 ml = 2.236 ml
Calculate the remaining volume at 9:30:
Remaining volume = 30 ml - (30 ml / 2) = 15 ml
Calculate the volume that needs to be added:
Volume to be added = Volume needed - Remaining volume = 2.236 ml - 15 ml = -12.764 ml
Since the calculated volume to be added is negative, it means that no additional volume is required. The remaining Kit volume in the syringe is sufficient to correct the dose to 20 mCi.
For such more questions on Kit Volume Correction
https://brainly.com/question/22971212
#SPJ8
A computer chooses a number at random from a list of 6 different positive, single-digit numbers. The probabilities of different events are shown below in the table below. Use this information to find the 6 numbers the computer is choosing from.


Answers
The 6 numbers for the given probabilities can be:
(2, 4, 5, 6, 7, 8)
How to find the numbers?There are 6 numbers, we know that:
probability of any event = (outcomes that meet the event)/6
Then, if:
probability of an even number = 2/3 = 4/6
This means that there are 4 even numbers.
if:
P Number chosen is less than 5 = 1/3 = 2/6
There are 2 numbers less than 6.
And there is a 50% of gettting a prime, so there are two primes.
Then the 6 numbers could be:
(2, 4, 5, 6, 7, 8)
There are 4 even numbers {2, 4, 6, 8}Two primes {2, 7}Two smaller than 5 { 2, 4}Learn more about probability at.
https://brainly.com/question/25870256
#SPJ1
Which is the correct value of Z for the solution to true system?
2x+3y-z=4
x-3y+2z=-3
3x+y-z=5

Answers
The correct value of Z for the solution to true system is -2
How to determine the correct value of Z for the solution to true system?From the question, we have the following parameters that can be used in our computation:
2x + 3y - z = 4
x - 3y + 2z = -3
3x + y - z = 5
Transform the third equation
So we have
2x + 3y - z = 4
x - 3y + 2z = -3
9x + 3y - 3z = 15
Eliminate y in the equations by subtraction
So we have
x - 3z = 7
10x - z = 12
Multiply x - 3z = 7 by 10
10x - 30z = 70
10x - z = 12
Subtract the equations
-29z = 58
So, we have
z = -2
Hence, the correct value of Z is -2
Read more about equations at
https://brainly.com/question/148035
#SPJ1
If the production function is given by : Q = 4L +3L² +7L3 solve the following questions. then find marginal production function (MP). find marginal product when unit of labour is 6.
Answers
When the unit of labor is 6, the marginal product is 796.
The marginal production function (MP) can be obtained by taking the derivative of the production function with respect to labor (L). In this case, the production function is Q = 4L + 3L² + 7L³. Taking the derivative of this equation with respect to L will give us the marginal production function.
The derivative of the production function with respect to L is MP = 4 + 6L + 21L².
To find the marginal product when the unit of labor is 6, we substitute L = 6 into the marginal production function:
MP = 4 + 6(6) + 21(6)²
= 4 + 36 + 21(36)
= 4 + 36 + 756
= 796.
In summary, the marginal production function is MP = 4 + 6L + 21L², and the marginal product when the unit of labor is 6 is 796. The marginal production function represents the additional output produced when one additional unit of labor is employed.
In this case, the marginal production function is a quadratic function with positive coefficients, indicating increasing returns to scale. The marginal product of labor represents the change in output resulting from a one-unit increase in labor input, given the level of other inputs.
When the unit of labor is 6, the marginal product is found by substituting L = 6 into the marginal production function, resulting in a value of 796. This means that when the firm employs an additional unit of labor (6th unit), the output increases by 796 units.
for such more questions on marginal
https://brainly.com/question/6450400
#SPJ8
Evaluate the following expression.
(-3)0
Answer here
Answers
The expression (-3)0 has a value of 0 when evaluated because a number multiplied by 0 gives 0
Evaluating the expression (-3)0From the question, we have the following parameters that can be used in our computation:
(-3)0
The above statement is a product expression that multiplies the values of -3 and 0
Also, there is no need to check if there are like terms in the expression or not
This is because we are multiplying the factors
So, we have
(-3)0 = 0
This means that the value of the expression is 0 i.e a number multiplied by 0 gives 0
Read more about expression at
brainly.com/question/15775046
#SPJ1
Solve for 44.
4 4 = [?]
510
51
44/42
![Solve for 44.4 4 = [?]5105144/42](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/GAy97egcxMke22LIgjim4JhPTNNGBIPA.png)
Answers
Angle 4 is an exterior angle which is equal to the sum of the two opposite inside angles.
The two opposite inside angles are given as 51 and 51
Angle 3 = 51 + 51 = 102 degrees.
Answer:
\( \displaystyle \angle4 = {108}^{ \circ} \)
Step-by-step explanation:
the sum of the interior angles of a triangle is 180°
thus our equation is
\( \displaystyle {51}^{ \circ} + {51}^{ \circ} + \angle2 = {180}^{ \circ} \)
simplify addition:
\( \displaystyle {102}^{ \circ} + \angle2 = {180}^{ \circ} \)
cancel 102° from both sides:
\( \displaystyle \angle2 = {72}^{ \circ} \cdots \text{I}\)
By straight line theorem we acquire:
\( \displaystyle \angle4 + \angle2 = {180}^{ \circ} \)
substitute:
\( \displaystyle \angle4 + {72}^{ \circ} = {180}^{ \circ} \)
cancel 72° from both sides:
\( \displaystyle \angle4 = {108}^{ \circ} \)
hence, the measure of \(\angle 4\) is 108°
please help. Thank you

Answers
Answer:
30.8 degrees
Step-by-step explanation:
cosx = \(\frac{8.5}{9.9}\)
x= \(cos^{-1}\)\(\frac{8.5}{9.9}\)
= 30.8 degrees (nearest tenth of a degree)
Status
Recovery
ZABD and ZDBC are supplementary angles.
What is the measure of x?
X = [?]°
7D
110%
AK
B.
→C
Angles are not drawn to scale.
Enter
![StatusRecoveryZABD and ZDBC are supplementary angles.What is the measure of x?X = [?]7D110%AKB.CAngles](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/ytxqB97UcRw2WjKCLIvEF9NvgAof4Yjq.png)
Answers
Answer:
jhbujnhjnv
Step-by-step explanation:
vnjhbjhbjmb
Answer:
x=70°
Step-by-step explanation:
x+110=180 linear pair
x=180-110=70
Select the correct answer from the drop-down menu. The coordinates of vertex C are ____?

Answers
Answer
The coordinates of vertex C = (5, -2)
Explanation
ABCD is supposed to be a rectangle.
And the coordinates of the remaining vertices of the triangle have been provided.
So, we know that vertex C has to be on the same vertical line (x-coordinate = 5) as vertex B and on the same horizontal line as vertex D (y-coordinate = -2)
So,
The coordinates of vertex C = (5, -2)
Hope this Helps!!!
how to write 1 in numbers ?
Answers
Answer:
To write 1 in a numerical form, you have to check its place value. It's 1. So, 1 is 1 in numerical form. :-)Selling Price = $ 504 and Gain % = 12%
Answers
Answer:
Step-by-step explanation:
sp = 504
gain = 12%
in this case
sp =100%+12%=504
112%=504
1%=504/112 =4.5
100%=450
so cost =$450
Hope im correct, if i am im glad to be of service.
A craftsperson must attach a lead strip around all four sides of a stained glass window that is
8 4/5 in. by
14 17/25 in. before it is installed. Find the length of lead stripping needed.
Answers
9514 1404 393
Answer:
46 24/25 in
Step-by-step explanation:
Opposite pairs of sides are the same length, so the total length needed is ...
2(8 4/5 +14 17/25) = 2(8 20/25 +14 17/25) = 2(22 37/25) = 2(23 12/25)
= 46 24/25 . . . inches
Stefan borrowed $8,950
for an engagement ring. At
a 6.85% simple interest rate,
how much total will he have
paid after 6 years?
Answers
The amount after 6 years is $12,628.45
Simple interestThe formula for calculating the compound interest is expressed as:
I = PRT
P is the principal = $8,950r is the rate = 6.85% = 0.0685T is the tim = 6 yearsGet the interest
I = 8950 * 0.0685 * 6
I = $3,678.45
Amount after 6 years = 8950 + 3,678.45
amount after 6 years = $12,628.45Hence the amount after 6 years is $12,628.45
Learn more on simple interest here: https://brainly.com/question/25793394
Suppose that in a large metropolitan area, 84% of all households have cable tv. Suppose you are interested in selecting a group of six households from this area. Let X be the number of households in a group of six households from this area that have cable tv. For what proportion of groups will at most three of the households have cable tv?
Answers
Answer:
0.05606
Step-by-step explanation:
This is a binomial probability distribution problem.
84% of all households have cable TV, thus;
p = 0.84
There are six households from this area, thus; n = 6
Formula for this binomial distribution is;
P(X) = C(n, x) × p^(x) × (1 - p)^(n - x)
We want to find the proportion of groups where at most three of the households have cable TV.
Thus, it's is;
P(X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
P(X = 0) = C(6, 0) × 0.84^(0) × (1 - 0.84)^(6 - 0) = 0.00001678
P(X = 1) = C(6, 1) × 0.84^(1) × (1 - 0.84)^(6 - 1) = 0.000528
P(X = 2) = C(6, 2) × 0.84^(2) × (1 - 0.84)^(6 - 2) = 0.006963
P(X = 3) = C(6, 3) × 0.84^(3) × (1 - 0.84)^(6 - 3) = 0.04855
Thus;
P(X ≤ 3) = 0.00001678 + 0.000528 + 0.006963 + 0.04855 = 0.05606
the ratio of sadia's age to her father's age is 3:6. The sum of their age is 96 .What is sadia's age?
Answers
Answer:
sadia is 32
Step-by-step explanation:
sadia : father : total
3 6 9
Divide 96 by 9
96/9 = 32/3
Multiply each by 32/3
sadia : father : total
3*32/3 6*32/3 9*32/3
32 64 96
Areceli is a chef for a catering company. The guests at a banquet had a choice of entrées: chicken or lasagna.
Areceli prepared three times as many chicken dinners as lasagna dinners, and there were 96 guests. How many chicken dinners were served?
Answers
Answer:
93x6=anser
Step-by-step explanation:
Answer:
72 Chicken Dinners and 24 Lasagna Dinners
Step-by-step explanation:
Since you know that chicken dinners are 3 times as much as lasagna, you know that you must divide 96 by 4. Why? Well we aren't just looking at the chicken dinners itself. IF we were, then we would divide 96 by 3. But in this situation, you have to divide by both the lasagna and the chicken. Adding the parts together, you get 1 and 3, or 4. So, dividing 96 by 4 you get 24. You now know that the amount of lasagna dinners is 24. Chicken dinners are 3 times as much meaning 24 x 3 = 72 chicken dinners.
Algebraic expression ish (x = lasagna dinners):
96 = 3x + x
96 = 4x (divide both sides by 4 now)
24 = x
Plssss help answer a b c d or e
