Answers
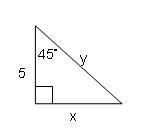
The opposite and adjacent sides are equal in length, so:
x = adjacent side = 5
Hence, the value of x is 5.
What is the right triangle?
A right-angle triangle is a triangle that has one of its angles 90 degrees. The sum of angles in a right triangle is 180 degrees.
we have given,
a right-angle triangle one angle is 45 degrees, adjacent of the angle is 5 and the opposite side is x.
In a right triangle with one angle of 45 degrees, the other acute angle is also 45 degrees.
Therefore, the opposite and adjacent sides are equal in length, so:
x = adjacent side = 5
Hence, the value of x is 5.
To learn more about the right triangle visit:
https://brainly.com/question/29869536
#SPJ1
Related Questions
Given the error function e(t) where its z-transform is: E(z) = 3z3/ z^3-9z^2+27z-27.
Prove that E(z) can be written as product of two z-transform equations E₁(z) and E₂(z) in the form E(z) = E₁ (z) x E₂ (z), where E₁(z) and E₂(z) are fractional polynomial of z of first order numerators.
Answers
The given error function E(z), with its z-transform E(z) = 3z³ / (z³ - 9z² + 27z - 27), can be expressed as the product of two z-transform equations E₁(z) and E₂(z), where E₁(z) and E₂(z) are fractional polynomials of z with first-order numerators.
To express E(z) as the product of two z-transform equations E₁(z) and E₂(z), we factorize the denominator of E(z):
E(z) = 3z³ / (z³ - 9z² + 27z - 27)
The denominator can be factored as follows:
z³ - 9z² + 27z - 27 = (z - 3)(z - 3)(z - 3)
Now, we define E₁(z) = 3z / (z - 3) and E₂(z) = z - 3. Multiplying them together, we obtain:
E₁(z) x E₂(z) = (3z / (z - 3)) x (z - 3) = 3z³ / [(z - 3)(z - 3)(z - 3)]
This expression is equal to E(z), as shown by the factored denominator. Therefore, we have proven that E(z) can be written as the product of two z-transform equations E₁(z) and E₂(z), where E₁(z) has a first-order numerator 3z and E₂(z) has a first-order numerator z - 3.
learn more about z-transform here:
https://brainly.com/question/33163485
#SPJ4
The graphs of y=f(x) and g(x) are shown below: a: -5 and 6 b: 4 and 7 c: -3,-1, and 4 d: -3,1,3 and 5

Answers
Leon earns $213 a month. If Leon saves 0.1 of his earnings, what happens to the value of each bill?
Answers
The value of each bill remains the same, as Leon is saving a percentage of his earnings without affecting the value of the bills.
Leon earns $213 a month. He saves 0.1 (or 10%) of his earnings, which is equal to $213 * 0.1 = $21.3. The value of each bill he saves remains unchanged, as he is simply setting aside a portion of his earnings without altering the value of the currency itself.
learn more about:- bill here
https://brainly.com/question/20692894
#SPJ11
Given the circle below with tangent \overline{NO} NO and secant \overline{QPO} QPO . If QP=9QP=9 and QO=14QO=14, find the length of \overline{NO} NO . Round to the nearest tenth if necessary. Q
Answers
Given that that the lengths of the parts of the secant are, QO = 14 and QP = 9, we have that the tangent, NO = 17.9
How can the length of the tangent be found?
The given parameters are;
Length of side, QP = 9
Length of QO = 14
Required;
The length of;
\( \overline{no}\)
From the tangent and secant formula, we have;
\( { \overline{no}}^{2} = { \overline{qo}} \times ( { \overline{qp} \: + { \overline{qo}}})\)
Which gives;
NO^2 = 14 × (9 + 14) = 322
NO = √(322) = 17.9
The length of the side NO = 17.9Learn more about the tangent and secant theorem here;
https://brainly.com/question/26080631
I need some help please

Answers
Answer:
segments EA and DG
Step-by-step explanation:
A diameter is when a line segment crosses the center of the circle and its endpoints lie on the circle. Both segments EA and DG satisfy the definition of a diameter.
Answer:
EA and DG
Step-by-step explanation:
For it to be a diameter, it has to pass through the center (point H) and touch both sides of the circle.
The ones that work for that are EA and DG
David uses a falling mass to split wooden logs. The 5kg mass slides down the rod and hits the metal blade. The force on the blades splits the log.
b) David lifts the mass. The mass gains 50J of gravitational potential energy. The falling mass changes this energy into kinetic energy.
i) As it falls, what is the maximum amount of energy the mass can change from gravitational potential energy to kinetic energy? ____________ J
ii) Not all the gravitational potential energy is transferred to kinetic energy as the mass falls.
Give one reason for this.
Answers
As David lifts the mass,
the maximum amount of energy the mass can change from gravitational potential energy to kinetic energy is 50 JThe exact reason why we can say that not all energy is converted to kinetic energy is because as the mass falls, there would be air resistance which would slow it down although some would still be gravitational.What is kinetic energy?This is the term that is used to refer to the energy that a body has due to the fact that the given body is on motion. The kinetic energy is the energy in motion.
What is the gravitational potential energy?This is the energy that a body would have due to the fact that it is positioned on a gravitational potential field.
Read more on kinetic energy here:
https://brainly.com/question/8101588
#SPJ1
>>RIGHT ANSWERS ONLY
A company car that has a seating capacity of six is to be used by six employees who have formed a car pool. If only four of these employees can drive, how many possible seating arrangements are there for the group?
Answers
Answer:
4
Step-by-step explanation:
3*5*4*3*2*1
3x-x+2=4
Instructions: Find the missing side. Round your answer to the nearest tenth.

Answers
Using the sine ratio, the length of the missing side is: 11.8.
How to Find Missing Side Using the Sine Ratio?The sine ratio is, sin ∅ = opposite/hypotenuse.
Given the following:
∅ = 24°
Opposite = x
Hypotenuse = 29
sin 24 = x/29
x = (sin 24)(29)
x = 11.8
Learn more about the sine ratio on:
https://brainly.com/question/2920412
#SPJ1
find the area of a rectangle that has a length of 4ab^2 and a width of 6a^2b
Answers
Answer:
Step-by-step explanation:
∵A= l×b
⇒A= 4ab^2 × 6a^2b
⇒A= 24a^2b+1×b^2
Explanation: When multiplying indices, add the exponents of similar bases (that is, a^2×a = a^2+a^1 =a³) thus a^2b+1.
I hope this helped.
need help with the picture

Answers
Answer:
E F D C A B
Step-by-step explanation:
thats the order the letters go in
Answer:
This is the order from top to bottom
E, F, D, C, A, and then B
Step-by-step explanation:
It is wanting the opposite
suppose we have a continuous random variable over -2 < x < 5. what is p(x = 1)?
Answers
We have a continuous random variable over -2 < x < 5 so p(x = 1) = 0 because the probability at any given point for any continuous random variable is always 0.
Probability is a measure of the likelihood of a particular event occurring. It is expressed as a number between 0 and 1, with 0 indicating that the event is impossible and 1 indicating that the event is certain to happen.
Probability at any given position is always zero for any continuous random variable. This is because the probability of a single value occurring for a continuous random variable is always 0 because the range of values for the random variable is infinite and therefore the probability of a single value occurring is 0.
To learn more about continuous random variable link is here
brainly.com/question/17238189
#SPJ4
Bonus: double your money! One bank promises they can double your money if you invest
with them. If that were true, and you started with just 1 penny, how many doublings would you
need to reach your pennies to the moon?
Answers
Answer:
Y'all playing with me........right???
Which equation represents a line that is perpendicular to y=2/3x−5 and passes through the point (6,12)?

Answers
The equation representing a line that is perpendicular to y=2/3x−5 and passes through the point (6,12) is y = -3x/2 +24
How to determine the equation of the line perpendicular to y=2/3x−5 and passes through the point (6,12)Equation of line perpendicular to another line is defined by the slope of the lines. If the slope is m, then the relationship between the slopes are
m = -1/m'
The equation of the line given y = 2/3x − 5
slope , m = 2/3
slope of the perpendicular line, m' = -1/m
m' = -3/2
The line passes through point (6,12)
y - 6 = -3/2(x-12
y - 6 = -3x/2 + 18
y = -3x/2 + 18 + 6
y = -3x/2 + 24
The equation of the perpendicular line required is y = -3x/2 +24
Learn more about Equation of perpendicular line here: https://brainly.com/question/7098341
#SPJ1
Blank minus 3/8 equals 3/4
Answers
Answer:
1 1/8
Step-by-step explanation:
3/4 = 6/8 ( 3x2= 6 numerator ) ( 4x2= 8 denominator )
6/8 + 3/8 = 9/8 = 1 1/8
Answer:
1 1/8
Step-by-step explanation:
3/4 = 6/8 ( 3x2= 6 numerator ) ( 4x2= 8 denominator )
6/8 + 3/8 = 9/8 = 1 1/8
find the equation of the line passing through (-4,1) and perpendicular to the line y=x/4+2
Answers
Answer:
y = -4x
Step-by-step explanation:
First, for an equation of form y=mx+b, m represents the slope. Therefore, for y=x/4+2 = (1/4)*x + 2, 1/4 is the slope. For perpendicular lines, the negative reciprocal of the slope is the slope of the line perpendicular to it. Therefore, the slope of our line is the negative reciprocal of 1/4.
To find the reciprocal of something, we can just divide 1 by it (another way to do this would be to flip the numerator and denominator, so 1/4 turns into 4/1). Therefore, 1/(1/4) = (1/1)/(1/4) = (1/1) * (4/1) = 4. The negative reciprocal is thus -4.
Our equation is therefore of form y = (-4) x + b. To solve for b, we can plug in the point given and solve for b in our equation. We have
-4 = (-4) * 1 + b
-4 = -4 + b
add 4 to both sides to isolate the b
0 = b
Therefore, our equation is
y= (-4)x + 0
y = -4x
\(.3x^2+x=.1x\) help me please this is hard
Answers
Answer:
x is equal to -3
Step-by-step explanation:
If you have a lot of problems with decimal coefficients (I know I do), you can get rid of them first. Just multiply both sides of the equation by 10:
.3x² + 1 = .1
3x² + 10x = x
Then note that each term is also divisible by x. If we factor that out, we get:
3x + 10 = 1
Which we can easily solve for x:
3x = -9
x = -3
Factorise fully :
mx + my + nx + mq
Answers
(1) 4 and 9 are factors of a number. Which of these could be the number? (A) 8 (B) 18 (C) 49 (D) 72
Answers
Answer:
(D) 72
Step-by-step explanation:
A factor is an integer that divides into a whole number without a remainder.
In this case, both 4 and 9 need to be the result of a division of 72 by some number. 4 is a factor of 8, since 8 divided by 2 is 4, but 9 isn't. 9 is a factor of 18, but 4 isn't. Neither 4 nor 9 is a factor of 49. If you divide 72 by 18, you get 4. If you divide 72 by 8, you get 9.
4 and 9 are factors of 72.
Answer:
The answer is D
72
Step-by-step explanation:
Factors of 72 are 8,9
8=2×2×2
8=4×2
1,2 3,4,6,8,9.........72
find the area of the surface. the part of the plane 13x + 5y + z = 65 that lies in the first octant
Answers
the area of the surface that corresponds to the part of the plane 13x + 5y + z = 65 lying in the first octant is 32.5 square units.
To find the area of the surface that corresponds to the part of the plane 13x + 5y + z = 65 lying in the first octant, we need to find the equation of the portion of the plane that lies in the first octant and then calculate the surface area of that portion.
First, we need to find the intercepts of the plane with the x, y, and z-axes. Setting x = 0, we get:
5y + z = 65
Setting y = 0, we get:
13x + z = 65
Setting z = 0, we get:
13x + 5y = 65
Solving these three equations simultaneously, we get:
x = 5, y = 13, z = 0
So the plane intersects the x-axis at (5,0,0), the y-axis at (0,13,0), and the z-axis at (0,0,65).
The part of the plane that lies in the first octant is bounded by the x-axis, the y-axis, and the line connecting (5,0,0) and (0,13,0). This triangular region has a base of length 5 and a height of 13, so its area is (1/2)513 = 32.5.
To know more about area visit:
brainly.com/question/1631786
#SPJ11
2000x100 guesss yall
Answers
Answer:
200,000
Step-by-step explanation:
help
me
do
this
im
about
to
fail

Answers
Answer:
4.89 the rounding of it is 5.00,
Area=(22 over 7) x5^2
=78.57cm^2
Hope that helps
Consider a population of 1,024 mutual funds that primarily invest in large companies. Hannah has determined that μ, the mean one-year total percentage return achieved by all the funds, is 7.10 and that σ, the standard deviation, is 3.50.
According to the Chebyshev rule, what percentage of these funds are expected to be within ±6 standard deviations of the mean? _____ (Round to 2 decimal places as needed.)
Answers
The percentage of these funds are expected to be within ±6 standard deviations of the mean is 97.22% (approx).Hence, the required answer is 97.22.
The Chebyshev’s theorem is used to determine the percentage of observations that lie within a certain number of standard deviations of the mean in a set of data.
According to the Chebyshev rule, what percentage of these funds are expected to be within ±6 standard deviations of the mean can be calculated using the formula:
\($$1 - \frac{1}{k^2}$$\)
Where k is the number of standard deviations. For the question, the mean is 7.10 and standard deviation is 3.50.As per the given data, we can find that, the number of standard deviation from the mean is ±6.
Thus, k = 6.
The percentage of these funds are expected to be within ±6 standard deviations of the mean is:
\($$1 - \frac{1}{k^2} = 1 - \frac{1}{6^2} = 1 - \frac{1}{36} = 0.9722$$\)
Therefore, the percentage of these funds are expected to be within ±6 standard deviations of the mean is 97.22% (approx).
Hence, the required answer is 97.22.
For more such questions on percentage , Visit:
https://brainly.com/question/30744872
#SPJ8
people taking part in an experiment are called variables.
Answers
Answer:
Yes, people that taking part in an experiment are called variables.
There is normally one person called the dependent variable, and the other who is the independent variable.
The statement provided "people taking part in an experiment are called variables" is incorrect.
In an experiment, the individuals or subjects who participate and are observed or manipulated are not referred to as variables. Instead, they are called participants, subjects, or sometimes, respondents, depending on the context of the study.
Variables, on the other hand, are characteristics or properties that can vary or change among the individuals or subjects in the study. Variables can be classified as independent variables, dependent variables, or control variables.
Independent variables are manipulated or controlled by the researcher, while dependent variables are the outcomes or responses that are measured or observed.
Control variables are other factors that are held constant. Therefore, it is important to differentiate between the individuals participating in the experiment and the variables being studied.
To know more about variables refer here:
https://brainly.com/question/15078630
#SPJ11
Two linear functions are shown below. Which function has the greater rate of change? Use the drop-down menus to show your answer. Function A Function B x y 0 1 4 2 8 3 12 4 y = 34 3 4 x –2
Answers
The required, rate of change of function B is greater than the rate of change of Function A.
What is the rate of change?Rate of change is defined as the change in value with rest to another entity is called rate of change.
Here,
For function 1 rate of change is given by the slope of the function,
m = (y₂ - y₁) / (x₂ - x₁)
m = 2 - 1 / 4 - 0
m = 1/4
m = 0.25
For function B, y = 0.75x - 2 rate of change has defined the slope of the function from the equation slope is m = 0.75.
So Slope of function B > Slope of function A
Thus, the rate of change of function B is greater than the rate of change of Function A.
Learn more about the rate of change here: https://brainly.com/question/13103052
#SPJ1

Someone please help!! I have to finish this and Im dum.b lol
(( Ignore the first answer, I didnt mean to put true-)

Answers
Answer:
1) False
2) True
3) True
4) False
Step-by-step explanation:
For the first statement, we can look at a graph with the line of y = 3.69x plotted. If we check the points (7.38, 2) and (11.07,3), they do not intersect with the line. So, the first statement is false.
For the second statement, we can check the equation for the line to find the slope. The equation, y = 3.69x, is in slope-intercept form, or \(y = mx + b\). In this form, \(m\) is the slope of the line. \(b\) is the y-intercept. In this line, there is no y-intercept specified, so we can take this to mean the y-intercept is 0. The slope, we can see, is 3.69. The slope, multiplied by x, shows us any point of the line. The second statement, then, is true.
The next statement can be verified by finding just how much 16 gallons will cost. Like we've seen before, the slope can be multiplied by x, the number of gallons, to see where that point will be plotted. So, we can multiply the slope by 16.
3.69 · 16 = 59.04
The (x) value, we already know, is 16. The (y) value, we've found, is 59.04. So 16 gallons will be plotted at (16, 59.04). The third statement is true.
The last statement says that if the price increases by $0.05, the slope will be 3.64. We can tell this is false by adding 0.05 to the original slope, 3.69.
3.69 + 0.05 = 3.74
3.74 ≠ 3.64, so the last statement is false.
I hope this was helpful to you ^^
Good luck
Write an equation that is parallel to 3x- 2y = 14 and passes through the point (-6, -11).
Answers
Answer:
y=3/2x-2
Step-by-step explanation:
Since it is parallel it will have the same slope. Put the equation into y=mx+b form in order to easily identify the slope. 3x-2y=14. Subtract the 3x and divide by -2......From there you can see that the equation is y=-7 +3/2x. We cannot keep the -7 since it is parallel and wont have the same y intercept. Plug in the -11 for the y and the -6 for the x and solve for b (the new y int.) It should look like -11= 3/2(-6) +b....From there b should be -2. Final step is to rewrite the equation to be y=3/2x-2!
validity of short forms may be reduced because fewer items
Answers
The validity of short forms may be reduced because they contain fewer items compared to the full-length version. Short forms of tests or questionnaires are often used in research and clinical settings due to their convenience and efficiency.
This means that the short form may not fully capture the construct being measured and may not accurately reflect the individual's true scores. Additionally, the items selected for the short form may not be representative of the full range of the construct, leading to bias and limited generalizability.
Therefore, researchers and clinicians should consider the trade-offs between convenience and validity when deciding to use short forms.
To know more about short forms:
https://brainly.com/question/3108505
#SPJ4
Let each of the following be a relation on {1,2,3}. which one is symmetric? a. {(a,b)|a=b}. b. {(a,b)|a>=b}. c. {(a,b)|a>b}. d. {(a,b)|a
Answers
Based on the given options, the relation that is symmetric is option A: {(a,b)|a=b}.
A relation is symmetric if for every (a, b) in the relation, (b, a) is also in the relation. In this case, for the relation to be symmetric, every element (a, b) in the relation must have its corresponding element (b, a) in the relation.
In option A, {(a,b)|a=b}, every element (a, b) in the relation is such that a is equal to b. For example, (1, 1), (2, 2), and (3, 3) are all part of the relation. Since the relation includes the corresponding elements (b, a) as well, it is symmetric.
To summarize, option A: {(a,b)|a=b} is the symmetric relation among the given options.
Know more about relation here,
https://brainly.com/question/31111483
#SPJ11
Mr. Forest drew a diagram of his office on a coordinate grid. He placed his chair at (4, 3), his podium at (4, -4), and his desk at (-6, -4). The length of each square on the grid represented one yard. What was the distance between the podium and the desk?
Answers
The distance between the podium and the desk is given as follows:
10 yards.
How to calculate the distance between two points?Suppose that we have two points of the coordinate plane, and the ordered pairs have coordinates given by \((x_1,y_1)\) and \((x_2,y_2)\).
The distance between them is given by the equation presented below as follows, derived from the Pythagorean Theorem:
\(D = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
The coordinates for this problem are given as follows:
Podium: (4, -4).Desk: (-6, -4).Hence the distance is obtained as follows:
\(D = \sqrt{(4 - (-6))^2 + (-4 - (-4))^2}\)
D = 10 yards. (as each unit is 10 yards).
More can be learned about the distance between two points at https://brainly.com/question/7243416
#SPJ1
in the expression 3x+7 what is the coefficient
Answers
Answer:
3
Step-by-step explanation:
Coefficient in the number behind the variable.
In 3x + 7,
x is the variable.
3 is the coefficient.