Find the whole number equal to the fraction below. Enter your answer in the
space provided

Answer:

4x - 4

Step-by-step explanation:

Add up all common numbers and then subtract from the total amount.

Hope it helps :))

Using the formula of volume of a sphere and hemisphere, the volume of the figures are given as;

1. 2144.57 m³

2. 696.6 m³

3. 20569.1m³

4. 2637ft³

5. 56.5km³

6. 6381.79 in³

The volume of a sphere is given as 4/3πr³

Where π is a constant whose value is equal to 3.14 approximately. “r” is the radius of the hemisphere.

1. The volume of the sphere is;

v = 4/3 * 3.14 * 8³ = 2144.57m³

2. The volume of the sphere is;

v = 4/3 * 3.14 * (11/2)³ = 696.6m³

3. The volume of the sphere is;

v = 4/3 * 3.14 * 17³ = 20569.1m³

4. The volume of the hemisphere is;

v = 2/3 * 3.14 * 10.8³ = 2637ft³

5. The volume of the hemisphere is;

v = 2/3 * 3.14 * 3³ = 56.5km³

6. The volume of the hemisphere is;

v = 2/3 * 3.14 * (29/2)³ = 6381.79in³

Learn more on volume of sphere here;

https://brainly.com/question/22807400

#SPJ1

1) The probability distribution of the average weekly earnings for employees in general automotive repair shops is the sampling distribution of the sample mean. According to the Central Limit Theorem, if the sample size is large enough, the sampling distribution of the sample mean is approximately normal, with a mean equal to the population mean and a standard deviation equal to the population standard deviation divided by the square root of the sample size.

2) To find the probability that the average weekly earnings is less than $445, we can standardize the sample mean and use a z-table. The z-score for $445 is calculated as follows: z = (445 - 450) / (50 / sqrt(100)) = -1. Using a z-table, we find that the probability that the average weekly earnings is less than $445 is approximately 0.1587.

3) Since we are dealing with a continuous distribution, the probability that the average weekly earnings is exactly equal to any specific value is zero.

4) To find the probability that the average weekly earnings is between $445 and $455, we can subtract the probability that it is less than $445 from the probability that it is less than $455. The z-score for $455 is calculated as follows: z = (455 - 450) / (50 / sqrt(100)) = 1. Using a z-table, we find that the probability that the average weekly earnings is less than $455 is approximately 0.8413. Therefore, the probability that it is between $445 and $455 is approximately 0.8413 - 0.1587 = 0.6826.

5) In answering questions 2-4, we made an assumption about the population distribution based on the Central Limit Theorem. We assumed that since our sample size was large enough (n=100), our sampling distribution would be approximately normal.

6) If we assume that weekly earnings for employees in all general automotive repair shops are normally distributed with a mean of $450 and a standard deviation of $50, then we can calculate the z-score for an employee earning more than $480 in a given week as follows: z = (480 - 450) / 50 = 0.6. Using a z-table, we find that the probability that an employee will earn more than $480 in a given week is approximately 1 - 0.7257 = 0.2743.

To ensure that there is an equal number of glass bears in each group, Mrs. Dryson constructed a total of 17 groups, which can be calculated using arithmetic operations.

What is arithmetic operations?

The study and application of numbers in all other fields of mathematics are covered in the area of mathematics known as arithmetic operations. Addition, subtraction, multiplication, and division are included in the basic operations.

As given in the question,

Mrs. Dryson divided her collection of 52 glass bears into equal groups and She had one bear left over

The steps listed below can be used to calculate the total amount of Mrs. Dryson's products:

Step 1: Arithmetic operations can be utilized to calculate Mrs. Dryson's overall output.

Step 2: Keep in mind that there are 52 glass bears in all, and after separating them into equal groups, she was left with just one bear.

Step 3 - The total bear population to divide into groups of an equal number is calculated as follows:

= 52 - 1 = 51

Step 4: The number that is divided by 51 such that the result is an integer is 3.

Step 5 - As a result, Mrs. Dryson created a total of the following groups:

= 51/3 = 17.

To know more about arithmetic operations, go to link

https://brainly.com/question/4721701

#SPJ1

Answer:

6. (27÷3) × v = 45

9 × v = 45

v = 45/9 = 5

F. 5

5. (2×19) + 3 = j

38 + 3 = j

j = 41

C. 41

4. 7 + t = 4 + 6 + 3

t = 13 - 7

t = 6

J. 7+t = 4+6+3

t = 6 tickets

Answer:

First question=5 : Second question= 41 : Third question= J

Step-by-step explanation:

27 divided by 3 is 9, so planting one violet takes 9 minutes, if they spend 45 minutes planting them you divide 45 by 9 and get 5.

:)

Ada ate 19, rob ate double Adas amount, so 19x2 to get Robs total of 38, then Jane ate 3 more than rob, so 38+3=41

:)

6 is the 13 tickets she needs -7 that she has already.

your answer would be 254 I just did it and I got it right ✨

Andy would pay $23.94 more in finance charges compared to Brett, given their respective APRs, average daily balances, and monthly percentage rates.

To calculate the monthly percentage rate (MPR) from the given annual percentage rate (APR), we divide the APR by 12.

For Brett:

APR = 12.6%

MPR = 12.6% / 12 = 1.05%

For Andy:

APR = 16.2%

MPR = 16.2% / 12 = 1.35%

Next, we can calculate the finance charge for each individual using the formula: finance charge = average daily balance * MPR.

For Brett:

Finance charge = $7,980 * 1.05% = $83.79

For Andy:

Finance charge = $7,980 * 1.35% = $107.73

To find the difference in the finance charges between Andy and Brett, we subtract Brett's finance charge from Andy's finance charge:

Difference = $107.73 - $83.79 = $23.94

For more such on questions on percentage

https://brainly.com/question/30744872

#SPJ8

Answer:

At a package weight of 8 kilograms, the two couriers both cost $37

Step-by-step explanation:

Let's say the package weighs w kg.

First courier: 13 + 3 per kg = 13 + 3 for each w = 13 + 3w

Second courier: 5 + 4w

They are equal in cost, so

13 + 3w = 5 + 4w

subtract 3w from both sides to put all the variables on one isde

13 = 5 + w

subtract 8 from both sides to solve for w

w = 8

plug w=8 into one side of the original equation to solve for cost

13 + 3w = 5 + 4w = 37

B is true, so we can conclude ~~A by disjunctive syllogism.

This proof is based on the inference rules you provided.

D Proof: Premises:

C ---> (~D ---> ~X)

The Modus Ponens Rule was used.

Finally, X /D

Explanation: Using Modus Ponens, we can conclude that D ---> X from premises 1 and 2.

Because premise 2 is true, we can conclude X via modus tollens.

We can conclude that D must be false because X is true.

Evidence for C:

Conditions: A ---> B B

Modus Tollens is the rule that was used.

Finally, C / A

Explanation: Using Modus Tollens, we can conclude from premises 1 and 2 that A.

Because A is false in premise 1, we can conclude that B is true.

Because premise 2 is true, we can conclude C using disjunctive syllogism.

Proof for ~~A:

Premises:

A ---> ~D

~D ---> (~B v ~~A)

A

B

Rule used: Modus Ponens

Conclusion:

~~A /B

Explanation:

From premise 1 and 3, using Modus Ponens, we can conclude that ~D.

From premise 2 and ~D, using Modus Ponens, we can conclude that ~B v ~~A.

From premise 4, B is true, so we can conclude ~~A by disjunctive syllogism.

To learn more about syllogism.

https://brainly.com/question/21635821

#SPJ4

Answer:3x+y=-8

Step-by-step explanation: If you were to solve each equation by graph the slope would be negative 3

The total area from the graph is 2.737.

Area is the amount of space occupied by a two-dimensional figure. In other words, it is the quantity that measures the number of unit squares that cover the surface of a closed figure. The standard unit of area is square units which is generally represented as square inches, square feet, etc.

First of all, lets calculate the points of intersection (P, Q, R)

x²+3=(x+2) +5

x²-2=√(x+2)

x⁴+4-4x²=x+2

x⁴-4x²-x+2=0

(x-2)(x³+2x²-1)=0

(x-2)(x+1)(x²+x-1)=0

x=2, -1, -1±√(1+4)/2

Clearly, the x-coordinate of Q is -1, P is -1-√5/2, R is -1+√5/2, S is 2

So the limit of integration will be

P( (-1-√5)/2, (-1-√5/2)² +3)=P((-1-√5)/2, (3+√5/2))

Q(-1, (-1)²+3)=Q(-1, 4)

Area A:

\(\int\limits^\frac{3+\sqrt{5} }{2} _4 {-\sqrt{-y-3}-((y-5)^2 -2)} \, dx\)

= \([\frac{-(y-3)^\frac{3}{2} }{\frac{3}{2} }-\frac{(y-5)^3}{3}+3y]^{\frac{3+\sqrt{5} }{2} }_4\)

= 2.07

Area B:

\(\int\limits^\frac{-1+\sqrt{5} }{2} _4 {-\sqrt{x+2}+5-(x^2+3)} \, dx\)

= \([\frac{-(x+2)^\frac{3}{2} }{\frac{3}{2} }+5x-\frac{x^3}{3}-3x]^{\frac{-1+\sqrt{5} }{2} }_{-1}\)

= 0.667

Total area = 2.07+0.667

= 2.737

Therefore, the total area from the graph is 2.737.

Learn more about the area here:

https://brainly.com/question/27683633.

#SPJ1

Answer:

Step-by-step explanation:

8x² - 30x - 27 = 0

8 = 4 * 2

-27 = -9 * 3

-30 = 4*(-9) + 2*3

so (4x + 3)(2x - 9) = 0

Answer:

x=1. 3*1=3 so we'll say 3 instead of 3x. ([6*2]+[3*2])=(6*3)

P.s.

Can you please give me brainliest for my next rank.

The binomial factors of x³- 4x²+x+6​ are (x+2), (x+3), and (x-1).

Using the splitting and grouping the terms:

x³ + 4x² + x - 6

= x³ + 2x² + 2x² + x - 6  [Splitting 4x² = 2x² + 2x²]

= (x³ + 2x²) + (2x² + x - 6)

= x² (x + 2) + (2x² + 4x - 3x - 6)

= x² (x + 2) + [ 2x (x + 2) - 3 (x + 2)]

= x² (x + 2) + (x + 2) (2x - 3)

= (x + 2) ( x² + 2x - 3)

= (x + 2) ( x² + 3x - x - 3)

= (x + 2) [x (x + 3) - 1 (x + 3)]

= (x + 2) (x + 3) (x - 1)

Hence, the binomial factors are (x + 2), (x + 3) and (x - 1)

To learn more about factorise here,

https://brainly.com/question/10718512

https://brainly.com/question/24734894

Answer:

2,4,6,

6,12,18

10,20,30

a) To express FB in terms of b, we need to consider the relationship between FB and EF. Since EF is equal to 2a, we can substitute this value into the expression for FB:

FB = EF - FB

= (2a) - (2a)

= 0

Therefore, FB is equal to 0 in terms of b.

b) To express FD in terms of a and b, we can use the given relationship between ED and FD. ED is equal to 3b, so we can substitute this value into the expression for FD:

FD = ED - FB

= (3b) - (0)

= 3b

Therefore, FD is equal to 3b in terms of a and b.

c) To express CB in terms of a and b, we need to consider the relationship between CB and EF. Since EF is equal to 2a, we can substitute this value into the expression for CB:

CB = EF - EB

= (2a) - (FB + FD)

= (2a) - (0 + 3b)

= 2a - 3b

Therefore, CB is equal to 2a - 3b in terms of a and b.

Answer:

x = 2

Step-by-step explanation:

Angles ABN and NBC are adjacent angles and sum up to angle ABC

Answer: $0.576

Step-by-step explanation:

The total amount in prizes is $1800.

For there to be 60% profit, the total cost of the tickets need to be \(1800(1.6)=\$ 2880\).

Thus, each ticket must sell for \(\frac{2880}{5000}=\$ 0.576\)

The algorithm/abstract strategy to justify the fraction 3/5 involves interpreting it as a division, performing the division, and obtaining the decimal representation as the results.

To justify the fraction 3/5, we can use the concept of division and understand it as a ratio or proportion.

Algorithm/Abstract Strategy:

Start with the numerator, which is 3.

Identify the denominator, which is 5.

Interpret the fraction as a ratio or comparison between the numerator and denominator.

Understand that 3/5 represents a division where the numerator (3) is divided by the denominator (5).

Perform the division: 3 ÷ 5.

Simplify the division to its simplest form, if necessary.

The result of the division, in this case, is the decimal representation of the fraction.

If required, convert the decimal representation to a percentage or any other desired form.

For example, if we perform the division 3 ÷ 5, the result is 0.6.

So, 3/5 can be justified as the ratio or proportion where the numerator (3) is divided by the denominator (5) resulting in 0.6.

For similar question on algorithm/abstract strategy.

https://brainly.com/question/31332020  

#SPJ8

The velocities of the boat and the person relative to the shore are 1.337 m/s and 2.896 m/s, respectively.

We can use the conservation of momentum equation:

(mboat + mperson) * vboat = mperson * vperson

(160 kg + 70 kg) * vboat = 70 kg * (0.80 m/s + vperson)

230 kg * vboat = 56 kg * (0.80 m/s + vperson)

vboat = (56/230) * (0.80 m/s + vperson)

vperson = 0.80 m/s + vboat

vperson = 0.80 m/s + (56/230) * (0.80 m/s + vperson)

(174/115) * vperson = (504/115) * m/s

Dividing both sides by (174/115), we get:

vperson = 2.896 m/s

vboat = (56/230) * (0.80 m/s + vperson)

Substituting the value of vperson, we get:

vboat = 1.337 m/s

Learn more about velocity on

https://brainly.com/question/25749514

#SPJ1

On a 160-kg boat that is at rest with its bow pointed to the shore, a 70-kg person begins to walk from the bow to the stern at 0.80 m/s relative to the boat. What are the velocities of the boat and the person relative to the shore? Neglect the resistance of water to motion.

Answer:

386.75

Step-by-step explanation:

added in the picture

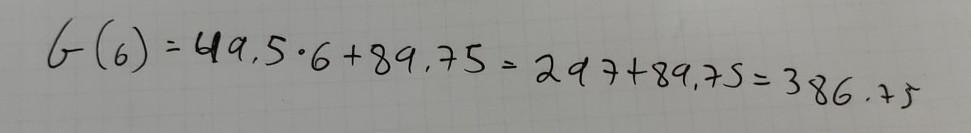
The cost of joining the gym for 6 months is 386.75.

Given,

The function G(m) = 49.5m + 89.75 represents the cost of joining the gym in addition to the one-time membership fee.

The cost, G, is measured in dollars for m months.

We need to find the value of G(6).​

Here,

The one-time membership = 89.75.

Now,

Putting m = 6 months in:

G(m) = 49.5m + 89.75

G(6) = 49.5 x 6 + 89.75

       = 297 + 89.75

       = 386.75

Thus the cost of joining the gym for 6 months is G(6) = 386.75.

Learn more about finding the value of a function here:

https://brainly.com/question/8822000

#SPJ2

Answer:

360 degrees

2 pi radians, means you have 2 pi of something and they are radians. It is the same 360 degrees. A radius is the line from the side of the circle to the center.

Reason: pi radians is 180 degrees. Double each value to find that 2pi radians is 360 degrees. It's a full revolution of a circle. Use a unit circle if necessary.

Answer:

answer is 3.2

Step-by-step explanation:

Simplifying

8[4 + -1a] = 2a

[4 * 8 + -1a * 8] = 2a

[32 + -8a] = 2a

Solving

32 + -8a = 2a

Solving for variable 'a'.

Move all terms containing a to the left, all other terms to the right.

Add '-2a' to each side of the equation.

32 + -8a + -2a = 2a + -2a

Combine like terms: -8a + -2a = -10a

32 + -10a = 2a + -2a

Combine like terms: 2a + -2a = 0

32 + -10a = 0

Add '-32' to each side of the equation.

32 + -32 + -10a = 0 + -32

Combine like terms: 32 + -32 = 0

0 + -10a = 0 + -32

-10a = 0 + -32

Combine like terms: 0 + -32 = -32

-10a = -32

Divide each side by '-10'.

a = 3.2

Simplifying

a = 3.2

Answer:

a = 3.2

Step-by-step explanation:

if the linear equation is: 8 (4-a)=2a the value of a would be 3.2 because

a = 16/5 which equals to 3 1/5 which is the same as 3.2

Answer:

B

Step-by-step explanation:

It's b my correct answer is b

Answer:

y=-7

Step-by-step explanation:

y=3(-4)+5

y=-12+5

y=-7

Answer:

242.50 \(cm^{2}\)

Step-by-step explanation:

V = \(\pi r^{2}\)h

4850 = \(\pi r^{2}\) (20)  Divide both sides by 20

242.5 = \(\pi r^{2}\) The area of the base is \(\pi r^{2}\)

Helping in the name of Jesus.