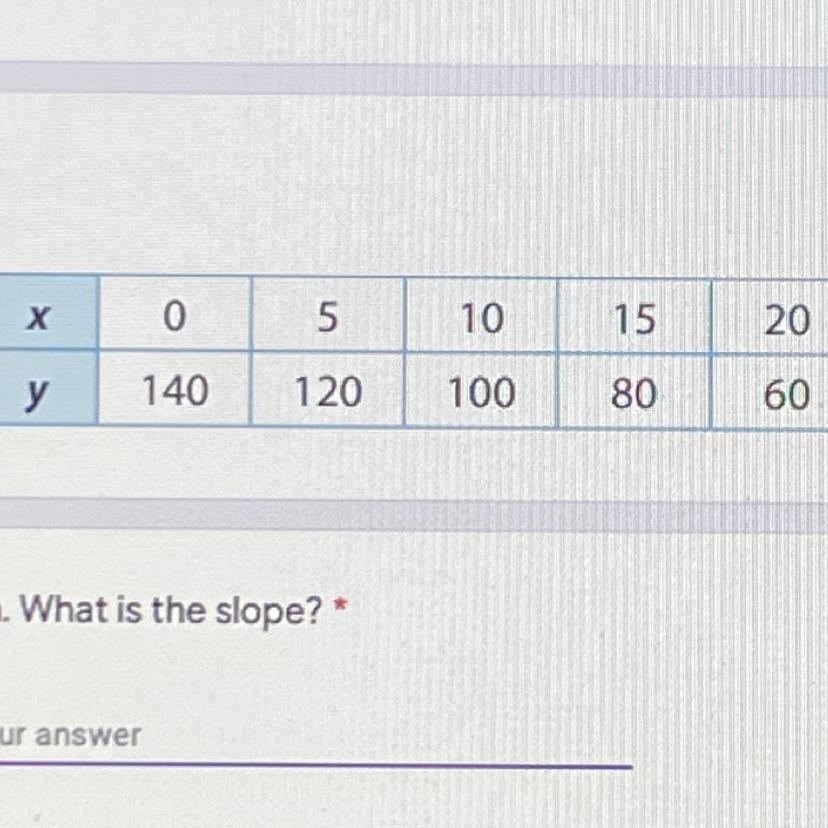
Answers
y-int: 140
slope: -4
to find the slope u gotta use the (y2-y1)/(x2-x1) formula
120-140 = -20
5-0 = 5
-20/5 = -4
Related Questions
please help me
A scientist is studying the growth of a particular species of plant. He writes the following equation to show the height of the plant f(n), in cm, after n days:
f(n) = 12(1.03)n
Part A: When the scientist concluded his study, the height of the plant was approximately 16.13 cm. What is a reasonable domain to plot the growth function? (4 points)
Part B: What does the y-intercept of the graph of the function f(n) represent? (2 points)
Part C: What is the average rate of change of the function f(n) from n = 3 to n = 10, and what does it represent? (4 points)
(10 points)
Answers
The required answers are Part A: Domain: {n | n is a positive integer}, Part B: 12, Part C: 0.98 cm/day.
How to deal exponential function?Part A:
To plot the growth function f(n), we need to consider a reasonable domain that includes all relevant values of n. Since we are dealing with the growth of a plant, the domain should only include positive integers, as it does not make sense to talk about fractional or negative days. Therefore, a reasonable domain to plot the growth function would be:
Domain: {n | n is a positive integer}
Part B:
The y-intercept of the graph of the function f(n) is the value of f(0), which can be found by substituting n = 0 into the equation:
\($f(0) = 12(1.03)^0 = 12(1) = 12\)
Therefore, the y-intercept of the graph represents the initial height of the plant, which is 12 cm.
Part C:
The average rate of change of the function f(n) from n = 3 to n = 10 can be found using the formula:
Average rate of change = (f(10) - f(3))/(10 - 3)
We can evaluate f(10) and f(3) using the given equation:
f(10) = 12(1.03)^10 ≈ 18.27
f(3) = 12(1.03)^3 ≈ 13.41
Substituting these values into the formula, we get:
\($Average rate change=\frac{(f(10) - f(3))}{10-3} \approx0.98\)
Therefore, the average rate of change of the function f(n) from n = 3 to n = 10 is approximately 0.98 cm/day. This represents the average daily growth rate of the plant during this period.
To know more about Exponential function visit:
brainly.com/question/14355665
#SPJ1
What is the quotient (3x2 4x − 15) ÷ (x 3)? 3x 5 3x − 5 3x 1 3x − 1, r = 1
Answers
By solving the expression (3x2 +4x − 15) ÷ (x +3) the quotient is 3x-5 and r=0
What do you meant by quotient?When solving a division problem, the quotient is obtained by dividing the dividend by the divisor.
Mathematically, we denote the outcome of this division by separating the quotient and remainder with a capital R. (see below). The entire number that results from simplifying a fraction is known as the quotient.
We can do it by long division method the required quotient is 3x-5 and r=0
not 3x-1 , r=1
multiply the divisor with 3x we will get 3x²+9x to cancel out the first term of dividend.
Now after solving we will get -5x -15
Now, multiply the divisor by -5 we will get -5x-15 which will cancel the entire dividend.
So that the quotient is 3x-5 and r=0
To learn more about quotient visit:
brainly.com/question/11418015
#SPJ4
Let f(x) be a quadratic polynomial such that f(-4) = -22, f(-1)=2, and f(2)=-1. Let g(x)=f(x)^16. Find the sum of the coefficients of the terms in g(x) with even exponents. For example, the sum of the coefficients of the terms in -7x^3 + 4x^2 + 10x - 5 with even exponents is (4) + (-5) = -1.
Answers
Answer:
-2
Step-by-step explanation:
The probability that the interval estimation procedure will generate an interval that contains the actual value of the population parameter being estimated is the _____.
Answers
The population parameter being estimated is the confidence coefficient.
What is a confidence coefficient?The confidence coefficient is the confidence level stated as a proportion, rather than as a percentage. For example, if you had a confidence level of 99%, the confidence coefficient would be . 99. In general, the higher the coefficient, the more certain you are that your results are accurate.
probability is the likelihood that something will occur. When we don't know how an event will turn out, we can discuss the likelihood or likelihood of several outcomes. Statistics is the study of events that follow a probability distribution.
The area of mathematics known as probability deals with numerical representations of the likelihood that an event will occur or that a statement is true. An event's probability is a number between 0 and 1, where, roughly speaking, 0 denotes the event's impossibility and 1 denotes certainty.
Hence, The probability that the interval estimation procedure will generate an interval that does not contain the actual value of the population parameter being estimated is the confidence coefficient.
To learn more about the confidence coefficient from the given link:
https://brainly.com/question/28315730
#SPJ4
Matti is making moonshine in the woods behind his house. He’s
selling the moonshine in two different sized bottles: 0.5 litres
and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for
a
Answers
Based on the calculation, it appears that Matti had approximately 94 bottles of 0.5 litres and 11 bottles of 0.7 litres in the last patch of moonshine that he sold.
To solve the problem using the determinant method (Cramer's rule), we need to set up a system of equations based on the given information and then solve for the unknowns, which represent the number of 0.5 litre bottles and 0.7 litre bottles.
Let's denote the number of 0.5 litre bottles as x and the number of 0.7 litre bottles as y.
From the given information, we can set up the following equations:
Equation 1: 0.5x + 0.7y = 16.5 (total volume of moonshine)
Equation 2: 8x + 10y = 246 (total earnings from selling moonshine)
We now have a system of linear equations. To solve it using Cramer's rule, we'll find the determinants of various matrices.
Let's calculate the determinants:
D = determinant of the coefficient matrix
Dx = determinant of the matrix obtained by replacing the x column with the constants
Dy = determinant of the matrix obtained by replacing the y column with the constants
Using Cramer's rule, we can find the values of x and y:
x = Dx / D
y = Dy / D
Now, let's calculate the determinants:
D = (0.5)(10) - (0.7)(8) = -1.6
Dx = (16.5)(10) - (0.7)(246) = 150
Dy = (0.5)(246) - (16.5)(8) = -18
Finally, we can calculate the values of x and y:
x = Dx / D = 150 / (-1.6) = -93.75
y = Dy / D = -18 / (-1.6) = 11.25
However, it doesn't make sense to have negative quantities of bottles. So, we can round the values of x and y to the nearest whole number:
x ≈ -94 (rounded to -94)
y ≈ 11 (rounded to 11)
Therefore, based on the calculation, it appears that Matti had approximately 94 bottles of 0.5 litres and 11 bottles of 0.7 litres in the last patch of moonshine that he sold.
for such more question on litres
https://brainly.com/question/27877215
#SPJ8
Question
Matti is making moonshine in the woods behind his house. He’s selling the moonshine in two different sized bottles: 0.5 litres and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for a 0.7 litre bottle 10€. The last patch of moonshine was 16.5 litres, all of which Matti sold. By doing that, he earned 246 euros. How many 0.5 litre bottles and how many 0.7 litre bottles were there? Solve the problem by using the determinant method (a.k.a. Cramer’s rule).
Fiona has a coupon for $3 off the price of her meal at a local fast food establishment. her favorite meal is on sale at a special rate of 10% off the combo price. if fiona paid $8.25 for her meal, before taxes, what was the original price of the meal?
Answers
The Original price of the meal was $12.16.
Discount Percent is defined as the discount given on the product per hundred .
For Example . if there is 10% discount on a price of $100.
The final amount will be $90.
Final amount paid by Fiona = $8.25
percentage discount = 10%
Let the original amount be x.
According to the question ;
x - 10% of x = 8.25
\(x-\frac{10}{100} *x=8.25\\ \\ \frac{100x-10x}{100} =8.25\\ \\ \frac{90x}{100} =8.25\\ \\ x=\frac{8.25*100}{90}\\ \\ x=\frac{825}{90} \\ \\ x=9.16\)
Since Fiona also had a discount coupon of $3.
The original amount will be $9.16+$3=$12.16.
Therefore , The original price of the meal was $12.16.
Learn more about Discount Percent here https://brainly.com/question/14587503
#SPJ4
A and B are corresponding angles the measure of A is 110 Find B
Answers
Answer:
i think 70
Step-by-step explanation:
brainliest plz
Marian Plunket owns her own business and is considering an investment. if she undertakes the investment, it will pay $28,000 at the end of each of the new 3 years. the opportunity requires an initial investment of $7,000 plus an additional investment at the end of the second year of $35,000. what is the NPV of this opportunity if the interest rate is 8% per year? Should Marian take it?
Answers
The NPV is positive, it is worth taking the Investment.
Net Present Value (NPV) is an assessment method that determines the attractiveness of an investment. It is a technique that determines whether an investment has a positive or negative present value.
This method involves determining the future cash inflows and outflows and adjusting them to their present value. This helps determine the profitability of the investment, taking into account the time value of money and inflation.The formula for calculating NPV is:
NPV = Σ [CFt / (1 + r)t] – CIWhere CFt = the expected cash flow in period t, r = the discount rate, and CI = the initial investment.
The given problem can be solved by using the following steps:
Calculate the present value (PV) of the expected cash inflows:
Year 1: $28,000 / (1 + 0.08)¹ = $25,925.93Year 2: $28,000 / (1 + 0.08)² = $24,009.11Year 3: $28,000 / (1 + 0.08)³ = $22,173.78Total PV = $72,108.82
Calculate the PV of the initial investment: CI = $7,000 / (1 + 0.08)¹ + $35,000 / (1 + 0.08)²CI = $37,287.43Calculate the NPV by subtracting the initial investment from the total PV: NPV = $72,108.82 – $37,287.43 = $34,821.39
Since the NPV is positive, it is worth taking the investment.
For more questions on Investment.
https://brainly.com/question/29227456
#SPJ8
Identify the property that justifies each step asked about in the answer area below.
\text{Line 1: }\phantom{=}
Line 1: =
\,\,(4x)(7y)
(4x)(7y)
\text{Line 2: }\phantom{=}
Line 2: =
\,\,4\cdot (x\cdot 7)\cdot y
4⋅(x⋅7)⋅y
\text{Line 3: }\phantom{=}
Line 3: =
\,\,4\cdot (7\cdot x)\cdot y
4⋅(7⋅x)⋅y
\text{Line 4: }\phantom{=}
Line 4: =
\,\,(4\cdot 7)(x\cdot y)
(4⋅7)(x⋅y)
\text{Line 5: }\phantom{=}
Line 5: =
\,\,28xy
28xy
Line 1 to Line 2:
Line 2 to Line 3:
Line 3 to Line 4:
Answers
The multiplication properties that justify each step are given as follows:
Line 1 to Line 2: Associative property.Line 2 to Line 3: Commutative property.Line 3 to Line 4: Associative property.What are the multiplication properties?The multiplication properties used in this problem are the associative property and the commutative property, defined as follows:
Associative property: When more than two terms are multiplied, the order in which they are multiplied does not change the product.Distributive property: When more than two terms multiplied, the order in which they are multiplied does not change the product.Hence the associative property was used from line 1 to line 2 and from line 3 to line 4, as the parenthesis defines which operation was made first.
Then the distributive property was used from line 2 to line 3, as the order of the terms x and 10 was exchanged.
Missing InformationThe problem is given by the image shown at the end of the answer.
More can be learned about multiplication properties at https://brainly.com/question/13181
#SPJ1
In each figure below, find m∠1 and m∠2 if a||b. Show your work with statements.
Answers
Answer:
m < 1 = 80
m < 2 = 70
Step-by-step explanation:
As we can see in the figure that
\(a || b\)
Plus line s and t are considered to be transversals
That results into
m < 1 and 80
i.e alternate angles
And as we know that alternative angles are equal to each other
So,
m < 1 = 80
Moreover,
m < 2 = 70
As corresponding angles are equal to each other
Therefore the m < 1 = 80 m < 2 = 70 could be computed easily by applying the above things
If u are selling 5 cans of soup for $12.75 how much is each of them
Answers
Answer:
63.75
Step-by-step explanation:
12.75 times 5
A helicopter with mass 2.7×10
4
kg has a position given by
r
(t)=(0.020t
3
)
i
^
+(2.2t)
j
^
−(0.060t
2
)
k
^
m. Find the net force on the helicopter at t=3.4 s.
F
net
=(
i
^
+
j
^
+
k
^
kN
Answers
If the mass of the helicopter is m = 2.7 x 10⁴ kg and the position of the helicopter is given by the vector \(r(t) = 0.02t^3 \hat{i} + 2.2t \hat{j} - 0.06t^2 \hat{k}\), then the net force on the helicopter at t=3.4s is \(F_{net}= 1.1016 \hat{i} - 0.324 \hat{k}\) kN
To find the net force follow these steps:
The formula for force is F=m×a, where m is the mass and a is the acceleration. Since acceleration is rate of change of velocity and velocity is the rate of change of displacement, then acceleration= d²(r)/dt².So, the velocity, \(v(t) = \frac {dr}{dt} = 0.06t^2 \hat{i} + 2.2 \hat{j} - 0.12t \hat{k}\)m/s. Differentiating the velocity, we get acceleration, \(a(t) = \frac{dv}{dt} = 0.12t \hat{i} - 0.12 \hat{k}\). At t = 3.4s, the acceleration is, \(a(3.4) = 0.12(3.4) \hat{i} - 0.12 \hat{k} = 0.408\hat{i} - 0.12\hat{k}\) m/s²Therefore, the net force at time t=3.4, \(F_{net} = m \times a(3.4) \Rightarrow F_{net} = 2.7 \times [0.408 \hat{i} - 0.12 \hat{k}]= 1.1016 \hat{i} - 0.324 \hat{k}\) kNThus, the net force on the helicopter at t = 3.4 s is \(F_{net}= 1.1016 \hat{i} - 0.324 \hat{k}\) kN.
Learn more about vector:
brainly.com/question/27854247
#SPJ11
Computer salespeople at a local store earn a $100 commission per computer for the first 5 computers they sell each month. For every additional computer they sell during that month, the commission per computer is 1.5 times the rate for the first five. Which of the following is the total commission earned by a salesperson who sells 8 computers in a month?
A. $190
B. $800
C. $950
D. $1,050
E. $1,200
Answers
Answer:
C
Step-by-step explanation:
500+450=950
Solve the following initial value problem for the function \(y(x)\).
\(
y^{\prime}=2 x y^2 \quad ; \quad y(1)=1 / 2
\)
Answers
The solution of the initial value problem y' = 2xy² ; y(1) = 1/2 is y(x) = -1/(x² - 3)
What is an initial value problem?An initial value problem is a differential equation that contains the initial values of the variables of the differential equation.
How to solve the initial value problem?Given the initial value problem
y' = 2xy² ; y(1) = 1/2
So, we solve the differential equation as follows
y' = 2xy²
dy/dx = 2xy²
Separing the variables, we have
dy/y² = 2xdx
Integrating both sides of the equation, we have
∫dy/y² = ∫2xdx
∫dy/y² = 2∫xdx
We know that ∫xⁿ = xⁿ⁺¹/(n + 1)
So, integrating the expressions, we have
y⁻²⁺¹/(-2 + 1) = 2x¹⁺¹/(1 + 1)
y⁻¹/(-1) = 2x²/2 + c
-y⁻¹ = x² + c
Given that y(1) = 1/2, substituting these into the equaqtion, we have
-y⁻¹ = x² + c
-(1/2)⁻¹ = 1² + c
-2 = 1 = c
c = -2 - 1
c = -3
So, -y⁻¹ = x² + c
-y⁻¹ = x² - 3
Dividing through by - 1, we have
y⁻¹ = -(x² - 3)
Taking the inverse of both sides, we have
y(x) = -1/(x² - 3)
So, y(x) = -1/(x² - 3)
Learn more about initial value problem here:
https://brainly.com/question/27181805
#SPJ1
A rectangular parking lot has an area of 1,650 square yards. The length of the parking lot is 55 yards. What is the width of the parking lot, in yards?
Answers
Answer:
w = 30 yd
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightEquality Properties
Multiplication Property of Equality Division Property of Equality Addition Property of Equality Subtraction Property of EqualityGeometry
Area of a Rectangle: A = lw
l is lengthw is widthStep-by-step explanation:
Step 1: Define
A = 1650 yd²
l = 55 yd
w = unknown
Step 2: Solve for w
Substitute in variables [Area of a Rectangle]: 1650 yd² = (55 yd)(w yd)[Division Property of Equality] Divide 55 yd on both sides: 30 yd = wRewrite: w = 30 ydBen drove 5.75 hours and then Jerry drove 3 hours their total distance is given by the expression below 106(5.75)+128(3)
Answers
Answer:
993.5
Step-by-step explanation:
106×5.75 +128×3
Find a counterexample to show that the given conjecture is false.
If n is a real number, then n³>n.
Answers
Let \(n=0\). Then \(0^3 = 0\) but 0 > 0 is a false statement.
Find the value of x. (4x + 12)° 64°
Answers
Answer:
C. 13Step-by-step explanation:
the angle of measure 4x + 12 and the angle of measure 64 are Vertically opposite angles then they are equal in measure
therefore
4x + 12 = 64
⇔ 4x = 64 - 12
⇔ 4x = 52
⇔ x = 52/4
⇔ x = 13
5/8 z + (-2.5) = 2.5 worded
Answers
Answer:
Step-by-step explanation:
2.5 subtracted from (5/8)th of z gives 2.5
describe the structure of the coordinates associated with specific radian measurements on the unit circle
Answers
The structure of the coordinates associated with specific radian measurements on the unit circle follows a distinct pattern. The x and y coordinates represents the cosine and sine values of the angle, respectively.
The unit circle is a circle with a radius of 1 unit, centered at the origin of a Cartesian coordinate system.
It is commonly used in trigonometry to relate angles to the coordinates on the circle.
When we measure an angle in radians on the unit circle, we can associate specific coordinates with that angle.
The x-coordinate of a point on the unit circle represents the cosine value of the angle, while the y-coordinate represents the sine value of the angle.
These coordinates follow a pattern based on the radian measurement.
For example, when the angle is 0 radians (or 0 degrees), the corresponding point on the unit circle is (1, 0), where the x-coordinate is 1 (cosine of 0) and the y-coordinate is 0 (sine of 0).
As the angle increases, the coordinates change accordingly. For instance, when the angle is π/2 radians (or 90 degrees), the point on the unit circle is (0, 1), where the x-coordinate is 0 (cosine of π/2) and the y-coordinate is 1 (sine of π/2).
This pattern continues as the angle increases or decreases, and the coordinates on the unit circle change accordingly.
By using trigonometric functions, we can determine the cosine and sine values of any given angle and associate them with the appropriate coordinates on the unit circle.
In summary, the structure of the coordinates associated with specific radian measurements on the unit circle follows a pattern where the x-coordinate represents the cosine value of the angle, and the y-coordinate represents the sine value of the angle.
Together, these coordinates create points on the unit circle that correspond to the given radian measurement.
Learn more about Cartesian coordinate system here:
https://brainly.com/question/4726772
#SPJ11
The table represents a linear function. WhT is the slope of the function?
Answers
Answer
The slope of the function is 5.
Step-by-step explanation:
What is the probability of either event occurring when you roll adie?Event A: Rolling a prime numberEvent B: Rolling a 4Express your answer as a simplified fraction.
Answers
Given:
Roll a die.
Required:
We need to find the probability of rolling a prime number and a number 4.
Explanation:
A)
A die has sic sides and is numbered from 1 to 6.
The sample space, S ={1,2,3,4,5,6}
Let A be the event of rolling a prime number.
Recall that a prime number is a whole number greater than 1 whose only factors are 1 and itself.
\(A=\lbrace2,3,5\rbrace\)\(n(A)=3\)The probability of rolling a prime number is P(A).
\(P(A)=\frac{n(A)}{n(S)}\)\(P(A)=\frac{3}{6}\)\(P(A)=\frac{1}{2}\)B)
Let B be the event of rolling a number 4.
\(B=\lbrace4\rbrace\)\(n(B)=1\)The probability of rolling a number 4 is P(B).
\(P(B)=\frac{n(B)}{n(S)}\)\(P(B)=\frac{1}{6}\)Final answer:
The probability of rolling a prime number is 1/2.
The probability of rolling a 4 is 1/6.
Assuming it is a normal 6-sided die.
We have 6 possible possibilities : 1,2,3,4,5,6.
In these 6 numbers, only 2,3 and 5 are prime numbers.
Therefore, the probability of event A = 3/6 = 1/2.
There is only one 4 in this sample -> The probability of event B = 1/6.
What is the value of x in trapezoid ABCD?
x=15
x=20
x=45
X=60
Answers
Answer:
A. X = 15 is the correct answer.
Step-by-step explanation:
It's the only one that really makes sense.
Hope this helped :) :)
Answer:
15
Step-by-step explanation:
when a certain stretch of highway was rebuilt and straightened, the distance along the stretch was decreased by 20 percent and the speed limit was increased by 25 percent. by what percent was the driving time along this stretch reduced for a person who always drives at the speed limit?
Answers
The driving time along this stretch was reduced by 36% for a person who always drives at the speed limit.
To calculate the percent reduction in driving time along the stretch, we need to consider the effects of both the distance decrease and the speed increase.
First, let's assume the original distance of the stretch was D. After the reconstruction, the distance is now 0.8D (since it was decreased by 20%).
Next, let's assume the original speed limit was S. After the reconstruction, the speed limit is now 1.25S (since it was increased by 25%).
To calculate the original driving time along the stretch, we would use the formula: time = distance / speed. So the original driving time would be D/S.
After the reconstruction, the driving time would be (0.8D) / (1.25S) = 0.64D/S.
To calculate the percent reduction in driving time, we can use the formula: (original time - new time) / original time * 100%.
Plugging in the values we calculated, we get:
(original time - new time) / original time * 100% = (D/S - 0.64D/S) / (D/S) * 100% = 36%.
Know more about percent here:
https://brainly.com/question/28670903
#SPJ11
Identify the term that completes the equation.
Answers
Based on the right triangle altitude theorem, the term that completes the equation is: a. YZ.
What is the Right Triangle Altitude Theorem?The right triangle altitude theorem state that when an altitude is drawn to from the vertex of a right triangle to intersect the opposite side perpendicularly, the length of the altitude would be equal to the geometric mean of the line segments that are formed by the altitude on the right triangle's hypotenuse.
In other words, the square of the length of the altitude equals the product of the line segments formed, according to the right triangle altitude theorem.
XZ = altitude
WY = hypotenuse
WZ and YZ are the line segments formed.
Therefore, the equation would be:
XZ² = (WZ)(YZ) [right triangle altitude theorem]
Learn more about the right triangle altitude theorem on:
https://brainly.com/question/14357999
#SPJ1
A woman standing on a large rock at the edge of a lake is getting ready to swing from a rope that is tied to a branch that hangs over the water. The length of the rope the woman is holding is 7.3 m long. The woman hopes to land in the water at a point that is 13.7 m away from where she stands on the large rock. The angle between the point where the rope is tied and her landing spot in the water is 89°. What is the distance between the the point where the rope is tied and the point where she wants to land to the nearest tenth of a metre.
Answers
Answer:
6.4 m
Step-by-step explanation:
The image attached is a representation of the question. to the river hence the distance between the place where she landed and the rock where she was standing must be horizontal. We are now required to find the shortest vertical distance between the point where the rope was tied and the place where she wants to land.
Note that the woman used the rope to move down in
Applying the cosine rule;
\(c^{2} = a^{2} + b^{2} -2ab Cos C\)
\(c^{2} = 13.7^{2} + 7.3^{2} - 2(13.7 *7.3) Cos 89o\)
\(c^{2} = 6.4 m\)
Of the 1,400 students enrolled at a Middle School, 40% of students enrolled are in the 6th grade. How many students are enrolled in 6th grade? Explain how you got your answer.
Answers
Answer:
560 students
Step-by-step explanation:
1400*.40=560 students in 6th grade
Can someone help me with this one
Answers
For each question below, determine True or False: If a simple random sample is chosen with replacement, each individual has
the same chance of selection on every draw.
Answers
The statement If a simple random sample is chosen with replacement, each individual has the same chance of selection on every draw is True.
If a simple random sample is chosen with replacement, it means that after each selection, the chosen individual is placed back into the population before the next selection is made. In this case, each individual in the population has the same chance of being selected for every draw.
The process of replacing the selected individual ensures that the selection probabilities remain constant throughout the sampling process. As a result, each individual has an equal probability of being chosen on each draw, making the statement true.
To learn more about the simple random sample
https://brainly.com/question/30391235
#SPJ11
Solve for p.
98 = 4p + 38
Answers
Answer:
P=15
Step-by-step explanation:
Answer:
P=15
Step-by-step explanation:
first:
98-38=60
4p=60
60÷4=15
P=15
hope that helped :)