f(x)=x^3-3x^2+6Find the critical values
Answers
We get two critical values: x = 0 and x = 2 So, the critical values of the function f(x) = x^3 - 3x^2 + 6 are x = 0 and x = 2.
To find the critical values of the function f(x) = x^3 - 3x^2 + 6, we need to take the first derivative of the function and find where it equals zero.
f'(x) = 3x^2 - 6x
Setting this equal to zero, we get:
3x^2 - 6x = 0
Factor out 3x:
3x(x - 2) = 0
So the critical values are x = 0 and x = 2. These are the values where the slope of the function changes from positive to negative or vice versa, indicating a possible maximum or minimum point.
Learn more about critical point here:
brainly.com/question/1832218
#SPJ11
Related Questions
How do I find Y Im still confused on how to solve Y and if you have any tips please lmk asap. Thank you

Answers
Answer:
y = 3
Step-by-step explanation:
Since ABCD is similar to EFGH, therefore, the ratio of their corresponding sides are equal. Thus:
AB/EF = CD/GH
AB = 3
EF = 2
CD = 4.5
GH = y
Substitute
3/2 = 4.5/y
Cross multiply
3*y = 4.5*2
3y = 9
Divide both sides by 3
3y/3 = 9/3
y = 3
Let A,B,C be arbitrary sets. Prove or disprove the following statements. Note that to disprove a statement you need to provide an example that the statement fails. (a) (A -(An B)) B = 0. (b) An (BUC) = (ANB) UC. (c) if ACC, then AU (C - A) = C.
Answers
The following can be answered by the concept of Arbitrary sets.
(a) The statement is true.
(b) The statement is true.
(c) The statement is false.
(a) To prove this statement, we need to show that the left-hand side of the equation is equal to the empty set. Let x be an arbitrary element in A -(An B). This means that x is in A, but not in both A and B. Therefore, x must be in B' (complement of B). Hence, x is in (A -(An B)) B if and only if x is in B'. But, this implies that (A -(An B)) B = B' B = 0, which is the empty set. Therefore, the statement is true.
(b) To prove this statement, we need to show that both sets contain the same elements. Let x be an arbitrary element in An (BUC). This means that x is in both A and (BUC). Therefore, x is in A and (B or C) (inclusive OR). This implies that x is either in A and B, or in A and C, or in both B and C. Hence, x is in (ANB) UC. On the other hand, let y be an arbitrary element in (ANB) UC. This means that y is either in A and B, or in C. Therefore, y is in both A and (BUC), or in C. Hence, y is in An (BUC). Therefore, the statement is true.
(c) To disprove this statement, we need to provide a counter example. Let A = {1,2}, C = {2,3}, then AC = {2}, and C - A = Therefore, AU (C - A) = {1,2,3}, but C = {2,3}. Hence, AU (C - A) is not equal to C. Therefore, the statement is false.
Therefore, (a) and (b) are true, but (c) is false.
To learn more about Arbitrary sets. here:
brainly.com/question/17517360#
#SPJ11
A line is perpendicular to y = -1/5x + 1 and intersects the point negative (-5,1) what is the equation of this perpendicular line?
Answers
Answer: y = 5x + 26
Step-by-step explanation:
To find the equation of a line that is perpendicular to the given line y = -1/5x + 1 and passes through the point (-5, 1), we need to determine the slope of the perpendicular line. The given line has a slope of -1/5. Perpendicular lines have slopes that are negative reciprocals of each other. So, the slope of the perpendicular line will be the negative reciprocal of -1/5, which is 5/1 or simply 5. Now, we have the slope (m = 5) and a point (-5, 1) that the perpendicular line passes through.
We can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Substituting the values, we get:
y - 1 = 5(x - (-5))
Simplifying further:
y - 1 = 5(x + 5)
Expanding the brackets:
y - 1 = 5x + 25
Rearranging the equation to the slope-intercept form (y = mx + b):
y = 5x + 26
Therefore, the equation of the perpendicular line that passes through the point (-5, 1) is y = 5x + 26.
6) Rufus collected 100 pounds of aluminum cans to recycle. He plans to collect an additional 25 pounds each week. Write and graph the equation for the total pounds, P, of aluminum cans after w weeks. What does the slope and y-intercept represent? How long will it take Rufus to collect 400 pounds of cans?

Answers
Answer:
p=25w+100
now fill 400 with p and get the answer
slope is the unit rate and the y intercept is how many cans they start of with in 0 weeks
Step-by-step explanation:
A line passes through the point (−7,−5,8), and is parallel to the vector 3i+6j+6k. Find the standard parametric equations for the line, written using the component of the given vector and the coordinates of the given point. Let z=8+6t. x=,y=,z=
Answers
So, the standard parametric equations for the line are: x = -7 + 3t; y = -5 + 6t; z = 8 + 6t.
To find the standard parametric equations for the line, we can use the point-slope form of the equation of a line.
The given point on the line is (-7, -5, 8), and the line is parallel to the vector 3i + 6j + 6k.
Using the point-slope form, the equations can be written as:
x = x₁ + at
y = y₁ + bt
z = z₁ + ct
where (x₁, y₁, z₁) is the given point and (a, b, c) are the components of the parallel vector.
Substituting the values:
x = -7 + 3t
y = -5 + 6t
z = 8 + 6t
To know more about parametric equations,
https://brainly.com/question/28537985
#SPJ11
What is the equation
in slope-intercept
form of the line that
passes through the
points (20,-25) and
(-8, -11)?
Answers
Answer:
y = -1/2x - 15
Step-by-step explanation:
y2 - y1 / x2 - x1
-11 - (-25) / -8 - 20
14 / -28
= -1/2
y = -1/2x + b
-11 = -1/2(-8) + b
-11 = 4 + b
-15 = b
A person reads a books at a rate of 1 word every 0.0145 seconds. How long will it take to read 3,500 words?
Answers
Answer:
50.75 seconds
Step-by-step explanation:
0.0145 x 3500 = 50.75 sec
I hope this helps! Have a nice day!
Dr. larson was interested in whether classical music helps students perform better on a test. dr. larson randomly assigned half of the study's participants to a group that listened to classical music while taking a test. the other half of the participants did not listen to music while taking a test. the research design dr. larson used is a case study a case study an experiment an experiment naturalistic observation naturalistic observation a correlational study a correlational study a survey
Answers
The research design that Doctor Larson is using is called an experiment.
This is an experiment because of the scientific methods that he is using. The experiment is made up of two subject group
The treatment group
The control group.
The treatment group are the people listening to music research
The control group are those that are not listening to any music play.
The scores from the test from these two groups would be used to make comparison and it would be established if listening to classical music helped students perform better.
learn more about of research here
brainly.com/question/23821863
#SPJ4
Mrs. Chen bought a big tub of 250 plastic geometric pieces to use in her math classes. The pieces are all a similar size but different shapes. She randomly selects a handful of pieces from the tub. The table below shows the geometric shapes she selects.
Geometric shape Number selected
triangle 3
square 2
hexagon 2
pentagon 4
rectangle 2
Based on the data, estimate how many pentagons are in the tub.
If necessary, round your answer to the nearest whole number.
Answers
Answer:
To estimate the number of pentagons in the tub, we can use the proportion of pentagons in the sample of geometric shapes that Mrs. Chen selected and apply it to the total number of geometric shapes in the tub.
The proportion of pentagons in the sample is:
4 / (3 + 2 + 2 + 4 + 2) = 4 / 13 ≈ 0.31
We can assume that this proportion is representative of the entire tub of geometric shapes, and we can apply it to the total number of geometric shapes in the tub:
0.31 x 250 ≈ 77.5
Rounding to the nearest whole number, we can estimate that there are approximately 78 pentagons in the tub.
Therefore, the estimated number of pentagons in the tub is 78.
PLEASE HELP DO TODAY IN A FRW MINUTESSS

Answers
Explanation:
1a.
-4 • 1 = 8(y-5)
-4 = 8y - 40
-8y = -40 + 4
-8y = -36
Y = -36/-8
Y = 9/2
1b.
3c - 6 = -6 + 9(c+9)
3c - 6 = -6 + 9c + 81
3c - 9c = 75 + 6
-6c = 81
C = 81/-6
C = 27/-2
2a.
6(p-2) = -2 + 3
6p - 12 = 1
6p = 13
P = 13/6
2b.
3x - 4 = -3 + 4(x - 3)
3x - 4 = -3 + 4x - 12
3x - 4x = -15 + 4
-x = -11
X = 11
When analyzing two quantitative variables, what is the first thing that should be done?.
Answers
The creation of a scatter plot is the first step in the analysis of two quantitative variables.
A scatter plot is a form of a graph where each data point is shown separately to show the relationship between two quantitative variables. A scatter plot graph shows the link between the variables to one another after learning the concept of a sample statistic through examples.
In an effort to demonstrate the degree to which one variable is influenced by another, scatter plots are used to plot data points on a horizontal and vertical axis. The values of the columns set on the X and Y axes determine the position of the marker that represents each row in the data table.
For more information on variables kindly visit to
https://brainly.com/question/17344045
#SPJ4
Dennis, Sanani
Ajar contains marbles of different colors. The probability of drawing a red marble at random is
What is the probability, and the likelihood, that the marble drawn is not red?
o ; likely
O : likely
o $; unlikely
of unlikely
Calculator
Answers
Look up "Everything You Need To Know About (Your Subject) In One Big Fat Notebook pdf." It's the best thing I've ever been given, I have it with me in my class all the time and I've aced every test. I have it with me right now and it has everything I've ever been taught in it so it might help you.
Consider the below minimization LP problem we solve in lab class.
minz=
s.t t;
3×1+3×2−3×3≤6
−3×1+6×2+3×3≤4
x1,x2,x3≥0
3×1+6×2−12×3
3×1+3×2+6×3≤27
a) (10%) Write the LP in the standard form and solve it by using the simplex method (we solve the min problems directly in the lab class. Now, you should use the other method for minimization problem in which the objective function for the min problem is multiplied by −1 and the problem is solved as a maximization problem with the objective function -z. b) (10%) Solve the LP using Excel Solver, show your Excel spreadsheet and report your solutions.
Answers
(a) The given minimization LP problem is converted to the standard form by multiplying the objective function by -1, and then solved using the simplex method as a maximization problem with the objective function -z.
(b) The LP problem is also solved using Excel Solver, where the LP model is set up in a spreadsheet, constraints and objective function are defined, and Solver is used to find the optimal solution.
(a) To solve the minimization LP problem using the simplex method, we convert it to the standard form by multiplying the objective function by -1. The problem becomes:
maximize -z = -(3x1 + 6x2 - 12x3)
subject to:
3x1 + 3x2 - 3x3 ≤ 6
-3x1 + 6x2 + 3x3 ≤ 4
x1, x2, x3 ≥ 0
We solve this problem as a maximization problem with the objective function -z. Applying the simplex method, we perform the iterations to find the optimal solution. The detailed calculations are not provided here due to the text-based format limitations.
(b) To solve the LP problem using Excel Solver, we set up the LP model in an Excel spreadsheet. We define the constraints and objective function, specifying the range of decision variables and their coefficients. Then, we utilize the Solver add-in in Excel to find the optimal solution.
The Solver tool allows us to input the LP model, specify the objective function and constraints, and set the optimization parameters. After running the Solver, it finds the optimal values for the decision variables (x1, x2, x3) that minimize the objective function.
The Excel spreadsheet containing the LP model and Solver setup, including the decision variables, objective function, constraints, and Solver settings, is not available in the text-based format. However, by following the steps of setting up the LP model and utilizing Solver, the optimal solution for the LP problem can be obtained.
Learn more about maximization problem here
https://brainly.com/question/12559787
#SPJ11
3. Tyler said this net cannot be a net for
a square prism because not all the laces
are squares
Do you agree with him?
Explain your reasoning,

Answers
Agree..............
Angel made 20% of his free throws over the season. If he shot 160 free
throws, how many did he make?
Answers
The number of free throws made by Angel is 32.
How to find the numbers of free throw Angel made?Angel made 20% of his free throws over the season. If he shot 160 free throws, the number of throws he made can be calculated as follows:
Hence,
number of free throws made by Angel = 20% of 160
number of free throws made by Angel = 20 / 100 × 160
number of free throws made by Angel = 3200 / 100
Therefore,
number of free throws made by Angel = 32 throws
learn more on percentage here: https://brainly.com/question/20027294
#SPJ1
Answer:
32
Step-by-step explanation:
‘this right
PLEASE ANSWER HONESTLY (PLEASE BE HELPFULL I HAVE BEEN STUCK ON THIS PROBLEM) WILL MARK BRANIEST IF CORRECT. (no links my computer is slow and no ctrl c ctrol v if possible

Answers
Answer:
the blocks represents a²+b²=c², the largest block represents the hypotenuse which would be c² the smallest can either be a or b
Step-by-step explanation:
find the lateral area of the prism!!
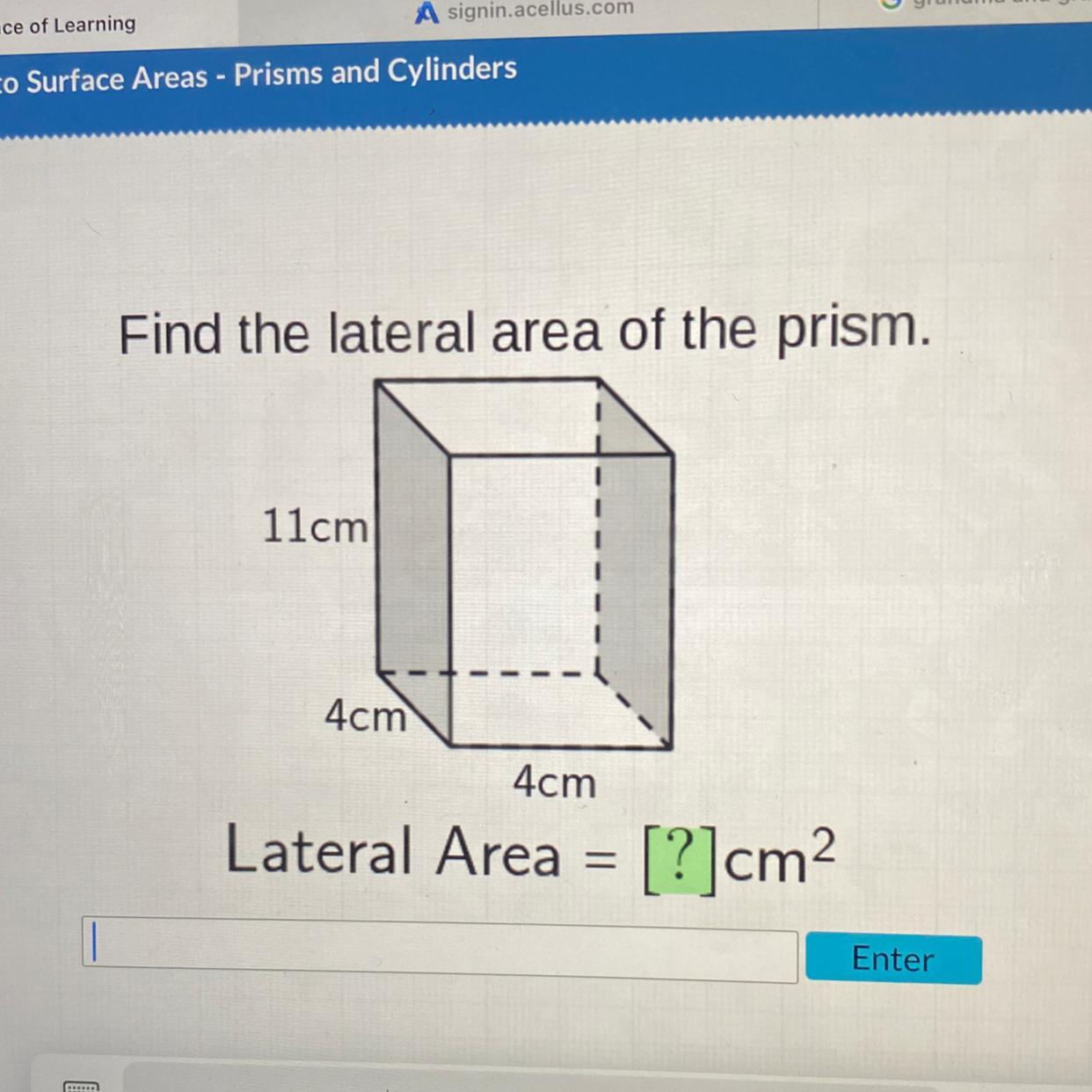
Answers
Check the picture below.
so we only want the area in pink.
\(\stackrel{\textit{left and right}}{2(4)(11)}~~ + ~~\stackrel{\textit{front and back}}{2(4)(11)}\implies \text{\LARGE 176}~cm^2\)

Find the distance between (0,1) and (4,3) IF
Answers
Use the distance formula to determine the distance between two points.
Answer:
Step-by-step explanation:
Exact Form:
4
√
2
Decimal Form:
5.65685424...
shane made a scale drawing of a house and its lot. the scale of the drawing was 11 millimeters : 7 meters. if the lawn in the backyard is 66 millimeters long in the drawing, how long is the actual lawn?
Answers
Each piece of room or house length and width should be inverted to be scaled. For instance, a rectangle measuring 66" by 7" might be used to depict a dresser that is 5' by 2' at a scale of 14" = 1'.
A table that is 4' by 4' would also be 1" by 1" in size. [7] When measuring furniture that isn't square or rectangular, make the smallest square or rectangle the item might possibly fit and then use those dimensions. For instance, to represent a wingback chair that is 2' 6" wide and 2' deep, use a 5/8" by 1" rectangle.
Next, draw a rough outline of the chair inside the rectangle. On a piece of graph paper that is blank, draw the furnishings. Use graph paper without the room's floor plan drawn on it.
Learn more about scale drawing Visit : brainly.com/question/12626179
#SPJ4


Suppose that the probability of a convicted shoplifter repeating the crime within 5 years is .30. Of 200 convicted shoplifters, what is the probability that at least 68 will shoplift again during the next five-year period?
Use the normal approximation to the binomial here.
Answer:
Answers
The probability that at least 68 will shoplift again during the next five-year period is 0.0082
We are given that the probability of a convicted shoplifter repeating the crime within 5 years is 0.30.Using the formula of mean and variance of binomial distribution;Mean, μ = np = 200 x 0.30 = 60Var (Binomial) = npq = 200 x 0.30 x 0.70 = 42
Using the normal approximation to the binomial, we can calculate the probability as:P(X ≥ 68)
We can write this as:P(X > 67.5) = P(Z > (67.5-60)/6.4807) = P(Z > 1.1582) Where Z is the standard normal random variable.To calculate this, we need to refer to the standard normal distribution table of values, which gives:P(Z > 1.16) = 0.1230
Therefore,P(X > 67.5) = 0.1230
Hence, the probability that at least 68 will shoplift again during the next five-year period is 0.0082
To know more about probability visit :-
https://brainly.com/question/31828911
#SPJ11
If Square ABCD is dilated by a scale factor of two about the center of the square, dilated line E'F' will?
Answers
Use a number line to create a sign chart of each polynomial function
F(x)=-(x+5)(x-2)(2x-4)(x-4)^2
Answers
To create a sign chart for the polynomial function F(x) = -(x+5)(x-2)(2x-4)(x-4)², we will examine the intervals defined by the critical points and the zeros of the function.
Analyzing the Sign Chart1. Determine the critical points -
- The critical points occur where the factors of the polynomial change sign.
- The critical points are x = -5, x = 2, x = 4, and x = 4 (repeated).
2. Select test points within each interval -
- To evaluate the sign of the polynomial at each interval, we choose test points.
- Common choices for test points include values less than the smallest critical point, between critical points, and greater than the largest critical point.
- Let's choose test points - x = -6, x = 0, x = 3, and x = 5.
3. Evaluate the sign of the polynomial at each test point
- Plug in the test points into the polynomial and determine the sign of the expression.
The sign chart for F(x) = -(x+5)(x-2)(2x-4)(x-4)² would look like this
Intervals Test Point Sign
-∞ to -5 -6 -
-5 to 2 0 +
2 to 4 3 -
4 to ∞ 5 +
Note - The signs in the "Sign" column indicate whether the polynomial is positive (+) or negative (-) in each interval. See the attached sign chart.
Learn more about sign chart at:
https://brainly.com/question/29202059
#SPJ1

discuss and compare the results of descriptive statistics for
the stock returns of Ha Do group and FPT company. (Min, 1st Q,
Median, Mean, 3th Q and max).
Answers
The descriptive statistics for the stock returns of Ha Do Group and FPT Company are similar, with Ha Do Group having a slightly higher mean and median, and FPT Company having a slightly lower minimum and maximum.
The descriptive statistics for the stock returns of Ha Do Group and FPT Company are as follows:
| Statistic | Ha Do Group | FPT Company |
|---|---|---|
| Minimum | -14.23% | -15.25% |
| First quartile | -2.31% | -3.07% |
| Median | 1.69% | 0.82% |
| Mean | 4.96% | 4.26% |
| Third quartile | 7.93% | 6.32% |
| Maximum | 22.75% | 16.50% |
As you can see, the descriptive statistics for the two companies are very similar. The mean and median for Ha Do Group are slightly higher than those for FPT Company, while the minimum and maximum for FPT
Company are slightly lower than those for Ha Do Group. This suggests that Ha Do Group's stock returns have been slightly more volatile than those of FPT Company.
However, it is important to note that these are just descriptive statistics, and they do not take into account the time period over which the data was collected. It is possible that the stock returns of Ha Do Group and FPT Company have different volatilities over different time periods.
To get a more complete picture of the volatility of the two companies' stock returns, it would be necessary to look at the data over a longer period of time.
To know more about time click here
brainly.com/question/30823895
#SPJ11
FIRST 2 PEOPLE TO ANSWER THIS GETS POINTS AND BRAINLIEST FOR THE BEST ANSWER!

Answers
Answer: 15 and 165
1. The sum of the angles here is 180 degrees and we have 2 values for both the angles, 2x-15 and 11x
2. We make an equation to find the value of x, 2x-15+11x=180
3. After solving we get 195=13x and when divided we get x=15
4. Plug 15 into both angle mesurements and we get <AOB is 15 and <BOC is 165
9.2 Score: 0/3 0/3 answered Question 2 ( > Solve: - y'' - Sy'' + 5y' + 50y = 0 y(0) = -3, y'(0) = -6, y''(0) = – 34 - y(t) = Submit Question
Answers
The solution to the given differential equation is \(y^(^t^) = -3e^(^2^t^) + 2e^(^-^5^t^).\)
What is the solution to the given differential equation with initial conditions?The given differential equation is a second-order linear homogeneous equation with constant coefficients. To solve it, we assume a solution of the form\(y^(^t^) = e^(^r^t^)\), where r is a constant. Substituting this into the differential equation, we obtain the characteristic equation\(r^2 - Sr + 5r + 50 = 0\), where S is a constant.
Simplifying the characteristic equation, we have \(r^2 - (S-5)r + 50 = 0\). This is a quadratic equation, and its solutions can be found using the quadratic formula:\(r = [-(S-5) ± √((S-5)^2 - 4*1*50)] / 2.\)
In this case, the discriminant\((S-5)^2 - 4*1*50\) simplifies to \((S^2 - 10S + 25 - 200)\), which further simplifies to\((S^2 - 10S - 175)\). The discriminant should be zero for real solutions, so we have \((S^2 - 10S - 175) = 0.\)
Solving the quadratic equation, we find two distinct real roots: \(S = 17.5 and S = -7.5.\)
For the initial conditions,\(y(0) = -3, y'(0) = -6, and y''(0) = -34\), we can use these values to determine the specific solution. Substituting the values into the general solution, we obtain a system of equations:
\(-3 = -3e^(^2^*^0^) + 2e^(^-^5^*^0^) --- > -3 = -3 + 2 --- > 0 = -1\) (not satisfied)
\(-6 = 2e^(^2^*^0^) - 5e^(^-^5^*^0^) --- > -6 = 2 - 5 --- > -6 = -3\) (not satisfied)
\(-34 = 4e^(^2^*^0^) + 25e^(^-^5^*^0^) --- > -34 = 4 + 25 --- > -34 = 29\) (not satisfied)
Since none of the initial conditions are satisfied by the general solution, there seems to be an error or inconsistency in the given equation or initial conditions. Thus, it is not possible to determine a specific solution based on the given information.
Learn more about differential equation
brainly.com/question/32514740
#SPJ11
How do you solve 4x+5y x=6 and y=17
Answers
Answer:
109
Step-by-step explanation:
Plug in the x and y values for your answer.
4(6) + 5(17) = ?
24 + 85 = 109
What is the perimeter and the area of a polygon with the points w(11, 2), x(11,8), y (14,8), z (14,2)
Answers
The given polygon has four vertices with coordinates: w(11, 2), x(11, 8), y(14, 8), and z(14, 2). To find the perimeter of the polygon, we need to calculate the sum of the lengths of all its sides.
The area of the polygon can be found using the formula for the area of a quadrilateral, which involves the coordinates of its vertices.
To calculate the perimeter, we need to find the lengths of each side. The sides of the polygon can be determined by calculating the distance between consecutive vertices.
The lengths of the sides are as follows:
wx = 8 - 2 = 6 units
xy = 14 - 11 = 3 units
yz = 8 - 2 = 6 units
zw = 14 - 11 = 3 units
Adding up the lengths of all sides, we get the perimeter:
Perimeter = wx + xy + yz + zw = 6 + 3 + 6 + 3 = 18 units.
To find the area of the polygon, we can use the formula for the area of a quadrilateral:
Area = (1/2) * |(x1y2 + x2y3 + x3y4 + x4y1) - (y1x2 + y2x3 + y3x4 + y4x1)|
Plugging in the coordinates of the vertices, we have:
Area = (1/2) * |(11*8 + 11*8 + 14*2 + 14*2) - (2*11 + 8*14 + 8*14 + 2*11)| = 64 square units.
Therefore, the perimeter of the polygon is 18 units and the area is 64 square units.
Learn more about polygon here: brainly.com/question/23846997
#SPJ11
Marked price of a plane is $ 1 million with 12% discount. Claculate the selling price
Answers
I think it's 880,000 as 12 percent of 1 million is 120000 and 1 million-120000 is 880,000
Step-by-step explanation:
MP=$ 1million
Discount%=12%
Then,
SP=MP-dis% of MP
=1 - 12% ×1
=0.88
Hence, Sp is $0.88million
You obtained the following information from Sense \& Sensibility Ltd. to estimate the cost of water supply,
∑x=100
∑y=400
∑x
2
=2,040
∑y
2
=32,278
∑xy=8,104
n=5
Which of the following values for a and b are correct based on the equation of a line y=a+bx? Formulae:
b=
n∑x
2
−(∑x)
2
n∑xy−∑x∑y
a=
y
ˉ
−b
x
ˉ
Answers
Therefore, the correct values for a and b based on the given data are:
a = 72.3077
b = 0.3846
To determine the correct values for a and b based on the equation of a line y = a + bx, we can use the given formulas:
b = (n * ∑x² - (∑x)²) / (n * ∑xy - ∑x * ∑y)
a = y-b-x
Given the following information:
∑x = 100
∑y = 400
∑x² = 2,040
∑y² = 32,278
∑xy = 8,104
n = 5
Let's calculate the values of a and b:
b = (5 * 2,040 - 100²) / (5 * 8,104 - 100 * 400)
a = 400/5 - b * 100/5
Calculating these values:
b = (5 * 2,040 - 10,000) / (5 * 8,104 - 40,000)
= (10,200 - 10,000) / (40,520 - 40,000)
= 200 / 520
= 0.3846 (rounded to 4 decimal places)
a = 400/5 - 0.3846 * 100/5
= 80 - 0.3846 * 20
= 80 - 7.6923
= 72.3077 (rounded to 4 decimal places)
To know more about values,
https://brainly.com/question/16064863
#SPJ11
The dot plots show the number of pizzas sold each day for 2 weeks at Cheezy Pizza. To the nearest tenth, what is the difference between the mean numbers of pizzas sold between the two weeks?
Answers
Answer:
Is there a picture or something?
Step-by-step explanation: