Given: A = (1, -6) B=(10,-4) Find: squr. 3*AB
Answers
Answer:
squr. 39
Step-by-step explanation:
See attached graph.
Form a right triangles and determine the length of the two sides (BC and AC). Then calculate the hypotenuse (AB) with the Pythagorean Theorem.
AB = 13
I'm not sure what "squr.3AB really means. 3AB is 39. The square root of 39 is 6.4, if square root is what is meant.

Related Questions
find the exact values of the sine, cosine, and tangent of the angle. 255° = 300° − 45°
Answers
The exact values of the sine, cosine, and tangent of the angle 255° are -1/√2, 1/√2, and -1, respectively.
To find the exact values of the sine, cosine, and tangent of the angle 255°, we can use the identity that relates the trigonometric functions of an angle to the trigonometric functions of its complement.
By expressing 255° as the sum of 300° and -45°, we can determine the exact values of the trigonometric functions for the given angle.
We know that the sine, cosine, and tangent of an angle are periodic functions, repeating every 360 degrees. To find the exact values of the trigonometric functions for 255°, we can express it as the sum of 300° and -45°, where 300° is a multiple of 360°.
Since the sine, cosine, and tangent functions are odd or even functions, we can use the values of the trigonometric functions for 45° to determine the values for -45°.
For 45°:
sin(45°) = cos(45°) = 1/√2
tan(45°) = 1
Since cosine is an even function, cos(-45°) = cos(45°) = 1/√2.
Since sine is an odd function, sin(-45°) = -sin(45°) = -1/√2.
Using the definition of tangent as the ratio of sine to cosine, tan(-45°) = sin(-45°) / cos(-45°) = (-1/√2) / (1/√2) = -1.
Therefore, for the angle 255°:
sin(255°) = -1/√2
cos(255°) = 1/√2
tan(255°) = -1
Learn more about trigonometric functions here:
brainly.com/question/28483432
#SPJ11
Evaluate if x = -2.
5-4x
Answers
Multiply: -4 times -2 equals 8
Subtract: 5-8=3
A random sample of size n1=27, taken from a normal population with a standard deviation σ1=6, has a mean x1=82. A second random sample of size n2=32, taken from a different normal population with a standard deviation σ2=4, has a mean x2=31. Find a 98% confidence interval for μ1−μ2.
Answers
The 98% confidence interval for μ1 - μ2 is approximately (47.847, 54.153).
To find a 98% confidence interval for μ1 - μ2 (the difference between the means of two populations), we can use the formula:
Confidence interval = (x1 - x2) ± Z * sqrt((σ1² / n1) + (σ2² / n2))
Where:
x1 and x2 are the sample means
σ1 and σ2 are the population standard deviations
n1 and n2 are the sample sizes
Z is the critical value corresponding to the desired confidence level
Given:
x1 = 82
x2 = 31
σ1 = 6
σ2 = 4
n1 = 27
n2 = 32
First, we need to find the critical value (Z) corresponding to a 98% confidence level. Since we want to find the two-sided confidence interval, we will use a significance level of (1 - confidence level)/2.
Using a standard normal distribution table or calculator, we find that the critical value for a 98% confidence level is approximately 2.33.
Now, we can calculate the confidence interval:
Confidence interval = (82 - 31) ± 2.33 * sqrt((6² / 27) + (4² / 32))
Confidence interval = 51 ± 2.33 * sqrt((36 / 27) + (16 / 32))
Confidence interval = 51 ± 2.33 * sqrt(1.333 + 0.5)
Confidence interval = 51 ± 2.33 * sqrt(1.833)
Confidence interval = 51 ± 2.33 * 1.354
Confidence interval = 51 ± 3.153
The 98% confidence interval for μ1 - μ2 is approximately (47.847, 54.153).
To know more about To find a 98% confidence interval for μ1 - μ2 (the difference between the means of two populations), we can use the formula:
Confidence interval = (x1 - x2) ± Z * sqrt((σ1² / n1) + (σ2² / n2))
Where:
x1 and x2 are the sample means
σ1 and σ2 are the population standard deviations
n1 and n2 are the sample sizes
Z is the critical value corresponding to the desired confidence level
Given:
x1 = 82
x2 = 31
σ1 = 6
σ2 = 4
n1 = 27
n2 = 32
First, we need to find the critical value (Z) corresponding to a 98% confidence level. Since we want to find the two-sided confidence interval, we will use a significance level of (1 - confidence level)/2.
Using a standard normal distribution table or calculator, we find that the critical value for a 98% confidence level is approximately 2.33.
Now, we can calculate the confidence interval:
Confidence interval = (82 - 31) ± 2.33 * sqrt((6² / 27) + (4² / 32))
Confidence interval = 51 ± 2.33 * sqrt((36 / 27) + (16 / 32))
Confidence interval = 51 ± 2.33 * sqrt(1.333 + 0.5)
Confidence interval = 51 ± 2.33 * sqrt(1.833)
Confidence interval = 51 ± 2.33 * 1.354
Confidence interval = 51 ± 3.153
To know more about confidence interval refer here:
https://brainly.com/question/32546207
#SPJ11
Solve (x + 2 < 5) u (x - 7 > -6).
{x | -6 < x < 5}
{x | x < 3 or x > 1}
{x | x < 0}
Answers
Given:
\((x+2<5)\cup (x-7>-6)\)
To find:
The solution for x.
Solution:
We have,
\((x+2<5)\cup (x-7>-6)\) ...(i)
Solve each inequality.
\(x+2<5\)
\(x<5-2\)
\(x<3\)
And,
\(x-7>-6\)
\(x>-6+7\)
\(x>1\)
It means (i) can be rewritten as
\((x<3)\cup (x>1)\)
We know that "∪" means solution of x<3 or x>1 both are included in the solution set.
Solution = {x | x<3 or x>1 }
Therefore, the correct option is B.
11. The scale of a dollhouse is l in: 2 ft. Which of the following would most likely be the measurement of the heightof the dollhouse's front doorA 21in2No - - -B. 3-Ft2O c. 14 inO D. 14H12. A flagpole casts a shadow 5 ft. long. At the same time, a 3 ft. yardstick casts a shadow 1.5 ft. long. How tall isthe flagpole?O A. 5 ft.B. 10 ft.O C. 20 ft.O D. 15 ft
Answers
We want to find the height of the dollhouse's front door.
Since the dollhouse's measures is given in inches, we have just two possible right choices:
because the answer should be given in inches.
If the correct option were the third one, 14 in,
then the real door measure would be twice in feet: 28 feet.
If the correct option were the first one, 3 1/2 in,
then the real door measure would be twice in feet: 7 in.
28 feet is a really big door. It is more likely for a house to have a 7 in door.
Answer: A. 3 1/2 in

Jon goes to a flea market and sells comic books for
3. dollars each. He starts the night with 20
dollars in his cash register. At the end of the night, he has 47
dollars in his cash register.
Answers
Since Jon sells comic books for 3 dollars each, we can divide the total amount of money he earned by the price of each comic book to find the number of comic books he sold:
27 dollars / 3 dollars per comic book = 9 comic books
Therefore, Jon sold 9 comic books during the night.
if x = 12 units and h = 8 units, then what is the area of the rhombus pictured above
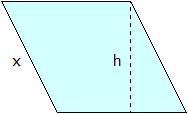
Answers
Answer:
a = 35.68 sq. units
Step-by-step explanation:
The area of a rhombus can be found by multiplying the lengths of its diagonals and dividing by 2:
Area = (diagonal 1 x diagonal 2) / 2
However, we are not given the diagonals of the rhombus. Instead, we are given that one of its sides, y, is 12 units, and its height, h, is 8 units.
Since a rhombus has four equal sides, we know that the length of the other side must also be 12 units. Therefore, the length of both diagonals of the rhombus can be found using the Pythagorean theorem:
diagonal = √(side^2 + height^2)
diagonal = √(12^2 + 8^2)
diagonal = √(144 + 64)
diagonal = √208
diagonal ≈ 14.4222 units
Now that we know the lengths of both diagonals, we can use the formula for the area of a rhombus:
Area = (diagonal 1 x diagonal 2) / 2
Area = (12 units x √208 units) / 2
Area ≈ 35.68 square units
Therefore, the area of the rhombus is approximately 35.68 square units.
To celebrate Halloween, Trisha's class is making candy necklaces. Trisha is helping pass out string from a 50-yard-spool. She gives 30 inches of string to each student. If there are 24 students in her class, how many yards of string will be leftover? 30 POINTS FOR CORRECT ANSWER
Answers
Answer:
30 yards of string will remain unused
Step-by-step explanation:
Ok, there are a lot of conversions going on here.
1 yard = 3 feet,
so 50 yards • 3ft per yard = 150 feet of string on the spool
1 foot = 12 inches,
so 150 feet • 12in per foot = 1800 inches of string on the spool
There are 24 students and they each get 30 inches, multiply 24 • 30 to see how much string is used:
24 • 30 = 720 inches of string used
Find how many inches of string is left by subtracting what is used from the original amount:
1800 - 720 = 1080 inches of spool left
To make this faster, instead of dividing by 12 inches per foot and then dividing by 3 feet per yard, I'm just dividing by 36 inches per yard.
1080 ÷ 36 = 30 yards of string remaining
There are 30 yards of the string that will be leftover.
What are Arithmetic operations?Arithmetic operations can also be specified by subtracting, dividing, and multiplying built-in functions.
The operator that performs the arithmetic operation is called the arithmetic operator.
* Multiplication operation: Multiplies values on either side of the operator
For example 4*2 = 8
/ Division operation: Divides left-hand operand by right-hand operand
For example 4/2 = 2
We have been given that Trisha gives 30 inches of string to each student.
∵ 1 yard = 3 feet,
∴ 50 yards = 150 feet of string on the spool
∵ 1 foot = 12 inches,
∴ 150 feet = 1800 inches of string on the spool
There are 24 students and they each get 30 inches,
So used inches of string :
⇒ 24×30 = 720
Now subtract the used string from the original amount:
⇒ 1800 - 720 = 1080 inches of spool left
So yards of string remaining = 1080/36 = 30.
Hence, there are 30 yards of the string that will be leftover.
Learn more about Arithmetic operations here:
brainly.com/question/25834626
#SPJ2
What is da answer my bruddas

Answers
Answer:
0.5
\(points \: of \: best \: fit \: are \\ (9, 5) \: and \: (1, 1) \\ slope = \frac{(1 - 5)}{(1 - 9)} \\ = \frac{ - 4}{ - 8} \\ = \frac{1}{2} \\ = 0.5\)
What is 13.5 rounded to the nearest whole
number?
Answers
The nearest whole number after rounding is, 14
What is Rounding of a number ?Rounding a number to the nearest tenth means finding the nearest multiple of 0.1.
To do this, you need to look at the digit in the hundredths place (the second digit after the decimal point) of the number you want to round.
If that digit is 5 or greater, you round the number up by adding 0.1 to the nearest whole number.
If that digit is 4 or less, you round the number down by leaving the nearest whole number unchanged.
For example, rounding 3.456 to the nearest tenth gives 3.5, while rounding 3.444 to the nearest tenth gives 3.4.
Given that,
The decimal number 13.5,
after using rules of rounding,
it can be rounded as 14
Hence, the nearest whole number is 14
To know more about Rounding check:
https://brainly.com/question/29878750
#SPJ9
When the scale factor is less than 1 The new image is?
Answers
The new image would be smaller in sample size than the original image.
For example, if the scale factor is 0.5, the new image will be half the size of the original image. To determine the exact size of the new image, the scale factor is multiplied with the width and height of the original image. For example, if the original image is 200 x 100 pixels, and the scale factor is 0.5, the new image will be
(200 x 0.5) = 100 x (100 x 0.5)
= 50 pixels.
The same concept applies when the scale factor is a decimal. For example, if the scale factor is 0.75, the new image will be three-quarters the size of the original image. In this case, the new image would be
(200 x 0.75) = 150 x (100 x 0.75)
= 75 pixels.
In summary, when the scale factor is less than 1, the new image will always be smaller than the original image, depending on the scale factor. The exact size of the new image can be determined by multiplying the width and height of the original image with the scale factor.
Learn more about sample size here
https://brainly.com/question/25894237
#SPJ4
Inverses, contrapositives and converses. Below are examples of mathematical statements you’ll encounter in this class. Assume x, y, a, b, c are integers.
If the difference x − y is even then x and y are also even.
If a divides b or a divides c then a divides bc. (Note: a divides b means that the fraction b/a is an integer. For example, 3 divides 6 but 3 does not divide 7.)
If x2 ≥ 100 and x ≥ 0, then x ≥ 10.
(i) (9 pts.) State the inverse, contrapositive and converse of each statement above. When possible, avoid using the word "not." Instead, replace "not even" with "odd", etc.
Recall that for P → Q,
contrapositive: ¬Q →¬P
converse: Q → P
inverse: ¬(P → Q) = ¬(¬P ∨ Q) = P ∧ ¬Q
(ii) (3 pts.) Then indicate their truth values. Thus, for each statement you must determine whether the statement itself, its inverse, contrapositive and converse are true or false. That’s four true/false answers for each statement.
Answers
1. Statement: True
Inverse: True
Contrapositive: True
Converse: True
2. Statement: True
Inverse: True
Contrapositive: True
Converse: True
3. Statement: True
Inverse: True
Contrapositive: True
Converse: True
(i)
Statement: If the difference x - y is even, then x and y are also even.
Inverse: If x and y are not even, then the difference x - y is not even.
Contrapositive: If x and y are not even, then the difference x - y is not even.
Converse: If x and y are even, then the difference x - y is even.
Statement: If a divides b or a divides c, then a divides bc.
Inverse: If a does not divide b and a does not divide c, then a does not divide bc.
Contrapositive: If a does not divide b and a does not divide c, then a does not divide bc.
Converse: If a divides bc, then a divides b or a divides c.
Statement: If x^2 ≥ 100 and x ≥ 0, then x ≥ 10.
Inverse: If x^2 < 100 or x < 0, then x < 10.
Contrapositive: If x^2 < 100 or x < 0, then x < 10.
Converse: If x ≥ 10, then x^2 ≥ 100.
(ii)
For each statement, we need to evaluate the truth values of the statement, inverse, contrapositive, and converse.
Statement: True
Inverse: True
Contrapositive: True
Converse: True
Statement: True
Inverse: True
Contrapositive: True
Converse: True
Statement: True
Inverse: True
Contrapositive: True
Converse: True
Learn more about statement from
https://brainly.com/question/24126971
#SPJ11
(Need this ASAP)In the problem below, which line contains an error?
Line 1: 6x – 2(x - 5) = 22
Line 2: 6x - 2x -10 = 22
Line 3: 4x -10 = 22
Line 4: 4x = 32
Line 5: x = 8
Answers
Mary baked 34 muffins on a Sunday. She gave 17 of them to her neighbor. Identify an equation and its solution that shows the number of muffins she had left.
Answers
X being the amount she has left :)
The equation is number of muffins left = 34 - 17 And the solution is number of muffins left = 17
Let's define the variables:
M = Number of muffins Mary baked originally (34 muffins)
G = Number of muffins given to her neighbour (17 muffins)
The equation that represents the number of muffins Mary had left after giving some to her neighbour is:
Number of muffins left = Original number of muffins - Number of muffins given
M - G
Substitute the values:
Number of muffins left = 34 - 17
Solving this equation:
Number of muffins left = 17
To know more about equation here
https://brainly.com/question/29657983
#SPJ3
Can someone please help me to do this question??

Answers
Answer:
Acute angles = less than 90°
∠1 Near D
∠2 Near B
∠3 Near D
∠2 Near E
∠1 Near A
Right angle = 90°
∠ECD
∠ECB
Adjacent angle pairs
∠1 and ∠3 Near A
∠4 and ∠2 Near A
∠3 and ∠1 Near D
∠2 and ∠4 Near D
∠2 Near B and ∠2 Near A
∠1 Near B and ∠1 Near A
∠4 Near D and ∠4 Near A
∠1 Near D and ∠4 Near A
∠2 Near E and ∠4 Near D
∠1 Near E and ∠4 Near A
Obtuse angle = Greater than 90°
∠2 Near D
∠1 Near E
∠4 Near D
This was a long one!
I hope this helped :)
5 and 9 are the example of ____ number
Answers
Answer:
Step-by-step explanation:
complex numbers , real numbers , rational numbers , natural numbers , whole numbers
0. Given a standard 4 color band resistor, what color code is needed on the 4 bands to have a 0.34
Ohm resistor with a tolerance of ± 10% ?
Answers
The colour code needed is silver, green, red and blue for the tolerance of ± 10% on the 4 color band resistor.
What is defined as the term resistor?A resistor is a device that controls or restricts how much electrical current can pass across a circuit in an electronic device. A specified voltage can be supplied via resistors to an active device like a transistor.For the given question;
The most popular type of resistor is the 4-band resistor. The first two bands just provide the first two digits of a resistance value, just as a three band resistor. For a 4 band resistor colour coding, we may start by first locating the tolerance band since it is typically gold or silver. The third band stands for the multiplier whereas the fourth band symbolises tolerance. Due to the widening difference between the tolerance band as well as the multiplier band, the tolerance band may also be easily distinguished.Since it is silver in this instance, the resistor colour code table indicates a tolerance of ± 10% .
Thus, the colour code needed is silver, green, red and blue for the 0.34
Ohm resistor with tolerance of ± 10%.
To know more about the resistor, here
https://brainly.com/question/24858512
#SPJ13
Determine if the given value is a solution of the inequality. Show your work.
7 – 2y > 3y + 13; y = -1
Answers
Given:
\(7-2y>3y+13\)
To find:
The whether the value \(y=-1\) is a solution of the given inequality or not.
Solution:
We have,
\(7-2y>3y+13\)
It can be rewritten as
\(-2y-3y>13-7\)
\(-5y>6\)
Divide both sides by -5 and change the inequality sign.
\(y<\dfrac{6}{-5}\)
\(y<-1.2\)
All the value of y less -1.2 are the solutions of the given inequality but -1 is greater than -1.2.
\(-1>-1.2\)
Therefore, \(y=-1\) is not a solution of the given inequality.
The equation Y+3=5(x-2)
goes through with point?
(2,-3)
(3,-2)
(-2,3)
(-3,2)
Answers
Answer:
(2, -3)
Step-by-step explanation:
Well the equation is y - y1 = m ( x - x1)
-3 = y1
2 = x1
(2, -3)
Answer:
(2,-3)
Step-by-step explanation:
The given equation is in point-slope form. That is,
\(y-y1=m(x-x1)\)
\(x1\) and \(y1\) is a point, while \(m\) is the slope.
So, \(y1=-3\) and \(x1=2\).
The point that this equation passes through is (2,-3).
I hope this helps!
What is the slope of the line graphed below?
th
(2, 3)
(1,-2)
Answers
Answer:
slope:5
Step-by-step explanation:
Answer: y = x + 5
Step-by-step explanation:
If it's perpendicular the slope is the opposite inverse of the other line,
The slope of line y = x + 5 is 1, because it's the number before x, so, the opposite inverse would be -1/1 = -1.
Part 4 It is the month for Reild trips and your school has decided to take Kindergarten students on a trip. to the Zoo The 200 is 160km away the driver is charging base on distance travelled for every 3km travelled, the cost is $50 for adults half this amount for students. Each fraction of 3km attracts the same cost. The trip consists of 30 students and there are s students to an adult 1) How many person in all are the bus?
Answers
It is the month for Reild trips and your school has decided to take Kindergarten students on a trip. The total number of people are 31.
What is the total number of people?Generally, To find the total number of people on the bus, we first need to determine the ratio of students to adults on the trip.
If there are s students to an adult, then the ratio of students to adults is s:1. If there are 30 students on the trip, then the total number of people on the trip is 30 + 1 = 31, since there are 30 students and 1 adult for every s student. So the total number of people on the bus is 31.
Read more about the total number
https://brainly.com/question/14993202
#SPJ1
i need help on this can you help??
" its geometry"

Answers
Both a square and a rhombus have equal-length sides. A rhombus only has its opposing angles equal, whereas a square has all of its angles at 90 degrees.
Describe the rhombus?
A parallelogram's special case is the rhombus. A rhombus has opposing sides that are parallel and opposing angles that are equal.
A rhombus also has equal-length sides on each side, and its diagonals split at right angles. A diamond or rhombus diamond is another name for the rhombus.
A square's diagonal lengths all have the same measurement. Several measurements are used to describe the diagonal lengths of rhombuses. While the square has four lines of symmetry, the rhombus only has two. Unlike a rhombus, which cannot be engraved in a circle, a square may be drawn inside of it.
Learn more about rhombus
brainly.com/question/27870968
#SPJ1
Adrian bought a car worth $12000 on 36 easy installments of $375. Answer the following questions. (1) How much total amount did Adrian pay in 36 months? Answer: Total payment A = $ (2) Identify the letters used in the simple interest formula I = Prt. I= $ P= $ and t years. (3) Find the rate of interest in percentage. Answer: r %. ASK YOUR TEACHER
Answers
3) since we don't have the information about the interest paid (I), we cannot determine the rate of interest at this time.
(1) To find the total amount Adrian paid in 36 months, we can multiply the monthly installment by the number of installments:
Total payment A = Monthly installment * Number of installments
= $375 * 36
= $13,500
Therefore, Adrian paid a total of $13,500 over the course of 36 months.
(2) In the simple interest formula I = Prt, the letters used represent the following variables:
I: Interest (the amount of interest paid)
P: Principal (the initial amount, or in this case, the car worth)
r: Rate of interest (expressed as a decimal)
t: Time (in years)
(3) To find the rate of interest in percentage, we need more information. The simple interest formula can be rearranged to solve for the rate of interest:
r = (I / Pt) * 100
To know more about Number visit:
brainly.com/question/3589540
#SPJ11
If 3 cats can kill 3 rats in 3 minutes, how long will it take 100 cats to kill 100 rats?
Answers
Answer:
an hour and 40 minutes.
or 100 minutes
Step-by-step explanation:
Answer:
3 minutes
lol
Give the intersection points of y=x the power of 5 and y=x the power of 7?
Answers
The intersection points of the function y = x⁵ and y = x⁷ are (0, 0) , (1, 1) and (-1 , -1).
In a plane, intersecting lines are any two or more lines that cross one another. The point of intersection, which can be found on all intersecting lines, is where the intersecting lines share a common point.
The equations are, y = x⁵ and y = x⁷
Equate both equation to each other, we get;
x⁷ = x⁵
Subtract x⁵ both sides , we get;
x⁷ - x⁵ = x⁵ - x⁵
x⁷ - x⁵ = 0
x⁵ (x² - 1) = 0
This gives two conditions;
x⁵ = 0
or, x² - 1 = 0
Solve both the equations as; x⁵ = 0
therefore, x = 0
And, x² - 1 = 0
( x - 1 ) (x + 1) = 0
x = 1 or x = -1
The values of x are 0 , 1 and -1
The intersection points For x = 0; y = x⁵ = 0
For x = 1; y = x⁵ = 1
For x = -1; y = x⁵ = -1
Thus, (0, 0), (1, 1), and (-1, -1) are the points where the functions y = x⁵ and y = x⁷ intersect.
Learn more about intersection points at:
brainly.com/question/14217061
#SPJ4
Help me please................

Answers
Answer:
≈1005
step by step explanation
= πr2(h)= π·82·5≈1005.30965
round -> 1005
Moe is 8 years older than Zach. If twenty years ago Moe was 3 times as old as Zach, what are their present ages.Moe: 32 Zach: 24Please include the steps taken to get the answer.
Answers
Moe's present age = 32
Zach's present age = 24
Explanations:Let Moe's present age be represented by m
Let Zach's present age be represented by z
Moe is 8 years older than Zach now
m = z + 8..........(1)
Twenty years ago, Moe's age would be m - 20
Twenty years ago, Zach's age would be z - 20
Twenty years ago, Moe's age was three times that of Zach
m - 20 = 3(z - 20)
m - 20 = 3z - 60
m = 3z - 60 + 20
m = 3z - 40..........(2)
Let equations (1) and (2) be equal to each other:
z + 8 = 3z - 40
3z - z = 8 + 40
2z = 48
z = 48 / 2
z = 24
Substitute the value of z into equation (1)
m = z + 8
m = 24 + 8
m = 32
Moe's present age = 32
Zach's present age = 24
maths uhhhhhhh?????????????????????????????

Answers
Answer: 68.852459016393 or 68.9 if you round up
Step-by-step explanation:
If you add all the students subjects together you get a total of 41. Then if you add up the total of students who study physics, chemistry, and both you get 20. Then I put those numbers is a percentage calculator then boom you got your answer.
How much power can be produced by a dam 150m tall, that has an efficiency of .90, and a flow rate of 15,000m^3/s? (p=npfgh)
Answers
The dam can produce approximately 197.1 MW of power.
What is the maximum power from dam with 150m height, 0.90 efficiency, 15,000m^3/s flow?The power (P) that can be produced by a dam can be calculated using the formula P = npfgh, where n is the efficiency, p is the density of the fluid (water), f is the flow rate, g is the acceleration due to gravity, and h is the height of the dam.
Given:
Height of the dam (h) = 150 m
Efficiency (n) = 0.90
Flow rate (f) = 15,000\(m^3\)/s
Acceleration due to gravity (g) = 9.8 m/\(s^2\)(approximate value for Earth)
Substituting these values into the formula, we have:
P = (0.90)(1000 kg/\(m^3\))(15,000 m\(^3/\)s)(9.8 m/\(s^2\))(150 m)
Calculating the expression:
P ≈ 197,100,000 Watts
Therefore, the dam has the potential to generate around 197.1 MW of power.
Learn more about power
brainly.com/question/29575208
#SPJ11
Someone please help me with the answer. ASAP

Answers
option a is the answer you are which class same question is there for me