Given C(2, −8), D(−6, 4), E(0, 4), U(1, −4), V(−3, 2), and W(0, 2), and that △CDE is the preimage of △UVW, represent the transformation algebraically.
Answers
Rotate triangle △C'D'E' counterclockwise by approximately -0.785 radians about the origin:
X₁ = 1 * cos(-0.785) - (-4) * sin(0.785) ≈ 0.436
y₁ = 1 * sin(-0.785) + (-4) * cos(0.785) ≈ -3.678
x₂ = -7 * cos(0.785) - 8
What is a triangle in its mathematical definition?
In geometry, a triangle is a three-sided polygon with three edges and three vertices. The most important property of triangles is that the sum of their interior angles equals 180 degrees.
Translation:
To translate a point (x, y) by a vector (h, k), we add h to the x-coordinate and k to the y-coordinate of the point.
To transform triangle △CDE to triangle △UVW, we can first translate triangle △CDE by a vector (h, k) to obtain triangle △C'D'E', where C' = C + (h, k), D' = D + (h, k), and E' = E + (h, k).
Since the coordinates of C are (2, -8) and the coordinates of U are (1, -4), we can calculate the translation vector (h, k) as follows:
h = 1 - 2 = - 1
k = -4 -(-8) = 4
So the translation vector is (-1 , 4)
Rotation:
To rotate a point (x, y) by an angle θ counterclockwise about the origin, we use the following formulas:
x' = x * cos(θ) - ytimes sinθ
y' = x * sin(θ) + y * cos(θ)
To transform triangle △C'D'E' to triangle △UVW, we can apply a rotation of angle θ counterclockwise about the origin to triangle △C'D'E', where C' = (x1', y1'), D' = (x2', y2'), and E' = (x3', y3'). Since the coordinates of C' are (2, -8) after translation, and the coordinates of U are (1, -4), we can calculate the rotation angle θ as follows:
θ = atan²(y₁ - y₂ , x₁ - x₂) - atan²(y₁ - y₂ , x₁ - x₂)
= atan²((-8 + 4) - (-4), (2 + 1) - (-6 + 3)) - atan²((-8) - (-4), 2 - (-6)
Using a calculator, we can find θ to be approximately -0.785 radians.
So, the algebraic representation of the transformation that maps triangle
ΔCDE to triangle ΔUVW
Translate triangle △CDE by the vector (-1, 4) to obtain triangle △C'D'E':
C' = (2 , -8) + (-1 , 4) = (1 , -4)
D' = (-6 , 4) + (-1 , 4) = (-7 , 8 )
E' = (0 ,4 ) + (-1 , 4 )
Therefore, Rotate triangle △C'D'E' counterclockwise by approximately -0.785 radians about the origin:
X₁ = 1 * cos(-0.785) - (-4) * sin(0.785) ≈ 0.436
y₁ = 1 * sin(-0.785) + (-4) * cos(0.785) ≈ -3.678
x₂ = -7 * cos(0.785) - 8
Learn more about triangle
brainly.com/question/2773823
#SPJ1
Related Questions
identify the graph that represents the given system of inequalities. also, identify two ordered pairs that are solutions to the system. y ≤ x 5 y ≤ 2x 3
Answers
Ordered pair (0, 6) and (2, 7) satisfy both inequalities in the system and are solutions to the system.
To identify the graph that represents the given system of inequalities y > x + 5 and y ≥ 2x + 3, we need to graph the individual inequalities and find the region where they overlap.
When we plot the graph of inequality separately:
y > x + 5:Draw a dashed line y = x + 5 (not including the line).Shade the region above the line.2. y ≥ 2x + 3:
Draw a solid line y = 2x + 3 (including the line).Shade the region above the line.The overlapping shaded region represents the solution to the system of inequalities.
To find two ordered pairs that are solutions to the system, we can choose any points within the overlapping region. Let's select two points:
Ordered pair 1: (0, 6)
Ordered pair 2: (2, 7)
These two points satisfy both inequalities in the system and are solutions to the system.
Learn more about inequalities;
https://brainly.com/question/30238989
#SPJ4
The correct question is given below -
Identify the graph that represents the given system of inequalities. Also identify two ordered pairs that are solutions to the system.
y > x + 5
y ≥ 2x + 3
what function creates a scatterplot and then adds a small amount of random noise to each point in the plot to make the points easier to find? 1 point the geom bar() function the geom smooth() function the geom point() function the geom jitter() function
Answers
To make the points in the scatterplot easier to find, the geom jitter() function method first builds a scatterplot and then adds a little amount of random noise to each point in the plot.
A scatterplot is produced using the ggplot2 function in R called geom jitter(). Each point in the plot receives a small bit of random noise to make them simpler to locate. The link between two variables in a dataset is visualised using this function.
The geom jitter() function can help to make data points easier to differentiate in a scatterplot by adding a small amount of random noise to each point. This is particularly useful when there is a lot of overlap between data points in the plot. The amount of jitter can be adjusted to ensure that the data points are still distinguishable, while still providing a more accurate representation of the data. Additionally, it can be used to adjust the size, color, and shape of the data points, allowing for a more customized visualization.
# Example of geom_jitter()
# Load ggplot2
library(ggplot2)
# Create data
x <- c(1,2,3,4,5,6,7,8,9,10)
y <- c(4,5,6,7,8,9,10,11,12,13)
# Plot data
ggplot(data = data.frame(x,y), aes(x, y)) +
geom_jitter()
Learn more about function here
https://brainly.com/question/29633660
#SPJ4
find the exact value of the expression, if it is defined. (if an answer is undefined, enter undefined.) tan−1 tan 6
Answers
The exact value of the expression, if it is defined for tan−1 tan 6 = tan 6 = 6 radians.
To discover the exact fee of the expression tan (tan 6), we want to understand the homes of inverse tangent and tangent features and their courting.
The tangent characteristic (tan^(-1) x) relates the ratio of the sine and cosine of an angle. It has a periodicity of π radians, this means that its values repeat after every π radians. In other phrases, tan (x + nπ) = tan x, in which n is an integer.
The inverse tangent characteristic (tan^(-1) x), also known as arctan or atan, is the inverse of the tangent function. It takes a ratio as input and returns the perspective whose tangent is that ratio.
Now, allow's to analyze the expression tan^(-1) (tan 6). Since 6 radians is inside the first duration of the tangent characteristic (0 to π radians), tan 6 is defined and falls within the variety of values for which the inverse tangent function is described.
Since tan^(-1) (tan 6) is the inverse of the tangent function carried out to the value of tan 6, we will count on the expression to simplify to the unique enter attitude, that's 6 radians.
To know more about trigonometry,
https://brainly.com/question/29766029
#SPJ1
1. what is the phase constant for the harmonic oscillator with the position function x(t) given in the plot if the position function has the form x(t)
Answers
The phase constant for the harmonic oscillator with the velocity function v(t), if the position function has the form x(t) = x_m cos(ωt + φ) is: -0.927 rad
How to find the Phase Constant?We are told that the vertical scale is set as: v_s = 4.0 cm/s
Using the formula of velocity, we can find the phase constant for the harmonic oscillator from the position function of form,
x(t) = x_m cos(ωt + φ)
The velocity of a body in motion is expressed as:
v = dx/dt -----(i)
Equation of displacement of the motion:
x(t) = x_m cos(ωt + φ) -----(ii)
Differentiating equation (ii), we get:
v = -v_m sin (ωt + φ) -----(iii)
Using the values of t = 0 s, v_m = 5 cm/s, v = 4 cm/s in equation (iii), we get:
4 = -5 sin (ω(0) + φ)
φ = sin⁻¹(4/5)
φ = -0.927 rad
Therefore, the phase constant for the harmonic oscillator with the velocity function v(t), if the position function has the form x(t) = x_m cos(ωt + φ) is -0.927 rad
Read more about Phase Constant at: https://brainly.com/question/30032263
#SPJ1
Complete question is:
What is the phase constant for the harmonic oscillator with the position function x(t) given in the plot if the position function has the form x = x_m cos(ωt + φ). The vertical axis scale is set as v_s = 4.0 cm/s

who is correct Alex or sophia and why?

Answers
Answer:
alex
Step-by-step explanation:
A. What is the slope of 2x-4y=4?
Answers

X=2y + 2 & here is a picture :)

plot the vector field. f(x, y) = x4, y4
Answers
This will produce a plot of the vector field for the function f(x,y) = x^4, y^4.
The vector field for f(x,y) = x^4, y^4 can be plotted by considering the gradient of the function, which gives us the direction and magnitude of the vector at each point (x,y).
The gradient of f(x,y) is given by:
grad(f) = (∂f/∂x)i + (∂f/∂y)j
= 4x^3 i + 4y^3 j
This tells us that at each point (x,y), the vector has a magnitude of sqrt((4x^3)^2 + (4y^3)^2) = 4sqrt(x^6 + y^6) and is pointing in the direction of (4x^3, 4y^3).
To plot the vector field, we can choose a set of points (x,y) on a grid and calculate the corresponding vectors. We can then draw an arrow at each point (x,y) with the length and direction given by the corresponding vector.
Alternatively, we can use software such as MATLAB or Python with a suitable library like matplotlib to plot the vector field. Here is an example code in Python:
import numpy as np
import matplotlib.pyplot as plt
# Define the vector field function
def f(x, y):
return np.array([x**4, y**4])
# Define the grid of points to plot
x = np.linspace(-1, 1, 20)
y = np.linspace(-1, 1, 20)
X, Y = np.meshgrid(x, y)
# Evaluate the vector field at each point
U, V = f(X, Y)
# Plot the vector field
plt.quiver(X, Y, U, V)
# Add labels and show the plot
plt.xlabel('x')
plt.ylabel('y')
plt.title('Vector Field for f(x,y) = x^4, y^4')
plt.show()
This will produce a plot of the vector field for the function f(x,y) = x^4, y^4.
Learn more about vector field here
https://brainly.com/question/31400700
#SPJ11
5.9At a specified point on a highway, vehicles are known to arrive according to a Poisson process. Vehicles are counted in 20-second intervals, and vehicle counts are taken in 120 of these time intervals. It is noted that no cars arrive in 18 of these 120 intervals. Approximate the number of these 120 intervals in which exactly three cars arrive.5.10 For the data collected in Problem 5.9, estimate the percentage of time headways that will be 10 seconds or greater and those that will be less than 6 seconds.
Answers
It can be deduced as the final answer that about 45.23% of the time headways are less than 6 seconds and about 4.06% of the time headways are 10 seconds or greater.
Using the Poisson distribution with the mean rate λ, we can solve for the probability of no cars arriving in 20 seconds, which is:
P(X = 0) = e^(-λ) = 18/120
Solving for λ, we get:
λ = -ln(18/120) = 0.6052
Then we can use the Poisson distribution again to solve for the probability of exactly three cars arriving in 20 seconds, which is:
P(X = 3) = (λ^3 / 3!) * e^(-λ) ≈ 0.1097
Finally, we can multiply this probability by the total number of 20-second intervals to estimate the number of intervals in which exactly three cars arrive:
0.1097 * 120 ≈ 13.16
Therefore, we can approximate that 13 of the 120 intervals will have exactly three cars arrive.
The headway between vehicles is the time gap between the arrivals of two consecutive vehicles. We can estimate the percentage of time headways that are 10 seconds or greater and those that are less than 6 seconds by using the exponential distribution with the same mean rate λ as in problem 5.9.
For a headway X, the probability density function of the exponential distribution is given by:
f(x) = λ * e^(-λx)
Therefore, the probability of a headway being less than 6 seconds is:
P(X < 6) = ∫[0,6] λ * e^(-λx) dx = 1 - e^(-6λ)
Similarly, the probability of a headway being 10 seconds or greater is:
P(X ≥ 10) = ∫[10,∞) λ * e^(-λx) dx = e^(-10λ)
Using the value of λ obtained in problem 5.9, we can estimate these probabilities as:
P(X < 6) ≈ 0.4523 or 45.23%
P(X ≥ 10) ≈ 0.0406 or 4.06%
Therefore, we estimate that about 45.23% of the time headways are less than 6 seconds and about 4.06% of the time headways are 10 seconds or greater.
Learn more about poisson's distribution here:-brainly.com/question/30388228
#SPJ11
The graph of f(x)= x is translated 3 units down to form the graph of g(x). Which of the following is g(x)
Answers :
A: g(x)= -3x
B: g(x)= 3x
C: g(x)= x - 3
D: g(x)= x + 3

Answers
Answer:
I'll edit the answer and try to answer it, but where is the graph?
Answer:
C: g(x)= x- 3
Step-by-step explanation:
translated 3 units down means you go 3 down on the y-axis. Therefore it is g(x)= x-3
solve for the inequality
-2+2x>-16
Answers
Sam ran 2 5/4 miles last weekend. This weekend he ran 3 5/1 miles. How many miles did he run in all?
Answers
Answer:
11 1/4
Step-by-step explanation:
2 5/4 = 3 1/4
3 5/1 = 8
8 + 3 1/4 = 11 1/4
under what conditions might someone be more rational? multiple choice question when provided likelihoods as percentages. when provided probability information. when provided frequency information. when provided less information.
Answers
The condition under which someone becomes more rational is when someone provided probability information.
Probability gives information about the likelihood that something will occur. For instance, weather patterns are used by meteorologists to predict the possibility of rain. Probability theory is utilized in epidemiology to comprehend the connection between exposures and the risk of health outcomes.
Everyday existence heavily relies on probability. In the analysis of political strategies, the determination of blood types, sports and gaming strategies, purchasing or selling insurance, online shopping, and online games.
Thus, having knowledge about probability makes someone more rational.
To read more about probability, visit https://brainly.com/question/11234923
#SPJ4
Find the lateral area of the pyramid

Answers
Answer:
The lateral surface area of the given square-based pyramid is 74 in².
Step-by-step explanation:
The lateral surface area of a three-dimensional object is the total surface area excluding the area of the base(s), so the total area of the "sides".
Therefore, the lateral surface area of a square-based pyramid is the sum of the area of the four triangular sides.
The area of a triangle is half the product of its base and height.
Therefore, the formula for the lateral surface area (L.S.A.) of a square-based pyramid is:
\(\boxed{\begin{minipage}{6 cm}\underline{L.S.A. of a square-based pyramid}\\\\$\sf L.S.A.= 2 \cdot s \cdot \ell$\\\\where:\\ \phantom{ww}$\bullet$ $s$ is the base length. \\ \phantom{ww}$\bullet$ $\ell$ is the slant height.\\\end{minipage}}\)
From inspection of the given diagram:
\(\ell = \sf 7.4\;in\)\(s=\sf 5\;in\)Substitute the given values into the formula to calculate the L.S.A. of the given square-based pyramid:
\(\begin{aligned}\implies \sf L.S.A.&=\sf 2 \cdot 5 \; in \cdot 7.4 \; in\\&=\sf 10 \; in \cdot 7.4 \; in\\&=\sf 74 \; in^2\end{aligned}\)
Therefore, the lateral surface area is 74 in².
The lateral area of the pyramid is approximately 74square inches.
What defines a pyramid's horizontal side?
The triangular faces of the pyramid that converge at the apex are known as the lateral faces. These are the four triangles that encircle the square base in the provided net. As a result, the entire area of the four triangles makes up the pyramid's lateral surface area.
According to the given information:To find the lateral area of a pyramid, we need to find the sum of the areas of all the triangular faces except for the base. The lateral area formula for a pyramid is given by:Lateral area = 0.5 × Perimeter of base × Slant height where the slant height is the height of each triangular face.
First, let's find the perimeter of the base. Since the base is a square with a side length of 5.1 inches, its perimeter is:
Perimeter of base = 4 × Side length = 4 × 5.1 in = 20.4
In Next,
let's find the slant height. We can use the Pythagorean theorem to find the slant height of each triangular face.
The slant height is the hypotenuse of a right triangle with one leg equal to half the base length (since the base is a square) and the other leg equal to the height of the pyramid.
Half the base length = 5.1 in / 2 = 2.55
In Using the Pythagorean theorem, we get:Slant height = √(2.55² + 7²) ≈ 7.45 In Finally,
we can use the lateral area formula to find the lateral area of the pyramid:
Lateral area = 0.5 × Perimeter of base × Slant height= 0.5 × 20.4 in × 7.45 in≈ 76.02 in²
Therefore, the lateral area of the pyramid is approximately 76.02 square inches. Which is near to 74
To know more about lateral area of the pyramid visit:
https://brainly.com/question/9953526
#SPJ1
PQ= RQ and PS= RS a=?

Answers
The measure of angle a is 15 degrees and this can be determined by using the properties of the isosceles triangle.
What are interior angles?In geometry, interior angles are formed in two ways. One is inside a polygon, and the other is when parallel lines cut by a transversal. Angles are categorized into different types based on their measurements.
Given:
The length of the segment PQ is equal to the length of the segment RQ.The length of the segment PS is equal to the length of the segment RS.The following steps can be used in order to determine the measure of angle a:
Step 1 - According to the given data, it can be concluded that triangle PQR and triangle PSR are isosceles triangles.
Step 2 - Apply the sum of interior angle property on triangle PQR.
\(\angle\text{Q}+\angle\text{P}+\angle\text{R}=180\)
\(\angle\text{Q}+2\angle\text{R}=180\)
\(2\angle\text{R}=180-60\)
\(\angle\text{R}=60^\circ\)
Step 3 - Now, apply the sum of interior angle property on triangle PSR.
\(\angle\text{P}+\angle\text{S}+\angle\text{R}=180\)
\(\angle\text{S}+2\angle\text{R}=180\)
\(2\angle\text{R}=180-90\)
\(\angle\text{R}=45^\circ\)
Step 4 - Now, the measure of angle a is calculated as:
\(\angle\text{a}=60-45\)
\(\angle\text{a}=15\)
The measure of angle a is 15 degrees.
For more information on interior angles, refer to the link given below:
https://brainly.com/question/28795639
Which figure is the image of Q?


Answers
That’s the only one that rotated 90 degrees counterclockwise
Use properties of equality to solve the equation for w. You must show your work. 2(w+3) = −2(w−21)
Answers
Answer:
9
Step-by-step explanation:
2w+6=-2w+42
4w+6=42
4w=36
w=9
Answer:
Today: Friday, 06 November 2020
Hour: 19.17 WIB (Indonesia)
_______________________________
2 (w + 3) = -2(w - 21)
2w + 6 = -2w + 42
2w + 2w = -6 + 42
4w = 36
w = 9
we say that x and y form a chain of quadratic residues modulo p if x, y, and x y are all quadratic residues modulo p. (a) find a chain x, y and x y of quadratic residues modulo 11. (b) is there a chain of quadratic residues modulo 7?
Answers
(a) A chain of quadratic residues modulo 11 can be formed with x = 1, y = 3, and xy = 3, which are all quadratic residues modulo 11.
(b) There is no chain of quadratic residues modulo 7.
(a) To find a chain of quadratic residues modulo 11, we need to find values of x, y, and xy that are all quadratic residues modulo 11. We can try different values and check if they satisfy this condition. One possible chain is x = 1, y = 3, and xy = 3. Squaring each of these values modulo 11, we have 1^2 ≡ 1, 3^2 ≡ 9, and (1 × 3)^2 ≡ 3^2 ≡ 9. Therefore, x = 1, y = 3, and xy = 3 form a chain of quadratic residues modulo 11.
(b) To determine if there is a chain of quadratic residues modulo 7, we need to check if there exist x, y, and xy that are all quadratic residues modulo 7. We can try different values and observe their squares modulo 7. However, in this case, we find that there is no such chain. When we square numbers modulo 7, we have 0^2 ≡ 0, 1^2 ≡ 1, 2^2 ≡ 4, 3^2 ≡ 2, 4^2 ≡ 2, 5^2 ≡ 4, and 6^2 ≡ 1. Since the squares are not all distinct residues, it is not possible to form a chain of quadratic residues modulo 7.
Learn more about modulo : brainly.com/question/29262253
#SPJ11
determine whether or not the vector field is conservative. f(x,y) = 33x2y2i + 22x3yj
Answers
The vector field f(x,y) = 33x^2y^2i + 22x^3yj is conservative, and its potential function is φ(x,y) = 11x^3y^2 + 11x^2y^2 + C.
To determine if a vector field is conservative, we need to check if it is the gradient of a scalar function (i.e., a potential function). We can do this by taking the partial derivatives of each component with respect to their respective variables and checking if they are equal:
∂f_x/∂y = 66xy^2
∂f_y/∂x = 66xy^2
Since these partial derivatives are equal, the vector field is conservative. We can then find a potential function by integrating each component with respect to their respective variable:
φ(x,y) = 11x^3y^2 + 11x^2y^2 + C
where C is the constant of integration.
Therefore, the vector field f(x,y) = 33x^2y^2i + 22x^3yj is conservative, and its potential function is φ(x,y) = 11x^3y^2 + 11x^2y^2 + C.
Learn more about vector field
brainly.com/question/14122594
#SPJ11
What is the slope and y intercept of this graph? please explain.

Answers
Answer:
Slope=2
y-intercept=(-2)
Step-by-step explanation:
hope this helps :3
if it did pls mark brainliest
Answer:
The y-intercept is -2 and the slope is 2.
Step-by-step explanation:
rise over run lol
Please help me, I don’t understand
Polynomial: x4 + 2x³ - 3x² + x - 4; Divisor: x² + x + 1
Answers
Evaluate this exponential expression.
A. 63
OB. 66
C. 19
D. 207
6 (4+2)2-32
Answers
Answer:To evaluate the exponential expression 6(4+2)² - 32, we need to follow the order of operations, which is parentheses, exponents, multiplication and division (from left to right), and addition and subtraction (from left to right).
First, we simplify the expression inside the parentheses:
4 + 2 = 6
Next, we square the result:
6² = 36
Now, we substitute the squared result back into the expression:
6(36) - 32
Next, we perform the multiplication:
6 * 36 = 216
Finally, we subtract 32:
216 - 32 = 184
Therefore, the value of the given exponential expression 6(4+2)² - 32 is 184.
Look at the shapes and decide wheater to use (1) sine law(2) cosine law, or (3) SOHCAHTOA

Answers
The triangle ABC, the angle x is 36°.
Given that,
In the picture, we have triangles ABC.
We have to find the angle x.
The sides of the triangle are AB=3cm and AC=5cm.
We have the angle B is 90°.
We use the sine law.
In trigonometry, there are six fundamental ratios that are used to establish a connection between a right triangle's side-to-angle ratio and its angle. If the angle created by the base and hypotenuse of a right-angled triangle is, then
Perpendicular/hypotenuse = sin θ
base/hypotenuse = cos θ
tan θ = Base/Perpendicular
The three additional functions' values, cot, sec, and cosec, are dependent on the values of tan, cos, and sin, as shown below.
cot θ= perpendicular/base
sec θ=hypotenuse/base
cosec θ=hypotenuse/perpendicular
So,
Sin x=opposite side/hypothesis
Sin x=3/5
Sin x= 0.6
x= sin⁻¹(0.6)
x=36.86°
Approximately, x=36°
Therefore, The angle x is 36°.
To learn more about angle visit: https://brainly.com/question/28451077
#SPJ9
8 minus 5 divided by 1/2 multiplied by 2
Answers
Answer: -12
Step-by-step explanation: 8 - 5 / (1/2) * 2
We need to follow PEMDAS.
8 - 5 / (1/2) * 2
8 - 10 * 2
8 - 20
-12
Would appreciate brainly <3
Find the area of the triangle below.
Be sure to include the correct unit in your answer.
14 yd
15 yd
17 yd
Answers
Answer:
17 yd
Step-by-step explanation:
Cause why not?
Carry on learning:)
The best player on a basketball team makes
80% of all free throws. The second-best player makes
75% of all free throws. The third-best player makes
65% of all free throws. Based on their experimental probabilities, estimate the number of free throws each player will make in his or her next
80 attempts. Explain.
Answers
Expected number of free throws in 80 attempts:
Best player = 64
2nd best player = 60
3rd best player = 52
We have to given that,
The probability that best player makes free throw, p1 = 0.8
The probability that second-best player makes free throw, p2 = 0.75
The probability that third-best player makes free throw, p3 = 0.65
Here, Total number of attempts made in free throws, n = 80.
Since, The estimated number of free throws that any player makes is defined by:
E ( Xi ) = n × pi
Where, Xi = Player rank
pi = Player rank probability
Hence, Expected value for best player making the free throws would be:
E (X1) = n × p1
= 80 x 0.8
= 64 free throws
Expected value for second-best player making the free throws would be:
E (X2) = n*p2
= 80 x 0.75
= 60 free throws
Expected value for third-best player making the free throws would be:
E (X3) = n*p3
= 80 x 0.65
= 52 free throws
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ1
Name one pair of complementary angles. (1 point)
16. Name one pair of supplementary angles. (1 point)
17. Draw an angle that measures 95° and label it BAD. (2 points)
Use this diagram for questions 18 ‐ 23. (1 point each)
**The lines are PARALLEL**
18. Identify a pair of corresponding angles.
19. Identify a pair of alternate interior angles.
20. Identify a pair of alternate exterior angles.
21. Identify a pair of vertical angles.
22. If the measure of angle 2 is 35°, what is the measure of angle 6? 23. If the measure of angle 2 is 35°, what is the measure of angle 8?

Answers
Answer:
angle 7 and 8 are supplementry angle 7 and 6 are complementry. ANgle 2 and 7 are alternite exterior angles, andle 4 and 5 are alternite interior angles angles 1 and 4 are vertical angle 6 is 35. angle 8 is 135
Step-by-step explanation:
The diagram shows j // k and cut by transversal t. Which angle is a corresponding angle to Angle 8 in the diagram below?

Answers
The corresponding angle of angle 8 is angle 4.
How to find corresponding angles?When parallel lines are cross by a transversal line, angle relationships are formed such as corresponding angles, alternate interior angles, linear angles, same interior angles, alternate exterior angles, vertically opposite angles.
In the diagram, j and k are parallel line cut by the transversal t. Let's find the corresponding angle of 8.
Corresponding angles are the angles which are formed in matching corners with the transversal when two parallel lines are intersected by any other line. corresponding angles are congruent.
Therefore,
∠4 is corresponding to ∠8.
learn more on angles here: https://brainly.com/question/18015826
#SPJ1
PLEASE HELP
WILL GIVE BRAINLIEST

Answers
Answer:
1 1/3 or 4/3
Step-by-step explanation:
7 10/12 - 6 6/12 = 1 4/12
simplify.
1 1/3
Answer:
4/3 or 1 and 1/3
Step-by-step explanation:
First we need to make the fractions normal. We multiply 7 times 6 to get 42, then add 42 to 5 to get 47/6. Then we multiply 6 times 2 to get 12, then add 1 to that to get 13/2. Then we multiply both the 13 and the 2 by 3 to get 39/6. Then subtract 39 from 47, this gives us 8/6, we can then simplify this to get 4/3 or 1 and 1/3.
A card is picked at random from the following set. What is P(9) ? Write your answer as a percentage in the box given below.
Answers
Answer:
25%
Step-by-step explanation:
The (not mentioned in the question) set is: 6 7 8 9.
There are 4 total outcomes and only 1 favorable outcome, then the probability to pick a 9 is:
P(9) = favorable outcome/total outcomes
P(9) = 1/4 = 0.25 or 0.25*100 = 25%
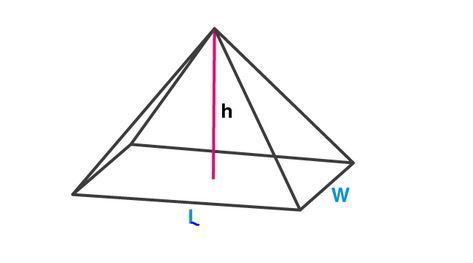
The base of the pyramid is a rectangle that is not a
square. Which statements correctly describe the
symmetry of the pyramid? Check all that apply.
The pyramid has four planes of symmetry.
O The pyramid has two planes of symmetry.
An axis of symmetry passes through the vertex and
is perpendicular to the base.
An axis of symmetry passes through the vertex and
through one of the triangular faces of the pyramid.
An angle that measures 90° is an angle of rotation
for an axis of symmetry for the pyramid.
An angle that measures 45° is an angle of rotation
for an axis of symmetry for the pyramid.
Answers
An axis of symmetry passes through the vertex and is perpendicular to the base. Then the correct options are B, C, and E.
What is a rectangular pyramid?Take a rectangle. This is the base. Now take 4 triangles such that each of them are connected to one-one side of the base rectangle and when they're taken together, they form a closed object. That shape is called rectangular pyramid.
The base of the pyramid is a rectangle that is not a square.
The pyramid has two planes of symmetry.
An axis of symmetry passes through the vertex and is perpendicular to the base.
An angle that measures 90° is an angle of rotation for an axis of symmetry for the pyramid.
Then the correct options are B, C, and E.
Learn more about rectangular pyramid here:
https://brainly.com/question/16261758
#SPJ1