Answers
Answer:
look at the photo..................

Related Questions
What is the product of 709 and 68?
Answers
Answer:
\(709*68=48212\)
ans = 48212
Ariana spends $24 every 6 days how much will she spend in 10 days
Answers
Which sequence of transformations was applied to the parent tangent function to create the function m(x) = 2tan(3x+4)
Answers
The function m(x) = 2tan(3x+4) is obtained by applying a sequence of transformations to the parent tangent function.
To determine the sequence of transformations, let's break down the given function:
1. Inside the tangent function, we have the expression (3x+4). This represents a horizontal compression and translation.
2. The coefficient 3 in front of x causes the function to compress horizontally by a factor of 1/3. This means that the period of the function is shortened to one-third of the parent tangent function's period.
3. The constant term 4 inside the parentheses shifts the function horizontally to the left by 4 units. So, the graph of the function is shifted to the left by 4 units.
4. Outside the tangent function, we have the coefficient 2. This represents a vertical stretch.
5. The coefficient 2 multiplies the output of the tangent function by 2, resulting in a vertical stretch. This means that the graph of the function is stretched vertically by a factor of 2.
In summary, the sequence of transformations applied to the parent tangent function to create the function m(x) = 2tan(3x+4) is a horizontal compression by a factor of 1/3, a horizontal shift to the left by 4 units, and a vertical stretch by a factor of 2.
Example:
Let's consider a point on the parent tangent function, such as (0,0), which lies on the x-axis.
After applying the transformations, the corresponding point on the function m(x) = 2tan(3x+4) would be:
(0,0) -> (0,0) (since there is no vertical shift in this case)
This example helps illustrate the effect of the transformations on the graph of the function.
For more question on expression
https://brainly.com/question/1859113
#SPJ8
need help with this ASAP
!!!!!!!!!!!!!!!!!!!!!!!!

Answers
The fence in dead center is about 399 feet from the third base.
What is the Pythagorean Theorem?The Pythagorean Theorem states that in the case of a right triangle, the square of the length of the hypotenuse, which is the longest side, is equals to the sum of the squares of the lengths of the other two sides.
Hence the equation for the theorem is given as follows:
c² = a² + b².
In which:
c > a and c > b is the length of the hypotenuse.a and b are the lengths of the other two sides (the legs) of the right-angled triangle.For the triangle in this problem, we have that:
The sides are d ft and 90 ft.The hypotenuse is of 409 ft.Hence the distance is obtained as follows:
d² + 90² = 409²
\(d = \sqrt{409^2 - 90^2}\)
d = 399 ft.
More can be learned about the Pythagorean Theorem at brainly.com/question/30203256
#SPJ1
Find constants a and b such that the function y = a sin(x) + b cos(x) satisfies the differential equation y'' + y' − 5y = sin(x).
Answers
Answers:
a = -6/37
b = -1/37
============================================================
Explanation:
Let's start things off by computing the derivatives we'll need
\(y = a\sin(x) + b\cos(x)\\\\y' = a\cos(x) - b\sin(x)\\\\y'' = -a\sin(x) - b\cos(x)\\\\\)
Apply substitution to get
\(y'' + y' - 5y = \sin(x)\\\\\left(-a\sin(x) - b\cos(x)\right) + \left(a\cos(x) - b\sin(x)\right) - 5\left(a\sin(x) + b\cos(x)\right) = \sin(x)\\\\-a\sin(x) - b\cos(x) + a\cos(x) - b\sin(x) - 5a\sin(x) - 5b\cos(x) = \sin(x)\\\\\left(-a\sin(x) - b\sin(x) - 5a\sin(x)\right) + \left(- b\cos(x) + a\cos(x) - 5b\cos(x)\right) = \sin(x)\\\\\left(-a - b - 5a\right)\sin(x) + \left(- b + a - 5b\right)\cos(x) = \sin(x)\\\\\left(-6a - b\right)\sin(x) + \left(a - 6b\right)\cos(x) = \sin(x)\\\\\)
I've factored things in such a way that we have something in the form Msin(x) + Ncos(x), where M and N are coefficients based on the constants a,b.
The right hand side is simply sin(x). So we want that cos(x) term to go away. To do so, we need the coefficient (a-6b) in front of that cosine to be zero
a-6b = 0
a = 6b
At the same time, we want the (-6a-b)sin(x) term to have its coefficient be 1. That way we simplify the left hand side to sin(x)
-6a -b = 1
-6(6b) - b = 1 .... plug in a = 6b
-36b - b = 1
-37b = 1
b = -1/37
Use this to find 'a'
a = 6b
a = 6(-1/37)
a = -6/37
Two containers designed to hold water are side by side, both in the shape of a
cylinder. Container A has a diameter of 10 feet and a height of 8 feet. Container B has
a diameter of 12 feet and a height of 6 feet. Container A is full of water and the water
is pumped into Container B until Container A is empty.
To the nearest tenth, what is the percent of Container B that is empty after the
pumping is complete?
Container A
play
Container B
10
d12
8
h6
O

Answers
Answer: Volume of Cylinder A is pi times the area of the base times the height
π r2 h = (3.1416)(4)(4)(15) = 753.98 ft3
Volume of Cylinder B is likewise pi times the area of the base times the height
π r2 h = (3.1416)(6)(6)(7) = 791.68 ft3
After pumping all of Cyl A into Cyl B
there will remain empty space in B 791.68 – 753.98 = 37.7 ft3
The percentage this empty space is
of the entire volume is 37.7 / 791.68 = 0.0476 which is 4.8% when rounded to the nearest tenth
.
Step-by-step explanation: I hope that help you.
Note: you may not need to type in the percent sign.
===========================================================
Explanation:
Let's find the volume of water in container A.
Use the cylinder volume formula to get
V = pi*r^2*h
V = pi*5^2*8
V = 200pi
The full capacity of tank A is 200pi cubic feet, and this is the amount of water in the tank since it's completely full.
We have 200pi cubic feet of water transfer to tank B. We'll keep this value in mind for later.
-----------------------
Now find the volume of cylinder B
V = pi*r^2*h
V = pi*6^2*6
V = 216pi
Despite being shorter, tank B can hold more water (since it's more wider).
-----------------------
Now divide the results of each section
(200pi)/(216pi) = 200/216 = 25/27 = 0.9259 = 92.59%
This shows us that 92.59% of tank B is 200pi cubic feet of water.
In other words, when all of tank A goes into tank B, we'll have tank B roughly 92.59% full.
This means the percentage of empty space (aka air) in tank B at this point is approximately 100% - 92.59% = 7.41%
Then finally, this value rounds to 7.4% when rounding to the nearest tenth of a percent.
Based on a $600 loan amount, rank the following companies from the lowest to highest annual percentage rate (APR)

Answers
The ranking from the lowest to highest APR for the given companies is A, B, D, C.
The correct option is b.
To rank the companies from the lowest to highest Annual Percentage Rate (APR) based on a $600 loan amount, we need to calculate the APR for each company. The formula to calculate APR is APR = (Fees / Loan Amount) * (365 / Terms of Loan).
Let's calculate the APR for each company:
For Company A:
APR_A = ($60 / $600) x (365 / 18) = 0.1 x 20.28 = 2.028%
For Company B:
APR_B = ($80 / $600) x (365 / 12) = 0.1333 x 30.42 = 4.054%
For Company C:
APR_C = ($90 / $600) x (365 / 10) = 0.15 x 36.5 = 5.475%
For Company D:
APR_D = ($110 / $600) x (365 / 14) = 0.1833 x 26.07 = 4.79%
Now, we can rank the companies from the lowest to highest APR:
Company A - APR: 2.028%
Company B - APR: 4.054%
Company D - APR: 4.79%
Company C - APR: 5.475%
To learn more about the percentage;
https://brainly.com/question/24159063
#SPJ1
Arrange the following from smallest to largest.

Answers
Please see attached picture.
Need help answering.

Answers
In the given graph, the x-intercepts are (2,0) and (6,0).
The axis of symmetry is the vertical line that passes through the vertex. Since the vertex is at (4,-2), the axis of symmetry is the line x = 4.
The interval on which the graph is increasing is (-∞,4), and the interval on which it is decreasing is (4,∞).
The sign of the leading coefficient is positive, since it is 1/2.
To find the equation of the quadratic function, we start by using the vertex form:
\(y = a(x - h)^2 + k\)
where (h, k) is the vertex. Plugging in the given vertex (4,-2), we get:
\(y = a(x - 4)^2 - 2\)
Next, we use the other two points to find two additional equations:
\(6 = a(8 - 4)^2 - 2 (plugging in (8,6))\\0 = a(2 - 4)^2 - 2 (plugging in (2,0))\)
Simplifying these equations, we get:
\(6 = 16a - 2\\8a = 4 -- > a = 1/2 \\0 = 4a - 2 \\4a = 2 -- > a = 1/2 \\\)
So the equation of the quadratic function is:
\(y = (1/2)(x - 4)^2 - 2\)
Now, we can answer the questions:
The y-intercept is the point where the graph intersects the y-axis. To find it, we set x = 0 in the equation:
\(y = (1/2)(0 - 4)^2 - 2 = 6\)
So the y-intercept is (0,6).
To find the x-intercepts, we set y = 0 in the equation:
\(0 = (1/2)(x - 4)^2 - 2\)
Simplifying, we get:
\((x - 4)^2 = 4\\ - 4 = \pm 2 \\= 2, 6\)
So the x-intercepts are (2,0) and (6,0).
The axis of symmetry is the vertical line that passes through the vertex. Since the vertex is at (4,-2), the axis of symmetry is the line x = 4.
The interval on which the graph is increasing is (-∞,4), and the interval on which it is decreasing is (4,∞).
The sign of the leading coefficient is positive, since it is 1/2.
To learn more about graphs from given link
https://brainly.com/question/21364844
#SPJ1

solve for u
\( \frac{u}{9} = \frac{8}{12} \)
simplify your answer as much as possible
Answers
Step 1: Cancel the common factor (4)
u = 2
—- —-
9 3
Step 2: multiply both sides by 9
9u 2 * 9
—- = ——-
9 3
Step 3: simplify
2 *9 = 18
18 ÷ 3 = 6
u = 6
HELP ASAP Which expression is equivalent to this polynomial expression?
(2x^2 - 3y^2)(4x^4 + 6x^2y^2 + 9y^4)
choices in picture
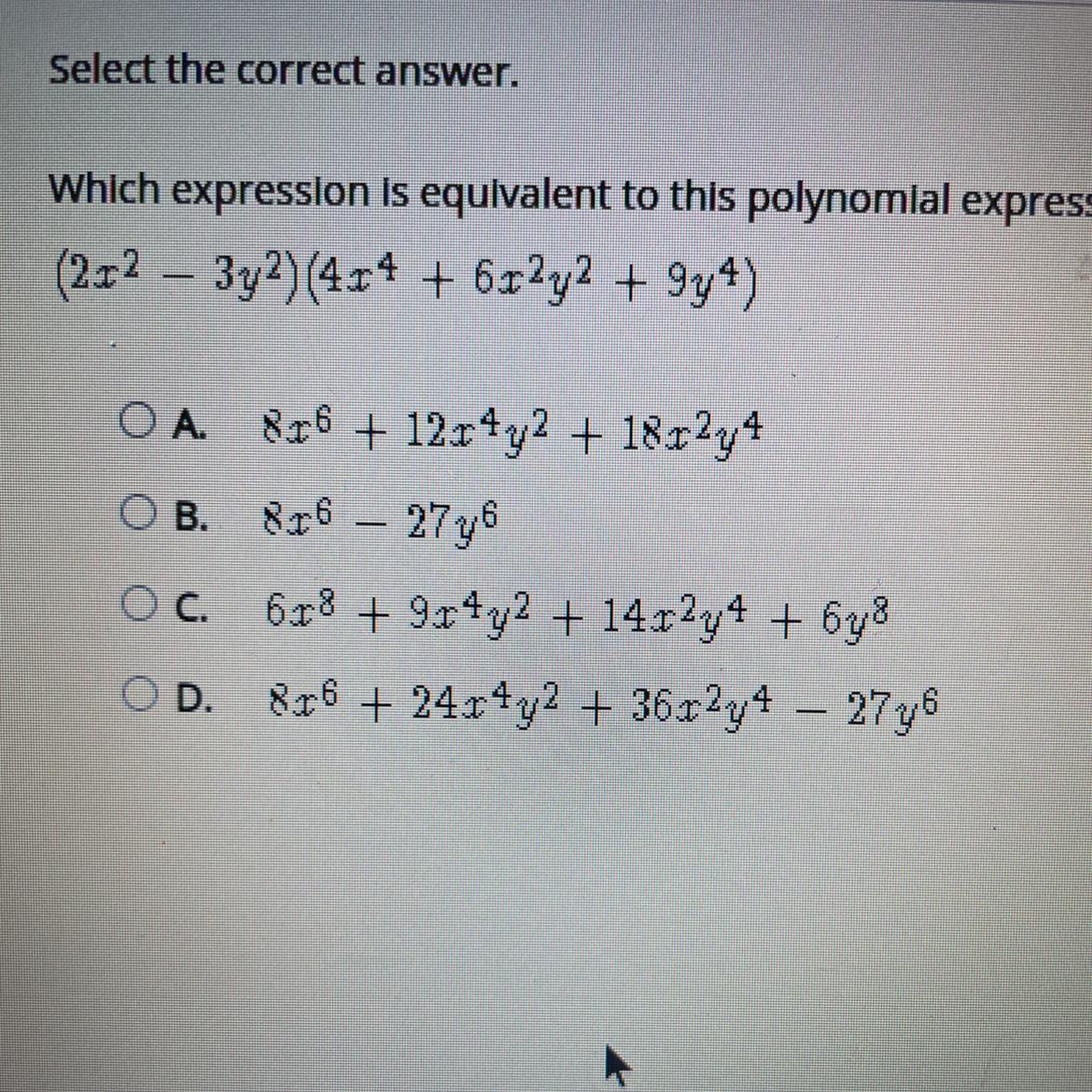
Answers
Answer:
B, if you have any questions how I did anything, or questions in general, let me know.
Step-by-step explanation:
First you want to make sure you understand distributing. Just using variables I will show how to districute a similar expression.
(a - b)(c + d - e)
There are several ways to think of it. you could treat (a-b) as one term and distribute it into c + d - e like this. pretend (a- b) = x
x(c + d - e) = cx + dx - ex = c(a-b) + d(a-b) - e(a-b)
Then just do a bit more distributing, then combine like terms.
You could instead make (c + d - e) a single term and distribute that into (a-b)
I prefer doing it all in one step, similar to FOIL-ing. Take the first term of one of the expression in parenthesis and distribute it, then move on to the second and so on.
so with (a - b)(c + d - e) I would start with a and distribute that into (c + d - e) and get ac + ad - ae then do the same to -b and get -bc - bd + be then you add the two parts together. ac + ad - ae + -bc - bd + be = ac + ad - ae -bc - bd + be. Then you would combine like terms. Let me know if you need help with that.
Anyway, now for your problem. Keep in mind you can use any of the methods.
(2x^2 - 3y^2)(4x^4 + 6x^2y^2 + 9y^4)
First distribute 2x^2 into (4x^4 + 6x^2y^2 + 9y^4)
8x^6 + 12x^4y^2 + 18x^2y^4
Next distribute -3y^2 into (4x^4 + 6x^2y^2 + 9y^4)
-12x^4y^2 - 18x^2y^4 - 27y^6
Now add the two together.
8x^6 + 12x^4y^2 + 18x^2y^4 + -12x^4y^2 - 18x^2y^4 - 27y^6 = 8x^6 + 12x^4y^2 + 18x^2y^4 - 12x^4y^2 - 18x^2y^4 - 27y^6
Finally combine like terms.
12x^4y^2 - 12x^4y^2 = 0
18x^2y^4 - 18x^2y^4 = 0
So that leaves us with 8x^6 - 27y^6
B is the only answer that works, none of the other 3 can be simplified or adjusted to make them equal what we need, so B is the only right answer.
If you have any questions though let me know.
If log₂(4x + 6) = 4, then x = ____
You may enter the exact value or round to 4 decimal places.

Answers
Answer: -1/2
Step-by-step explanation: To solve this problem, we can use the properties of logarithms to isolate the variable x on one side of the equation. The properties of logarithms tell us that the logarithm of a product is the sum of the logarithms of the factors, and that the logarithm of a power is the exponent times the logarithm of the base.
If log₂(4x + 6) = 4, we can rewrite the left side of the equation as follows: log₂(4x + 6) = log₂(2^4 * (2x + 3))
Then, using the property of logarithms that the logarithm of a product is the sum of the logarithms of the factors, we can simplify the equation as follows: log₂(4x + 6) = 4 + log₂(2x + 3)
Now, we can use the property of logarithms that the logarithm of a power is the exponent times the logarithm of the base to simplify the equation even further: log₂(4x + 6) = 4 + 1 * log₂(2x + 3)
Since the logarithm of a power is the exponent times the logarithm of the base, this means that the logarithm of a number is the logarithm of that number divided by the logarithm of the base. Therefore, we can divide both sides of the equation by log₂ to isolate the variable x on one side of the equation:
log₂(4x + 6) / log₂ = 4 + 1 * log₂(2x + 3) / log₂
(4x + 6) / 1 = 4 + (2x + 3) / 1
4x + 6 = 4 + 2x + 3
4x + 6 = 2x + 7
2x = -1
x = -1/2
Therefore, if log₂(4x + 6) = 4, then x = -1/2.
Help me ! Image below
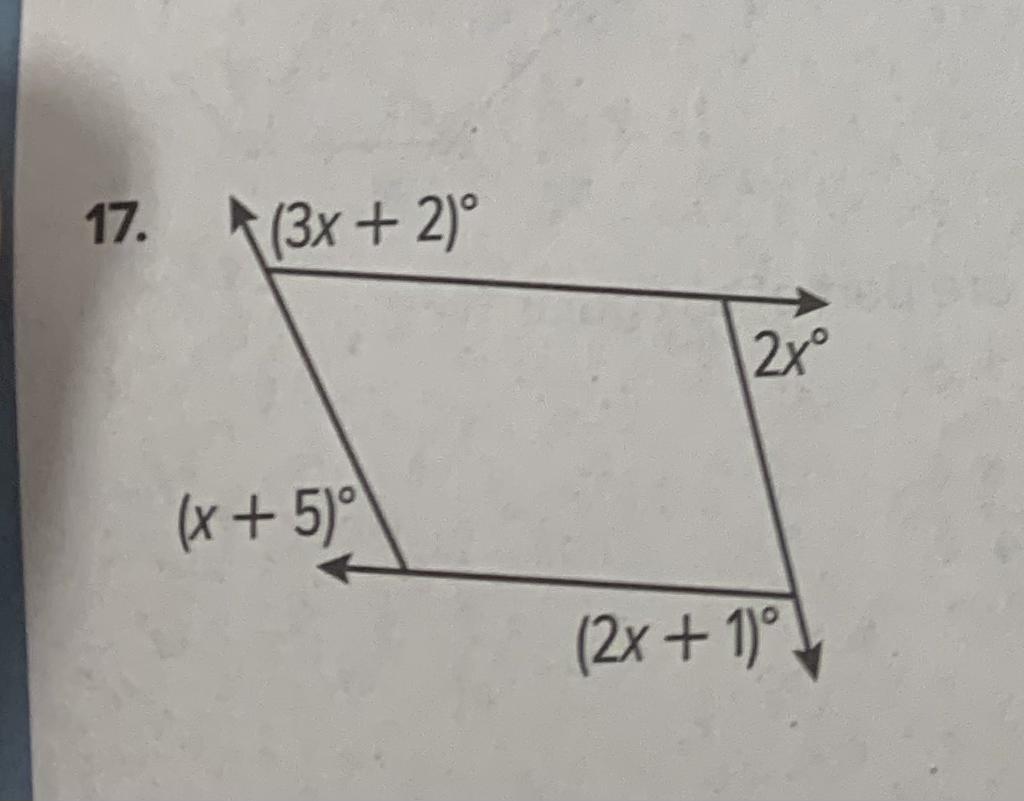
Answers
The sum of the exterior angles should be 360 degrees, using that, we will find that x = 44.
How to find the value of x?Remember that the sum of the interior angles of any quadrilateral must be 360°.
Then it is also the case for the correspondent exterrior angles.
So here we can write the linear equation:
(3x + 2) + 2x + (2x + 1) + (x + 5) = 360
And solve that for x.
3x + 2 + 2x + 2x + 1 + x + 5 = 360
8x + 8 = 360
8x = 360 - 8
8x = 352
x = 352/8 = 44
x = 44
That is the value of x.
Learn more about interior angles at:
https://brainly.com/question/24966296
#SPJ1
sarah the cheetah ran 100 meters at a speed of 16.8 meters per second. an olympian ran the 100 meter dash in 9.6 seconds . how much faster was sarah the cheetah's speed.
Answers
Answer:
3.6477seconds
Step-by-step explanation:
Sarah the cheetah ran the 100 meters in 5.9523s. Subtract 5.9523 from 9.6
2. A 2-pint bottle of olive oil costs $2.68. If
the unit price remains the same, how much will
gallons of olive oil cost?
Answers
Answer:
21.44 All you need to do is divide the 2.68 by 2 then multiply it by 16
A right triangle has leg lengths of 2.7 cm and 4.8 cm. What is the length of the hypotenuse? (Round to the nearest hundredth if necessary.)
Answers
Answer:
nñœñtîęñ do îñglęs...ææ
12 + 5 + 32 × 10 − 5 =
(12 + 5) + 32 × (10 − 5) =
Answers
Answer:
1. 332
2. 177
Step-by-step explanation:
Which best describes the solution set of the compound inequality below? 2 + x ≤ 3x – 6 ≤ 12 4 ≤ x ≤ 9 4 ≤ x ≤ 6 –2 ≤ x ≤ 2 –2 ≤ x ≤ 3
Answers
Answer:
Im sure you dont need this anymore but in case someone else does, im pretty sure the answer is B
Answer:
B is tha right answer
Step-by-step explanation:
Solve: 2m³-5m² - 7m = 0
Answers
Answer:
m = - 1 , m = 0 , m = \(\frac{7}{2}\)
Step-by-step explanation:
2m³ - 5m² - 7m = 0 ← factor out common factor m from each term
m(2m² - 5m - 7) = 0
factorise the quadratic 2m² - 5m - 7
consider the factors of the product of the coefficient of the m² term and the constant term which sum to give the coefficient of the m- term
product = 2 × - 7 = - 14 and sum = - 5
the factors are + 2 and - 7
use these factors to split the m- term
2m² + 2m - 7m - 7 ( factor the first/second and third/fourth terms )
2m(m + 1) - 7(m + 1) ← factor out (m + 1) from each term
(m + 1)(2m - 7)
then
2m³ - 5m² - 7m = 0
m(m + 1)(2m - 7) = 0 ← in factored form
equate each factor to zero and solve for m
m = 0
m + 1 = 0 ( subtract 1 from both sides )
m = - 1
2m - 7 = 0 ( add 7 to both sides )
2m = 7 ( divide both sides by 2 )
m = \(\frac{7}{2}\)
solutions are m = - 1 , m = 0 , m = \(\frac{7}{2}\)
find and interpret the probability that exactly 13 of those surveyed feel the state of morals is poor
Answers
Complete question is;
In a recent poll, the Gallup Organization found that 45% of adult Americans believe that the overall state of moral values in the United States is poor. Suppose a survey of a random sample of 25 adult Americans is conducted in which they are asked to disclose their feelings on the overall state of moral values in the United States. Find and interpret the probability that exactly 13 of those surveyed feel the state of morals is poor.
Answer:
P(X = 13) = 0.1236 or 12.36%
This means that in 100 trials, approximately 12 of the trials should have exactly 13 of those surveyed feel the state of morals is poor
Step-by-step explanation:
We are given;
Sample size; n = 25
Chance of success; p = 45% = 0.45
This question is a binomial probability distribution problem and the formula is;
P(X = x) = nCx × p^(x) × (1 - p)^(n - x)
probability that exactly 13 of those surveyed feel the state of morals is poor is;
P(X = 13) = (25C13) × 0.45^(13) × (1 - 0.45)^(25 - 13)
P(X = 13) = 5200300 × 0.00003102864 × 0.00076621787
P(X = 13) = 0.1236 or 12.36%
This means that in 100 trials, approximately 12 of the trials should have exactly 13 of those surveyed feel the state of morals is poor
What is the scale factor? please explain

Answers
Answer:
The scale factor is just the ratio like 3/15
little traingle/big triangle
Step-by-step explanation:
Harry and Sally both invest $2500 for their school tuition in 3 years. Harry chooses to invest his money at bank A at 2.5%/a compounded monthly while Sally chooses to invest her money at bank B at 2.75%/a compounded quarterly. How much money will Harry and Sally have in their bank account after 3 years? Who made the best investment? Explain your answer.
Answers
Answer:
Hola cómo te llamas Hola
What is the area of a triangle with vertices at (-4,1),(-7,5),and (0,1)
Answers
Answer:Find out the magnitude of each line segment
A=(-4, 1)
B= (-7, 5)
C=(0, 1)
Plot out the triangle to find out what the general shape of the triangle looks like since we need height.
A-B= √(-4+7)²+(1-5)²
=5
B-C=√(-7)²+(5-1)²
= √53
C-A=√(4)²+(1-1)²
=4
Find midpoint of B-C because line segment between A and B-C would be the height (according to the rough sketch previously drawn)
B-C= (x, y)= (x₁+x₂/2), (y₁-y₂/2)
(x, y)= (-7+0/2), (5+1/2)
(x, y)= -3.5, 3
Magnitude of A-BC:
√(-3.5+4)²(3-1)²
=√(0.5)²+4
Area=1/2(bh)
a=1/2(√53)(√(0.5)²+4 )
a= 7.5
Hope I helped you understand how you can derive the answer yourself :)
Step-by-step explanation:
which mixed number is equal to 18/8
2 6/9
2 5/8
2 1/4
1 2/8
Answers
Answer: 2 1/4
Step-by-step explanation:
p=(m+n)/-5 solve for n
Answers
n= -5p - m
dis is 20 characterrs now
Ian took out a $19,000 personal loan to pay for his home renovations. He will not make a payment for 5 years and there is a 15% interest rate. How much will be owed in 5 years with monthly compounding?
Round your answer to the nearest cent.
Do NOT round until your final answer.
Answers
The amount owed in 5 years with monthly compounding, considering a $19,000 personal loan with a 15% interest rate, will be $34,558.52.
1. Convert the interest rate to a decimal: 15% = 0.15.
2. Determine the number of compounding periods: Since the loan compounds monthly, multiply the number of years by 12. In this case, 5 years * 12 months/year = 60 months.
3. Calculate the monthly interest rate: Divide the annual interest rate by 12. In this case, 0.15 / 12 = 0.0125.
4. Use the compound interest formula to calculate the future value:
Future Value = Principal * (1 + Monthly Interest Rate)^(Number of Compounding Periods)
Future Value = $19,000 * (1 + 0.0\(125)^{(60\))
5. Evaluate the expression inside the parentheses: (1 + 0.0\(125)^{(60\)) ≈ 1.954503.
6. Multiply the principal by the evaluated expression: $19,000 * 1.954503 = $37,133.57 (unrounded).
7. Round the final answer to the nearest cent: $34,558.52.
Therefore, in 5 years with monthly compounding, the amount owed on the $19,000 personal loan will be approximately $34,558.52.
For more such questions on interest rate, click on:
https://brainly.com/question/25720319
#SPJ8
what is 6 over square root of 8x
Answers
Answer: 0.4714
Step-by-step explanation: square root of 8 is 2.8284 divided by 6 = 0.4714.
\( \frac{6}{ \sqrt{8x} } \\ \frac{ {6}^{2} }{ {( \sqrt{8x)} }^{2} } \\ \\ \frac{36}{8x} \\ \ \\ \frac{36 \div 4}{8x \div 4} \\ \\ \frac{9}{2x} \)
this is one of the ways to simplify it
you can divide 9 by 2 the answer will be 4.5x
Jamal's car averages 18.4 miles per gallon. How far can he expect to drive on 9.2 gallons of gas?
Answers
Answer:
169.28
Step-by-step explanation:
18.4x9.2=169.28
Grace invested $7,000 in an account paying an interest rate of 4.7% compounded
quarterly. Assuming no deposits or withdrawals are made, how long would it take, to
the nearest tenth of a year, for the value of the account to reach $11,870?
Answers
Answer:
11.3
Step-by-step explanation:
part a: the number of transistors per ic in 1972 seems to be about 4,000 (a rough estimate by eye). using this estimate and moore's law, what would you predict the number of transistors per ic to be 20 years later, in 1992? prediction
Answers
Using Moore's Law, which states that the number of transistors on a chip doubles approximately every two years, the estimated number of transistors per IC in 1992 would be 64,000.
The law claims that we can expect the speed and capability of our computers to increase every two years because of this, yet we will pay less for them. In more simple terms, the observation by Gordon Moore in 1965 that the number of transistors in a dense integrated circuit (IC) doubles roughly every two years is known as Moore's law.
This is calculated by doubling the estimate of 4,000 transistors every two years for a total of 8 doublings (16 years).
To know more about Law here
https://brainly.com/question/6590381
#SPJ4
