Answers
Answer:
l1 and l2 are not parallel
Step-by-step explanation:
113 is not equal to 115.
For l1 to be parallel to l2, corresponding angles must be equal and 113 and 115 are corresponding angles.
I1 is not || I2
hope this helps u
pls mark me as brainliest
Related Questions
Determine the sum of the series
∑[infinity]n=15n(n+2)
if possible. (if the series diverges, enter 'infinity, "-infinity" or "dne' as appropriate.)
Answers
The sum of the series ∑[infinity]n=15n(n+2) is 'dne' (does not exist) as the series diverges.
To determine the sum of the series, we first need to check if the series converges or diverges.
The series is given as:
∑[infinity]n=15n(n+2)
Step 1: Identify the type of series
This is an infinite series with terms involving a polynomial in n.
Step 2: Apply the Ratio Test
The Ratio Test is used to determine the convergence or divergence of a series. Let's take the ratio of consecutive terms:
lim (n→∞) \((|a_(n+1) / a_n|)\)
where, \((|a_(n+1) / a_n|)\)
\(a_(n+1) = (n+1)((n+1)+2) = (n+1)(n+3)\)
So, we have:
lim (n→∞) (|((n+1)(n+3))/(n(n+2))|)
Step 3: Simplify the limit
To simplify the limit, divide both the numerator and the denominator by the highest power of n,
which is \(n^2:\)
lim (n→∞) (|((1+(1/n))(1+(3/n)))/((1)(1+(2/n)))|)
Step 4: Calculate the limit
As n approaches infinity, the terms with 1/n will approach 0:
lim (n→∞) (|(1)(1+0)/(1+0)|) = 1
Step 5: Interpret the result
Since the limit is 1, the Ratio Test is inconclusive, and we cannot determine if the series converges or diverges based on this test alone.
However, since the series is an infinite series with terms involving a polynomial in n, it will diverge.
This is because the terms do not approach 0 as n approaches infinity.
For similar question on series.
https://brainly.com/question/30087275
#SPJ11
Find the height of the tower using the information given in the illustration.

Answers
using SOH CAH TOA
Tan 85.144 =h/130
h=tan 85.144*130
h=1530.19 fr

Find the principal:
Interest Rate: 16%
Interest: $18
Time: 3 months
Answers
$450 if you need the process ask me will give it to you
A bag contains 3 green marbles and 5 white marbles. Paul picks a marble at random from the
bag and does not put it back in the bag. He then picks another marble from the bag.
a. Construct a probability tree of the problem.
Answers
A probability tree is a visual representation of the possible outcomes of an event or series of events. In this case, the event takes a marble out of the bag.
How to create the tree?The first step in building a probability tree is to create a starting point that represents the first state of the problem. In this case, the starting point is a bag containing 3 green marbles and 5 white marbles.
The next step is to branch from the starting point and show the possible results of the first event. This includes taking out the marble out of the bag. The probability of getting a green marble is 3/8 and the probability of getting a white marble is 5/8.
After the first event, the issue status changes. In this case, the bag contains 2 green marbles and 4 white marbles.
The next step is to branch out from the state after the first event and show the possible outcomes of his second event involving pulling another marble out of his pocket. The probability of getting a green marble is 2/6 and the probability of getting a white marble is 4/6. The final step is to label the endpoints of the tree with the possible outcomes of the problem and the probabilities of each outcome.
The probability tree starts with an sack of 3 green marbles and 5 white marbles, as shown in the design showing the possible outcomes of selecting a marble, the new state of the sack after each selection, and the probability of each outcome
To know more about probability tree visit:
https://brainly.com/question/28916734
#SPJ1
find the domain and range of the function. Use a graphing utility to verify your results. (Enter your answer using interval notation.)
f(x) = ?x2 ? 6x + 7
Answers
The domain is [0,100].[0,100]. The range is [0,1500] [0,1500]
(a) To find the cost of making 25 items substitute
x=25 in the equation
=10+500(25)
=10(25)+500(25)=750
c(x)=10x+500
c(25)=10(25)+500
c(25)=750
the cost of making 25 items is
$750
(b)
Since the maximum cost allowed is
$1500
10+500≤1500
10x+500≤1500
To solve this inequality
First, subtract 500 from both sides
10≤1000
10x≤1000
Divide both sides by 10
≤100x≤100
This means you can make at most 100 items.
The domain is
[0,100].[0,100].
The range is
[0,1500] [0,1500].
Know more about the domain
https://brainly.com/question/2264373
#SPJ4

Please help me please!!
(Picture above)

Answers
Answer:
1) D
2) C
3) B
4) A
Step-by-step explanation:
type them into desmos online calculator to see the lines
What is the discounted price for a watch that is regularly $58.00 and 30% off?
Answers
Answer:
$40.60
Step-by-step explanation:
Please help me with 10

Answers
Answer:
yes the answer is he does make sense
You intend to estimate a population proportion with a confidence interval. The data suggests that the normal distribution is a reasonable approximation for the binomial distribution in this case. While it is an uncommon confidence level, find the critical value that corresponds to a confidence level of 97.1%.
Answers
Answer:
The critical value that corresponds to a confidence level of 97.1% is \(Z = 2.18\).
Step-by-step explanation:
In a sample with a number n of people surveyed with a probability of a success of \(\pi\), and a confidence level of \(1-\alpha\), we have the following confidence interval of proportions.
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which
z is the z-score that has a p-value of \(1 - \frac{\alpha}{2}\).
97.1% confidence level
So \(\alpha = 0.029\), z is the value of Z that has a p-value of \(1 - \frac{0.029}{2} = 0.9855\), so \(Z = 2.18\).
The critical value that corresponds to a confidence level of 97.1% is \(Z = 2.18\).
Please help questions is down below.
Please answer all!
No bots pls!!!!!! Ill give brain thing


Answers
Question 2: 19/24 (not completely sure)
Question 3: 11/21
-10
A'
9
T
&
-2
В'
N
T
OF
23
-5
-10
2
3
B
Determine the direction and degree of rotation used to create the image.
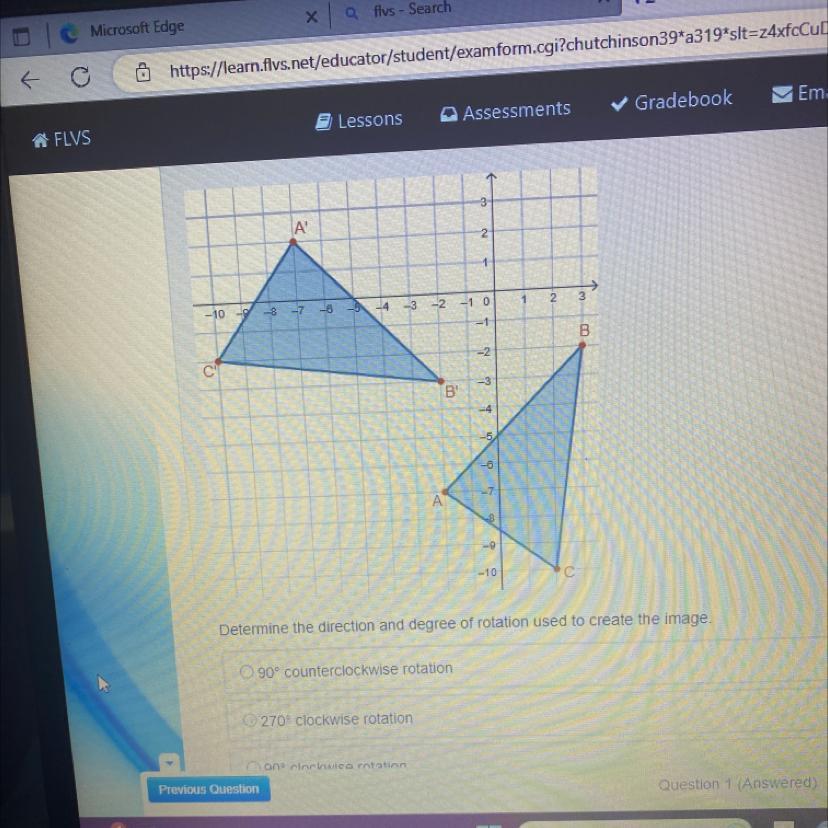
Answers
The direction and degree of rotation used to create the image include the following: C. 90° clockwise rotation.
What is a rotation?In Mathematics and Geometry, a rotation is a type of transformation that moves every point of the object through a number of degrees around a given point, which can either be clockwise or counterclockwise (anticlockwise) direction.
By applying either a rotation of 90° clockwise or a rotation of 270° counterclockwise to the coordinate of triangle ABC, the coordinate of its image (triangle A′B′C′);
(x, y) → (y, -x)
Point A = (-2, -7) → Point A′ (-7, 2)
Point B = (3, -2) → Point B′ (-2, -3)
Point C = (2, -10) → Point C′ (-10, -2)
Read more on rotation here: brainly.com/question/28854313
#SPJ1
Complete Question:
Determine the direction and degree of rotation used to create the image.
90° counterclockwise rotation
270° clockwise rotation
90° clockwise rotation
180° clockwise rotation

2 x + 3 = x − 4 solve for x
Please anyone?
Answers
Answer:
x=-7
Step-by-step explanation:
\(2x - x = - 4 - 3\)
\(x = - 7\)
i think this is the answer
Answer:
x = -7
Step-by-step explanation:
subtract 3 from both sides and subtract x from both sides
x = -7
In ΔQRS, m∠R = 57°, q = 9, and s = 5. Find the area of ΔQRS.
Answers
The area of ΔQRS is 26.10 square units.
What is triangle?
A triangle is a closed, two-dimensional geometric shape with three straight sides and three angles.
To find the area of \($\triangle QRS$\), we can use the formula:
\($Area = \frac{1}{2} \times base \times height$\)
where the base and height are the length of two sides of the triangle that are perpendicular to each other. We can find these sides using trigonometry.
First, we need to find the length of side \($QR$\). We can use the Law of Cosines:
\($QR^2 = QS^2 + RS^2 - 2(QS)(RS)\cos(R)$\)
where \($R$\) is the angle at vertex \($R$\). Substituting the given values, we get:
\($QR^2 = 9^2 + 5^2 - 2(9)(5)\cos(57^\circ)$\)
\($QR \approx 8.02$\)
Next, we need to find the height of the triangle, which is the perpendicular distance from vertex \($R$\) to side \($QS$\). We can use the sine function:
\($\sin(R) = \frac{opposite}{hypotenuse}$\)
\($\sin(57^\circ) = \frac{height}{8.02}$\)
\($height \approx 6.51$\)
Now we can find the area of the triangle:
\($Area = \frac{1}{2} \times QR \times height$\)
\($Area = \frac{1}{2} \times 8.02 \times 6.51$\)
\($Area \approx 26.10$\) square units
Therefore, the area of \($\triangle QRS$\) is approximately \($26.10$\) square units.
To learn more about triangle visit:
https://brainly.com/question/1058720
#SPJ1
82°
118°
95°
X°
Image not to scale
Calculate the missing angle x.

Answers
Answer:
x = 65
Step-by-step explanation:
the sum of the interior angles of a quadrilateral = 360°
sum the angles and equate to 360
x + 95 + 118 + 82 = 360
x + 295 = 360 ( subtract 295 from both sides )
x = 65
The surface are of the right triangular prism is 120ft what is the volume of the prism? Show your work
Please help soon I need it now!
I give 30 brainly

Answers
The volume of the prism is 48.75cm³
What is volume of a prism?Volume is defined as the space occupied within the boundaries of an object in three-dimensional space.
A prism is a solid shape that is bound on all its sides by plane faces.
The volume of the prism is expressed as;
V = base area × height
base area = 1/2 bh
area = 1/2 × 6 × 5/2
= 30/4
= 7.5 cm²
Height of the prism = 13/2 = 6.5 cm
Therefore the volume
= 7.5 × 6.5
= 48.75 cm³
learn more about volume of prism from
https://brainly.com/question/23963432
#SPJ1
Let f:R" + R be a convex function. Show that (i) and (ii) are equivalent definitions for m-strong convexity:(i) f(x) – m. || 2 || 2 is convex.(ii) f (4x + (1 - 1)y) = \f (x) + (1 - 1)f (y) – m (1 – 1)||2 – y||2 for all x, y ER" and [0, 1]. 2If in addition f is differentiable then show (i) and (ii) are equivalent to (iii): т (iii) f(y) > f(x) + f(x)?(y – x) + m || 2 – y||
Answers
For f: R" + R be a convex function (i) and (ii) are equivalent definitions for m-strong convexity because m[||px + (1-p)y||².
Let x, y ∈ \(R^n\) and let 0 < p < 1. Then we have:
||px + (1-p)y|| ≤ ||px|| + ||(1-p)y|| [triangle inequality]
= p||x|| + (1-p)||y|| [since ||cx|| = |c| ||x|| for any scalar c]
Now, since f is convex, we have:
f(px + (1-p)y) ≤ pf(x) + (1-p)f(y)
Using the inequality above, we can substitute the right-hand side of this inequality as follows:
f(px + (1-p)y) ≤ pf(x) + (1-p)f(y)
f(px + (1-p)y) - pf(x) ≤ (1-p)f(y)
f(px + (1-p)y) - pf(x) + p(f(x) - f(y)) ≤ 0
Define h(p) = f(px + (1-p)y) - pf(x) - p(f(x) - f(y))
Then we have h(0) = f(y) - f(x) ≥ 0 and h(1) = f(x) - f(x) = 0.
Moreover, h is differentiable, since f is differentiable, and we have:
h'(p) = ∇\(f(px + (1-p)y)^T\) (x - y)
= \((x - y)^T\) ∇f(px + (1-p)y)
= \((x - y)^T\) [f(px + (1-p)y) - f(x)]
= \((x - y)^T\) [f(px + (1-p)y) - f(px) + f(px) - f(x)]
= \((x - y)^T\) [f(px + (1-p)y) - f(px)] + \((y - x)^T\) [f(px) - f(x)]
= p\((x - y)^T\) ∇f(px) + (1-p)\((y - x)^T\) ∇f(py)
= p\((x - y)^T\) ∇² f(px)(x - y) + (1-p)\((y - x)^T\) ∇² f(py)(y - x)
where the last equality follows from the mean value theorem for differentiation.
Since f is m-strongly convex, we have ∇² f(x) ≥ mI for all x ∈ \(R^n\), where I is the n x n identity matrix. Therefore,
h'(p) ≥ \(p(x - y)^T\) mI(x - y) + (1-p)\((y - x)^T\) mI(y - x)
= m||px + (1-p)y - x||² - m||px - x||² - m||(1-p)y - x||²
= m||px + (1-p)y - x||² - mp²||x||² - m(1-p)²||y||²
= m[p²||x||² - 2p||x||² + ||px + (1-p)y||²] + m[(1-p)²||y||² - 2(1-p)||y||² + ||px + (1-p)y||²]
= m[||px + (1-p)y||² - 2p||x||² - 2(1-p)||y||²]
= m[||px + (1-p)y||² - p²||x||² - (1-p)²||y||²]
= m[||px + (1-p)y||²]
Learn more about the convex function at
https://brainly.com/question/30340321
#SPJ4
Select the correct answer.
Which sentence correctly describes a data set that follows a normal distribution with a standard deviation of 4 and a mean of 14?
68% of the data points lie between 10 and 14.
68% of the data points lie between 8 and 12.
68% of the data points lie between 10 and 18.
68% of the data points lie between 10 and 16.
Answers
Answer:
68% of the data points lie between 10 and 18.
Step-by-step explanation:
one standard deviation to left of mean = 14 - 4 =10
one standard deviation to right of mean = 14 + 4 = 18
68% of data is in this region.
so the answer is 68% of the data points lie between 10 and 18.
A biker traveled 2/5 of the road on the first day, then traveled 5 kilometers less on the next day, which is equal to 3/8 of the road. How much more does he need to travel? (distance)
Answers
The biker needs to travel 45 km more to complete his journey.
Given that, a biker traveled 2/5 of the road on the first day, then traveled 5 kilometers less on the next day, which is equal to 3/8 of the road, we need to find how much he need to cover more,
Let the total distance of the road be x,
So,
2x/5 - 5 = 3x/8
2x/5 - 3x/8 = 5
Solving for x,
Multiply by 40 to both sides,
16x-15x = 200
x = 200
Therefore, the total distance of the road is 200 km.
Since, he travelled =
200 (2/5) = 80 km + 200 (3/8) = 75 km = 155 km
Therefore, he needs to travel 200-155 = 45 km more.
Hence, the biker needs to travel 45 km more to complete his journey.
Learn more about equations, click;
https://brainly.com/question/29657983
#SPJ1
A line with a slope of 1 passes through the point (5, 3). What is its equation in slope "-intercept" form?
Answers
Answer: y=x−2 y = x − 2
Step-by-step explanation:
how do i solve intervals
Answers
What’s the answer? Will give brainliest

Answers
Answer:
Step-by-step explanation:
3
What is the slope of the line?
y+3 = -4(2 + 7)

Answers
Answer:-4
Step-by-step explanation:
The body temperatures of a group of healthy adults have a bell-shaped distribution with a mean of 98.27°F and a standard
deviation of 0.54°F. Using the empirical rule, find each approximate percentage below.
a. What is the approximate percentage of healthy adults with body temperatures within 1 standard deviation of the mean, or
between 97.73 °F and 98.81°F?
Answers
Answer: follow this you'll be able to solve it
Step-by-step explanation: mean = 98.11F
standard deviation = 0.56F
99.79 – 98.11 = 1.68 = 3 standard deviations
96.43 – 98.11 = –1.68 = –3 standard deviations
96.43F and 99.79F are 3 standard deviations from the mean 98.11F.
By the empirical rule we know that 99.7% of the data lies within 3 standard deviation of the mean.
Approximately 68% of healthy adults in this group have body temperatures within 1 standard of the mean, or between 97.55F and 98.67F.
2. What is the best form to use in order to determine the X- AND y-intercepts?
Answers
Answer:
Step-by-step explanation:
To determine the x-intercept, we set y equal to zero and solve for x. Similarly, to determine the y-intercept, we set x equal to zero and solve for y. For example, lets find the intercepts of the equation y = 3 x − 1 \displaystyle y=3x - 1 y=3x−1. To find the x-intercept, set y = 0 \displaystyle y=0 y=0.
1.To determine the x-intercept, we set y equal to zero and solve for x. Similarly, to determine the y-intercept, we set x equal to zero and solve for y.
2.To find the x-intercept, set y = 0 \displaystyle y=0 y=0.
3.To find the y-intercept, set x = 0 \displaystyle x=0 x=0.
hellpp fast please a

Answers
Answer:
C. 3x+30
Step-by-step explanation:
5(2x+6)-7x can be rewritten as
10x+30-7x which can be simplified as
3x+30
60 cars to 20 cars indenify percent of change
Answers
Answer: -66.67%, but if the answer is supposed to positive then the answer is 66.67%.
* Hopefully this helps:)
Which symbol correctly relates 23 ? 16 check all that apply

Answers
Answer:
C and E
Step-by-step explanation:
23 > 16 and \(23\geq 16\) are both true statements since the quantity of 23 is greater than that of 16.
Which of the following coordinates exists on the line y = 2x + 4?
A. (2, 4)
B. (1, 5)
C. (-3, -2)
D. (-1, 3)
Answers
identify the relationship that does not represent a direct variation

Answers
Remember that
In a direct variation
we have an equation of the form
y=kx
where
k is the constant of proportionality o slope of the linear equation
so
Verify each table
N 1
Find out the value of k
k=y/x
(5,1) ----> k=1/5
(7,2) ----> k=2/7
the values of k are not equal
that means
not represent a direct variation
N2
(6,3) -----> k=3/6=1/2
(12,6) -----> k=6/12=1/2
(18,9) ----> k=9/18=1/2
the values of k are the same
so
represent a direct variation
N 3
(2,10) -----> k=10/2=5
(4,20) ----> k=20/4=5
(8,40) ----> k=40/8=5
the values of k are the same
so
represent a direct variation
N 4
(4,2) ----> k=2/4=1/2
(8,4) -----> k=4/8=1/2
(12,6) ----> k=6/12=1/2
the values of k are the same
so
represent a direct variation
therefore
the first table does not represent a direct variationA basketball player makes 40% of his shots from the free throw line. Suppose that each of his shots can be considered independent and that he throws 3 shots. Let x = the number of shots that he makes. What is the sample space for x?.
Answers
The probability of throwing 3 shots is 100% and the sample space is set of all possible real number.
Probability is the measure of the likelihood that a given event will occur. In this case, the event is a basketball player making a shot from the free throw line.
Since the player has a 40% success rate, we can calculate the probability of him making x number of shots, where x is the number of shots that he throws.
Since the shots are independent of each other, the sample space for x is the set of all possible numbers of shots that he can make, from 0 to the total number of shots (3 in this case).
Therefore, the sample space for x is {0, 1, 2, 3}, which means that the player has a 0% probability of making 0 shots, a 40% probability of making 1 shot, an 80% probability of making 2 shots, and a 100% probability of making all 3 shots
To know more about probability here.
https://brainly.com/question/11234923
#SPJ4
