Given the speeds of each runner below, determine who runs the fastest.
\text{Frank runs 9 feet per second.}
Frank runs 9 feet per second.
\text{Tony runs 299 feet in 34 seconds.}
Tony runs 299 feet in 34 seconds.
\text{Zach runs 1 mile in 396 seconds.}
Zach runs 1 mile in 396 seconds.
\text{Will runs 675 feet in 1 minute.}
Will runs 675 feet in 1 minute.
Answers
Tony 8.79feet per second
Zach 13.34feet per second
Will 11.25feet per second
Tony runs fastest
Zach runs with 14.31 feet per second speed and faster than other runners.
What is Speed?Speed is measured as the ratio of distance to the time in which the distance was covered
Given that Frank runs 9 feet per second.
Speed=Distance /time
=9 feet/ 1 second
=9 feet per second.
Tony runs 299 feet in 34 seconds
Speed=299/34
=8.794 feet per second.
Zach runs 1 mile in 396 seconds.
We know that 1 mile =5280 feet
Speed=5280/369
=14.31 feet per second.
Will runs 675 feet in 1 minute
1 minute is 60 seconds
Speed=675/60
=11.25 feet per second.
Hence, Zach runs with 14.31 feet per second speed and faster than other runners.
To learn more on Speed click:
https://brainly.com/question/28224010
#SPJ2
Related Questions
A randomized study compared two drugs that
are designed to lower a person's triglyceride
level. It was found that over a 1-year period,
those receiving Drug A decreased their
triglyceride level by a mean of 69. Those
receiving Drug B decreased their triglyceride
level by a mean of 45.
To determine whether the results are significant,
the data are rerandomized and the difference of
the means is shown in the dot plot.
What is the best conclusion to make based on
the data?
Answers
Answer:b
Step-by-step explanation:
2 3/8 ÷ 1 1/4
Steps
19/8 x 4/5
= 19/10
= 1 9/10
So the answer to this is B.
What is the slope of segment AB? Round to the nearest tenth

Answers
answer:
3/8 is the slope, also stated as .4 (from 3.75)
the segment length is 8.5 (using the pythagorean theorem)
The sum of three consecutive even integers is 42. What is the product of the smallest and largest
integer?
Answers
Step-by-step explanation:
Hope this help po, thank you.

I don't under stand what is wrong.

Answers
Answer:
In the first step, there is an issue when distributing the -3 to the terms inside of the parentheses. When multiplying the -3 to the -5, you would get an answer of +15, not -15.
The full correct process is:
(4m + 9) - 3(2m - 5) = 4m + 9 - 6m + 15
= 4m - 6m + 9 + 15
= -2m + 24
What is the approximate value for tan C?
Answers
You put C's value into your calculator, then push the TAN button to get your answer. Normally you round to 4 digits past zero. You didn't include any values so I can't give you an exact answer. Hope that helps!
Answer:
Step-by-step explanation:
To determine the approximate value of tan C, we need to know the value of angle C. If we have that information, we can use a calculator or a trigonometric table to find the value of the tangent function for that angle.
If angle C is not given, we cannot determine the value of tan C.
Find the angle between the following two vectors.
< 8, 3 > and < 4, −3 >
Answers
The angle between the two vectors < 8, 3 > and < 4, −3 > is 57.43°
How to determine the angle between the following two vectors?Given: vectors < 8, 3 > and < 4, −3 >
To find the angle between two vectors, we can use the dot product method:
First, you will compute the dot product and magnitudes of both vectors. Thus,
Let a = < 8, 3 > and b = < 4, −3 >
a · b = <8, 3> ·<4, -3> = 8(4) + (3)(-3) = 32-9 = 23
|a| = √(8² + 3²) = √(64+9) = √73
|b| = √(4² + (-3)²) = √(16 + 9) = √25 = 5
By using the angle between two vectors formula using dot product,
θ = cos⁻¹ [ (a · b) / (|a| |b|) ]
θ = cos⁻¹ (23 / √73 · 5)
θ = cos⁻¹ (23/42.72) = 57.43°
Therefore, the angle between the following two vectors is 57.43°
Learn more about vectors on:
https://brainly.com/question/25730276
#SPJ1
.Problem 3. (30 marks] 3-1. Determine the error term for the formula [5] answer f'(a) ~ 2.14f(a + h) – 3f(x) – f(x + 2h)] 2h ately 3-2. Use the above formula to approximate f'(1.8) with f(x) In x using h= 0.1, 0.01 and 0.001. Display your results in a table and then show that the order of accuracy obtained from your results is in agreement with the theory in question 3-1. (10) 3-3. Establish the error term for the rule: [15] f"(a) ~h( x) = [3f(x + h) - 10f(x) + 12f(x - h) - 6f(x - 2h) + f(x - 3h)] 1 2h3 -
Answers
The error term for the given rule is: [f''''(x) / 5] * h²[f''''(x) / 5] * h² is the error term for the given rule.
Error term = [f''(x) / 12] * h², therefore, the error term for the given formula is:
f''(x) = [f'(x + h) - f'(x)] / h[f'(a)
≈ 2.14f(a + h) – 3f(x) – f(x + 2h) / 2h]
Then we have to calculate the second derivative of f(x) to calculate the error term: f''(x) = [f'(x + h) - f'(x)] / hf''(x)
= [f(x + 2h) - 2f(x + h) + 2f(x - h) - f(x - 2h)] / (2h)²
So, the error term is: f''(x) / 12 = [f(x + 2h) - 2f(x + h) + 2f(x - h) - f(x - 2h)] / 12h² f'(a) ≈ 2.14f(a + h) – 3f(x) – f(x + 2h) / 2h has an error term of [f(x + 2h) - 2f(x + h) + 2f(x - h) - f(x - 2h)] / 12h².3-2.
Use the above formula to approximate f'(1.8) with f(x) In x using h= 0.1, 0.01 and 0.001.
To know more about error visit:-
https://brainly.com/question/22248350
#SPJ11
can you guys please help me?

Answers
Frequency means how often a number or something appears.
so,
2
4
3
5
5 x 1/7
The question

Answers
Answer:
5/7 or 0.71 is the answer
Find the ratios of the six trigonometric functions for angle 0 . No decimals!

Answers
Answer: ooooooof
Step-by-step explanation:
Demand history for the past three years is shown below, along with the seasonal indices for each quarter.
Year Quarter Demand Seasonal Index
Year 1 Q1 319 0.762
Q2 344 0.836
Q3 523 1.309
Q4 435 1.103
Year 2 Q1 327 0.762
Q2 341 0.836
Q3 537 1.309
Q4 506 1.103
Year 3 Q1 307 0.762
Q2 349 0.836
Q3 577 1.309
Q4 438 1.103
Use exponential smoothing with alpha (α) = 0.35 and an initial forecast of 417 along with seasonality to calculate the Year 4, Q1 forecast.
Answers
The Year 4, Q1 forecast using exponential smoothing with α = 0.35 and an initial forecast of 417, along with seasonality, is 335.88.
Exponential smoothing is a forecasting technique that takes into account both the historical demand and the trend of the data. It is calculated using the formula:
Forecast = α * (Demand / Seasonal Index) + (1 - α) * Previous Forecast
Initial forecast (Previous Forecast) = 417
α (Smoothing parameter) = 0.35
Demand for Year 4, Q1 = 307
Seasonal Index for Q1 = 0.762
Using the formula, we can calculate the Year 4, Q1 forecast:
Forecast = 0.35 * (307 / 0.762) + (1 - 0.35) * 417
= 335.88
Therefore, the Year 4, Q1 forecast using exponential smoothing with α = 0.35 and an initial forecast of 417, along with seasonality, is 335.88.
The forecasted demand for Year 4, Q1 using exponential smoothing is 335.88.
To know more about exponential smoothing , visit
https://brainly.com/question/15061467
#SPJ11
help im gaveing points:)

Answers
Answer:
8
Step-by-step explanation:
for the following initial value problem, compute the first two approximations u1 and u2 given by Euler’s method using the given time stepy’(t)=t+y; y(0)=5; triangle t=0.3u1=u2=
Answers
Using Euler's method with a time step of 0.3, the first two approximations for the solution to the initial value problem y'(t) = t + y, y(0) = 5 are u1 = 6.5 and u2 = 8.035.
Using Euler's method, we can approximate the solution to the initial value problem y'(t) = t + y, y(0) = 5 with a time step of Δt = 0.3 as follows:
At t = 0, y = 5
Using the formula: y1 = y0 + f(y0,t0)Δt, where f(y,t) = t + y
y1 = 5 + (0 + 5)0.3 = 6.5
Using the formula again with y1 and t1 = Δt:
y2 = 6.5 + (0.3 + 6.5)0.3 = 8.035
Thus, the first two approximations u1 and u2 are 6.5 and 8.035, respectively.
To learn more about Euler's method click here: brainly.com/question/30699690
#SPJ11
I need help with my last question

Answers
Suppose () = 1/8 for 0 ≤ ≤ 4 for x being a continuous random variable Is () a probability density function? Prove or disprove.
Answers
Answer:
The expected value of x ; E(x) = 1
Step-by-step explanation:
F(x) = 1/8 for 0 ≤ x ≤ 4
To prove that it is a probability density function we will find E(x )
attached below is the required prove
It is proven that F(x) = 1/8 for 0 ≤ x ≤ 4 is probability density function
The expected value of X = 1
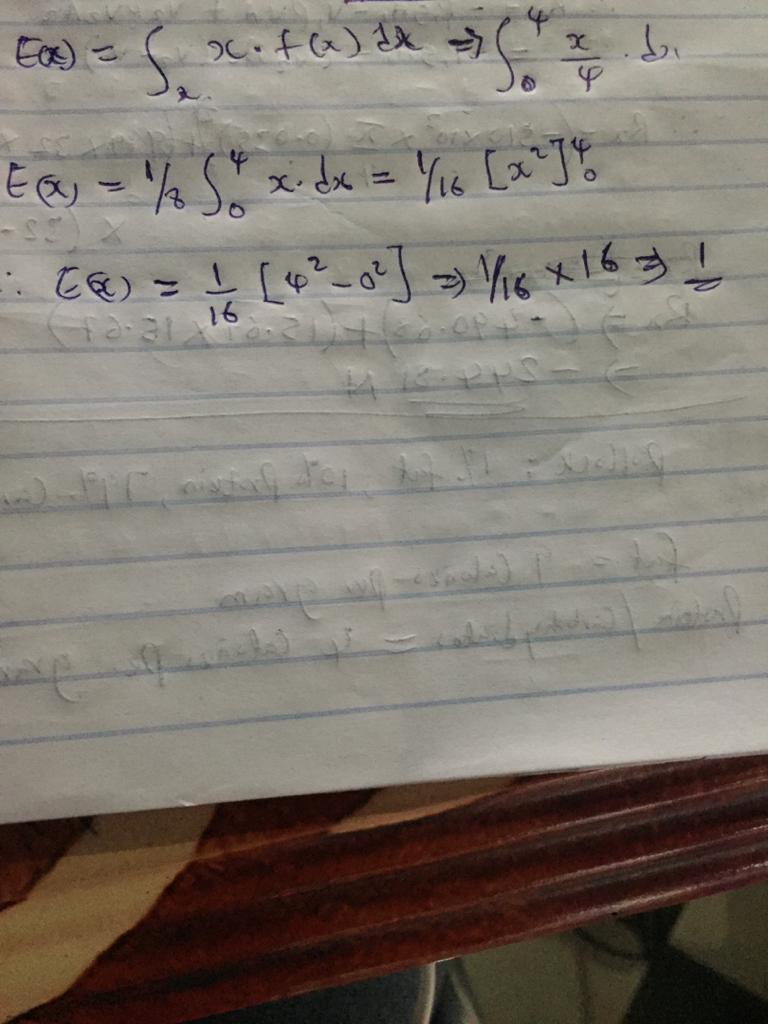
Put this in least to greatest

Answers
Answer:
1. Square root of 8 over 2 (1.41)
2. 2
3. Square root of 7 (2.65)
the area of a parallelogram is 48cm².if the two adjacent sides are 8cm and 6cm, find the length of its diagonal .
Answers
Answer:
10cm
Step-by-step explanation:
Assuming the shape is a rectangle since it's already stated that it's a parallelogram, and the area is stated, we can use the Pythagorean theorem to find the length
\(a^{2} +b^2=c^2\), where c will be the length
isolate c
\(c^2=a^2+b^2\)
\(c=\sqrt{a^2+b^2}\)
substitute for a and b
\(c=\sqrt{8^2+6^2}\)
\(c=\sqrt{64+36}\)
\(c=\sqrt{100}\)
\(c=10\)
explain which properties of equality you used when solving the equation from part a to determine the mystery weight.
Answers
To solve the equation in part a and determine the mystery weight, we used the following properties of equality:
Addition property: This property states that if we add the same number to both sides of an equation, the equality is preserved. In this case, we added 23 grams to both sides of the equation to isolate the variable.
Subtraction property: This property states that if we subtract the same number from both sides of an equation, the equality is preserved. In this case, we subtracted 8 grams from both sides of the equation to isolate the variable.
Multiplication property: This property states that if we multiply both sides of an equation by the same number, the equality is preserved. In this case, we multiplied both sides of the equation by 3 to isolate the variable.
Division property: This property states that if we divide both sides of an equation by the same number (excluding 0), the equality is preserved. In this case, we divided both sides of the equation by 2 to isolate the variable.
By using these properties of equality, we were able to manipulate the equation and isolate the variable to determine the mystery weight.
To learn more about equations from given link
https://brainly.com/question/22688504
#SPJ1
The television show NBC Sunday Night Football broadcast a game between the Colts and Patriots received a share of 22, meaning that among the TV sets in use, 22% were tuned to the game (based on Nielson data). An advertiser wants to obtain a second opinion by conducting its own survey, and a pilot survey begins with 33 households having TV sets in use at the time of that same NBC Sunday Night Football broadcast.Find the probability that at least one is is tuned to NBC Sunday Night Football (be sure to convince yourself show using the direct method and the complement method) If you had to do this by hand, which approach/calculation would you use
Answers
The probability that at least one household has their TV set tuned to the game is 1 - (1-0.22)^33, which is approximately 0.993.
To solve this problem using the direct method, we can use the fact that 22% of TV sets were tuned to the game. This means that the probability of a randomly selected TV set being tuned to the game is 0.22.
To find the probability that at least one of the 33 households surveyed had their TV set tuned to the game, we can use the complement method. The complement of the event "at least one household has their TV set tuned to the game" is "none of the households have their TV set tuned to the game".
Using the complement method, we can find the probability of this event by taking the probability that no households have their TV set tuned to the game, which is (1-0.22)^33.
So, the probability that at least one household has their TV set tuned to the game is 1 - (1-0.22)^33, which is approximately 0.993.
If I had to do this by hand, I would use the complement method, as it involves simpler calculations.
To find the probability that at least one TV set among the 33 households surveyed is tuned to NBC Sunday Night Football, we can use either the direct method or the complement method.
1. Direct Method:
The direct method requires calculating the probabilities of 1, 2, 3, ..., 33 households watching the game, and then summing up these probabilities. This method can be tedious and time-consuming, especially when done by hand.
2. Complement Method:
The complement method is generally easier and quicker, as it involves calculating the probability that none of the 33 households is watching the game and then subtracting this probability from 1.
Given that 22% (0.22) of the TV sets in use were tuned to the game, the probability that a household is not watching the game is 1 - 0.22 = 0.78.
For all 33 households not to be watching the game, the probability is (0.78)^33 ≈ 0.00038.
Now, to find the probability that at least one household is watching the game, we subtract this probability from 1:
1 - 0.00038 ≈ 0.99962.
So, the probability that at least one of the 33 households is tuned to NBC Sunday Night Football is approximately 0.99962.
If you had to do this by hand, the complement method would be the preferred approach, as it requires fewer calculations and is more straightforward.
Learn more about probability at: brainly.com/question/30034780
#SPJ11
what is 8x5? Please help me
Answers
Explanation
8 x 5 means 8 in 5 places
\(8+8+8+8+8=40\)Answer: 40
Round the following to the hundredth:
45.9563
Answers
Answer:
The answer rounded to the hundredth is 45.96.
Consider the three points, (3,7), (-6,1), and (9,y) on the same line. Find the value of y and explain your steps. Enter your response here
PLZZ HELPPP!!!!
Answers
A linear equation in the form y = mx + c has slope m Any line parallel to 3x + 9y = 5 has the same slope 3x + 9y = 5 → 9y = -3x + 5 → y = (-3/9)x + 5/9 → y = -⅓x + 5/9 &
below. a) Which of the boxes has the smaller range of masses? b) What is the value of this range? Give your answer in grams (g). Box A 97653 4 Box A Box B 15 1469 5 6 2 478 39 835 8762 7 Box B Key 35 represents a mass of 53 g 51 represents a mass of 51 g
Answers
Box B has the smaller range of masses, with a range of 49 grams, compared to Box A's range of 97,649 grams.
The question asks which of the boxes has the smaller range of masses and what is the value of this range in grams (g).
To find the range, we need to subtract the smallest value from the largest value in each box.
In Box A, the smallest value is 4 and the largest value is 97653. So, the range in Box A is 97653 - 4 = 97649 g.
In Box B, the smallest value is 2 and the largest value is 8762. However, we are given that key 35 represents a mass of 53 g and key 51 represents a mass of 51 g. So, the actual largest value in Box B is 51. Therefore, the range in Box B is 51 - 2 = 49 g.
Comparing the ranges, we can see that the range in Box B (49 g) is smaller than the range in Box A (97649 g).
For more such questions Box,Click on
https://brainly.com/question/28344846
#SPJ8
Hey pls answer this (25)

Answers
The congruent triangles in this problem are given as follows:
Triangles A and B.
What are congruent figures?Two figures are classified as congruent if their side lengths are the same.
If we rotate triangle B 180º over it's base, we have that it will have a similar format to triangle A, and also with the same side lengths.
Hence the congruent triangles in this problem are given as follows:
Triangles A and B.
With triangle C, no rotation would make it like A and B, with the same side lengths, hence it is not congruent to any of the triangles in this problem.
More can be learned about congruence of figures at https://brainly.com/question/1675117
#SPJ1
A grid shows the position of a subway stop and your house. The subway stop is located at (-10,-1) and your house is located at (-18,-16). What is the distance between your house and the subway stop?
A. 15
B. 27
C. 19
D. 17
Answers
Answer: 15
Step-by-step explanation:
Using the equation, y=5x²−17x −12, determine whether the parabola opens upward or downward.
Answers
Answer:
opens upwards
Step-by-step explanation:
given a quadratic in standard form
y = ax² + bx + c ( a ≠ 0 )
• if a > 0 then parabola opens upwards
• if a < 0 then parabola opens downwards
given
y = 5x² - 17x - 12
with a = 5 > 0
then parabola opens upward
The angle of deperession of aPt A, as measured form the top of
abuilding 30m tall is 450, how far is A from the basc of the
building?
A. 97m B. 30m C. 45m D. 32m
Answers
Answer:B
Step-by-step explanation:
Given
Height of building \(h=30\ m\)
Angle of depression \(\theta =45^{\circ}\)
Suppose distance of Point A from base of building be \(x\)
From diagram we can write
\(\Rightarrow \tan \theta =\dfrac{h}{x}\)
\(\Rightarrow \tan (45^{\circ})=\dfrac{30}{x}\)
\(\Rightarrow 1=\dfrac{30}{x}\)
\(\Rightarrow x=30\ m\)
So, point A is \(30\ m\) from base of building

Math part 2 question 4

Answers
Answer:
\(\dfrac{x}{x + 1}\\\\\text{which is the first answer choice }\)
Step-by-step explanation:
We are given
\(f(x) = x^2 - x\\g(x) = x^2 - 1\\\\\text{and we are asked to find $ \left(\dfrac{f}{g}\right)\left(x\right)$}\)
\(\left(\dfrac{f}{g}\right)\left(x\right) = \dfrac{f(x)}{g(x)}\\\\\\= \dfrac{x^2-x}{x^2 - 1}\)
\(x^2 - x = x(x - 1)\text{ by factoring out x}\\\\x&2 - 1 = (x + 1)(x - 1) \text{ using the relation $a^2 - b^2 = (a + 1)(a - 1)$}\)
Therefore,
\(\dfrac{x^2-x}{x^2 - 1} = \dfrac{x(x-1)}{(x + 1)(x - 1)}\)
x - 1 cancels out from numerator and denominator with the result
\(\dfrac{x}{x+1}\)
So
\(\left(\dfrac{f}{g}\right)\left(x\right)$} = \dfrac{x}{x + 1}\)
What can be concluded if ∠EJS and ∠SJV form a linear pair?
Answers
Answer:
They are supplementary.
Step-by-step explanation:
A linear pair consists of two opposite angles whose non-common sides create a straight line. If a linear pair consists of two angles, then they are supplementary
Show that the statement is true. If ST has endpoints S(−4, −2) and T(0, 2), then the midpoint M of ST lies on the x‐axis.
Answers
Answer:
hello there I am from India!