Answers
Answer:
3.......................
Related Questions
the solution to a system of linear equations is (0,4) one of the linear equations in the system is Y=8x+4
Answers
-> infinite number of lines can pass through a single point. We need another information do define the other line.
10 times as many as 5 tens is 5thousand
Answers
Answer:
This question does not make sense for very specific reasons
Step-by-step explanation:
1. 5,000 does not look like 5thousand
2. 10 times as many as 5 tens is not really a question at all
3. the question itself already contains the answer 5,000
What is the value of p?
O 6
O 7
08
09

Answers
Answer:
6
Step-by-step explanation:
opposite angles of a parallelogram are always congruent
36=4p+12
24=4p
p=6
can u help me with these questions

Answers
here's half of them:
1: 15 - (3r) = 6
2: q + 4f = 29
3: \(n^{2}\) + 12 = p/4
4: 0.5j - 5 = k + 13
for the rest, just know that:
sum means addition
times/product means multiplying
quotient means division
less than means subtraction
Which parent function is represented by the graph?
A. The quadratic parent function
B. The absolute value parent function
C. An exponential parent function
D. The linear parent function

Answers
Answer:
D. The linear parent function
Step-by-step explanation:
Linear functions are always characterized by a straight line graph with or without an intercept on the vertical or horizontal axis. A linear function usually has an independent variable and a dependent variable. The independent variable is commonly depicted as x while the dependent variable is y.
Thus a linear equation is an equation of the type y=ax where a is a constant term. The equation of a straight line graph his y=mx +c, where;
m= gradient of the straight line graph
x= the independent variable
y= the dependent variable
c= the vertical intercept
Answer:
The linear parent function :)
Step-by-step explanation:
A triangle is shown with its exterior angles. The interior angles of the triangle are angles 2, 3, 5. The exterior angle at angle 2 is angle 1. The exterior angle at angle 3 is angle 4. The exterior angle at angle 5 is angle 6. Which statements are always true regarding the diagram? Select three options. m∠5 + m∠3 = m∠4 m∠3 + m∠4 + m∠5 = 180° m∠5 + m∠6 =180° m∠2 + m∠3 = m∠6 m∠2 + m∠3 + m∠5 = 180°
Answers
The statements that are always true regarding the diagram are:
m∠1 + m∠5 = 180°
m∠2 + m∠3 = m∠6
m∠3 + m∠4 + m∠5 = 180°
Explain the term diagram
It refers to a value or position that is higher or greater than another value or position. It is often used in comparisons or to describe the relative positions of objects or points on a graph or coordinate plane. The opposite of "above" is "below," which refers to a value or position that is lower or lesser.
According to the given information
We know that the sum of the measures of the three interior angles of a triangle is always 180°. Therefore, we have:
m∠2 + m∠3 + m∠5 = 180°
From the given information, we know that:
m∠2 + m∠1 = 180° (linear pair of angles)
m∠3 + m∠4 = 180° (linear pair of angles)
m∠5 + m∠6 = 180° (exterior angle theorem)
Rearranging these equations, we get:
m∠1 = 180° - m∠2
m∠4 = 180° - m∠3
m∠6 = 180° - m∠5
Substituting these expressions into the above equation for the sum of the interior angles, we get:
m∠2 + m∠3 + m∠5 = m∠2 + (180° - m∠1) + m∠5
m∠3 + m∠4 + m∠5 = (180° - m∠3) + m∠4 + m∠5
Simplifying these equations, we get:
m∠1 + m∠5 = 180°
m∠2 + m∠3 = m∠6
Therefore, the statements that are always true regarding the diagram are:
m∠1 + m∠5 = 180°
m∠2 + m∠3 = m∠6
m∠3 + m∠4 + m∠5 = 180° (which is equivalent to option 2)
To know more about diagram visit
brainly.com/question/24192875
#SPJ1

Liz earns a salary of $2,200 per month, plus a commission of 5% of her sales. She wants to earn at least
$2,500 this month. Enter an inequality to find amounts of sales that will meet her goal.your
variable represents. Enter the commission rate as a decimal.
Answers
Answer:
2200 + 0.5x >= 2500
Step-by-step explanation:
x is the amount of sales
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
The table below shows the number of e-mails received each day by a
company employee for two separate weeks. If the data were represented with
a comparative dot plot, which day would have more dots for week 2 than for
week 1?
Week 1 Week 2
Monday 7 4
Tuesday 8 3
Wednesday 6
9
Thursday 9
7
Friday 5 2.
A. Wednesday
B. Tuesday
Ο Ο Ο Ο
C. Friday
D. Monday

Answers
Answer:
A. Wednesday is the correct answer
Solve using either substitution or elimination
X-3Y=-14
X-Y=-2
Answers
Explanation:
x - 3y = -14
x - y = -2
Multiply a -1 to the first equation so the x’s can cancel out.
-x + 3y = 14
x - y = -2
Subtract the two equations together.
2y = 12
y=6
Now, plug in y to one of the original equations.
x - (6) = -2
x=4
Therefore, the answer is: (4,6)
The college sold tickets to concert happening on campus and sold
1200 tickets for a total of $11,200. They sold adult tickets for $15, children
tickets for $10, and student tickets for $8. They sold three times as many
student tickets as adult and children tickets combined. How many of each type
of ticket were sold?
Answers
They sold 200 adult ticket, 100 children ticket and 900 student ticket
The college sold tickets to concert happening on campus and sold
1200 tickets for a total of $11,200
Consider the number adult ticket = x
Number of children ticket = y
Number of student ticket = z
Therefore,
x+ y+ z = 1200
They sold three times as many student tickets as adult and children tickets combined.
z = 3(x+ y)
z = 3x+3y
Substitute the values in first equation
x + y + (3x+3y) = 1200
4x+4y = 1200
x + y = 300
x+ y+ z = 1200
300+ z= 1200
z = 1200-300
z = 900 tickets
They sold adult tickets for $15, children tickets for $10 and student tickets for $8
15x + 10y +8z = 11200
Use the substitution method
15x+10y+8×900 = 11200
15x+10y = 11200-7200
15x+10y = 4000
3x+2y = 800
We know x+y = 300
x = 300-y
Then, use the substitution method
3(300-y)+2y = 800
900-3y+2y = 800
-y = 800-900
y = 100
Then,
x = 300-100
x = 200
Hence, they sold 200 adult ticket, 100 children ticket and 900 student ticket
Learn more about substitution method here
brainly.com/question/14619835
#SPJ1
Growth was wortj $42 at tje beggining of the day. event every hour stock goes down by 15%
Answers
The exponential function that represents this situation is f(x) = 42 * (0.85)ˣ
Writing the exponential function that represents this situation.From the question, we have the following parameters that can be used in our computation:
Inital growth, a = 42
Rate of decrease, r = 15%
Using the above as a guide, we have the following:
The function of the situation is
f(x) = a * (1 - r)ˣ
Substitute the known values in the above equation, so, we have the following representation
f(x) = 42 * (1 - 15%)ˣ
So, we have
f(x) = 42 * (0.85)ˣ
Hence, the function is f(x) = 42 * (0.85)ˣ
Read more about exponential function at
brainly.com/question/2456547
#SPJ1
Question
Growth was worth $42 at tje beggining of the day. event every hour stock goes down by 15%. Write the exponential function that represents this situation.
A message in a bottle is floating at the top of the ocean in a periodic manner the time between periods and maximums heights is 26 seconds and the average height of the bottle is 12 feet the bottle moves in a manner such that the distance from the highest and lowest point is 6 feet a cosine function can model the movement of the message in a bottle in Malaysian to the height Part A. Determine the amplitude and period of the function that could model the height of the message in the bottle as a function of time T Part B. assume that at T equals zero the message in a bottle is at its average height and moves upwards after what is the equation of the function that could represent the situation based on the graph of the function after how many seconds will it reach its lowest height
Answers
Part A.
We are asked to determine the amplitude and the period of the movement of the bottle. The amplitude is defined as half the distance between the highest and lowest points of the graph. Since that distance is given to be 6 feet, we have that the amplitude is:
\(A=\frac{6ft}{2}=3ft\)Therefore, the amplitude is 6ft.
The period of the movement is given to be 26 seconds.
Part B. We are asked to determine a cosine function that models the movement. A cosine function has he following general form:
\(y=Acos(bt+c)+d\)"A" is the amplitude and, in this case, is equal to 3 ft, therefore:
\(y=3cos(bt+c)+d\)The value of "d" is related to theperiod by the following relationshiop:
\(b=\frac{2\pi}{T}\)Where "T" is the period. Since the period is 26, we have:
\(b=\frac{2\pi}{26}=\frac{\pi}{13}\)Therefore, the function is:
\(y=3cos(\frac{\pi}{13}t+c)+d\)The valu of "d" is the averagae height of the motion, therefore, "d = 12ft":
\(y=3cos(\frac{\pi}{13}t+c)+12\)To determine the value of "c" we use the fact that the function starts at the average height., therefor:
\(t=0,y=12\)Substituting we get:
\(12=3cos(\frac{\pi}{13}(0)+c)+12\)We can cancel out the 12:
\(0=3cos(c)\)We divide both sides by 3:
\(cos(c)=0\)The values that satisfy this are:
\(c=\frac{\pi}{2},-\frac{\pi}{2}\)We will take the negative valuesince rwe are given that the motion goes upwards after the initial position. Therefore, we get:
\(y=3cos(\frac{\pi}{13}t-\frac{\pi}{2})+12\)And thus we get the function of the motion.
The graph is the following:
Therefore, according to the graph, the lowest height is eached atfter 19.5 seconds.

please answer thank you

Answers
Answer:
37 / 16
Step-by-step explanation:
_____________________
A rectangular prism has length 2 ft, height 7 ft, and width 4 ft.
What is the volume of the rectangular prism?
Answers
Answer:
pos no c se suma te amo
Step-by-step explanation:
gracias <3
HELP PLS !% POINTS!!

Answers
Answer:
149 sq. ft
Step-by-step explanation:
For the triangle:
Base = 16-9 = 7 ft
Area of Triangle = 1/2 of b.h
= 1/2 of 7 * 6
= 21 sq. ft
Area of Rectangle = l.b
= 5 * 16
= 128 sq. ft
Total Area = 149 sq. ft
Gavin wants to put $3,475 into a savings account when his daughter is born. Examine the account options below to determine which will have a higher accrued value at the end of 5 years.
Answers
The Capital Bank's option with a monthly compounding has a higher accrued value of $3,849.75
What is accrued value?
The accrued value in this case means accumulated amount after 5 years, in other words, the future value of the investment under each of the two options.
Daily compounding:
FV=PV*(1+r/365)^(365*N)
FV=future value=unknown]
PV=initial investment=$3,475
r=interest rate=1.90%
N=number of years=5
FV=$3,475*(1+1.90%/365)^(365*5)
FV=$3,475*(1+0.0000520547945205479)^1825
FV=$3,475*(1.0000520547945205479)^1825
FV=$3,821.31
Monthly compounding:
FV=PV*(1+r/12)^(12*N)
FV=future value=unknown]
PV=initial investment=$3,475
r=interest rate=2.05%
N=number of years=5
FV=$3,475*(1+2.05%/12)^(12*5)
FV=$3,849.75
Find out more about monthly compounding on:https://brainly.com/question/24703884
#SPJ1
Complete question:
General. Gavin wants to put $3,475 into a savings account when his daughter is born. Examine the account options below to determine which will have a higher accrued value at the end of 5 years.
Community Bank 1.90% Compounds daily
Capital Bank 2.05% Compounds monthly
Find an equation of the plane consisting of all points that are equidistant from \( (-1,-5,4) \) and \( (2,1,1) \). Note: you have to enter the full equation.
Answers
Let
�
(
�
,
�
,
�
)
P(x,y,z) be any point on the plane. Then, by the distance formula, we have:
\begin{align*}
\sqrt{(x+1)^2+(y+5)^2+(z-4)^2} &= \sqrt{(x-2)^2+(y-1)^2+(z-1)^2} \
\Rightarrow (x+1)^2+(y+5)^2+(z-4)^2 &= (x-2)^2+(y-1)^2+(z-1)^2 \
\Rightarrow x^2+2x+1+y^2+10y+25+z^2-8z+16 &= x^2-4x+4+y^2-2y+1+z^2-2z+1 \
\Rightarrow 6x+12y+6z &= -9
\end{align*}
Therefore, the equation of the plane is
2
�
+
4
�
+
2
�
=
−
3
2x+4y+2z=−3
For more questions like equation visit the link below:
https://brainly.com/question/30329863
#SPJ11
you record the number of sunny days out of a sample of 90 randomly selected days in city a and city b. in city a's sample there were 54 sunny days. in city b sample there were 63 sunny days.
Is City B significantly sunnier than City A? use a significance level of 0.05
Answers
The significance level shows that z approximately equals 1.41 for a p-value of 0.078642.
How to calculate the p-value?Based on the complete question, the sample proportion for city A will be:
= 54/90 = 0.60
The sample proportion for city B will be:
= 63/90 = 0.70
Using the table given, it can be deduced that the test statistic value will be 1.41. Therefore, the p-value will be 0.078652 in the Excel function.
Since the p-value is greater than 0.05, then we fail to reject the null hypothesis that there is no difference in the commute time.
Learn more about significance level on:
https://brainly.com/question/4599596
Find MQ.
4x - 1
12x - 17
5.
Answers
The length of MQ is 5 units.
To find MQ we have a line segment with two parts:
One represented by 4x - 1 and the other by 12x - 17.
The entire line segment, MQ, is represented by 5. To find the value of MQ, we need to set up an equation using the given terms:
(4x - 1) + (12x - 17) = 5
Now, let's solve the equation step by:
Combine like terms: 16x - 18 = 5 2.
Add 18 to both sides of the equation:
16x = 23 3.
Divide both sides by 16:
x = 23/16
Now that we have the value of x, we can find the length of MQ, which is equal to 5.
For similar question on length :
https://brainly.com/question/28108430
#SPJ11
The word isometric can be broken into two parts. The prefix "iso-” means "of the same,” and "-metric” means "measure.” How does the meaning of the word isometric relate to determining if an isometric transformation occurred? Include the defining characteristics of angle measure and line segments in your response.
Answers
The term "isometric" has the Greek roots "isos," which means "same," and "metron," which means "measure." The definition of an isometric transformation is one in which the original figure and its transformed equivalent have the same shape, size, and orientation.
When we speak about geometric figures, the concept of shape, size, and orientation come into play.The defining characteristics of angle measure and line segments play a critical role in determining whether an isometric transformation has occurred. In geometry, angle measures are the measurements of angles in a geometric figure. An angle is formed by two line segments that share a common endpoint. It is a unit used to calculate the measure of a plane figure's interior or exterior, such as a polygon. In other words, the size of the angle doesn't change during an isometric transformation.Line segments are the building blocks of geometric figures. They are used to construct geometric figures such as polygons, triangles, and rectangles, among others. In an isometric transformation, the length of the line segments remains constant because the shape and size of the original figure and its transformed equivalent remain the same.In conclusion, the word "isometric" implies that the transformation has the same measurements of the original figure. It is a transformation that retains the original geometric figures' shape, size, and orientation. The defining characteristics of angle measure and line segments remain unchanged during the isometric transformation. This means that if an isometric transformation occurs, the original and transformed figures have the same measurements of angles and line segments.For such more question on isometric
https://brainly.com/question/14486229
#SPJ8
wat is the sum of 13.75 and -11.25
Answers
Answer:
2.5
Step-by-step explanation:
Answer:
2.5
Step-by-step explanation:
use the keep change change rule
13.75 - keep
+ - change into minus
-11.25 - change into positive 11.25
Kallie works at a pet store. Part of her job is to add the correct amount of water conditioner to each fish tank the list below provides information about the number of fish tanks and the amount of water conditioner she uses.
1: there are 12 fish tanks that need water conditioner
2: Each fish tank is filled with 20 quarts of water
3: for every 10 gallon of water, Kallie uses 1 teaspoon of water conditioner
What is the total number of teaspoons of water conditioner kallie will use for all the water in 12 fish tanks?
Answers
Therefore, Kallie will need to use a total of 6 teaspoons of water conditioner for all the water in 12 fish tanks.
What is equation?An equation is a mathematical statement that shows that two expressions are equal. It consists of two sides separated by an equal sign, with the expression on the left being equal to the expression on the right. Equations are used to represent various relationships and situations in mathematics and other fields, and are solved to find the values of variables that make the equation true.
Here,
First, we need to determine the total amount of water in all 12 fish tanks. Since each fish tank is filled with 20 quarts of water, the total amount of water in all 12 fish tanks is:
12 fish tanks * 20 quarts per fish tank = 240 quarts of water
To convert quarts to gallons, we divide by 4 (since there are 4 quarts in a gallon):
240 quarts / 4 quarts per gallon = 60 gallons of water
Now, we can use the given conversion factor to determine how many teaspoons of water conditioner are needed for 60 gallons of water. Since for every 10 gallons of water, Kallie uses 1 teaspoon of water conditioner, for 60 gallons of water, she will use:
60 gallons / 10 gallons per teaspoon = 6 teaspoons of water conditioner
To know more about equation,
https://brainly.com/question/28243079
#SPJ1
PLZ HELP ME AND IF U CAN XPLAIN

Answers
Answer:
B. 1/2
Step-by-step explanation:
Slope formula = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1}}\)
\(\frac{(-4)-(-8) }{(6)-(-2)}\)
\(\frac{4}{8}\)
\(\frac{1}{2}\)
According to a survey conducted by the Association for Dressings and Sauces, 80% of American adults eat
salad once a week. A nutritionist suspects that this percentage is not accurate. She conducts a survey of
445 American adults and finds that 374 of them eat salad once a week. Use a 0.005 significance level to
test the claim that the proportion of American adults who eat salad once a week is equal to 80%.
Claim: Select an answer which corresponds to [Select an answer
Opposite: Select an answer which corresponds to [Select an answer
The test is: Select an answers
The test statistic is: z-
(to 2 decimals)
The Critical Value is: z-
Based on this we: [Select an answer
Conclusion: There Select an answer appear to be enough evidence to support the claim that the
proportion of American adults who eat salad once a week is equal to 80%.
Answers
Since the test statistic (2.53) falls within the critical values (-2.576 and 2.576), we fail to reject the null hypothesis.
How to solveTo test the claim that the proportion of American adults who eat salad once a week is equal to 80%, we will conduct a hypothesis test.
Claim: p = 0.80
Opposite: p ≠ 0.80
The test is a two-tailed z-test.
Sample proportion (p) = 374/445 = 0.8404
Test statistic= (0.8404 - 0.80) / sqrt((0.80 * (1 - 0.80)) / 445)
z = 2.53 (rounded to 2 decimals)
Significance level (α) = 0.005, so the critical values for a two-tailed test are -2.576 and 2.576.
Since the test statistic (2.53) falls within the critical values (-2.576 and 2.576), we fail to reject the null hypothesis.
Conclusion: There does not appear to be enough evidence to reject the claim that the proportion of American adults who eat salad once a week is equal to 80%.
Read more about test statistic here:
https://brainly.com/question/15110538
#SPJ1
Question 5.... plz help

Answers
Answer:
ANSWER : 4
Step-by-step explanation:
hello :
tanA=7/2 means : A= tan^-1 (7/2) =74°
List all the subsets of the given set.
{e, n, t}
Answers
The subsets of the set {e, n, t} are given as follows:
{{}, {e}, {n}, {t}, {e,n}, {e,t}, {n,t}, {e,n,t}}.
How to obtain the number of subsets in a set?Considering a set with n elements, the number of subsets in the set is the nth power of 2, that is:
\(2^n\)
The set for this problem is given as follows:
{e, n, t}
The cardinality is given as follows:
n = 3.
Hence the number of subsets is given as follows:
2³ = 8.
The subsets are given as follows:
{{}, {e}, {n}, {t}, {e,n}, {e,t}, {n,t}, {e,n,t}}.
In which {} is the empty set.
More can be learned about the subsets of a set at brainly.com/question/13458417
#SPJ1
solve for x please answer this question
Answers
Answer:
<15
Step-by-step explanation:
Translate the word phrase into an algebraic expression: sixteen times the sum of 10p and seventeen
Answers
4) Students in Ms. Udon
science class planted 13
conifers in different places
around the school yard. They
measured the heights (in inches)
of the conifers one month after
planting them. How many
conifers are greater than 6 1/4
inches tall but less than 8 1/2
inches tall?
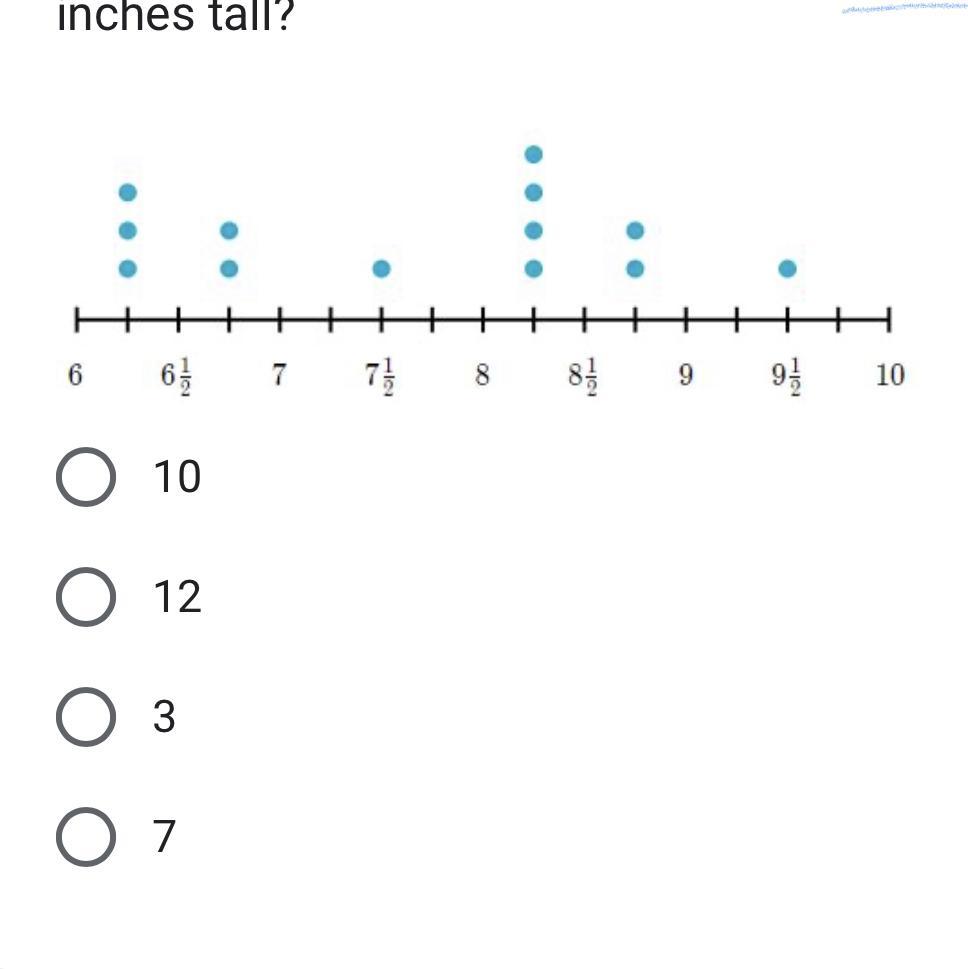
Answers
Considering the dot plot, the tallest conifer is 3.25 inches taller than the shortest conifer.
This shows, with dots, the number of times that each of the measures appears in a data set.
For finding the dot plot, we have that:
The shortest conifer measures 6 and 1/4
= 6.25 inches.
The tallest conifer measures 9.5 inches.
The difference is:
9.5 - 6.25 = 3.25 inches.
Therefore the tallest conifer is 3.25 inches taller than the shortest conifer.
More can be learned about a dot plot at;
brainly.com/question/24912483
#SPJ1
