Guys help me with that question I have a quiz after today and please explain what you did.

Answers
Answer:
a. 10 km
b. 25 km
c. 35 km
Step-by-step explanation:
You are given the rate running = 5 km per 0.5 hr and the rate for biking = 20 km per 0.8 hr. Set up a proportion to get from 0.5 hr to 1 hr multiply by 2, so multiply 5 km by 2 = 10 km. Do the same for biking 0.8 hr to 1 hr is multiplied by 1.25, so multiply 20 by 1.25 = 25 km. Add those two values together for c to get 35 km. See attached image

Related Questions
i need help with this please

Answers
Answer:
its the first one
Step-by-step explanation:
use desmos, its great for graphing this stuff

Find the slope of the line through each pair of points. 9) (17, -6), (-11,7)
(i need explanation)
I would appreciate any help.

Answers
Answer:
slope = - \(\frac{13}{28}\)
Step-by-step explanation:
calculate the slope m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (17, - 6 ) and (x₂, y₂ ) = (- 11, 7 )
m = \(\frac{7-(-6)}{-11-17}\) = \(\frac{7+6}{-28}\) = - \(\frac{13}{28}\)
Intelligence Quotient (IQ) scores are often reported to be normally distributed with μ=100. 0 and σ=15. 0. A random sample of 45 people is taken. Step 1 of 2 : What is the probability of a random person on the street having an IQ score of less than 96? Round your answer to 4 decimal places, if necessary
Answers
We are given that IQ scores are normally distributed with mean μ = 100 and standard deviation σ = 15. We want to find the probability of a random person on the street having an IQ score of less than 96.
To do this, we need to standardize the IQ score using the z-score formula:
z = (x - μ) / σ
where x is the IQ score we're interested in, μ is the mean IQ score, and σ is the standard deviation of IQ scores.
Plugging in the given values, we get:
z = (96 - 100) / 15 = -0.267
Now, we look up the probability of getting a z-score less than -0.267 in a standard normal distribution table or using a calculator. The probability is approximately 0.3944.
Therefore, the probability of a random person on the street having an IQ score of less than 96 is 0.3944 (rounded to 4 decimal places).
To know more about IQ refer here
https://brainly.com/question/29035691#
#SPJ11
Sheryl paid a plumber x dollars per hour for a 6-hour job plus $70 for parts. The total charge was $325. Which equation can be used to determine how much the plumber charged per hour?
A. 6x - 70 = 325
B. 6x + 70 = 325
C. (70 + 6)x = 325
D. (70 - 6) x = 325
Answers
The width of a rectangle measures (3s+t) centimeters,and it’s length measures (3s-9t) centimeters. Which expression represents the perimeter,in centimeters of the rectangle ?
Answers
Answer:
12s - 16t
Step-by-step explanation:
2(3s + t) + 2(3s - 9t)
6s + 2t + 6s - 18t
12s + 2t - 18t
12s - 16t
Answer:Perimeter of the rectangle =(12s -16t)centimeters.
Step-by-step explanation:
The perimeter of a rectangle is given as 2(l+w)
Given that width of the rectangle=(3s+t)centimeters. and
Length of the rectangle=(3s-9t)centimeters.
Solving we have
Perimeter= 2(l+w)
Perimeter=2(3s+t +3s-9t)
Perimeter=2(3s+3s -9t+t)
Perimeter=2(6s-8t)
Perimeter=(12s -16t)centimeters.
See related queston here : https://brainly.com/question/17288503
What is .010 as a fraction?
In math?
Answers
Answer:
\(\frac{1}{100}\)
I hope this helps!
Answer:
To write .010 as a fraction you have to write .010 as numerator and put 1 as the denominator. Now you multiply numerator and denominator by 10 as long as you get in numerator the whole number.
.010 = .010/1 = 0.1/10 = 1/100
And finally we have:
.010 as a fraction equals 1/100
hope this helps:)
List the sample space of the following chance experiment: Selecting a letter from the word statistics.
A. {s, t, a, i, c, e}
B {s, t, a, r, i, c }
C {s, t, a, l, c}
D {s, t, a, i, c}
Answers
D. {s, t, a, i, c}
The sample space must contain outcomes which are possible to obtain in a probability. Since the word 'statistics' doesn't contain letter e(A), r(B) and l(C) thus Option D is the correct answer.
Hope this helps :)
Welcome, Detective Percent. Recently, there have been many reported scams. After weeks of investigations, you finally tracked down the address of the mastermind. He is an expert in %. He knows you are here to catch him and is in the midst of destroying all the evidence. He needs 30 minutes for the whole process to complete. You have to get through all the locks (full of percentages) to get to his secret chamber before all the evidences are gone.

Answers
Answer:
filthy Frank always told ppl who had anime pic where weeaboos
the perimeter of a semicircle is 108 cm what is the perimeter of the square drawn on the diameter of the semicircle
Answers
Answer:
Step-by-step explanation:
the perimeter of the semi-circle would be the diameter plus the circumference of half of the circle.
They want to know the perimeter of a square using the diameter of the sem-circle as ONE side, so the perimeter of the square would be 4 times the ONE side.
We should recall:
diameter = 2 times the radius circumference of a cirlce = 2π r
How do we find the diameter of the of the semi circle?
The perimeter of the semi circle is given as 108 cm
Perimeter of the semicirle = 2r + π r diameter plus semi circumference
108 = r ( 2 + π) factor out the r and solve for r
108 / (2 + π) = r divide both sides by ( 2 + r)
Now we know r, the perimeter of the squqre is 4 times 2r or 8r
perimeter of square = 8 [ 108 / (2 + π) ] π I used 3.14
= 864 / 5.14
= 168.1 cm I got rounded to nearest tenth
When I re-checked by work I found a few math, logic and calculation errors. Please re-check my answer for any more mistakes.
the hypotenuse of a right triangle is 29, and the legs are consecutive numbers, what is the sum of the legs
Answers
The sides are 20 and 21 in right triangle.
What defines a right triangle?
The term "right triangle" refers to a triangle with an interior angle of 90 degrees.
The hypotenuse, the side of the right triangle that is opposite the right angle and is also its longest side, and the height and base are the two arms of the right angle.The term "right triangle" refers to a triangle with an interior angle of 90 degrees. The hypotenuse, the side of the right triangle that is opposite the right angle and is also its longest side, and the height and base are the two arms of the right angle.
29² = x² + (x+1)²
x²+ x² +2x +1 = 841
2x² +2x -840 =0
x² + x -420 =0
(x+21)(x-20)=0
x=20
the sides are 20 and 21
Learn more about right triangle
brainly.com/question/29285631
#SPJ4
last assignment due in math 4 me..
i forgot how to solve these, could anyone explain/solve one or both of these


Answers
Answer:
First one is 204 the second one is 207
Step-by-step explanation:
Mutliply width* length
6x + 7 = -5
How do you solve this? :)
Answers
Answer:
x = -2
Step-by-step explanation:
Isolate the variable, x. Note the equal sign, what you do to one side, you do to the other. Do the opposite of PEMDAS.
PEMDAS is the order of operations, and stands for:
Parenthesis
Exponents (& Roots)
Multiplications
Divisions
Additions
Subtraction
~
First, subtract 7 from both sides of the equation:
6x + 7 = -5
6x + 7 (-7) = -5 (-7)
6x = -5 - 7
6x = -12
Next, isolate the variable, x, by dividing 6 from both sides of the equation:
(6x)/6 = (-12)/6
x = -12/6
x = -2
x = -2 is your answer.
~
if a reaction occurred spontaneously and the calculated δh was positive, what must be the sign of δs? explain.
Answers
A spontaneous reaction can occur even if the calculated ΔH is positive.
When a reaction occurs spontaneously, it means that the overall change in Gibbs free energy (ΔG) is negative. ΔG represents the energy available to do useful work, and it's calculated as follows:
ΔG = ΔH - TΔS
Where T is the temperature in Kelvin. A negative ΔG indicates that the reaction is thermodynamically favorable, while a positive ΔG means that the reaction is not favorable.
To answer this question, let's rearrange the equation for ΔG:
ΔG = ΔH - TΔS
ΔH = ΔG + TΔS
Since ΔG is negative for a spontaneous reaction, we can rewrite the equation as:
|ΔH| = -ΔG + TΔS
From this equation, we can see that if ΔH is positive, then -ΔG must be greater than TΔS. Since -ΔG is negative, then TΔS must be negative as well.
In other words, a spontaneous reaction can still occur even if it absorbs heat (ΔH is positive) as long as the increase in disorder (ΔS) is negative enough to overcome the positive ΔH.
To know more about reaction here
https://brainly.com/question/28984750
#SPJ4
A pair of walkie-talkies has a 35-meter range. Anand's apartment is 18 meters
east and 19 meters north of Isaac's apartment. Isaac's apartment is at sea
level, while Anand's apartment is 7 meters above sea level. Can they use the
walkie-talkies to talk to each other from their apartments?
, because the distance between their apartments is square root meters, or to the nearest tenth, meters.

Answers
Yes, they can use the walkie-talkies to talk to each other.
The distance between them is given as 28.2 meters.
How to solve for the distance?The horizontal and vertical distances should be considered when calculating the distance between their apartments using the three-dimensional form of the Pythagorean theorem.
This comes out as \(\sqrt((18^2 + 19^2 + 7^2))\), which equals \(\sqrt(798)\) square root meters, or, to the nearest tenth, 28.2 meters.
Since this distance is less than the 35-meter range of the walkie-talkies, communication should be possible between the two apartments.
Read more about distance here:
https://brainly.com/question/2854969
#SPJ1
An airplane consumes fuel at a constant rate while flying through clear skies, and it consumes fuel at a rate of 64 gallons per minute while flying through rain clouds.
Let C represent the number of minutes the plane can fly through clear skies and R represent the number of minutes the plane can fly through rain clouds without consuming all of its fuel.
56C+64R < 9000
According to the inequality, at what rate does the airplane consume fuel while flying through clear skies, and how much fuel does it have before takeoff?
Answers
From the given inequality 56C + 64R < 9000, we know that the total amount of fuel the airplane can consume in C minutes of clear sky flying and R minutes of rain cloud flying combined is less than 9000 gallons.
Let's assume that the airplane consumes fuel at a rate of F gallons per minute while flying through clear skies.
Therefore, in C minutes of clear sky flying, the airplane consumes a total of CF gallons of fuel. Similarly, in R minutes of rain cloud flying, the airplane consumes a total of 64R gallons of fuel.
The total amount of fuel consumed by the airplane in C minutes of clear sky flying and R minutes of rain cloud flying is given by:
Total fuel consumed = CF + 64R
Since the airplane can't consume all its fuel during this time, we have:
CF + 64R < 9000/56
Simplifying the above inequality:
CF + 64R < 161.54
Now we know that the airplane can fly for C minutes through clear skies and R minutes through rain clouds without consuming all of its fuel. So, we can write:
CF + 64R = F(C + R)
Let's substitute this in the inequality we derived above:
F(C + R) < 161.54
Dividing both sides by C + R:
F < 161.54 / (C + R)
We don't have enough information to solve for F, but we do know that it must be less than 161.54 / (C + R).
To find out how much fuel the airplane has before takeoff, we need to know the total amount of fuel it can consume. We can find this by assuming that the airplane can fly for T minutes before running out of fuel, where T is the total flight time.
Let's assume that the airplane consumes fuel at a rate of F1 gallons per minute during the entire flight. Then, the total amount of fuel consumed during the flight is:
F1T
If we assume that the airplane flies only through clear skies during the entire flight, then we can use the given information to find out how much fuel it has before takeoff:
56C < F1T
Simplifying the above inequality:
C < F1T/56
Again, we don't have enough information to solve for F1 or T, so we can't find the exact amount of fuel the airplane has before takeoff.
To know more about inequality here
https://brainly.com/question/24372553
#SPJ1
PLEASE HELP ITS URGENT I INCLUDED THE GRAPHS AND WROTE THE PROBLEM DOWN!
Which graph represents the function f(x)=|x−1|−3 ?

Answers
The graph that represents the function f(x) = |x − 1| − 3 is:
Graph B
How to identify the graph of the function?To find out which graph can represent the given function f(x) = |x − 1| − 3, we need to look at each of the functions individually to deduce that.
The key to this is the point (1,-3) That point must be found first. C is incorrect because you are using 3 not - 3 which does not change (as C has changed it) through out the problem.
A is using (-1,-3) which makes it wrong. Also the equation is y = -abs(x-1) - 3 which is also a mistake. The given graph points upwards not downwards.
D has it's minimum point at (-1,-3) which is not correct.
We are left with b which opens upwards (correct) has it's min at (1,-3) [also correct] so the answer is
Read more about Function Graph at: https://brainly.com/question/24335034
#SPJ1
robin is twice as old as earl and adam is 8 years younger than earl. in 6 years robin will be three times as old as adam. find their present ages
Answers
The present age of Earl is 12 years, Robin is 24 years and Adam is 4 years old.
Let us consider the present age of Earl to be x years.
According to the given question, the present age of Robin is twice that of Earl = 2x
And since it is given that Adam is 8 years younger than Earl, then his age
= x - 8
After 6 years, the age of Earl will be x + 6
Robin's age will be = 2x + 6
Adam's age will be = x - 8 + 6 = x - 2
According to the given question, Robin's age will be thrice the age of Adam.
Hence, 2x + 6 = 3 (x - 2)
⇒ 2x + 6 = 3x - 6 ⇒ 6 + 6 = 3x - 2x ⇒ 12 = x
Thus, the present age of Earl is 12 years,
Robin's age = 2x = 2 x 12 = 24 years
Adam's age = x - 8 = 12 - 8 = 4 years
To know more about age problems:
https://brainly.com/question/29283654
#SPJ4
What i the future value of the following amount at the given imple interet rate and time 2000. 00at
3% for 3 year compounded annually
Answers
The future value of $2000 at a 3% interest rate compounded annually for 3 years would be $2185.40.
The future value calculationThe future value of $2000 at a 3% interest rate compounded annually for 3 years can be calculated using the formula:
FV = PV * (1 + r)ⁿ
where PV is the present value, r is the annual interest rate, and n is the number of compounding periods.
In this case:
FV = $2000 * (1 + 0.03)³
FV = $2000 * 1.03³
FV = $2000 * 1.0927
FV = $2185.40
So, the future value of $2000 at a 3% interest rate compounded annually for 3 years would be $2185.40.
Learn more about Future Value here:
https://brainly.com/question/14860893
#SPJ4
apply the improved euler method to approximate the solution on the interval [0, 0.2] with step size h = 0.1 to four decimal places.
Answers
After considering the given data we conclude that the solution on the interval [0, 0.2] is 1.2620
To use the Euler Method to approximate the solution on the interval [0, 0.2] with step size h = 0.1 to four decimal places, we can apply the following steps:
Describe the differential equation and initial condition: \(y' = f(x, y) = 2x + y\), y(0) = 1.
Elaborating the step size h = 0.1 and the number of steps \(n = (0.2 - 0) / h = 2.\)
Initialize the variables: \(x_{0} = 0, y_{0} = 1.\)
For i = 0 to n-1, do the following:
a. Placing the slope at (xi, yi) using f(x, y) = 2x + y: \(k_{1} = f(xi, yi) = 2xi + yi\).
b. Placing the slope at \((xi + h, yi + hk_{1} )\) using \(f(x, y) = 2x + y: k_{2} = f(xi + h, yi + hk_{1} ) = 2(xi + h) + (yi + hk_{1} ).\)
c. Placing the next value of y using the Euler Method formula: \(yi+1 = yi + h/2(k_{1} + k_{2} ).\)
d. Placing the next value of x: \(xi+1 = xi + h.\)
Rounding the final value of y to four decimal places.
Applying the above steps, we get:
\(x_{0} = 0, y_{0} = 1\)
n = 2
h = 0.1
For i = 0:
\(k1 = f(x_{0} , y_{0} ) = 2(0) + 1 = 1\)
\(k_{2} = f(x_{0} + h, y_{0} + hk_{1} ) = 2(0.1) + (1 + 0.1(1)) = 1.3\)
\(y_{1} = y_{0} + h/2(k_{1} + k_{2} ) = 1 + 0.1/2(1 + 1.3) = 1.115\)
For i = 1:
\(k_{1} = f(x_{1} , y_{1} ) = 2(0.1) + 1.115 = 1.33\)
\(k_{2} = f(x_{1} + h, y_{1} + hk_{1} ) = 2(0.2) + (1.115 + 0.1(1.33)) = 1.7965\)
\(y_{2} = y_{1} + h/2(k_{1} + k_{2}) = 1.115 + 0.1/2(1.33 + 1.7965) = 1.262\)
Hence, the approximate solution of the differential equation \(y' = 2x + y\)on the interval [0, 0.2] with step size h = 0.1 applying Euler Method is y(0.2) ≈ 1.2620 (rounded to four decimal places).
To learn more about Euler Method
https://brainly.com/question/30860703
#SPJ4
First- year high school students were randomly put into either traditional math classes or math classes taught with a new innovative approach. In a standard algebra test,230 traditionally taught students scored an average of 76.5 with a standard deviation of 7.4, while 185 students under the new approach averaged 78.8 with a standard deviation of 5.6. Is there sufficient evidence of a difference in the test results -whatis the test statistic for H0: µ1= µ2 and Ha: µ1≠ µ2?
(A) t = 76.5 - 78.8√ ((7.4)^2/230 + (5.6)^2/185)
(B) t = 2 x 76.5 - 78.8 √ ((7.4)^2/230 + (5.6)^2/185)
(C) t = 76.5 - 78.8 /((7.4)/√230 + (5.6)/√185)
(D) t = 2 x 76.5 - 78.8 /(6.5/√207.5)
(E) t = 76.5 - 78.8 /(6.5/√207.5)
Answers
The test statistic for H₀: µ₁ = µ₂ and
Hₐ: µ₁ ≠ µ₂ is t = 76.5 - 78.8√ ((7.4)²/230 + (5.6)²/185). So, the correct choice for answer is option (a).
The test statistic for a two-sample is calculated by taking the difference in the two sample means and dividing by either the pooled or unpooled estimated standard error. We have a sample of first- year high school students were randomly put into either traditional math classes or math. For first sample
Sample size, n₁ = 230
sample mean, M₁ = 76.5
Standard deviations, s₁ = 7.4
For other sample,
Sample size,n₂ = 185
Sample mean, M₂ = 78.8
Standard deviations, s₂ = 5.6
Let the population means for sample first and second be µ₁ and µ₂ respectively.
The Hypothesis testing for comparison of population meas of both samples. The null and alternative hypothesis are
H₀: µ₁ = µ₂ and
Hₐ: µ₁ ≠ µ₂
Pooled standard error = √(s₁²/n₁ + s₂²/
n₂)
= √((7.4)²/230 + (5.6)²/185)
Using the test statistic for a two-sample,
t = (( M₁ - M₂ ) -( µ₁ - µ₂))/√(s₁²/n₁ + s₂²/
n₂)
= ((76.5 - 78.8) - ( µ₁- µ₂))/√((7.4)²/230 + (5.6)²/185)
t = (76.5 - 78.8)√ ((7.4)²/230 + (5.6)²/185) ( since, µ₁- µ₂ = 0)
Hence required test statistic value is option(a). There is sufficient evidence to claim that the difference in the test results zero.
For more information about Hypothesis testing, refer:
https://brainly.com/question/29576929
#SPJ4
I need help with this

Answers
Using a trigonometric relation we will see that:
1) DE = 33.86
2) R = 20.6°.
How to work with right triangles?1) We want to get DE which is the adjacent cathetus to the given angle.
Then we can use the trigonometric relation:
tan(a) = (opposite cathetus)/(adjacent cathetus).
Here we have:
a = 21°
opposite cathetus = 13
adjacent cathetus = DE.
Replacing that we get:
DE = 13/tan(21°) = 33.86
2) Now we want to get an angle.
This time we have:
Adjacent cathetus = 24opposite cathetus = 9Using the same trigonometric relation we get:
tan(R) = 9/24
Using the inverse tangent function:
R = Atan(9/24) = 20.6°.
If you want to learn more about right triangles:
https://brainly.com/question/2217700
#SPJ1
Find the value of the monomial: 3x^2y for x=1, y=9
Answers
Answer:
Step-by-step explanation:
3x^2y
3(2)^2(9)
6^18= 101 559 956 668 416
Answer:
387,420,489 is the answer to the monomial.
Step-by-step explanation:
3x^2y = 3(1)^2(9) when the variables are replaced.
3(1) = 3
2(9) = 18
3^18 = 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3
3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 = 387,420,489
Therefore, 387,420,489 is the answer to the monomial.
Hope this helps! :D
The lifetime in hours of an electronic tube is a random variable having a probability density function given by f(x)=xexp(−x),x≥0
Answers
The probability density function (PDF) for the lifetime of an electronic tube is f(x) = x ˣ exp(-x), x ≥ 0.
What is the probability density function for the lifetime of an electronic tube?To determine the probability density function (PDF) for the lifetime of an electronic tube, we are given the function:
f(x) = x ˣ exp(-x), x ≥ 0To ensure that the PDF integrates to 1 over the entire range, we need to determine the appropriate normalization constant. We can achieve this by integrating the function over its entire range and setting it equal to 1:
∫[0,∞] f(x) dx = ∫[0,∞] (x ˣ exp(-x)) dx = 1To solve this integral, we can integrate by parts:
Let u = x, dv = exp(-x) dxThen du = dx, v = -exp(-x)
∫[0,∞] (x ˣ exp(-x)) dx = -x ˣ exp(-x) - ∫[0,∞] (-exp(-x)) dx= -x ˣ exp(-x) + exp(-x) |_0^∞= 0 + 1 = 1Therefore, the PDF is normalized, and the probability density function for the lifetime of an electronic tube is given by:
f(x) = x ˣ exp(-x), x ≥ 0Learn more about density function
brainly.com/question/31039386
#SPJ11
(Present value of an annuity) Determine the present value of an ordinary annuity of $4,500 per year for 16 years, assuming it earns 8 percent. Assume that the first cash flow from the annuity comes at the end of year 8 and the final payment at the end of year 23. That is, no payments are made on the annuity at the end of years 1 through 7 . Instead, annual payments are made at the end of years 8 through 23. The present value of the annuity at the end of year 7 is \$ (Round to the nearest cent.)
Answers
The present value of the annuity at the end of year 7 is approximately $47,069.08.
To calculate the present value of an ordinary annuity, we can use the formula:
PV = PMT * [(1 - (1 + r)⁻ⁿ) / r],
where PV is the present value, PMT is the annual payment, r is the interest rate per period, and n is the number of periods.
In this case, the annual payment is $4,500, the interest rate is 8%, and the number of periods is 16. However, the payments start at the end of year 8 and continue until the end of year 23, which means there is a delay of 7 years.
Using the formula, the present value at the end of year 7 can be calculated as:
PV = $4,500 * [(1 - (1 + 0.08)⁻¹⁶) / 0.08] = $47,069.08.
To know more about present value:
https://brainly.com/question/29140663
#SPJ4
PQ= RQ and PS= RS a=?

Answers
The measure of angle a is 15 degrees and this can be determined by using the properties of the isosceles triangle.
What are interior angles?In geometry, interior angles are formed in two ways. One is inside a polygon, and the other is when parallel lines cut by a transversal. Angles are categorized into different types based on their measurements.
Given:
The length of the segment PQ is equal to the length of the segment RQ.The length of the segment PS is equal to the length of the segment RS.The following steps can be used in order to determine the measure of angle a:
Step 1 - According to the given data, it can be concluded that triangle PQR and triangle PSR are isosceles triangles.
Step 2 - Apply the sum of interior angle property on triangle PQR.
\(\angle\text{Q}+\angle\text{P}+\angle\text{R}=180\)
\(\angle\text{Q}+2\angle\text{R}=180\)
\(2\angle\text{R}=180-60\)
\(\angle\text{R}=60^\circ\)
Step 3 - Now, apply the sum of interior angle property on triangle PSR.
\(\angle\text{P}+\angle\text{S}+\angle\text{R}=180\)
\(\angle\text{S}+2\angle\text{R}=180\)
\(2\angle\text{R}=180-90\)
\(\angle\text{R}=45^\circ\)
Step 4 - Now, the measure of angle a is calculated as:
\(\angle\text{a}=60-45\)
\(\angle\text{a}=15\)
The measure of angle a is 15 degrees.
For more information on interior angles, refer to the link given below:
https://brainly.com/question/28795639
What is the range of the function on the graph?
O. all the real numbers
O. all the real numbers greater than or equal to 0
O. all the real numbers greater than or equal to 2
O. all the real numbers greater than or equal to -3

Answers
Answer:
Last Option
All the real numbers greater than or equal to -3
Step-by-step explanation:
Range is the set of y-values that can be inputted into function f(x).
We see that our y-values range from -3 to infinity. Since -3 is closed dot, we include it in our range:
[-3, ∞) or y ≥ -3
PLEASE HELP ME WITH THIS QUESTION
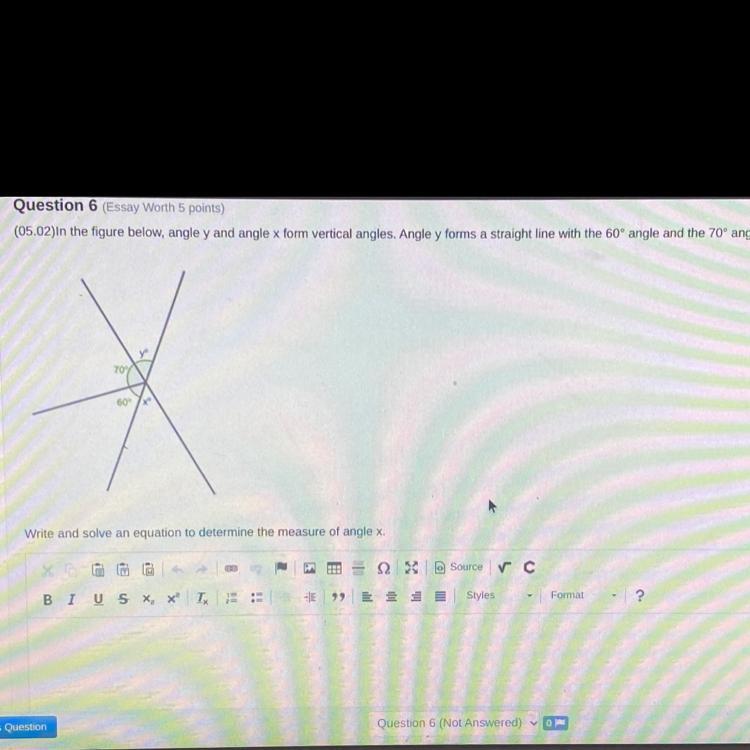
Answers
Y =50, vertical angles are congruent
X=50 degrees
The earth is approximately 90,000,000 miles from the sun. How long does it take light from the sun to reach the earth? Use the speed of light to be approximately 2 times 10^(5) miles per second.
A. 4.5 x \(10^{1}\) seconds
B. 4.5 x 10² seconds
C. 2.2 x 10² seconds
D. 4.5 seconds
Answers
\(\begin{array}{ccll} miles&seconds\\ \cline{1-2} 2\times 10^{5} & 1\\ 9\times 10^{7}& x \end{array} \implies \cfrac{2\times 10^{5}}{9\times 10^{7}}~~=~~\cfrac{1}{x}\implies (2\times 10^{5})x=9\times 10^{7} \\\\\\ x=\cfrac{9\times 10^{7}}{2\times 10^{5}}\implies x=\cfrac{9}{2}\times\cfrac{ 10^{7}}{10^{5}}\implies x=4.5\times 10^{7-5}\implies x=4.5\times 10^{2}\)
After 3 days a sample of radon-222 has decayed to 58% of its original amount. a) What is the half life of radon-222?
Answers
The half-life of radon-222 is approximately 3.84 days. We can find it in the following manner.
The half-life of a radioactive substance is the amount of time it takes for half of the initial amount of the substance to decay.
We can use the fact that the sample of radon-222 has decayed to 58% of its original amount after 3 days to determine its half-life.
Let N0 be the original amount of radon-222 and N(t) be the amount remaining after time t. We know that:
N(3) = 0.58N₀
We can use the formula for radioactive decay:
\(N(t) = N₀ * (1/2)^(t/h)\)
here h is the half-life.
Substituting in N(3) and simplifying:
\(0.58N₀ = N₀ * (1/2)^(3/h)\)
0.58 = (1/2)^(3/h)
Taking the natural logarithm of both sides:
\(ln(0.58) = ln[(1/2)^(3/h)]\)
ln(0.58) = (3/h) * ln(1/2)
h = -3 / ln(1/2) * ln(0.58)
Using a calculator, we get:
h ≈ 3.84 days
Therefore, the half-life of radon-222 is approximately 3.84 days.
Learn more about radon-222 here brainly.com/question/12498384
#SPJ4
A kitten weighed 3 3/4 ounces at birth. The kitten weighed 2 1/2 times its birth weight at the end of 2 weeks. How many ounces did the kitten weigh at the end of 2 weeks? Enter your answer in the box as a mixed number in simplest form.
Answers
Answer:
9 3/8.
Step-by-step explanation:
multiply 3 3/4 times 2 1/2.