h-(-2.22)=-7.851 solve for h
Answers
Answer:
\(\boxed {h = -10.071}\)
Step-by-step explanation:
Solve for the value of \(h\):
\(h - (-2.22) = -7.851\)
The opposite of \(-2.22\) would be \(2.22\):
\(h - (-2.22) = -7.851\)
\(h + 2.22 = -7.851\)
-Subtract both side by \(2.22\):
\(h + 2.22 - 2.22 = -7.851 - 2.22\)
\(\boxed {h = -10.071}\)
So, the value of \(h\) is \(-10.071\).
Related Questions
carl and kenna swam in opposite directions. kenna swims 1.5 times as fast as carl. in 5 minutes the swan 1500 ft. how far did each swim?
Answers
Carl swam 600 ft and Kenna swam 900 ft in 5 minutes. Let's assume that Carl's swimming speed is x ft/min. Since Kenna swims 1.5 times as fast as Carl, her swimming speed is 1.5x ft/min.
In 5 minutes, Carl swims a distance of 5x ft, and Kenna swims a distance of 5 * (1.5x) ft = 7.5x ft.
According to the given information, the total distance swum by both of them is 1500 ft. So, we can set up the equation:
5x + 7.5x = 1500
Combining like terms, we have:
12.5x = 1500
Dividing both sides of the equation by 12.5, we get:
x = 120
Therefore, Carl's swimming speed is 120 ft/min, and Kenna's swimming speed is 1.5 * 120 = 180 ft/min.
In 5 minutes, Carl swims a distance of 5 * 120 = 600 ft, and Kenna swims a distance of 5 * 180 = 900 ft.
know more about distance here:
https://brainly.com/question/15172156
#SPJ11
ed drives to work at a constant speed s. one day he is halfway to work when he immediately turns around, speeds up b8 mph, and drives home. as soon as he is home, he turns and drives to work at6 mph faster than he drove home. his total driving time is exactly 67% greater than usual. find s in mph and write the answer in the corresponding blank on the answer sheet
Answers
The speed s of Ed's drive to work is 24 mph.
Let d be the distance between Ed's home and work, and let t be the time it takes him to drive to work at speed s. Then, we know that Ed drove half the distance to work before turning around, so he drove d/2 miles.
When he turns around, he increases his speed by 8 mph, so his new speed is s+8 mph. He then drives back to his home, covering the same distance of d/2 miles at an increased speed.
The time it takes him to drive home is therefore (d/2)/(s+8) hours. When he arrives home, he turns around and drives to work at a speed of (s+6) mph. The time it takes him to drive to work is then d/(s+6) hours.
Since Ed's total driving time is 67% greater than usual, we know that his new driving time is 1.67t. Setting up an equation using these values, we get:
d/(s+6) + d/2/(s+8) + d/(s) = 1.67t
Simplifying this equation yields:
d = 6t(s+6)/(7s+24)
We also know that Ed drove half the distance to before turning around, so:
d/2 = st/2
Substituting for d and solving for s yields:
s = 24 mph
To know more about distance, refer here:
https://brainly.com/question/23366355#
#SPJ11
find an integral that represents the area inside r=4sin(θ) and outside r=2.
Answers
The integral will be the difference in the areas of the two curves: 1/2*(4sin(θ))^2 - 1/2*(2)^2.
The area inside the curve r = 4sin(θ) and outside the curve r = 2 can be represented by the integral of a certain expression.
To find the integral representing the area inside r = 4sin(θ) and outside r = 2, we need to set up an integral that calculates the area between the two curves in polar coordinates.
First, we determine the points of intersection between the two curves. Setting r = 4sin(θ) equal to r = 2, we can solve for the values of θ where the curves intersect. By analyzing the equation, we find that the curves intersect at θ = π/6 and θ = 5π/6.
Next, we set up the integral to calculate the desired area. The integral will have limits from θ = π/6 to θ = 5π/6, as this covers the region between the curves. The integral will be the difference in the areas of the two curves: 1/2*(4sin(θ))^2 - 1/2*(2)^2.
Evaluating this integral will yield the area inside r = 4sin(θ) and outside r = 2. By calculating the integral over the specified range of θ, the result will provide the desired area.
Learn more about area here:
https://brainly.com/question/27683633
#SPJ11
133 chocolates are given to two students, student A recieves 19 more chocolates than student B, which is the ecuation needed to know the amount of chocolates given to student B?
Answers
Find a particular solution to the differential equation using the Method of Undetermined Coefficients.
(d2y/dx2)-5(dy/dx)+8y = xex
Answers
r^2 - 5r + 8 = 0
The roots of this equation are r1 = 2 and r2 = 4.
Therefore, the general solution to the homogeneous equation is:
y_h = c1e^(2x) + c2e^(4x)
Now, we need to find a particular solution to the non-homogeneous equation.
Since the right-hand side of the equation is xex, which is a product of a polynomial and an exponential function, we can assume a particular solution of the form:
y_p = (Ax + B)ex
Taking the first and second derivatives of y_p:
y_p' = Aex + (Ax + B)ex
y_p'' = 2Aex + (Ax + B)ex
Substituting these expressions into the differential equation:
2Aex + (Ax + B)ex - 5(Aex + (Ax + B)ex) + 8(Ax + B)ex = xex
Simplifying:
(-3A + 8B)ex = xex
Therefore, we have:
-3A + 8B = x
To solve for A and B, we differentiate y_p:
y_p' = Aex + (Ax + B)ex
y_p'(0) = A + B = 0
Therefore, B = -A.
Substituting this into the equation -3A + 8B = x, we get:
-3A + 8(-A) = x
Solving for A, we get:
A = -x/5
Substituting this into B = -A, we get:
B = x/5
Therefore, the particular solution to the differential equation is:
y_p = (-x/5 + x/5)ex = (0)ex = 0
The general solution to the non-homogeneous equation is:
y = y_h + y_p = c1e^(2x) + c2e^(4x)
Therefore, the general solution to the differential equation is:
y = c1e^(2x) + c2e^(4x)
How do I solve this equation?

Answers
The solution of the equation is ( x - 5 )² +23 = 0.
What is completing square method?Completing the square entails writing a quadratic in the form of a squared bracket and, if necessary, adding a constant.
Mathematical symbols can represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping, as well as the order of operations and other features of logical syntax.
Given that the equation is x²-10x = 3. The equation will be solved by completing the square method as below,
x²-10x = 3
x² - 10x - 3 = 0
( x - 5 )² - 3 + 5² = 0
( x - 5 )² - 3 + 25 = 0
( x - 5 )² + 23 = 0
To know more about completing the square method follow
https://brainly.com/question/13981588
#SPJ1
2 1/3:4 1/2 write the ratio as a fraction in simplest form
Answers
Answer:
14/27
Step-by-step explanation:
7/3 ÷ 9/2
7/3 x 2/9 = 14/27
Warm up: solve for the variable
3 = x/5
Answers
Answer:
x=15
Step-by-step explanation:
multiply 5 by both sides to get rid of 5 on the second side --> 3x5=x/5x5
15=x
ur wecome :)
brainliest please?

using the information given, select the statement that can deduce the line segments to be parallel. if there are none, then select none. when m8
Answers
Based on the image below, if ∠8 = ∠4, then AD is parallel to BC using the concept of alternate interior angles.
When two parallel lines are crossed by a transversal, the pair of angles formed on the inner side of the parallel lines, but on the opposite sides of the transversal are called alternate interior angles. These angles are always equal.
The converse is also true. If a pair of angles formed on inner side of two lines, but on opposite side of transversal are equal, then the two lines are said to be parallel.
Learn more about alternate interior angles here
https://brainly.com/question/29114209
#SPJ4

What is the range of the function f(x) = -3x + 1 when the domain is {-2, 0, 3}?
A. all real numbers
B. {-31, -29, -32}
C. {7, 1, -8}
D. {-5, 1, -8}
Answers
Answer:
Solution given:
f(x) = -3x + 1
f(-2)=-3×-2+1=7
f(0)=-3×0+1=1
f(3)=-3×-3+1=-8
So
Range is {7,1,-8) is a required answer
Levi invested $5,300 in an account paying an interest rate of 2.4% compounded daily. Assuming no deposits or withdrawals are made, how much money, to the nearest cent, would be in the account after 6 years?
Answers
making the assumption that "daily" will stand for 365days per year, so the compounding period will just be 365, so
\(~~~~~~ \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+\frac{r}{n}\right)^{nt} \quad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill &\$5300\\ r=rate\to 2.4\%\to \frac{2.4}{100}\dotfill &0.024\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{assuming a 365days year} \end{array}\dotfill &365\\ t=years\dotfill &6 \end{cases} \\\\\\ A=5300\left(1+\frac{0.024}{365}\right)^{365\cdot 6}\implies A\approx 6120.86\)
Expand the following expression 3(4 − 5x)
Answers
Answer:
12-15x
Step-by-step explanation:
What ordered pairs are the solutions of the system of equations shown in the graph below?

Answers
The ordered pairs which give the solutions of the system of equations are (-4, 1) and (-8, 9)
How to determine what ordered pairs are the solutions of the system of equations?In order to determine the ordered pairs which give the solutions of the system of equations in a linear-quadratic graph, you need to find the points of intersection of the line and curve from the graph.
Then trace to the x and y-axes to find the ordered pairs values (Check the image attached)
Thus, the ordered pairs are (-4, 1) and (-8, 9)
Learn more about system of equations on:
brainly.com/question/13729904
#SPJ1

NEED HELP! John wrote the numbers 678,901 and 67,890. How many times greater is the value of 7 in 678,901 than the value of 7 in 67,890?A. 10,000B. 1,000C. 100D. 10
Answers
70,000 / 7,000 = 10
N. 1 and 7/10 gallons of gasoline were used to drive 25 and 1/2 miles. How many
miles per gallon did the car get?
miles per gallon
Answers
Answer:
Similar to the question: They figure that they will drive 792 miles round trip. If their car gets 25 miles per gallon and the current cost of gasoline is $2.35, what will the gas for their trip cost? $74.45 George is taking the same trip to San Antonio (792 miles)
Step-by-step explanation:
Hope it helps :)
Joyce is training for the upcoming marathon and trains every morning at the local track (400 m). If she runs around the track 12 times, what is her displacement? (Remember to include the units)
Answers
Answer:
Step-by-step explanation:
4,800 cm Units
In Example 5.4 that begins. you and two friends decided to go to Wendy's. Now, suppose that instead you go to Burger King, which recently filled approximately 90.9% of orders correctly. What is the probability that a. all three orders will be filled correctly? b. none of the three will be filled correctly? c. at least two of the three will be filled correctly? d. What are the mean and standard deviation of the binomial distribution used in (a) through (c)? Interpret these values. e. Compare the results of (a) through (d) with those of Wendy's in Example 5.4 and McDonald's in Problem 5.17
Answers
a. The probability that all three orders will be filled correctly at Burger King is approximately 0.738.
b. The probability that none of the three orders will be filled correctly at Burger King is approximately 0.008.
c. The probability that at least two of the three orders will be filled correctly at Burger King is approximately 0.963.
d. The mean and standard deviation of the binomial distribution used in parts (a) through (c) are approximately μ = 2.727 and σ = 0.733, respectively.
a. The probability that all three orders will be filled correctly at Burger King, which has a 90.9% success rate, can be calculated using the binomial distribution.
P(all three orders filled correctly) = (0.909)^3 = 0.738
b. The probability that none of the three orders will be filled correctly can also be calculated using the binomial distribution.
P(none of the three orders filled correctly) = (1 - 0.909)^3 = 0.008
c. To calculate the probability that at least two of the three orders will be filled correctly, we can subtract the probability of none of the orders being filled correctly and the probability of exactly one order being filled correctly from 1.
P(at least two orders filled correctly) = 1 - P(none filled correctly) - P(one filled correctly)
P(at least two orders filled correctly) = 1 - 0.008 - 3 * (0.909)^1 * (1 - 0.909)^2 = 0.963
d. The mean (μ) and standard deviation (σ) of a binomial distribution are calculated as follows:
μ = n * p
σ = sqrt(n * p * (1 - p))
Where:
n = number of trials (3 in this case)
p = probability of success (0.909)
μ = 3 * 0.909 = 2.727
σ = sqrt(3 * 0.909 * (1 - 0.909)) = 0.733
The mean represents the average number of successful orders, which is approximately 2.727. The standard deviation indicates the spread or variability of the distribution, which is approximately 0.733.
To know more about the binomial distribution, refer here:
https://brainly.com/question/29163389#
#SPJ11
Help pls. i need to get math grade up or i will fail pls!
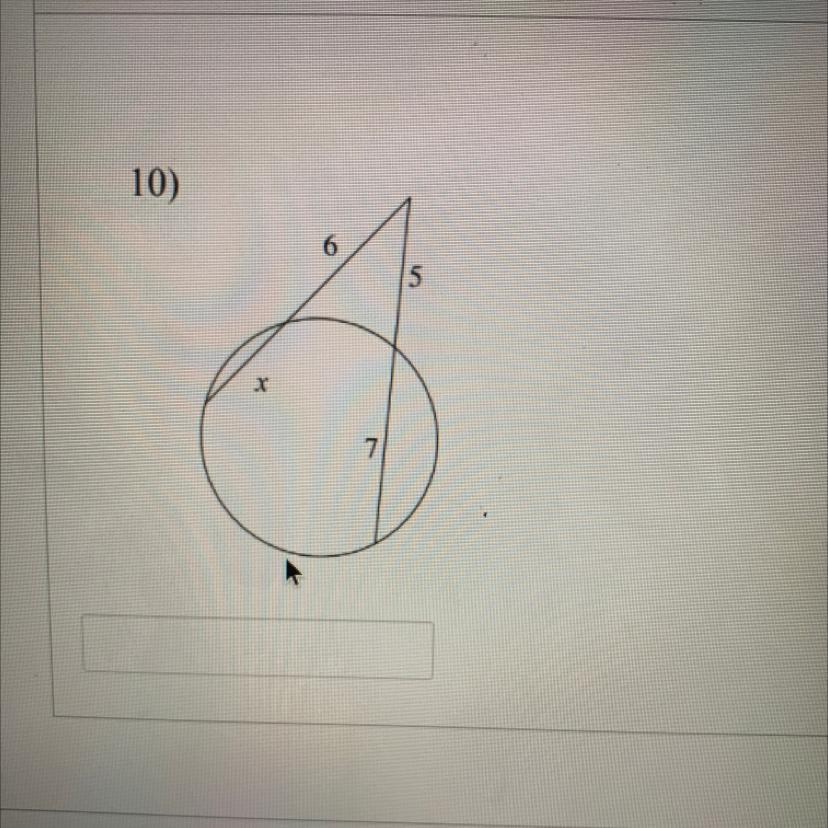
Answers
The numerical value of x in the secant line is 4.
What is the numerical value of x in the figure?The Intersecting Secants Theorem states that "when secants intersects, their line segments are in proportion.
Its is expressed as:
Segment AB × segment AC = segment AD × segement AE.
From the image of the intersecting secants:
Let:
6 = segment AB
x + 6 = segment AC
5 = segment AD
5 + 7 = segment AE
Now, these values into the above formula:
Segment AB × segment AC = segment AD × segement AE.
6 × ( x + 6 ) = 5 × ( 5 + 7)
Solve for x
6x + 36 = 25 + 35
6x + 36 = 60
6x = 60 - 36
6x = 24
x = 24/6
x = 4
Therefore, the value of x is 4.
Learn more about Secants Theorems here: https://brainly.com/question/30242636
#SPJ1
Please i have a few more minutes

Answers
The theoretical probability of rolling a sum of 7 on two dice is 1/6, or 16.67%.
The theoretical probability of rolling a sum of 9 is 1/36, or 2.78%. Again, the experimental probability of rolling a sum of 9 is determined by actually rolling two dice and recording the results. This can be done numerous times to determine the likelihood of rolling a sum of 9. To calculate the theoretical probability of rolling a sum of 7 or 9, we can add the two probabilities together. The theoretical probability of rolling a sum of 7 or 9 will be 1/6 + 1/36 = 17/36, or 47.22%. To calculate the experimental probability of rolling a sum of 7 or 9, we can add the results of the two dice rolls together. We can then record the number of times that the sum of the two dice is 7 or 9. The experimental probability of rolling a sum of 7 or 9 will be the number of times a sum of 7 or 9 was rolled, divided by the total number of rolls.
Therefore, the theoretical probability of rolling a sum of 7 or 9 is 47.22%, while the experimental probability of rolling a sum of 7 or 9 will vary depending on the number of rolls taken.
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ1
36) How old am I if 500 reduced by 3 times
my age is 299?
Answers
Answer:
67
Step-by-step explanation:
500 − 3x = 299
3x = 201
x = 67
calculate the solar flux density (also known as the solar constant) for mercury using the following information: solar luminosity = 3.865 x 10^26 w distance of mercury from the sun = 5.791 x 10^10 m
Answers
Therefore, the solar flux density for mercury after the calculation is 9.12 x 10⁻³ W/m².
The solar flux density also referred to as the solar constant is the total amount of energy derived from the sun per unit area per given unit of time. It is considered to be equal to solar luminosity divided by the surface area of a given sphere that has a radius equivalent to the distance between the respective planet from the sun.
using the formula for finding the solar flux density,
solar flux density = solar luminosity /(4 x π x distance between mercury and the sun)
solar flux density = 3.865 x \(10^{26}\) /(4 x π x ( 5.791 x \(10^{10}\)))
solar flux density = 9.12 x 10⁻³ W/m²
Therefore, the solar flux density for mercury after the calculation is 9.12 x 10⁻³ W/m².
To learn more about solar flux density,
https://brainly.com/question/14891737
#SPJ4
Evaluate the exponential expression. 14^2
Answers
Answer:196
Step-by-step explanation:
Answer:
196
Step-by-step explanation:
Exponential expressions are just a way to write powers in short form. The exponent indicates the number of times the base is used as a factor. So in the case of 32, it can be written as 2 × 2 × 2 × 2 × 2=25, where 2 is the “base” and 5 is the “exponent”. We read this expression as “two to the fifth power”.
The parabola opens _______, therefore the vertex will be a __________. The vertex is located at the coordinates ( , ), which means it moved ______ units _______. The parabola will be wider/narrower than y=x2because ______________________________.
Answers
The width of a parabola is determined by the value of a, the coefficient of the quadratic term. If a is greater than 1, the parabola will be narrower than y = x².
How to solve the parabola?
The statement "the parabola opens" can have different endings depending on the specific equation of the parabola. However, in general, a parabola can open upwards or downwards. If the coefficient of the quadratic term (x²) is positive, the parabola opens upwards, and if it is negative, the parabola opens downwards.
The vertex of a parabola is the point at which the curve changes direction. For a parabola opening upwards, the vertex is the lowest point on the curve, and for a parabola opening downwards, the vertex is the highest point on the curve. Therefore, if the parabola opens upwards, the vertex will be a minimum point, and if it opens downwards, the vertex will be a maximum point.
The vertex of a parabola is located at the coordinates (h, k), where h is the x-coordinate and k is the y-coordinate. To find the vertex, one can use the formula h = -b/2a and k = f(h), where a, b, and c are the coefficients of the quadratic equation f(x) = ax² + bx + c.
If the vertex of a parabola is at (h, k), then the parabola has been shifted h units horizontally and k units vertically from the standard position of y = x². If h is positive, the parabola has shifted to the right, and if it is negative, the parabola has shifted to the left. If k is positive, the parabola has shifted upwards, and if it is negative, the parabola has shifted downwards.
The width of a parabola is determined by the value of a, the coefficient of the quadratic term. If a is greater than 1, the parabola will be narrower than y = x², and if a is less than 1, the parabola will be wider than y = x². If a is negative, the parabola will be inverted compared to y = x², but the same principles apply.
In summary, the opening direction of a parabola, the type of vertex, the location of the vertex, the amount of horizontal and vertical shift from the standard position, and the width of the parabola are all determined by the coefficients of the quadratic equation.
To know more about parabola visit :-
https://brainly.com/question/29635857
#SPJ1
solve the algebraic equation below
(9x2x2+6x+5)+(3x2-5x-9)
Answers
Answer:
x+38
Step-by-step explanation:
ok so try to understand my explaination!
it goes by simplifying one by one :)
(18*2+6x+5)+(3*2-5x-9)
(41+6x)+(-3-5x)
41+6x-3-5x
41-3=38
6x-5x=(1)x
x+38
try to understand, im not amazing at explaining :)
If f(x) = |x – 1] + 2 is changed to g(x) = -2f(x) + 8, how is the graph of the function transformed?
Answers
we have
f(x) = |x – 1] + 2
g(x) = -2f(x) + 8
substitute the value of f(x) in g(x)
so
g(x)=2(|x – 1] + 2) +8
g(x)=2|x – 1] + 4 +8
g(x)=2|x – 1] + 12
Using a graphing tool
see the attached image
![If f(x) = |x 1] + 2 is changed to g(x) = -2f(x) + 8, how is the graph of the function transformed?](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/KdOPBkvZZ5rR5FBun6i2q68klS0q5rDZ.jpeg)
Isaac owns a home, has a bi-weekly gross income of $1,925. 00,
and has total minimum monthly debt payments of $3,915. 0.
Choose the inequality that shows the minimum amount Isaac
needs to reduce his monthly debt payments by to have a debt-to-
income ratio of 35%.
x≤ $1,459. 79
x ≥ $1,459. 79
x≤ $2,455. 21
x ≥ $2,455. 21
Answers
The inequality that shows the minimum amount of Isaac is x ≥ $2,455.21
What is inequality?
An inequality is a mathematical statement that compares two expressions and expresses the relationship between them. It is represented by a symbol such as ">", "<", "≥", or "≤" and can be thought of as a generalization of an equation.
First, we need to find Isaac's monthly gross income. Since he has a bi-weekly gross income of $1,925, we can calculate his monthly gross income as follows:
Monthly gross income = bi-weekly gross income x 26 / 12 = $1,925 x 26 / 12 = $4,158.33
The debt-to-income ratio is the ratio of monthly debt payments to monthly gross income, expressed as a percentage.
We want to find the minimum amount by which Isaac needs to reduce his monthly debt payments to have a debt-to-income ratio of 35%.
So we can set up the following inequality:
Minimum monthly debt payments / Monthly gross income ≤ 35% / 100%
Substituting the given values, we get:
$3,915 / $4,158.33 ≤ 0.35
Simplifying this inequality, we get:
0.9407 ≤ 0.35
This inequality is not true, so we made an error in our calculations. Let's check the calculation of monthly gross income. We should have:
Monthly gross income = bi-weekly gross income x 26 / 12 = $1,925 x 26 / 12 = $4,158.33
This calculation is correct. The problem is that the minimum monthly debt payments of $3,915 are already higher than what is allowed by the debt-to-income ratio of 35%. In fact, the maximum monthly debt payments Isaac can have to satisfy the 35% debt-to-income ratio is:
Maximum monthly debt payments = Monthly gross income x 35% = $4,158.33 x 35% = $1,454.92
Therefore, the minimum amount by which Isaac needs to reduce his monthly debt payments is:
$3,915 - $1,454.92 = $2,460.08
Rounding this to two decimal places, we get $2,460.09, which is closest to the fourth option:
x ≥ $2,455.21
Hence, the inequality that shows the minimum amount of Isaac is x ≥ $2,455.21
To learn more about inequality visit:
https://brainly.com/question/30238989
#SPJ1
CAN SOMEONE HELP ME WITHOUT SENDING LINKS

Answers
Answer:
Below.
Step-by-step explanation:
The slope = difference of y values/ difference of x values
13. Slope = (-5-5)/(-3-2)
= -10/-5
= 2.
14. Slope = (-8-8)/(7-9)
= -16/-2
= 8.
Question is in the image. I need help with #19

Answers
EXPLANATION
Replacing the given functions into the following:
\(\frac{f(x+h)-f(x)}{h}\)\(\frac{x^2-1+h-(x^2-1)}{h}\)Removing the parentheses and simplifying:
\(\frac{x^2-1+h-x^2+1}{h}\)Simplifying like terms:
\(\frac{h}{h}=1\)Hence,
\(\frac{f(x+h)-f(x)}{h}=1\)A) For a data set with 10 classes that ranges from 25 to 200, what would be an appropriate class interval?
b) For a data set with 230 observations, how many classes should you have?
c) Where would the 60th percentile be located in a data set with 120 observations? (Side Note: Sometimes The number is not a whole number. In that case, count to the position of the leading number first, then multiply the difference between that number and the next number by the decimal portion.)
for C) The number I got was 72.6 but I dont know what to do after that. its not the right answer
Answers
Answer:
a) To determine the appropriate class interval for a dataset with 10 classes that ranges from 25 to 200, we can use the following formula:Class Interval = (Max Value - Min Value) / Number of ClassesClass Interval = (200 - 25) / 10Class Interval = 17.5Therefore, an appropriate class interval for this dataset would be 17.5.
b) To determine the number of classes for a dataset with 230 observations, we can use the following formula: Number of Classes = √(Number of Observations)Number of Classes = √(230)Number of Classes = 15.165So we should have around 15-16 classes.
c) To determine the location of the 60th percentile in a dataset with 120 observations, we can use the following formula:60th Percentile = (Percentile Rank / 100) x Number of Observations60th Percentile = (60 / 100) x 12060th Percentile = 72Therefore, the 60th percentile is located at the 72nd observation.
please help me 10 – 2x
Answers
Answer:9x-10=2x+1
Step-by-step explanation: i think.