Answers
Answer:
Many solutions
Step-by-step explanation:
:)))))))))
Related Questions
Find the slope of the line that goes through (0,2) and (4,-2)

Answers
y2 - y1/x2 - x1
We take the second y minus the first y
over the second x minus the first x.
So we have -2 - 2/4 - 0.
Simplifying from here, we have -4/4.
This reduces to -1.
So the slope of the line is -1.
How i can answer this question, NO LINKS, if you answer correctly i will give u brainliest!

Answers
Answer:
Just right
Step-by-step explanation:
BRAIN PLS
You buy a house including the land it sits on for $145000. The real estate agent tells you that the land costs $25000 more than the house. The price of the house is $ ___ and the price of the land is $ ___.
Answers
The price of the house is $60,000, and the price of the land is $85,000.
Let's denote the price of the house as x. According to the information given, the land costs $25,000 more than the house. This means the price of the land is x + $25,000.
The total price of the house and land together is $145,000. So we can form the equation: x + (x + $25,000) = $145,000.
Simplifying the equation, we have: 2x + $25,000 = $145,000.
By subtracting $25,000 from both sides of the equation, we get: 2x = $120,000.
Dividing both sides by 2, we find: x = $60,000.
Therefore, the price of the house is $60,000. Substituting this value back into the equation for the price of the land, we have: $60,000 + $25,000 = $85,000.
Hence, the price of the land is $85,000.
Learn more about price here
https://brainly.com/question/19091385
#SPJ11
If EFG ≅ △ ABD
so FG is
= .......?
help asap
Answers
Answer:
FG=BD
Step-by-step explanation:
hope this helps!!
PLESSS help me I'm begging you
Answers
To find the volume of each pris you multiply the measures
So
first prism
\(15\operatorname{cm}\times12\operatorname{cm}\times5\operatorname{cm}\)then first blanck is 12
Second prism
\(5\operatorname{cm}\times14\operatorname{cm}\times4\operatorname{cm}\)if we multiply 5 and 14
\(70sq\operatorname{cm}\times4\operatorname{cm}\)then second blanck is 70
Total volume
\(\begin{gathered} (15\operatorname{cm}\times12\operatorname{cm}\times5\operatorname{cm})+(70sq\operatorname{cm}\times4\operatorname{cm}) \\ 900+280=1180 \end{gathered}\)then last blanck is 1180cu cm
Part A
Which equation can be used to determine the total cost, y, for a tickets ordered in a transaction?
O y = 2.25x + 15.50
O y = 15.50x +2.25
x = 2.25y + 15.50
O = 15.50y +2.25
Part B
If the total cost of a transaction is $157.25, how many movie tickets were ordered?
Enter the correct answer in the box
tickets:
Answers
a) The equation that can be used to determine the total cost, y, for a tickets ordered in a transaction is y = 15.50x + 2.25
b) The number of movie tickets sold is x = 10 tickets
What do you mean by an Equation?Equations are statements in mathematics that have two algebraic expressions on either side of the equals (=) sign.
It displays the similarity of the connections between the phrases on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are examples of the parts of an equation. When creating an equation, the "=" symbol and terms on both sides are necessary.
Given data ,
Let the total cost of the movie be represented as y
Let the number of tickets sold be x
Now , the cost of one movie ticket = $ 15.50
And , the cost of x tickets = $ 15.50x
The cost of the transaction = $ 2.25
So , the total cost y = cost of x tickets + cost of the transaction
On simplifying the equation , we get
y = 15.50x + 2.25 be equation (1)
b)
Let the number of tickets be x
Now , the total cost of the transaction is y = $ 157.25
So , y = 15.50x + 2.25
On simplifying , we get
157.25 = 15.50x + 2.25
Subtracting 2.25 on both sides , we get
15.50x = 155
Divide by 15.5 on both sides , we get
x = 10 tickets
Hence , the number of tickets sold is 10 tickets
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ9
The complete question is attached below :
Part A
Which equation can be used to determine the total cost, y, for a tickets ordered in a transaction?
O y = 2.25x + 15.50
O y = 15.50x +2.25
x = 2.25y + 15.50
O = 15.50y +2.25
Part B
If the total cost of a transaction is $157.25, how many movie tickets were ordered?

Find the result of |x-1|=2
Answers
The absolute value of x minus one is equal to two. Therefore, x must be either one greater than two (x = 3) or one less than two (x = 1).
One less than x results in a value of two in absolute terms. As a result, x minus 1 has an absolute value of 2, which is a positive number. The separation of an integer from zero is its absolute value. As a result, x minus 1 is two units from zero in absolute terms. As x minus one has an absolute value of two, its real value must either be two or a negative two. That is to say, x must either be one more than two (x = 3) or one less than two (x = 1).In order to confirm this, let's look at a few examples. If x = 3, then |x - 1| = |2 - 1| = |1| = 1 which is not equal to two. Therefore, x = 3 is not the answer we are looking for. On the other hand, if x = 1, then |x - 1| = |1 - 1| = |0| = 0 which is not equal to two. Therefore, x = 1 is also not the answer we are looking for. The only two possible solutions for the equation |x - 1| = 2 are x = 3 and x = 1. Therefore, the result of |x - 1| = 2 is that x must be either one greater than two (x = 3) or one less than two (x = 1)
Learn more about absolute value here
https://brainly.com/question/1301718
#SPJ4
Sketch the following and then find the sum of the vertex
angles.
a. A hexagon
b. An octagon
c. A dodecagon.
Answers
To find the sum of the vertex angles in various polygons, we need to sketch the polygons and then calculate the sum. For a hexagon, octagon, and dodecagon, the sums of the vertex angles are 720°, 1,080°, and 1,800°, respectively.
a. Hexagon: A hexagon is a polygon with six sides. To find the sum of the vertex angles, we can divide the hexagon into triangles. Since each triangle has an interior angle sum of 180°, the hexagon can be divided into four triangles. Therefore, the sum of the vertex angles in a hexagon is 4 * 180° = 720°.
b. Octagon: An octagon is a polygon with eight sides. Similar to the hexagon, we can divide the octagon into triangles. Dividing it into six triangles, each with an interior angle sum of 180°, the sum of the vertex angles in an octagon is 6 * 180° = 1,080°.
c. Dodecagon: A dodecagon is a polygon with twelve sides. Dividing it into ten triangles, each with an interior angle sum of 180°, the sum of the vertex angles in a dodecagon is 10 * 180° = 1,800°.
Therefore, the sum of the vertex angles in a hexagon is 720°, in an octagon is 1,080°, and in a dodecagon is 1,800°.
Learn more about polygons here:
https://brainly.com/question/23846997
#SPJ11
Find the sum of the vertex angles of the following polygons---
a. A hexagon
b. An octagon
c. A dodecagon.
test the series for convergence or divergence using the alternating series test. [infinity] (−1)n − 1 5n 6 n = 1
Answers
The series ∑((-1)⁽ⁿ⁻¹⁾ * 5n)/(6n) from n = 1 to infinity converges based on the alternating series test.
To test the series for convergence or divergence using the alternating series test, we need to check if the terms of the series alternate in sign and if their absolute values decrease as n increases.
The series is given by:
∑((-1)⁽ⁿ⁻¹⁾ * 5n)/(6n) from n = 1 to infinity
Let's analyze the terms of the series:
Alternating sign: The terms alternate between positive and negative because of the (-1)⁽ⁿ⁻¹⁾ factor.
Decreasing absolute values: We can simplify the terms by canceling out the common factors of 5 and 6:
((-1)⁽ⁿ⁻¹⁾ * 5n)/(6n) = (-5/6)ⁿ
The absolute values of the terms are decreasing because
|(-5/6)ⁿ| < |(-5/6)⁽ⁿ⁻¹⁾ | for all n.
Since the series satisfies the conditions of the alternating series test, namely alternating sign and decreasing absolute values, we can conclude that the series converges.
To know more about convergence or divergence, visit:
https://brainly.com/question/32762259
#SPJ11
you spin the spinner once what is p(greater than 2 or less than 2 write your answer as a percentage rounded to the new tenth
Answers
For the given problem, The probability of getting a number greater than 2 or less than 2 on the spinner, rounded to the nearest tenth, can be given by 83.3%.
How to calculate required probability?The given spinner will have four numbers larger than two, i.e. 3, 4, 5, and 6.
While, there is only one number on the given spinner that is less than 2, i.e. 1.
So, the total number of favorable outcomes (numbers greater than 2 or less than 2) is 4 + 1 = 5.
Since there are a total of 6 equally likely possible outcomes (numbers 1 through 6 on the spinner), the probability of getting a number greater than 2 or less than 2 would be 5 out of 6 as:
\(Probability = \text{(Number of favorable outcomes / Total number of possible outcomes) * 100}\\\\Probability = (5 / 6) * 100\\\\Probability = 83.3\%\)
Learn more about Probability here:
https://brainly.com/question/12629667
#SPJ1
The answer is 100%, rounded to the nearest tenth.
What is probability?
Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain to happen.
If the spinner has equally likely outcomes, then the probability of getting a number greater than 2 or less than 2 is 1, since every number on the spinner is either greater than 2 or less than 2.
When we spin a spinner with equally likely outcomes, each possible outcome has the same chance of occurring. In this case, the spinner has numbers from 1 to 4, and half of these numbers are greater than 2 and half are less than 2.
Therefore, if we want to find the probability of getting a number that is greater than 2 or less than 2, we simply add up the probabilities of these two events, which gives us 1 (or 100% as a percentage).
So, the answer is 100%, rounded to the nearest tenth.
To learn more about probability from the given link:
https://brainly.com/question/30034780
#SPJ1
(number 12)
Trapezoid CDEF with vertices C(-6,6), D(-2,8), E(1,2), and F(-5,4):
(a) Translation: (x,y) —> (x-2, y-8)
(b) Rotation: 270° counterclockwise
i’ll rate u very good or however u use this app lol

Answers
The trapezoid C'D'E'F' has been rotated 270° counter-clockwise about the origin to a new position C''D''E''F''.
What is translation?Translation is a geometric transformation that moves an object from one position to another without changing its size, shape, or orientation.
According to question:a) Translation:
To perform a translation of the trapezoid, we need to subtract 2 from the x-coordinates and subtract 8 from the y-coordinates of each vertex. The vertices' new coordinates are:
C(-6,6) -> C'(-8,-2)
D(-2,8) -> D'(-4,0)
E(1,2) -> E'(-1,-6)
F(-5,4) -> F'(-7,-4)
The trapezoid CDEF has been translated 2 units left and 8 units down to a new position C'D'E'F'.
b) Rotation:
To perform a rotation of the trapezoid, we need to rotate each vertex 270° counter-clockwise about the origin. To do this, we can use the following transformation matrix:
[ cos(270°) -sin(270°) ]
[ sin(270°) cos(270°) ]
= [ 0 -1 ]
[ 1 0 ]
Multiplying each vertex by this matrix gives the new coordinates of the vertices after the rotation:
C'(-8,-2) -> C''(2,-8)
D'(-4,0) -> D''(0,-4)
E'(-1,-6) -> E''(6,1)
F'(-7,-4) -> F''(4,-7)
The trapezoid C'D'E'F' has been rotated 270° counter-clockwise about the origin to a new position C''D''E''F''.
To know more about translation visit:
https://brainly.com/question/29060762
#SPJ1
Find the value of x for which ABCD must be a parallelogram.

Answers
3x-5=2x+3
3x-5+5=2x+3+5
3x=2x+8
3x-2x=2x-2x+8
x=8
x=8
i also need help on this lol please
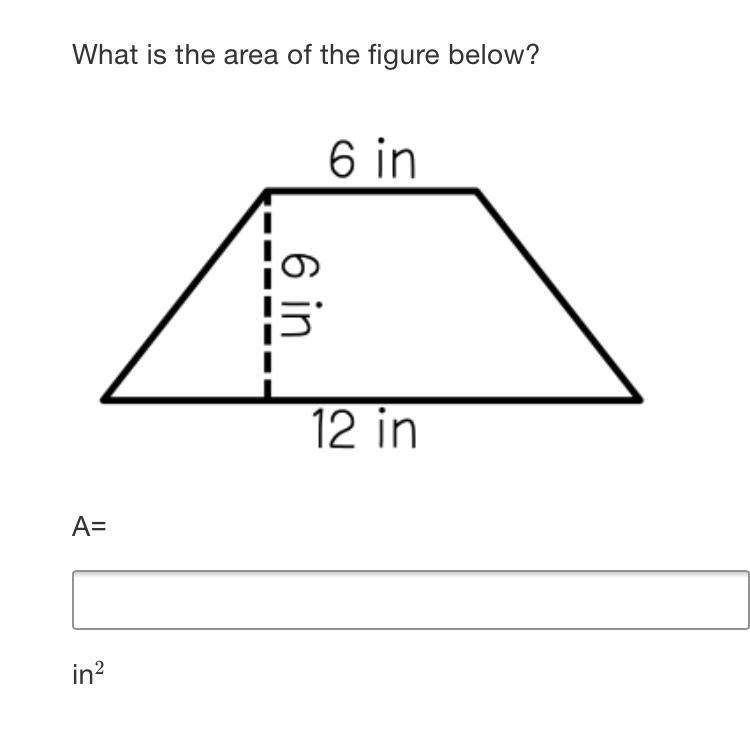
Answers
Plz help!!!!!!!!!!!!!!!!!!!

Answers
Answer:
h(0) = 10
h(4) = 16
Step-by-step explanation:
h(0) = 2(0)² - 3(0) + 10 = 10
h(4) = 2^4 = 16
Identify the zero(s) of \(f(x)=4x^{2} - 20x - 56\). -- Urgent 10 minutes! Many points!
Answers
Answer:
x = - 2, x = 7
Step-by-step explanation:
Given
f(x) = 4x² - 20x - 56
To find the zeros let f(x) = 0, that is
4x² - 20x - 56 = 0 ( divide through by 4 )
x² - 5x - 14 = 0 ← in standard form
(x - 7)(x + 2) = 0 ← in factored form
Equate each factor to zero and solve for x
x + 2 = 0 ⇒ x = - 2
x - 7 = 0 ⇒ x = 7
S(-4, -6) and T(-7, -3); Find R
Answers
Based on the coordinates of S and T and the fact that R is the endpoint, the coordinates of R are (-1, -9).
What are the coordinates of R?S is the midpoint of RT which means that it can be used to find the endpoint of R.
Using the mid-point formula, the value of x for the endpoint R is:
-4 = (x - 7) / 2
-8 = x - 7
x = -1
The value of y for the endpoint R is:
-6 = (y - 3) / 2
-12 = y - 3
y = -9
The endpoint R has coordinates of (-1, -9).
Find out more on the midpoint at https://brainly.com/question/5566419
#SPJ1
Example 4 A closed box has a fixed surface area A and a square base with side x. (a) Find a formula for the volume, V. of the box as a function of x. What is the domain of V? (b) Graph V as a function of x. (c) Find the maximum value of V.
use the work in example 4 in this section of the textbook to find a formula for the volume of a box having surface area 10.
Answers
The volume of the box with surface area 10 is given by the formula V = 2.5x^2 - 0.25x^4, where x is the length of a side of the square base.
To find a formula for the volume of the box with surface area A and square base with side x, we first need to find the height of the box. Since the box has a square base, the area of the base is x^2. The remaining surface area is the sum of the areas of the four sides, each of which is a rectangle with base x and height h. Therefore, the surface area A is given by:
A = x^2 + 4xh
Solving for h, we get:
h = (A - x^2) / 4x
The volume V of the box is given by:
V = x^2 * h
Substituting the expression for h, we get:
V = x^2 * (A - x^2) / 4x
Simplifying, we get:
V = (Ax^2 - x^4) / 4
The domain of V is all non-negative real numbers, since both x^2 and A are non-negative.
To graph V as a function of x, we can use a graphing calculator or plot points using a table of values. The graph will be a parabola opening downwards, with x-intercepts at 0 and sqrt(A) and a maximum at x = sqrt(A) / sqrt(2).
To find the maximum value of V, we can take the derivative of V with respect to x and set it equal to 0:
dV/dx = (2Ax - 4x^3) / 4
Setting this equal to 0 and solving for x, we get:
x = sqrt(A) / sqrt(2)
Plugging this value of x into the formula for V, we get:
V = A^1.5 / (4sqrt(2))
Therefore, the maximum value of V is A^1.5 / (4sqrt(2)).
To find the formula for the volume of a box having surface area 10, we simply replace A with 10 in the formula we derived earlier:
V = (10x^2 - x^4) / 4
Simplifying, we get:
V = 2.5x^2 - 0.25x^4
Therefore, the volume of the box with surface area 10 is given by the formula V = 2.5x^2 - 0.25x^4, where x is the length of a side of the square base. The domain of V is all non-negative real numbers.
Learn more about : General Geometry - https://brainly.com/question/31426425
#SPJ11
pls help its due in 10 minutes

Answers
Answer:
y=9
Step-by-step explanation:
Determine the seating capacity of an auditorium with 30 rows of seats if there are 20 seats in the first row, 24 seats in the second row, 28 seats in the third row, and so on
Answers
Answer:
The seating capacity of the auditorium is 2,340.
Step-by-step explanation:
This question relates to an Arithmetic Progression (AP).
An Arithmetic Progression (AP) is a sequence of numbers in which the differences of every two consecutive numbers or terms are constant or the same.
Therefore, the seating capacity can be calculated using the an arithmetic progression (AP) formula as follows:
Seating capacity = (n / 2) * (2a_1 + (n - 1)d) ...................... (1)
Where;
n = number of rows = 30
a_1 = Number seats in the first row = 20
d = Common difference = 24 - 20 = 28 - 24 = 4
Substituting the values into equation (1), we have:
Seating capacity = (30 / 2) * ((2 * 20) + ((30 - 1) * 4))
Seating capacity = 15 * (40 + (29 * 4))
Seating capacity = 15 * (40 + 116)
Seating capacity = 15 * 156
Seating capacity = 2,340
Therefore, the seating capacity of the auditorium is 2,340.
find the limits
Find the limits. 3 f(x) = 2x² 3x + 3, g(x) = g(x)=√x + 3 (a) lim f(x) = X-2 (b) lim g(x) = (c) lim g(f(x)) X-2 =
Answers
a. The limit is \(\lim_{x \to \ 2} f(x)\) = 13.
b. The limit is \(\lim_{x \to \ 2} g(x)\) = √2 + 3.
c. The limit is \(\lim_{x \to \ 2} g(f(x))\) = g(13).
(a) To find the limit of f(x) as x approaches 2, we substitute the value x = 2 into the expression for f(x):
\(\lim_{x \to \ 2} g(f(x))\) = \(\lim_{x \to \ 2}\) (2x^2 + 3x + 3)
Plugging in x = 2:
\(\lim_{x \to \ 2} f(x)\) = 2(2^2) + 3(2) + 3
= 4 + 6 + 3
= 13
Therefore, \(\lim_{x \to \ 2} f(x)\) = 13.
(b) To find the limit of g(x) as x approaches 2, we substitute the value x = 2 into the expression for g(x):
\(\lim_{x \to \ 2} g(x)\) = \(\lim_{x \to \ 2}\) (√x + 3)
Plugging in x = 2:
\(\lim_{x \to \ 2} g(x)\)= √2 + 3
Therefore, \(\lim_{x \to \ 2} g(x)\) = √2 + 3.
(c) To find the limit of g(f(x)) as x approaches 2, we first find the value of f(x) as x approaches 2:
\(\lim_{x \to \ 2} f(x)\) = 13
Then, we substitute this value into the expression for g(x):
\(\lim_{x \to \ 2} g(f(x))\) = \(\lim_{x \to \ 2}\) g(13)
Since g(13) does not involve x and is a constant, the limit remains the same:
\(\lim_{x \to \ 2} g(f(x))\) = g(13)
Therefore, \(\lim_{x \to \ 2} g(f(x))\) = g(13).
Your full question was
Find the limits. f(x) = 2x² 3x + 3, g(x) = g(x)=√x + 3
(a) \(\lim_{x \to \ 2} f(x)\)
(b) \(\lim_{x \to \ 2} g(x)\)
(c) \(\lim_{x \to \ 2} g(f(x))\)
Learn more about limit at https://brainly.com/question/32527293
#SPJ11
Which is the y-intercept of the line represented by the equation?
4x - 8y = 64
A. (8, 64)
B. (48, -8)
C. (16, 8)
D. (0, -8)
Answers
Answer:
D. (0,-8)
Step-by-step explanation:
Put the equation into slope/y-intercept format:
4x - 8y = 64
-8y = -4x + 64
y = (1/2)x - 8 [The y-intercept is -8; the value of y when x = 0]
D. (0,-8)
I really need help with this please

Answers
Answer:
3x
Step-by-step explanation:
a = 4x - 4
The perimeter is equal to 14x + 8 but it is also equal to 2a + 2b, so
14x + 8 = 2(4x - 4) + 2b
14x + 8 = 8x - 8 + 2b
Let's move 2b to the other side of the equation, we get:
14x + 8 - 2b = 8x - 8
Now, let's move 14x + 8 to the other side too to find what -2b is equal to
-2b = 8x - 14x + 8 - 8
Gonna simplify:
-2b = -6x
Now, let's multiply both sides with -1 to find what 2b is equal to
-2b * -1 = -6x * -1
2b = 6x
Now, we know that 2*b is equal to 6x, but we need to find what side b is equal to, so we gonna divide 6x by two to get what b is equal to
2b = 6x
b = 3x
Side b is equal to 3x
Help me please!!! !!!

Answers
To solve this problem, we need to calculate the volume of water in Container A, the volume of Container B, and subtract the volume of water from Container B from the volume of Container A.
The volume of water in Container A can be found using the formula for the volume of a cylinder:
V = πr^2h
where V is the volume, r is the radius, and h is the height.
For Container A, we have:
V(A) = π(6^2)(15)
V(A) = 1,620π
The volume of Container B can be found using the same formula:
V(B) = π(7^2)(8)
V(B) = 1,232π
After pumping the water from Container A into Container B, Container B is completely full, which means its volume is equal to the volume of the water from Container A.
So, the volume of water in Container A is:
V(water) = V(B)
V(water) = 1,232π
To find the volume of the empty space inside Container A, we need to subtract the volume of water in Container A from the total volume of Container A:
V(empty space) = V(A) - V(water)
V(empty space) = 1,620π - 1,232π
V(empty space) = 388π
V(empty space) ≈ 1,219.8 cubic feet
Therefore, the volume of the empty space inside Container A is approximately 1,219.8 cubic feet (rounded to the nearest tenth of a cubic foot).
Hope you understood it...
Carrie wins 1282 tickets at an arcade for each group of 65 tickets Sheba will receive a prize carry solves the problem 1282÷65 in the terminal is what she has enough tickets right now for 19 prices what is the least number of additional tickets that Carrie needs to win to have enough tickets for the 20th prize
Answers
Answer: 18 tickets.
Step-by-step explanation:
If we compute:
1282/65 = 19.723
So we have enough for 19 prices, and 0.723 for the next one.
Then we must find the next multiple of 65, near 1282.
Now, the easier way to solve this will be:
To have enough for 20 prices, Carrie needs to have at least 20 times 65 tickets.
So she needs:
20*65 = 1300 tickets.
And she has 1282 tickets.
Then the number of tickets that she needs is:
1300 - 1282 = 18 tickets.
She needs 18 more tickets to have enough for the 20th prize.
How do I find the area of this triangle? Please help me this is my second time posting a question I need help ASAP :((

Answers
Answer:
Area = .5 * side 1 * sine (A) * side 2
Area = .5 * 100 * sine (54) * 88
Area = 4,400 * 0.80902
Area = 3,559.688
Step-by-step explanation:

10 points for this!!

Answers
Answer:
1.30 Minutes
2.6 Minutes
3.45 Minutes
Step-by-step explanation:
Answer:
1. 30 minutes
2. 10 minutes
3. 45 minutes
Step-by-step explanation:
1. 60 x .50 = 30
2. 60 x .10 = 10
3. 60 x .75 = 45
the picture above ^^

Answers
Answer:
Step-by-step explanation:
square root of 25x^2 is 5x. square root of 36 is 6
2(5x)(6)
60x
PLEASE HELP! I WILL GIVE BRAINLIEST!
Which expression better represents the amount of money being subtracted?

Answers
Answer:
2.25-1.75=.50
1. Write the distance from the Sun to Mercury in scientific notation. Include units with your answer.
NEED HELP ASAP WILL GIVE BRAINLIST TO BEST AWNSER
Answers
Answer:
3.456 × 10^11
Step-by-step explanation:
= 3.456 × 10^11
scientific notation
= 3.456e11
scientific e notation
= 345.6 × 10^9
engineering notation
billion; prefix giga- (G)
= 3.456 × 10^11
standard form
11
Order of Magnitude
for scientific and standard forms
= 345600000000
(real number)
= three hundred forty-five billion six hundred million
word form
I hope this helps!! :D

BRAINLIEST!!
10 POINTS!! PLZ HELP !!!!
PLEASE ANSWER STEP BY STEP
WILL MARK AS THE BRAINLIEST IF ITS THE CORRECT ANSWER
58.
Find the median of following data :
973, 927, 946, 975, 923, 912,909, 899, 998, 856, 894, 943, 916, 958
Answers
Answer:
910.5
Step-by-step explanation:
Since median is the middle number and there are two of them remaining. You take those two remaining numbers add them then you divide by two.
912+909=1821
=1821÷2
=910.5
Answer:
925
Step-by-step explanation:
You arrange the numbers from the smallest to the largest.
856,894,899,909,912,916,923,927,943,946,958,973,975,998.
Eliminate a number from the starting point and consecutively eliminate from the last point. Do this continuously.
You will be left with 923 and 927.
Add the two numbers then divide by 2.
