Answers
This has to do with the solution the quadratic equation given as: y=x² - 5x -14.
What is the solution and related quantities?
To factorize the quadratic equation - y = x² - 5x -14, we need to find two numbers that multiply to -14 and add up to -5.
We can list out the factors of -14 as follows:
-1 and 14
1 and -14
-2 and 7
2 and -7
Out of these pairs, the numbers that add up to -5 are -2 and 7.
Therefore, we can factorize the equation as:
y = (x - 2)(x + 7)
To find the zeros or x-intercepts, we set each factor equal to 0 and solve for x:
x - 2 = 0, x + 7 = 0
x = 2, x = -7
So the solutions are (2, 0) and (-7, 0).
The axis of symetry is the average of the x-intercepts
This is (2 - 7)/2 = -2.5.
Substituting this value into the equation:
y = (-2.5 )² - 5 (-2.5 ) - 14 = - 20.25
So the vertex is ( -2.5, -20.25).
The domain of the function is all real numbers, since there are no restrictions on the input x.
The range of the function is y ≥ -20.25, since the vertex is the lowest point of the parabola and the graph extends upward from there. See the graph attached.
Learn more about quadratic functions:
https://brainly.com/question/27958964
#SPJ1

Related Questions
How had the New Deal given the government an advantage in preparing for war?
A. The New Deal focused on creating jobs in the weapons industry.
B. Farmers had been encouraged to plant more crops, making more food
C. The government owned a lot of the peoples' debt, and could ask for favors.
D. The government had become closely involved in social and economic affairs
Answers
A store is having a sale on jelly beans and almonds. For 3 pounds of jelly beans and 5 pounds of almonds, the total cost is $27. For 9 pounds of jelly beans and
7 pounds of almonds, the total cost is $51. Find the cost for each pound of jelly beans and each pound of almonds.
Cost for each pound of jelly beans:
Cost for each pound of almonds:
Answers
Answer:
Cost for each pound of jelly beans: $2.75
Cost for each pound of almonds: $3.75
Step-by-step explanation:
Let J be the cost of one pound of jelly beans.
Let A be the cost of one pound of almonds.
Using the given information, we can create a system of equations.
Given 3 pounds of jelly beans and 5 pounds of almonds cost $27:
\(\implies 3J + 5A = 27\)
Given 9 pounds of jelly beans and 7 pounds of almonds cost $51:
\(\implies 9J + 7A = 51\)
Therefore, the system of equations is:
\(\begin{cases}3J+5A=27\\9J+7A=51\end{cases}\)
To solve the system of equations, multiply the first equation by 3 to create a third equation:
\(3J \cdot 3+5A \cdot 3=27 \cdot 3\)
\(9J+15A=81\)
Subtract the second equation from the third equation to eliminate the J term.
\(\begin{array}{crcrcl}&9J & + & 15A & = & 81\\\vphantom{\dfrac12}- & (9J & + & 7A & = & 51)\\\cline{2-6}\vphantom{\dfrac12} &&&8A&=&30\end{array}\)
Solve the equation for A by dividing both sides by 8:
\(\dfrac{8A}{8}=\dfrac{30}{8}\)
\(A=3.75\)
Therefore, the cost of one pound of almonds is $3.75.
Now that we know the cost of one pound of almonds, we can substitute this value into one of the original equations to solve for J.
Using the first equation:
\(3J+5(3.75)=27\)
\(3J+18.75=27\)
\(3J+18.75-18/75=27-18.75\)
\(3J=8.25\)
\(\dfrac{3J}{3}=\dfrac{8.25}{3}\)
\(J=2.75\)
Therefore, the cost of one pound of jelly beans is $2.75.
Let A be a 7×5 matrix with rank equal to 4 and let b be a vector in R8. The four fundamental sub- spaces associated with A are R(A), N(AT ), R(AT ), and N (A).
Answers
The value of R(A) = 4, N(AT ) = 3, R(AT ) = 4, and N (A) = 3.
Given that
Dimension of matrix = 7×5
Rank of matrix = 4
The range space of A,
Which is a subspace of R, is known as R(A).
It is made up of all conceivable linear combinations of A's columns.
The dimension of R(A) = rank of A,
Which is 4 in this case.
The null space of the transpose of A,
Which is also a subspace of R, is designated as N(AT).
All potential answers to the equation ATx = 0,
Where x is a R column vector, are included in it.
N(AT) has a dimension = nullity of A,
which in this case is 3 in this example.
The range space of the transposition of A, is designated as R(AT).
The rows of A are arranged in all conceivable linear configurations.
The rank of A = 4
Thus it equal to dimension of R(AT).
N(A) is the null space of A.
Axe = 0, where x is a column vector in R, are included in it.
The nullity of AT, which is three, is likewise equivalent to the dimension of N(A).
To learn more about matrix visit:
https://brainly.com/question/29132693
#SPJ1
For each equation, decide whether the line it represents is parallel to p, perpendicular to p, or neither.
y=-3x+10
type your answer.....
y-5=-(2+2) type your answer...
type your answer...
-3x+y=1 type your answer.....
Answers
The lines are neither parallel nor perpendicular to line p
Deciding whether the line are parallel or notFrom the question, we have the following parameters that can be used in our computation:
y = -3x + 10
As a general rule
Parallel lines have equal slopesPerpendicular lines have their slopes to be opposite reciprocalsUsing the above as a guide, we have the following:
y - 5 = -(2+2) is neither parallel nor perpendicular to y = -3x + 10-3x + y = 1 is neither parallel nor perpendicular to y = -3x + 10Read more about linear relations at
https://brainly.com/question/30318449
#SPJ1
Find the product of ¾ and 1⅓ a)0 (b)1 (c)12 (d)1⁵/7

Answers
The value of the product of the number as given in the task content is; Choice B; 1.
What is the value big the product of the values; ¾ and 1⅓?It follows from the task content that the numbers whose product are to be determined are; ¾ and 1⅓.
To effectively multiply, we must convert the mixed number to a fraction as follows;
1⅓ = 4/3.
Hence, the product is; 4/3 × 3/4 = 12/12 = 1.
Read more on product of numbers;
https://brainly.com/question/10873737
#SPJ1
Let (1=1,2,3, 4, 5, 6, 7, 8, 9, 10

Answers
The list of elements in the sets are as follows:
A. A ∩ B = {2, 9}
B. B ∩ C = {2, 3}
C. A ∪ B ∪ C = {1, 2, 3, 5, 7, 8, 9, 10}
D. B ∪ C = {2, 3, 5, 7, 9, 10}
How to find the elements in a set?Set are defined as the collection of objects whose elements are fixed and can not be changed.
Therefore,
universal set = U = {1,2,3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 2, 7, 8, 9}
B = {2, 3, 5, 9}
C = {2, 3, 7, 10}
Therefore,
A.
A ∩ B = {2, 9}
B.
B ∩ C = {2, 3}
C.
A ∪ B ∪ C = {1, 2, 3, 5, 7, 8, 9, 10}
D.
B ∪ C = {2, 3, 5, 7, 9, 10}
learn more on set here: https://brainly.com/question/29484130
#SPJ1
How many liters each of a 30% acid solution and a 50 % acid solution must be used to produce 70 liters of a 40 % acid solution? (Round to two decimal places if
necessary.)
Answers
Answer:
30%: 35 liters
50%: 35 liters
Step-by-step explanation:
The desired concentration is halfway between the concentrations of available solutions, so the mixture will be equal amounts of each.
35 liters of 30% acid and 35 liters of 50% acid must be used
_____
If you want to write an equation, it usually works well to let the variable represent the amount of the most concentrated constituent: 50% acid. Then the amount of acid in the final mix is ...
0.50x +0.30(70 -x) = 0.40(70)
0.20x +21 = 28 . . . . simplify
0.20x = 7 . . . . . . . . . subtract 21; next, divide by 0.20
x = 35 . . . . . . amount of 50% solution (liters)
70-x = 35 . . . amount of 30% solution (liters)
Consider a 3 x 3 matrix 0.000 0.000 0.000
A= 3.000 3.000 -3.000
0.000 0.000 0.000 Find three linearly independent eigenvectors 0.000 0.000 0.000 v1, v2, v3 and their eigenvalues λ1, λ2, λ3. In order to be accepted as correct, all entries of the vector Av; λivi must have absolute value smaller than 0.05. Your eigenvalues will only be correct if the corresponding vectors are eigenvectors with these eigenvalues.
v1 = -1 is an eigenvector of A to the eigenvalue λi = 0 1
0
v2 = -1 is an eigenvector of A to the eigenvalue λ2= 0
0
1
v2 = 0 is an eigenvector of A to the eigenvalue λ3= 0
1
0
Answers
As per the matrix, the three linearly independent eigenvectors are 0, 0.05 and 1.
Now let's consider the given matrix A. We are asked to find three linearly independent eigenvectors and their corresponding eigenvalues. Linearly independent eigenvectors are important because they allow us to represent any vector in the space as a linear combination of these eigenvectors.
The first eigenvector v1 is -1, and it corresponds to the eigenvalue λ1 = 0. To check if this is indeed an eigenvector, we multiply it by A and check if the resulting vector is a scalar multiple of v1. In this case, Av1 = 0v1, which means that v1 is indeed an eigenvector with eigenvalue λ1 = 0.
The second eigenvector v2 is also -1, and it corresponds to the eigenvalue λ2 = 0. Again, we multiply it by A and check if the resulting vector is a scalar multiple of v2. Av2 = 0v2, which means that v2 is an eigenvector with eigenvalue λ2 = 0.
The third eigenvector v3 is 0, and it corresponds to the eigenvalue λ3 = 1. We repeat the same process and check if Av3 is a scalar multiple of v3. In this case, Av3 = 0.05v3, which satisfies the given condition of having all entries with absolute value smaller than 0.05. Therefore, v3 is an eigenvector with eigenvalue λ3 = 1.
To know more about matrix here
https://brainly.com/question/28180105
#SPJ4
how many solutions are in -2x+3 = -2x+3
Answers
Answer:
Infinite Solutions
Step-by-step explanation:
If the two equations are the same (as they are here), the amount of solutions would be infinite. I hope this helps!
Jose has saved $135 towards the purchase of a PlayStation 5. The total cost of the PS5 is $499. How much more money does Jose need to save?
Write an addition equation and solve.
Answers
Answer:
Let x be how much more money Jose needs to save.
135 + x = 499
x = 364
Jose needs to save 364 more dollars.
Let me know if this helps!
Answer:
364*
Step-by-step explanation:
499-135=314
364+ 135=499
I put 449 instead of 499 so now i feel foolish. But that's okayy.
Please helpppppppppppppp <3

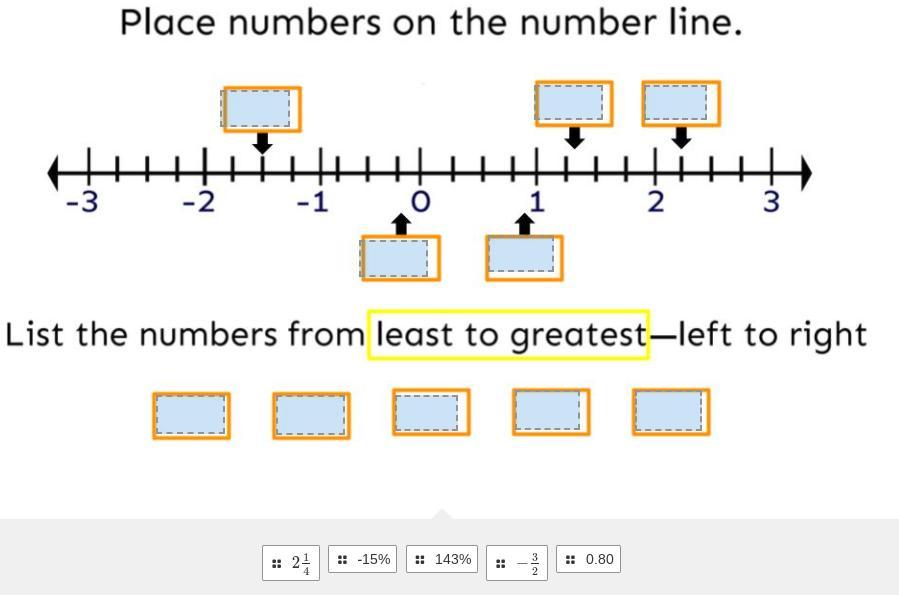
Answers
First attached in this order:
The 1st one
the 3rd one
The 4th one
The 2nd one
Step by-step explanation:
I'll write the answer in the comments for the 2nd attachment.
Answer:
Part 1: -10, -5, 0, 8 Part 2: -3/2, -15%, 0.80, 143%, 2 1/4
Step-by-step explanation:
Part 1: The lower the number, the lower the temperature
Part 2: Convert the fractions into decimals
2 1/4 = 2.25
-15% = -0.15
143% = 1.43
-3/2 = -1.5
0.80 = 0.80
The order from least to greatest is -3/2, -15%, 0.80, 143%, 2 1/4
Hope this helps :)
HII i really need help

Answers
Answer:
when in doubt choose c
Step-by-step explanation:
Answer: 11/48 cubic feet
Step-by-step explanation:
alright ill try my best to explain
so you use the formula V = 22/21r^2h
where V is volume
r is radius
and h is height of cone
you simply plug in the values given in the question, so
V=22/21*1/2^2*7/8
so the answer would be 11/48 cubic feet
Find the indicated function given f(x)=2x^2+1 and g(x)=3x-5Answer in simplified answers in descending powers of x.

Answers
We will have the following:
1. f(g(2)):
\(g(2)=3(2)-5\Rightarrow g(2)=1\)\(\Rightarrow f(g(2))=2(1)^2+1\Rightarrow f(g(2))=3\)2. f(g(x)):
\(f(g(x))=2(3x-5)^2+1\Rightarrow f(g(x))=2(9x^2-30x+25)+1\)\(\Rightarrow f(g(x))=18x^2-60x+51\)3. g(f(x)):
\(g(f(x))=_{}3(2x^2+1)-5\Rightarrow g(f(x))=6x^2-2\)4. (g ° g)(x):
\((g\circ g)(x)=3(3x-5)-5\Rightarrow(g\circ g)(x)=9x-20\)5. (f ° f)(x):
\((f\circ f)(x)=2(2x^2+1)^2+1\Rightarrow(f\circ f)(x)=2(4x^4+4x^2+1)+1\)\(\Rightarrow(f\circ f)(x)=8x^4+8x^2+3\)823× 3.6 weekly math review homework for fifth grade
Answers
BEEN STUCK FOR A WHILE PLEASE HELP!! Find the perimeter and area for the triangle. Be sure to write the formula, and use correct measure.

Answers
Answer:
Area = 77ft²
Perimeter = 44 9/20 feets
Step-by-step explanation:
Area of a triangle = 1/2 * base * height
Base = 19 1/4 feets = 77/4 feets
Height = 8 feets
Area = 1/2 * 77/4 * 8
Area = (77 * 8) / 8
Area = 77 feet²
Perimeter of a triangle :
Sum of the sides
Perimeter = a + b + c
Perimeter = 19 1/4 + 10 + 15 1/5
Perimeter = 44 + (1/4 + 1/5)
Perimeter = 44 9/20
Please help I’m giving brainliest!

Answers
=================================================
Explanation:
Label the center point of the circle as point G.
Also, label the top and bottom tangent points as H and J respectively. This means that H is on line segment ED, while J is on line segment EF.
The given arc measure of 100 degrees directly leads to the central angle HGJ to be 100 degrees.
Focus on quadrilateral EHGJ. It has two right angles at points H and J since they are tangent points. Angle G of this quadrilateral was found to be 100. Let's find angle E
E+H+G+J = 360 ..... any four angles of a quadrilateral add to 360
E+90+100+90 = 360
E+280 = 360
E = 360-280
E = 80
Or as a shortcut, we can note that angles E and G must add to 180, since H+J = 90+90 = 180, making up half of 360.
So, E+G = 180 leads to E+100 = 180 which solves to E = 80.
Once we know that E = 80, this leads to angle DEF to be 80 degrees.
This is an inscribed angle that subtends arc DF. By the inscribed angle theorem, we double the inscribed angle value to get the arc measure
arc DF = 2*(inscribed angle DEF)
arc DF = 2*(80)
arc DF = 160 degrees
What is the justification for step 1 in the solution process?
-22 - x = 14 + 6x
Answers
Answer:
addition property of equality
Step-by-step explanation:
You want the justification for step 1 in the solution process for -22 - x = 14 + 6x.
SolutionNo solution process steps are shown, but we can speculate what they might be.
The goal is to separate constant terms and variable terms. This can be done several ways, but generally consists of adding the same thing to both sides of the equation.
Often, you're told to collect the variable terms first. Some prefer to do that so the variable terms are on the left side of the equal sign. Others prefer to do that so the result has a positive coefficient for the variable term. Taking the latter tack, we want to add x (the opposite of -x) to both sides of the equation:
-22 -x +x = 14 +6x +x . . . . . x added to both sides
-22 = 14 +7x . . . . . . . simplified
The justification for this step is the addition property of equality. That property allows you to add the same thing to both sides of an equation without changing the values of the variables.
__
Additional comment
Step 2 would be to add -14 to both sides, giving you ...
-36 = 7x . . . . . . . . add -14; addition property of equality
If you like, you can do both of these additions in one step:
-22 -x +(x -14) = 14 +6x +(x -14) . . . add(x -14); addition property of equality
-36 = 7x . . . . . . simplified
Step 3 is to divide by the coefficient of the variable.
-36/7 = (7x)/7 . . . . division property of equality
-5 1/7 = x . . . . . . . simplified. This is the solution.
The usual procedure takes 3 steps, so this is called a "3-step equation."
Note that we choose for the variable coefficient to be positive, because we judge arithmetic with positive numbers to be less error-prone. If you collect the variable terms on the left, you get ...
-7x = 36
so have to divide by -7. This should not be an issue if you're careful with your arithmetic, but many find dealing with negative numbers to be a challenge.
4. The value of (1+2+3+...+20) is 210. What is the value of (3+6+9+...+57)?
B) 630
A) 627
C) 570
D) 573
E) 580
Answers
By using sum of sequence the value of (3+6+9+...+57) is 570, which is option C).
What is sum of the sequence ?
The sum of a sequence is the total result of adding up all the numbers in the sequence. The method for finding the sum of a sequence depends on whether the sequence is arithmetic or geometric.
For an arithmetic sequence, in which each term is obtained by adding a fixed number (called the common difference) to the previous term, the sum of the first n terms can be found using the formula:
\(Sn = n/2(2a + (n-1)d)\)
where a is the first term, d is the common difference, and n is the number of terms.
For a geometric sequence, in which each term is obtained by multiplying the previous term by a fixed number (called the common ratio), the sum of the first n terms can be found using the formula:
\(Sn = a(1-r^n) / (1-r)\)
where a is the first term, r is the common ratio, and n is the number of terms.
According to the question:
We can notice that each number in the sequence 3, 6, 9, ..., 57 is 3 times the corresponding number in the sequence 1, 2, 3, ..., 19.
So, we can find the sum of the sequence 3, 6, 9, ..., 57 by finding the sum of the sequence 1, 2, 3, ..., 19 and then multiplying by 3.
The sum of the sequence 1, 2, 3, ..., 19 is:
1 + 2 + 3 + ... + 19 = (19/2)(1 + 19)/2 = 190
Multiplying by 3, we get:
3 + 6 + 9 + ... + 57 = 3(1 + 2 + 3 + ... + 19) = 3(190) = 570
Therefore, the value of (3+6+9+...+57) is 570, which is option C).
To know more about sum of sequence visit:
https://brainly.com/question/28812249
#SPJ1
Find the volume of the following figure

Answers
so it would be 6 x 4 x 2 so the answer is 48
Write this trinomial in factored form.
7x^2 - 16x - 15
Enter the correct answer.
Answers
Hey there! :)
Answer:
(7x +5)(x - 3)
Step-by-step explanation:
Starting with:
7x² - 16 - 15
Find two numbers that add up to -16 and multiply to form -15. Remember the coefficient of 7 in the front of the equation.
The numbers '5' and '-3' can be derived. Put these into factored form:
(7x +5)(x - 3)
A shipping container is in the shape of a right rectangular prism with a length of 2.5
feet, a width of 13 feet, and a height of 11 feet. The container is completely filled with
contents that weigh, on average, 0.55 pound per cubic foot. What is the weight of the
contents in the container, to the nearest pound?

Answers
9514 1404 393
Answer:
197 pounds
Step-by-step explanation:
To find the total weight, we can multiply the weight of each cubic foot by the number of them. The number of cubic feet is found using the volume formula ...
V = LWH
V = (2.5 ft)(13 ft)(11 ft) = 357.5 ft³
Then the total weight of the contents is ...
(357.5 ft³)(0.55 lb/ft³) = 196.625 lb
The weight of the contents is about 197 pounds.
(6-2x) +(15-3x) where x=0.2
Answers
\( \sf{\blue{«} \: \pink{ \large{ \underline{A\orange{N} \red{S} \green{W} \purple{E} \pink{{R}}}}}}\)
Expression: \(\displaystyle\sf (6-2x) +(15-3x)\)
Substituting \(\displaystyle\sf x=0.2\):
\(\displaystyle\sf (6-2(0.2)) +(15-3(0.2))\)
Simplifying the expression inside the parentheses:
\(\displaystyle\sf (6-0.4) +(15-0.6)\)
\(\displaystyle\sf 5.6 +14.4\)
Calculating the sum:
\(\displaystyle\sf 20\)
Therefore, \(\displaystyle\sf (6-2x) +(15-3x)\) evaluated at \(\displaystyle\sf x=0.2\) is equal to \(\displaystyle\sf 20\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
solve for x
(look at photo)

Answers
By definition of proportion, the value of x is,
⇒ x = 80
We have to given that;
In a triangle,
Perpendicular = 60
Now, By Pythagoras theorem we get;
60² = 36² + y²
3600 = 1296 + y²
y² = 3600 - 1296
y² = 2304
y = 48
Hence, By definition of proportion;
⇒ x / 48 = 60 / 36
⇒ x = 80
Thus, By definition of proportion, the value of x is,
⇒ x = 80
Learn more about the proportion visit:
https://brainly.com/question/1496357
#SPJ1
if the mean of a data is 316 and the sum of its observation is 3792 find the number of observations in the data.
Answers
Answer:
12
Step-by-step explanation:
mean is calculated as
mean = \(\frac{sum}{count}\)
Here mean = 316 and sum = 3792 , count n is required to be found, so
\(\frac{3792}{n}\) = 316 ( multiply both sides by n )
3792 = 316n ( divide both sides by 316 )
12 = n
There are 12 observations in the data
Find an equation of the tangent plane to the given parametric surface at the specified point. I and the tangent plane. r(u,v)=u cos v hat xi +u sin y dot y +vk ; u = 5 v = pi / 3
Answers
The equation of tangent plane to the given parametric surface \(r(u,v) = u.cos(v)i + u.sin(v)j + vk\) is \(\frac{\sqrt3}{2}x - \frac{5}{2}y + 5z = \frac{5\pi}{3}\) .
The given parametric surface is
\(r(u,v) = u.cos(v)i + u.sin(v)j + vk\)
The tangent vectors are
⇒ \(r_u = \frac{dx}{du} i+ \frac{dy}{du}j + \frac{dz}{du}k\)
⇒ \(r_u =\) \(r(u,v) = cos(v)i + sin(v)j + 0k\)
⇒ \(r_v = \frac{dx}{dv} i+ \frac{dy}{dv} j+ \frac{dz}{dv} k\)
⇒ \(r_v =\) \(r(u,v) = -u.sin(v)i + u.cos(v)j + 1k\)
The normal vector to the tangent plane is
\(r_u r_v = \left[\begin{array}{ccc}i&j&k\\cos(v)&sin(v)&0\\-usin(v)&ucos(v)&1\end{array}\right]\)
⇒ \(r_u r_v =\) \(sin(v)i - cos(v)j + u.k\)
When u = 5, v = \(\frac{\pi }{3}\), the normal vector becomes
⇒ \(sin(\frac{\pi}{3})i - cos( \frac{\pi}{3})j + k\)
⇒ \(\frac{\sqrt{3} }{2}i - \frac{1}{2} j + k\)
The point on the surface corresponding to the u = 5 & v= \(\frac{\pi}{3}\) is
\(r(5, \frac{\pi}{3}) = (5)cos(\frac{\pi}{3})i + (5)sin(\frac{\pi}{3})j + (\frac{\pi}{3})k\\r(5, \frac{\pi}{3}) = \frac{5}{2}i + \frac{5\sqrt3}{2}j + \frac{\pi}{3}k\)
If a is the position vector of a point on the plane & n is a vector normal to the plane, then the equation of the plane is
⇒ (r - a).n = 0
⇒ \((x - \frac{5}{2}) . ( \frac{5\sqrt3}{2}) + (y - \frac{5\sqrt3}{2}).(- \frac{5}{2}) + (z - \frac{\pi}{3}).(5) = 0\)
⇒ \(\frac{\sqrt3}{2}x - \frac{5}{2}y + 5z = \frac{5\pi}{3}\)
To learn more about parametric forms
https://brainly.com/question/29146759
#SPJ4
What is the complementary angle of CFB

Answers
Step-by-step explanation:
CFB reads as twenty five degrees
complementary angle will add to it to sum 90 degrees = sixty five degrees
angle CFD is sixty five degrees
EspanolAvicenna, a major insurance company, offers five-year life insurance policies to 65-year-olds. If the holder of one of these policiesdies before the age of 70, the company must pay out $27,400 to the beneficiary of the policy. Executives at Avicenna areconsidering offering these policies for $765 each. Suppose that for each holder of a policy there is a 3% chance that they will diebefore the age of 70 and a 97% chance they will live to the age of 70.00If the executives at Avicenna know that they will sell many of these policies, should they expectto make or lose money from offering them? How much?To answer, take into account the price of the policy and the expected value of the amount paldout to the beneficiary.Avicenna can expect to make money from offering these policies.In the long run, they should expect to make dollars on each policy sold.Avicenna can expect to lose money from offering these policies,

Answers
Answer:
Avicenna can expect to lose money from offering these policies. In the long run, they should expect to lose 57 dollars on each policy sold.
Explanation:
If a person lives to the age of 70, they will earn $765. So, there is a 97% chance to earn $765. On the other hand, if a person dies before age of 70, they will lose $26635 because
$27,400 - $765 = 26,635
Then, there is a 3% chance to lose $26635.
Now, we can find the expected value, multiplyion each option by its probability, so:
E = $765(0.97) - (26635)(0.03)
E = $742.05 - $799.05
E = - $57
Since the sign is negative they can expect to lose money, so the answer is:
Avicenna can expect to lose money from offering these policies. In the long run, they should expect to lose 57 dollars on each policy sold.
Jessica needs to rent a moving truck for one day. She can choose to rent a moving truck from Rentals Plus or from Speedy Move. At Rentals Plus, it costs $5.24 to rent a moving truck for one day, plus $4.46 per mile driven. At Speedy Move, it costs $85.24 to rent a moving truck for one day, plus $0.46 per mile driven. How many miles would Jessica have to drive for the cost to rent a moving truck for one day to be the same at Rentals Plus and Speedy Move?
Answers
Jessica would have to drive 20 miles for the cost to rent a moving truck for one day to be the same at Rentals Plus and Speedy Move.
How find how many miles would Jessica have to driveLet's assume the number of miles driven is represented by 'm'. The cost of renting a moving truck for one day at Rentals Plus can be calculated using the equation:
Cost at Rentals Plus = $5.24 + $4.46 * m
Similarly, the cost of renting a moving truck for one day at Speedy Move can be calculated using the equation:
Cost at Speedy Move = $85.24 + $0.46 * m
To find the number of miles that makes the costs equal, we can set up the equation:
$5.24 + $4.46 * m = $85.24 + $0.46 * m
By rearranging the equation, we can solve for 'm':
$4.46 * m - $0.46 * m = $85.24 - $5.24
$4 * m = $80
m = $80 / $4
m = 20
Therefore, Jessica would have to drive 20 miles for the cost to rent a moving truck for one day to be the same at Rentals Plus and Speedy Move.
Learn more about cost at https://brainly.com/question/29509552
#SPJ1
A coin is tossed twice in succession. Let A be the event that the first toss is heads and let B the event that the second toss is heads. Find: (a) P(A) (b) P(B) (c) P(A∩B) (d) P(B /A)
Answers
Answer:
Step-by-step explanation:
A coin has two faces, a head (H) or tail (T). Tossing a coin twice in succession would give the following sample size;
{HH, HT, TH, TT}
Given that: A = first toss is heads, B = second toss is heads, then:
i. P(A) = {HH, HT} = 2
ii. P(B) = {TH} = 1
iii. P(A∩B) = {HH} = 1
iv. P(B /A) = \(\frac{1}{2}\)
Simplify the ratio 25 :15
Answers
Answer:
5/3
Step-by-step explanation:
Find the GCD (or HCF) of numerator and denominator
GCD of 25 and 15 is 5
Divide both the numerator and denominator by the GCD
25 ÷ 5
15 ÷ 5
Reduced fraction:
5
3
Therefore, 25/15 simplified to lowest terms is 5/3.
brailiest pls hope it helps
