Answers
Answer:
10
Step-by-step explanation:
The y intercept is when the slope crosses the y axis of the graph, we can find this by looking for the value at x=0. From the graph we can see that y=10 at x=0.
The y-intercept is the point in which the line passes through the y-axis :)
Related Questions
find the 3 × 3 matrix that that rotates a point in r 2 60 degrees about the point (6, 8) (using homogeneous coordinates).
Answers
The 3x3 matrix that rotates a point in R2 60 degrees about the point (6,8) using homogeneous coordinates is:
```
| 1/2 -sqrt(3)/2 6 - 6/2*sqrt(3)|
|sqrt(3)/2 1/2 8 - 6sqrt(3)/2|
| 0 0 1 |
```
To rotate a point in R2 by 60 degrees about the point (6,8), we can use homogeneous coordinates and a 3x3 transformation matrix. The transformation matrix can be constructed as follows:
1. Translate the point (6,8) to the origin by subtracting (6,8) from the point.
2. Rotate the point by 60 degrees counterclockwise around the origin.
3. Translate the point back to its original position by adding (6,8) to the rotated point.
Step 1: Translation matrix
To translate the point (6,8) to the origin, we need to subtract (6,8) from the point. This can be done using the following translation matrix:
```
T = |1 0 -6|
|0 1 -8|
|0 0 1|
```
Step 2: Rotation matrix
To rotate the point by 60 degrees, we need to use the following rotation matrix:
```
R = |cos(60) -sin(60) 0|
|sin(60) cos(60) 0|
| 0 0 1|
```
Note that we are using radians for the angle in the cosine and sine functions, so cos(60) = 1/2 and sin(60) = sqrt(3)/2.
Step 3: Translation matrix
To translate the point back to its original position, we need to add (6,8) to the rotated point. This can be done using the following translation matrix:
```
T' = |1 0 6|
|0 1 8|
|0 0 1|
```
Combining the matrices
To combine the matrices, we can multiply them in the following order: T' * R * T. This gives us the final transformation matrix:
```
M = | 1/2 -sqrt(3)/2 6 - 6/2*sqrt(3)|
|sqrt(3)/2 1/2 8 - 6sqrt(3)/2|
| 0 0 1 |
```
Therefore, the 3x3 matrix that rotates a point in R2 60 degrees about the point (6,8) using homogeneous coordinates is:
```
| 1/2 -sqrt(3)/2 6 - 6/2*sqrt(3)|
|sqrt(3)/2 1/2 8 - 6sqrt(3)/2|
| 0 0 1 |
```
Note that the matrix has been simplified to express the trigonometric functions in terms of radicals.
Visit to know more about Matrix:-
brainly.com/question/94574
#SPJ11
twelve different video games showing drug use were observed. the duration times of drug use were recorded, with the times (seconds) listed below. what requirements must be satisfied to test the claim that the sample is from a population with a mean greater than 80 sec? are the requirements all satisfied?
Answers
The requirements for a one-sample t-test are generally satisfied assuming a simple random sample and a large enough sample size. However, we cannot determine if the normality requirement is met without examining the data.
To test the claim that the sample is from a population with a mean greater than 80 sec, we need to perform a one-sample t-test. The following requirements must be satisfied to use the one-sample t-test:
The sample must be a simple random sample from the population.
The variable under study must be continuous or approximately continuous.
The population must be normally distributed or the sample size should be large (n > 30).
To determine if the requirements are satisfied for the given data, we need to check if the sample is a simple random sample, the variable (duration times of drug use) is continuous or approximately continuous, and if the population is normally distributed or the sample size is large enough.
Assuming that the sample is a simple random sample, we can check the other requirements:
Continuity: The variable (duration times of drug use) is continuous.
Normality: We can examine a histogram, a normal probability plot, or conduct a normality test such as the Shapiro-Wilk test. If the data is approximately normally distributed, we can proceed with the t-test. If not, we can use a non-parametric test.
Without the data, we cannot determine if the normality requirement is met. However, if the sample size is large (n > 30), we can use the central limit theorem to assume normality. In that case, we can proceed with the t-test.
Therefore, the requirements for a one-sample t-test are generally satisfied assuming a simple random sample and a large enough sample size. However, we cannot determine if the normality requirement is met without examining the data.
To learn more about population visit: https://brainly.com/question/27991860
#SPJ11
Jenny baked a circular cake with a diameter of 9 inches and a height of 5 inches. She cuts the cake into 16 equal slices. What is the approximate volume of each slice of cake
Answers
The required answer is approximate volume of each slice of cake is 19.9 cubic inches.
Explanation:-
To find the approximate volume of each slice of cake, follow these steps:
1. Determine the radius of the cake: Since the diameter is 9 inches, the radius is half of that, which is 4.5 inches.
2. Calculate the volume of the entire cake using the formula for the volume of a cylinder: V = πr^2h. In this case, r = 4.5 inches and h = 5 inches.
V = π(4.5)^2(5) ≈ 318.47 cubic inches.
3. Divide the total volume by the number of slices to find the volume of each slice: 318.47 cubic inches / 16 slices ≈ 19.9 cubic inches.
approximate volume of each slice of cake, first calculate the total volume of the cake. We can use the formula for the volume of a cylinder, which is V = πr^2h, where r is the radius (half the diameter) and h is the height. So, the radius of the cake is 4.5 inches (half of 9 inches), and the height is 5 inches. V = π(4.5)^2(5) V ≈ 318 cubic inches Since the cake is cut into 16 equal slices, we can divide the total volume by 16 to get the approximate volume of each slice: 318/16 ≈ 19.9 cubic inches Therefore, the approximate volume of each slice of cake is about 19.9 cubic inches
So, the approximate volume of each slice of cake is 19.9 cubic inches.
To know about volume of cylinder .click the link
https://brainly.com/question/16788902
#SPJ11
An ice cube tray has two rows of 8 cubes in each. How many ice cubes are in a stack of 12 ice cube trays? Draw a picture to explain your reasoning.
Answers
Answer:
The answer is 192
Step-by-step explanation:
add 16 and 16 and keep doing that till you reach 192
Answer:
192
Step-by-step explanation:
how many paving stones each measuring 2.5 m by 2 m be required to pave a rectangular piece of ground 30 metres by 16.5 m?
Answers
Answer:
39 stones
Step-by-step explanation:
find area of each
paving stone: 2.5*2=5
ground: 30*6.5=195
195/5=39
Reduce the third order ordinary differential equation y-y"-4y +4y=0 in the companion system of linear equations and hence solve Completely. [20 marks]
Answers
To reduce the third-order ordinary differential equation y - y" - 4y + 4y = 0 into a companion system of linear equations, we introduce new variables u and v:
Let u = y,
v = y',
w = y".
Taking the derivatives of u, v, and w with respect to the independent variable (let's denote it as x), we have:
du/dx = y' = v,
dv/dx = y" = w,
dw/dx = y"'.
Now we can rewrite the given differential equation in terms of u, v, and w:
u - w - 4u + 4u = 0.
Simplifying the equation, we get:
-3u - w = 0.
This equation can be expressed as a system of first-order linear differential equations as follows:
du/dx = v,
dv/dx = w,
dw/dx = -3u - w.
Now we have a companion system of linear equations:
du/dx = v,
dv/dx = w,
dw/dx = -3u - w.
To solve this system completely, we need to find the solutions for u, v, and w. By solving the system of differential equations, we can obtain the solutions for u(x), v(x), and w(x), which will correspond to the solutions for y(x), y'(x), and y"(x), respectively.
The exact solutions for this system of differential equations depend on the initial conditions or boundary conditions that are given. By applying appropriate initial conditions, we can determine the specific solution to the system.
To learn more about derivatives : brainly.com/question/25324584
#SPJ11
is 8.421 greater than 5.4
Answers
Answer:
YesStep-by-step explanation:
8.421 is greater than 5.4 because...
8.421 - 5.4 = 3.021
If the number was a negative when
you would subtract it, then it would
be less than the other number.
Since it's a positive number, the
number is greater than 5.4
Hope this helps! <3
fond the value of x and find the length of xy

Answers
From this Triangle
Taking Triangle XZH, wanting to find HZ
\(\begin{gathered} We\text{ have to make use of pythgoras Theorem} \\ (XZ)^2=(XH)^2+(HZ)^2 \\ 12^2=8^2\text{ + }(HZ)^2 \\ 144\text{ = 64 + }(HZ)^2 \\ 144-64\text{ = }(HZ)^2 \\ (HZ)^2\text{ = 80} \\ (HZ)\text{ = }\sqrt[]{80\text{ }}\text{ =8.94} \\ \end{gathered}\)From the Second triangle, ZHY
\(\begin{gathered} ZY^2=HZ^2+HY^2 \\ (x+3)^2\text{ =}8.94^2+x^2 \\ x^2+6x^{}\text{ + 9 = }80+x^2 \\ x^2-x^2\text{ + 6x = 80 -9} \\ 6x\text{ = 71} \\ x\text{ =}\frac{71}{6}\text{ =11.83} \\ \end{gathered}\)XY = x + 8
= 11.83 + 8
=19.83

1) Expand the following expressions
(a) 2(x + 6)
Answers
Answer:
2x + (2 × 6)
since we are expanding, we represent 2 multiplying to every expression in the given parentheses
Answer:
2x+12
Step-by-step explanation:
2(x + 6)
Distribute
2*x + 2*6
2x+12
help please! it’s Geometry
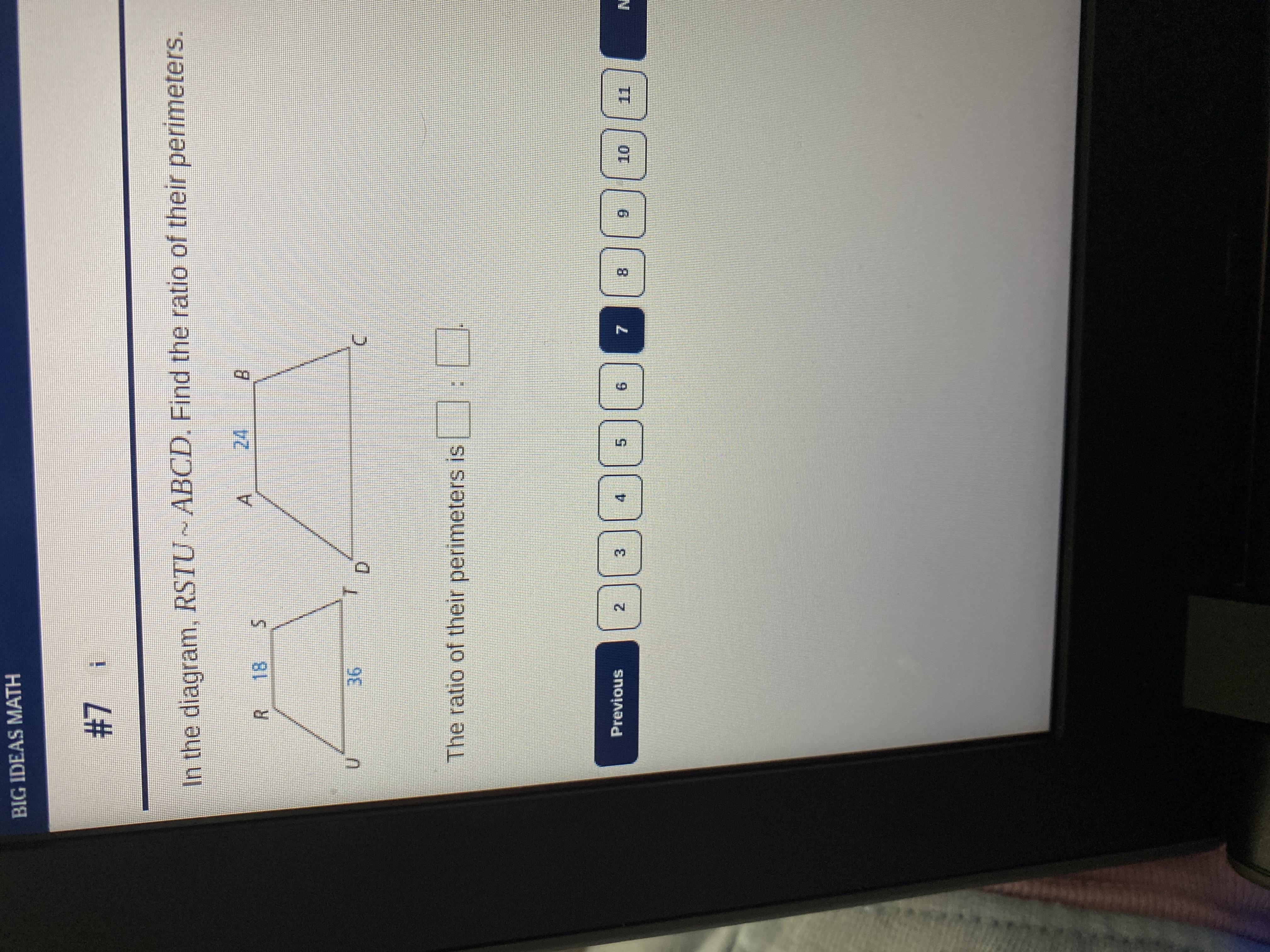
Answers
S=26.32 E=55 t=3 standard diviation=60% 3-year r=2.4% 10-year
r=3.1%
What minimum value would you assign? What isthe maximum value
you would assign?
Answers
For the given standard deviation the minimum value we would assign is 22.the maximum value we would assign is 88.
To calculate the minimum and maximum values based on the given information, we need to consider the standard deviation and the respective interest rates for the 3-year and 10-year periods.
Given:
S = 26.32 (Initial value)
E = 55 (Expected value)
t = 3 (Years)
Standard deviation = 60% (of the expected value)
3-year interest rate = 2.4%
10-year interest rate = 3.1%
To find the minimum value, we will calculate the value at the end of the 3-year period using the lowest possible growth rate.
Minimum value calculation:
Minimum value = E - (Standard deviation * E) = 55 - (0.6 * 55) = 55 - 33 = 22
Therefore, the minimum value we would assign is 22.
To find the maximum value, we will calculate the value at the end of the 10-year period using the highest possible growth rate.
Maximum value calculation:
Maximum value = E + (Standard deviation * E) = 55 + (0.6 * 55) = 55 + 33 = 88
Therefore, the maximum value we would assign is 88.
For more details about standard deviation
https://brainly.com/question/13498201
#SPJ4
The data in the table below shows the average temperature in Northern Latitudes:
The line of best fit for the data is approximately y=-1.07x+92.87.
a) True
b) False

Answers
The line of best fit for the data is approximately y = -1.07x + 92.87: A) True.
How to find an equation of the line of best fit for the data?In order to determine a linear equation for the line of best fit that models the data points contained in the table, we would have to use a graphing calculator (scatter plot).
In this scenario, the latitude would be plotted on the x-axis of the scatter plot while the average temperature would be plotted on the y-axis of the scatter plot.
On the Excel worksheet, you should right click on any data point on the scatter plot, select format trend line, and then tick the box to display an equation for the line of best fit on the scatter plot.
From the scatter plot (see attachment) which models the relationship between the latitude and average temperature, a linear equation for the line of best fit is given by:
y = -1.07x + 92.87
Read more on scatter plot here: brainly.com/question/28605735
#SPJ1

discuss any two advantages of superposition theorem
compared to other circuit theorms
Answers
The advantages of the superposition theorem compared to other circuit theorems are its simplicity and modularity in circuit analysis, as well as its applicability to linear circuits.
Superposition theorem is a powerful tool in circuit analysis that allows us to simplify complex circuits and analyze them in a more systematic manner. When compared to other circuit theorems, such as Ohm's Law or Kirchhoff's laws, the superposition theorem offers several advantages. Here are two key advantages of the superposition theorem:
Simplicity and Modularity: One major advantage of the superposition theorem is its simplicity and modular approach to circuit analysis. The theorem states that in a linear circuit with multiple independent sources, the response (current or voltage) across any component can be determined by considering each source individually while the other sources are turned off. This approach allows us to break down complex circuits into simpler sub-circuits and analyze them independently. By solving these individual sub-circuits and then superposing the results, we can determine the overall response of the circuit. This modular nature of the superposition theorem simplifies the analysis process, making it easier to understand and apply.
Applicability to Linear Circuits: Another advantage of the superposition theorem is its applicability to linear circuits. The theorem holds true for circuits that follow the principles of linearity, which means that the circuit components (resistors, capacitors, inductors, etc.) behave proportionally to the applied voltage or current. Linearity is a fundamental characteristic of many practical circuits, making the superposition theorem widely applicable in real-world scenarios. This advantage distinguishes the superposition theorem from other circuit theorems that may have limitations or restrictions on their application, depending on the circuit's characteristics.
It's important to note that the superposition theorem has its limitations as well. It assumes linearity and works only with independent sources, neglecting any nonlinear or dependent sources present in the circuit. Additionally, the superposition theorem can become time-consuming when dealing with a large number of sources. Despite these limitations, the advantages of simplicity and applicability to linear circuits make the superposition theorem a valuable tool in circuit analysis.
To learn more about superposition theorem visit : https://brainly.com/question/25329462
#SPJ11
Helppp find the slope of the line

Answers
Answer:
2
Step-by-step explanation:
change in y ÷ change in x
4÷2=2
Help please calculate the scale factor of ∆DEF to ∆ABC

Answers

The graph of y = 3^x is shown . What is the value of x when y=27
a . 2
b. 3
c. 9
d. 24
Answers
ABCD is a square.
Need help ASAP.
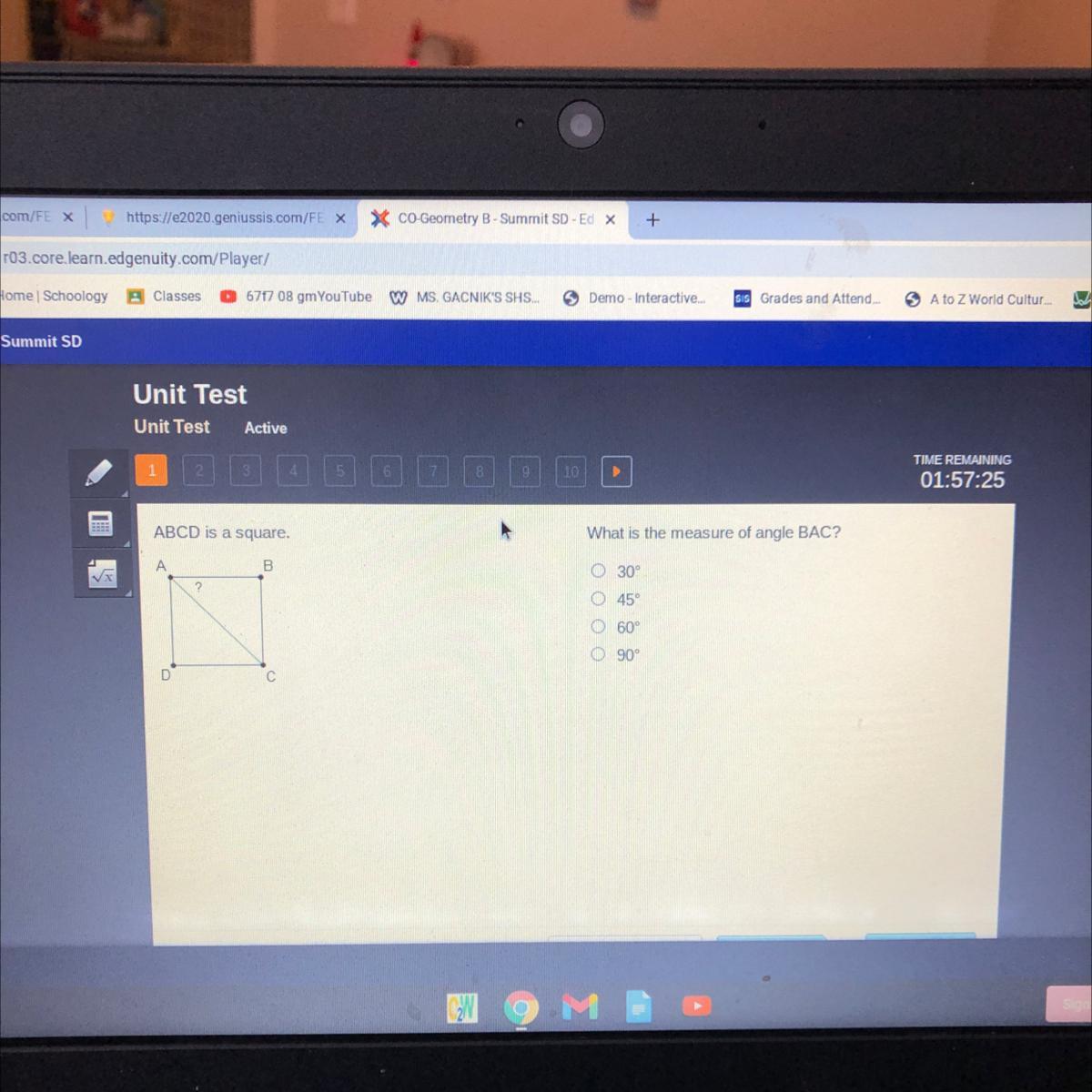
Answers
Can someone please help m with this

Answers
Answer:
Step-by-step explanation:
I take it that what you are asking is which one of the three choices gives f(5) = 2.
It is not the table. When you try adding 5 in the x column, you get a much larger result than 2 for y.
And it is not the scattered points of the graph. x = 5 gives 5 on the y axis, not 2.
It is the first choice on the left.
f(5) = x - 3
f(5) = 5 - 3
f(5) = 2
1. Determine whether the stress function = 50x² - 60xy - 70y² satisfies the conditions of compatibility for a two-dimensional problem. Obtain the stress distribution in the matrix plate. Also draw a sketch showing the boundary stresses on (tensor) form. [4+4+2 points]
Answers
The stress function satisfies the conditions of compatibility for a two-dimensional problem.
Given stress function is 50x² - 60xy - 70y²
To determine whether the stress function satisfies the conditions of compatibility for a two-dimensional problem, it is required to find the strains and then check for compatibility equations.
Strain components are given as,
εx = ∂υ/∂x + (du/dx)
εy = ∂υ/∂y + (du/dy)
γxy = ∂υ/∂y + (du/dx)
Here,
υ = 50x² - 60xy - 70y²
du/dx = 100x - 60
ydu/dy = -60x - 140y
∂υ/∂x = 100x - 60y
∂υ/∂y = -60x - 140y
∂²υ/∂y² = -140
∂²υ/∂x² = 100
Now,εx = 100x - 60
yεy = -140y - 60
xγxy = -60y - 60x
Taking derivative of εy w.r.t x,
∂(εy)/∂x = -60
Similarly, taking derivative of εx w.r.t y,
∂(εx)/∂y = -60
∴ The stress function satisfies the conditions of compatibility for a two-dimensional problem.
Stress components are given as,
σx = (C11εx + C12εy)
σy = (C21εx + C22εy)
τxy = (C44γxy)
Here,C11 = C22 = 100, C12 = C21 = -60 and C44 = 0
Therefore,
σx = 100(100x - 60y) - 60(-140y - 60x)
= 19600x - 8800
yσy = -60(100x - 60y) + 100(-140y - 60x)
= -19600y + 8800x
τxy = 0
To know more about stress visit:
https://brainly.com/question/31366817
#SPJ11
Evaluate the expression when a= 1/4 and b = 6.
16a2 – 4b=
Answers
Step-by-step explanation:
HERE,
a=\(\bold{\dfrac{1}{4} }\)
b=6
so,
According to the question,
\(\bold{16a^2-4b }\)
\(\bold{16\times(\dfrac{1}{4})^2-4\times 6 }\)
\(\bold{ 16\times \dfrac{1}{16}-24 }\)
\(\bold{\cancel{16}\times \dfrac{1}{\cancel{16}}-24 }\)
\(\bold{1-24 }\)
\(\bold{ -23 }\)
find the value of given expression
\( \sqrt{25 \times 625 \times \times 25} \)
Answers
Answer:
±625
Step-by-step explanation:
\(\sqrt{25 x 625 x 25}\)
\(\sqrt{390625}\)
±625
Answer:
√(25×625×25)√{5²×25²×5²)=±(5×25×5}=±625 is your answer
What is the point-slope equation of a line if the slope is 3 and it passes through the point (-9, 2
Answers
Answer:
The point-slope equation of the line is y - 2 = 3(x + 9)
Step-by-step explanation:
The form of the point-slope equation is y - y1 = m(x - x1), where
m is the slope of the line(x1, y1) is a point on the line∵ The slope of a line is 3
∴ m = 3
∵ The line passes through point (-9, 2)
∵ x1 = -9
∴ y1 = 2
→ Substitute the values of m, x1, and y1 in the point-slope form
∵ y - y1 = m(x - x1)
∴ y - 2 = 3(x - (-9))
→ Remember (-)(-) = (+)
∴ y - 2 = 3(x + 9)
∴ The point-slope equation of the line is y - 2 = 3(x + 9)
Answer this problem

Answers
Answer:
(3,-7)
(-8,48)
(-4,28)
(8,-32)
(-3,23)
Step-by-step explanation:
To solve, just put in the x value from the table as the x value in the equation. Then solve to get y.
Hope it helps!
During the month of march, hazure services made purchases on account totaling $43,500. Also during the month of march, hazure was paid $8,000 by a customer for services to be provided in the future and paid $36,900 of cash on its accounts payable balance. If the balance in the accounts payable account at the beginning of march was $77,300, what is the balance in accounts payable at the end of march?.
Answers
The balance of Accounts Payable at the end of March is $83,900.
According to question;
Balance in the beginning Accounts payable account =$77,300
Add: Purchases made during the month on account = $43,500
Less: Cash already paid on account payable balance =$36,900
Balance at the end of march in Accounts payable = $83,900
Therefore, balance left at the end of march is $83900.
Learn more about Account here;
https://brainly.com/question/24159657
#SPJ4
a) use definition 2 to find an expression for the area under the curve y=x^3 from 0 to 1 as a limit.(b) the following formula for the sum of the cubes of the first n integers is proved in Appendix E. useit to evaluate the limit in part (a).1^3 + 2^3 +3^3+.....n^3 = [n(n+1)/2]^2Definition 2: The area A of the region S that lies under the graph of the continuous function f is the limit of the sum of the areas of approximating.
Answers
The area A of the region S that lies under the graph of the continuous function f is \(\frac{1}{4}\).
(a)
\(A =\) \(\int\limits^A_b {f(x)} \, dx\)
= \(\lim_{n \to \infty}\)∑ f(xi) Δ x
a = 0, b = 1 → Δ x = \(\frac{1-0}{n}\) = \(\frac{1}{n}\)
x₀ = 0, x₁ = \(\frac{1}{n}\) , x₂ = \(\frac{2}{n}\), x₃ = \(\frac{3}{n}\), ..., xi = \(\frac{i}{n}\)
f(x) = \(x^{3}\)
f(xi) = \([\frac{i}{n} ]^{3}\) = \(\frac{i^{3} }{n^{3} }\)
Then,
A = \(\lim_{n \to \infty}\) ∑(\(\frac{i^{3} }{n^{3} }\)) * \(\frac{1}{n}\)
(b)
A = \(\lim_{n \to \infty}\) [\(\frac{1}{n}\) * ∑ \(\frac{i^{3} }{n^{3} }\) ]
= \(\lim_{n \to \infty}\) [\(\frac{1}{n}\) * \(\frac{1}{n^{3} }\) ∑ \(i^{3}\)]
= \(\lim_{n \to \infty}\) [\(\frac{1}{n^{4} }\) * [\(\frac{n(n+1)}{2}\)]^2]
= \(\lim_{n \to \infty}\) [\(\frac{1}{n^{4} }\) * \(\frac{n^{2}(n+1)^{2} }{4}\)]
= \(\lim_{n \to \infty}\) \(\frac{(n+1)^{2} }{4n^{2} }\)
= \(\frac{1}{4}\) * \(\lim_{n \to \infty}\) \((\frac{n+1}{n} )^{2}\)
= \(\frac{1}{4}\) * \(1^{2}\)
A = \(\frac{1}{4}\)
Therefore the area A of the region is \(\frac{1}{4}\).
To know more about area here
https://brainly.com/question/14483989
#SPJ4
Select ALL the correct answers.
The base of a pentagon lies on ray AB as shown.
An illustration showing a pentagon lying on ray AB, which when extended forms an exterior angle and is marked as 2x plus 14 degrees. The interior angle next to this exterior angle measures 7x plus 13 degrees.
Determine which statements are true.
(2x + 14)° = 48°
x = 7°
(2x + 14)° + (7x + 13)° = 180°
(7x + 13)° = 132°
(2x + 14)° = 90°
Answers
An illustration showing a pentagon lying on ray AB, which when extended forms an exterior angle and is marked as 2x plus 14 degrees, the correct statements are (2x + 14)° + (7x + 13)° = 180°, (7x + 13)° = 132°, x = 7°.
In the given illustration, we have a pentagon with base AB lying on a line or ray AB. Let's call the first interior angle to the right of the exterior angle marked as 2x + 14 degrees as angle C.
We can see that the sum of the measures of all interior angles of a pentagon is 180 degrees. Hence, the sum of all interior angles of this pentagon is:
C + angle D + angle E + angle F + angle G = (5 - 2) x 180 degrees (since a pentagon has five sides and angles)
(2x + 14)° + (7x + 13)° = 180° (sum of interior angles of a pentagon)
(7x + 13)° = 132° (simplifying the above equation)
x = 7° (solve for x by subtracting 14 from both sides of the first equation)
Therefore, options 2, 3, and 4 are correct.
For more details regarding pentagon, visit:
https://brainly.com/question/17054992
#SPJ1
Market value of bond : $7000
Por volue of bond : $10000
Time to maturity : 8 year Market rate : 15% ( semi annualy )
Q. What is the coupon payment to be every 6 month
Answers
The coupon payment to be paid every 6 months is $375.
The market value of a bond, the par value of a bond, the time to maturity of a bond, and the market rate of interest on a bond are all crucial aspects in determining the coupon payment of a bond.
As a result, to determine the coupon payment, we must first comprehend the terms and then perform calculations.M
The given details are as follows:Market value of bond (MV) = $7000Par value of bond (PV) = $10000Time to maturity (t) = 8 yearsMarket rate of interest (r) = 15% (semi-annually).
To begin, we must determine the amount of interest that will be paid on the bond over the course of a year. Because the market rate is a semi-annual rate, we must first divide it by two, which results in a semi-annual rate of 7.5%.
As a result, the semi-annual interest payment will be calculated using the following formula: Semi-annual interest payment = (Par value of bond × semi-annual interest rate) ÷ 2.
Plugging in the values, we have:Semi-annual interest payment = ($10000 × 7.5%) ÷ 2= ($10000 × 0.075) ÷ 2= $375.
Because interest is paid twice a year (semi-annually), we can see that each interest payment is $375. As a result, the coupon payment every six months would be $375.
Thus, the coupon payment to be paid every 6 months is $375.
To know more about semi-annual interest visit:
brainly.com/question/30573341
#SPJ11
in the diagram below, AB CD and BPT = 118 Calculate the value of x and y.
Answers
The value of x is 36 and the value of y is 108
How to calculate the values of x and y?The diagram that completes the question is added as an attachment
From the figure, we have:
Internal angles within a transversal = 3x and 2x
The sum of these angles is 180 degrees.
So, we have
3x + 2x =180
Evaluate the sum
5x = 180
Divide both sides by 5
x = 36
Also, we have
y = 3x ---- vertical angles
Substitute x = 36 in y = 3x
y = 3 * 36
Evaluate the product
y = 108
Hence, the value of x is 36 and the value of y is 108
Read more about angles at:
https://brainly.com/question/24839702
#SPJ1

A truck that transports refrigerators has a storage compartment 12 feet high by 9 feet wide by 51 feet long. Each refrigerator takes up 54 cubic feet. How many refrigerators can be packed on the truck if there is no wasted space?
Enter a unit that best describes the number.
Answers
Answer:
102
Step-by-step explanation:
12 x 9 x 51 = 5508
5508 / 54 = 102
Hope this helps!
Answer:
102.00
Step-by-step explanation:
12 feet high * 9 feet wide * 51 feet long / 54 = the answer
Shawna bought 2 notebooks that cost $2.19 each. She paid for them with a
$5 bill. Which number sentence can be used to find how much money
Shawna received in change?
A. (2 x 5.00) + 2.19 =
B.
5.00 + (2 x 2.19) =
C.
(2 X 5.00)
2.19
OD 5.00
(2 x 2.19)
