Answers
Answer:
Step-by-step explanation:
Related Questions
Please I really need help!

Answers
Answer: It is D
Step-by-step explanation:

Please help due in 5 minutes !

Answers
Answer:
Step-by-step explanation:pentagon
Hexagon
Heptagon
Octagon
Nonagon
Decagon
I’m sorry if this is wrong
what is what is sixth eighths times five(PLEASE HELP i'M STILL FAILING MATH!!!!!!!!!!!!!!!!!!!!)
Answers
Answer:
\(3\frac{3}{4}\)
Step-by-step explanation:
\(\frac{6}{8} *\frac{5}{1}\)
\(\frac{30}{8}\) multiply across
\(\frac{15}{4}\) simplify and convert into mixed number
\(3\frac{3}{4}\)
Name the property illustrated by if a = -3 and -3 = b, then a = b.
Answers
The Transitive property states that;
if a=b and b=c then a=c.
and c by b.
if a = -3 and -3 = b, then a = b.
So, the property illustrated is similar to the Transitive property
Therefore, the property illustrated is the Transitive property.So, if you replace b with -3 we have;
f
PLS HELP I'LL MARK BRAINLEST

Answers
Answer:
x=60+70=130(exterior angle of a triangle is equal to the sum of two opposite interior angle)
Please answer my question quickly.

Answers
Answer:
b=sqrt7
Step-by-step explanation:
16=9+b^2
to evaluate which of a set of curves fits the data best, we can use: a. APE b. MAPE c. R2 d. NPV
Answers
To evaluate which of a set of curves fits the data best, you can use the option "c. R2", also known as the coefficient of determination.
R2 is a statistical measure that helps determine the proportion of variance in the dependent variable explained by the independent variable(s) in the regression model. It ranges from 0 to 1, with higher values indicating a better fit of the curve to the data.
To evaluate which of a set of curves fits the data best, we can use the R2 (coefficient of determination) metric. R2 is a statistical measure that represents the proportion of the variance in the dependent variable that is explained by the independent variable(s) in a regression model.
A higher R2 value indicates a better fit of the curve to the data. APE (absolute percentage error), MAPE (mean absolute percentage error), and NPV (net present value) are not appropriate metrics for evaluating the fit of a curve to data. APE and MAPE are typically used to measure forecasting accuracy, while NPV is a financial metric used to determine the present value of future cash flows.
Learn more about coefficient of determination
brainly.com/question/28975079
#SPJ11
Help me plsssssssssssssssssssssssssss

Answers
Answer: 120
Step-by-step explanation: divide 24 by 5 to get 4.8 so its 4.8 minutes for one question
25 x 4.8 = 120
Given: ABCD parallelogram BK ⊥ AD , AB = 6, AK = 3 Find: m∠A, m∠B, m∠C, m∠D
Answers
Answer: Angle A = 60°, angle B = 120°, angle C = 60°, angle D = 120°
Step-by-step explanation: Please refer to the attached diagram for further details.
The question has given the parallelogram ABCD as having side AB measuring 6 units, side AK measuring 3 units and line BK has been drawn perpendicular to line AD. This means line AK forms a right angle at the point where it meets line AD. From the information provided and the figure derived from that, we have right angled triangle ABK with the right angle at point K, line AB equals 6 units and line AK equals 3 units.
Using angle A as the reference angle, line AK is the opposite (side facing the reference angle), line AB is the hypotenuse (line facing the right angle) and line AK is the adjacent (side that lies between the right angle and the reference angle).
Hence, using the trigonometric ratios,
Cos A = adjacent/hypotenuse
Cos A = 3/6
Cos A = 0.5
Checking with the calculator, (that is second function of Cos 0.5)
A = 60
The opposite sides of a parallelogram are equal (that is line AD is parallel to line BC) and therefore opposite angles are equal (that is angle A is equal to angle C).
Similarly, angle B is equal to angle D. However, angles in a quadrilateral equals 360 degrees.
Therefore, angles in parallelogram ABCD is derived as;
A + B + C + D = 360
60 + B + 60 + D = 360
120 + B + D = 360
Subtract 120 from both sides of the equation
B + D = 240
Having known that angle B equals angle D, angles B and D is derived as each half of the value 240
Angle B = 240/2
Angle B = 120
and angle D = 120
Therefore, the angles are;
A = 60, B = 120, C = 60, D = 120

1
2
3
X
Numedaya
cling magazine
Number of
megnes sold
a
12
15
21
Tom sold magazines for 4 days last week. The table above gives the total number of magazines Tom had
sold for the week at the end of each of the 4 days. Which of the following best models the relationship
between the total number M of magazines Tom sold and the number x of days selling?
O M(x)=x+4
O M(x)= 1.5x +4
20 M(x)= 4x + 4
> M(x)= 6x+4

Answers
Answer:
C. \( M(x) = 4x + 4 \)
Step-by-step explanation:
Find the rate of change/slope (m) using two pairs (1, 8) and (2, 12):
\( slope (m) = \frac{y_2 - y_1}{x_2 - x_1} = \frac{12 - 8}{2 - 1} = \frac{4}{1} = 4 \)
(Note: M(x) = y)
Find y-intercept (b) by substituting x = 1, M(x) = 8, and m = 4 in M(x) = mx + b.
Thus:
8 = (4)(1) + b
8 = 4 + b
Subtract 4 from each side
8 - 4 = b
4 = b
b = 4
substitute m = 4, and b = 4 in M(x) = mx + b, to get the equation that models the relationship.
The equation would be:
✅ \( M(x) = 4x + 4 \)
how many zeros in a million
Answers
Answer:
There are 6 zeros in one million.
Step-by-step explanation:
1000000 (one million)
6 zeros
-12=24+b how do I solve this

Answers
Answer:
b = -9
Step-by-step explanation:
-12 = 24 + 4b \(\longmapsto\\\) Subtract 24 from both sides
-12 - 24 = 24 + 4b - 24
-36 = 4b \(\longmapsto\\\) Divide all sides by 4
-36 ÷ 4 = 4b ÷ 4
-9 = b
-Chetan K
Answer:
-9 = b
Step-by-step explanation:
-12 = 24 + 4b
-12 - 24 = 4b
\(\frac{-36}{4} = \frac{4b}{4} \\\)
Hope this helps!
Help pls!!!!!!!!!!!!! trigonometry is it cos sin or tan

Answers
Answer:
tan (angle T) = 5/2
angle T = arctan (5/2)
the hexadecimal notation of (1110 1110 1110)2 is
Answers
The hexadecimal notation of (1110 1110 1110)₂ is:
EEE₁₆
1. Break down the binary number into groups of 4 bits:
(1110)₂ (1110)₂ (1110)₂
2. Convert each group into its corresponding hexadecimal value:
- (1110)₂ = 14₁₀ = E₁₆
- (1110)₂ = 14₁₀ = E₁₆
- (1110)₂ = 14₁₀ = E₁₆
3. Combine the hexadecimal values to get the final answer: EEE₁₆
Learn more about hexadecimal values:https://brainly.com/question/13041189
#SPJ11
Can someone help with the third one
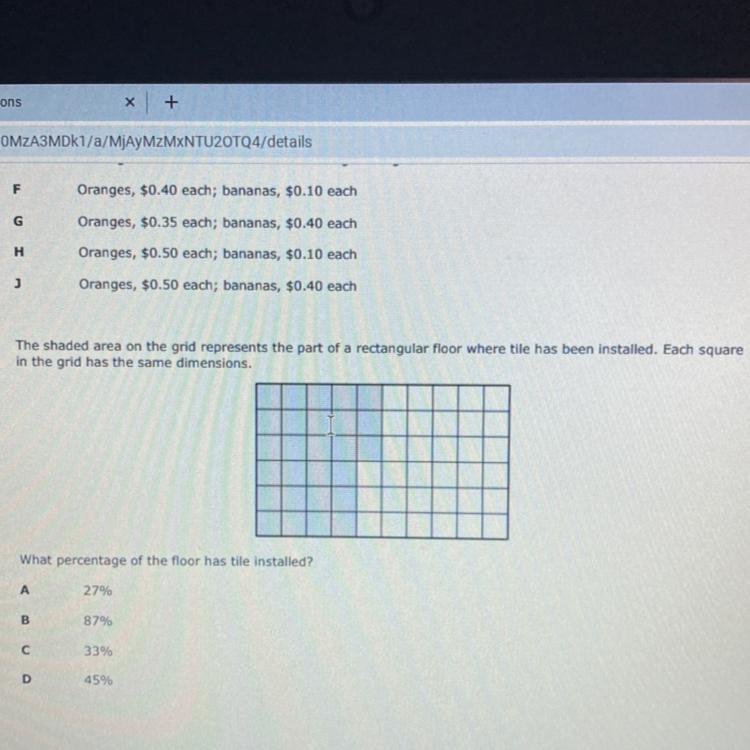
Answers
Answer: 45%
Step-by-step explanation:
27/60 squares are covered
I reduced the fraction to 9/20, multiplied by 5 to make the denominator 100 and the numerator is 45, therefore fraction is 45/100.
Identify the lower class limits, upper class limits, class width, class midpoints, and class boundaries for the given frequency distribution. Also identify the number of individuals included in the summary.
Age (yr) when award was won Frequency
15-24 27
25-34 33
35-44 14
45-54 4
55-64 6
65-74 1
75-84 1
Answers
Lower class limits are 15, 25, 35, 45, 55, 65, 75, Upper class limits are 24, 34, 44, 54, 64, 74, 84, Class width are 10 (all classes have a width of 10), Class midpoints are 19.5, 29.5, 39.5, 49.5, 59.5, 69.5, 79.5, Class boundaries are [15, 25), [25, 35), [35, 44), [45, 54), [55, 64), [65, 74), [75, 84) and Number of individuals included in the summary is 76.
Here are the details for the given frequency distribution:
Lower class limits are the least number among the pair
Here, Lower class limits are 15, 25, 35, 45, 55, 65, 75 respectively.
Upper class limits are the greater number among the pair
Here, upper limit class are 24, 34, 44, 54, 64, 74, 84 respectively.
Class width is the difference between the Lower class limits and Upper class limits which is 10 (all classes have a width of 10).
Class midpoints is the middle point of the lower class limits and Upper class limits which is 19.5, 29.5, 39.5, 49.5, 59.5, 69.5, 79.5 respectively.
Class boundaries are the extreme points of the classes which are [15, 25), [25, 35), [35, 44), [45, 54), [55, 64), [65, 74), [75, 84) respectively.
Number of individuals = 27 + 33 + 14 + 4 + 6 + 1 + 1
= 76
To learn more about Lower class limits here:
https://brainly.com/question/29027902
#SPJ4
An investigator is studying the association between cell phone use and migraine headaches. She recruits 100 cases (migraine patients) and 100 controls (people who don't suffer from migraine), and asks each group how many hours they use their cell phones per day, on average. She obtains the following information:
cases controls
use cellphones
>3hrs/day
60 55
use cellphones
<3hrs/day
40 45
total 100 100
Calculate the observed odds ratio (the observed association between migraine headache and cell phone use).
OR = 0.82
OR = 1.23
OR = 1.11
OR = 3.45
Answers
The observed odds ratio (the observed association between migraine headache and cell phone use) is OR = 1.23.
An investigator is studying the association between cell phone use and migraine headaches.
100 cases (migraine patients) and 100 controls (people who don't suffer from migraine), and asks each group how many hours they use their cell phones per day, on average.
To calculate odd ratio ( exposure is cell phone as to check cell phone use on migraine)
Odds of disease in exposed = 60/55= 1.09
Odd of disease in non exposed = 40/45 = 0.88
Thus the odds ratio will be = 1.09:0.88
=> Odds of disease in exposed / odds of disease in non exposed = 1.09/ 0.88 = 1.23
= OR = 1.23
Hence the answer is the observed odds ratio (the observed association between migraine headache and cell phone use) is OR = 1.23.
To learn more about ratio click here https://brainly.com/question/13513438
#SPJ4
Question 4 (25 pts.) If p is an odd prime, then prove that 1².3²... (p-2)² = (-1) (mod p)
Answers
As we have proved that if p is an odd prime, then the product 1² · 3² · ... · (p-2)² is congruent to -1 modulo p.
To prove the statement, let's consider the product P = 1² · 3² · ... · (p-2)². Our goal is to show that P ≡ -1 (mod p), which means P leaves a remainder of -1 when divided by p.
First, we note that p is an odd prime. This means that p can be expressed as p = 2k + 1, where k is an integer. We can rewrite P using this representation:
P = (1 · 1) · (3 · 3) · ... · ((2k - 1) · (2k - 1)).
Now, let's examine P more closely. We can write each factor in P as:
(2i - 1) · (2k - (2i - 1)).
Expanding this expression, we get:
(2i - 1) · (2k - 2i + 1) = 4ik - 2i + 2ki - k - 2i + 1 = 4ik - 4i + 2ki - k + 1.
We can simplify this further as:
(4ik - 4i + 2ki - k + 1) = (4ik - 4i) + (2ki - k + 1) = 4i(k - 1) + k(2i - 1) + 1.
Now, let's consider the expression (2i - 1) modulo p. Since p = 2k + 1, we can rewrite (2i - 1) as:
(2i - 1) ≡ 2i - 1 (mod p).
Substituting this back into our expression for P, we have:
P ≡ (4i(k - 1) + k(2i - 1) + 1) (mod p).
Now, let's consider the sum (4i(k - 1) + k(2i - 1)) modulo p. We can write this as:
(4i(k - 1) + k(2i - 1)) ≡ 4ik - 4i + 2ki - k ≡ -3i + k(i - 1) (mod p).
Since p = 2k + 1, we have -3i + k(i - 1) ≡ -3i + (p - 1)(i - 1) (mod p).
Expanding (p - 1)(i - 1), we get:
-3i + (p - 1)(i - 1) = -3i + pi - p - i + 1 = -4i - p + pi + 1.
Now, let's consider the expression (-4i - p + pi + 1) modulo p. We can rewrite this as:
(-4i - p + pi + 1) ≡ -4i - p (mod p).
Since -p ≡ 0 (mod p), we have -4i - p ≡ -4i (mod p).
Therefore, we have shown that:
P ≡ -4i (mod p).
Now, let's consider the range of i. We know that i takes on values from 1 to (p - 2)/2, inclusive. Since p is an odd prime, (p - 2)/2 is an integer. Therefore, we can rewrite P as:
P ≡ -4(1 + 2 + 3 + ... + [(p - 2)/2]) (mod p).
The sum 1 + 2 + 3 + ... + n can be expressed as n(n + 1)/2. Substituting this into our expression for P, we get:
P ≡ -2[(p - 2)/2] [(p - 2)/2 + 1] (mod p).
Simplifying further, we have:
P ≡ -[(p - 2)/2] [(p - 2)/2 + 1] (mod p).
Since p is an odd prime, we can rewrite p - 2 as 2k - 1. Substituting this into our expression, we get:
P ≡ -[k] [k + 1] (mod p).
Now, let's expand the product [k] [k + 1]:
[k] [k + 1] = k² + k.
Substituting this back into our expression for P, we have:
P ≡ -(k² + k) (mod p).
Now, recall that p = 2k + 1. Substituting this into our expression, we get:
P ≡ -(k² + k) ≡ -(k² + k + 1) + 1 ≡ -(k² + 2k + 1) + 1 ≡ -[(k + 1)²] + 1 (mod p).
Since p = 2k + 1, we have (k + 1)² ≡ -1 (mod p). Substituting this back into our expression, we finally have:
P ≡ -[(k + 1)²] + 1 ≡ -1 + 1 ≡ 0 ≡ -1 (mod p).
To know more about prime here
https://brainly.com/question/30646191
#SPJ4
FIND THE VALUE OF X (problem in picture, geometry)

Answers
Answer:
x = 12
Step-by-step explanation:
The sum of the 3 angles in a triangle = 180°
Sum the 3 angles and equate to 180
8x - 1 + 3x + 4 + 3x + 9 = 180 , that is
14x + 12 = 180 ( subtract 12 from both sides )
14x = 168 ( divide both sides by 14 )
x = 12
Which face of the rectangular prism has the same shape and dimensions as the cross section shown in the figure? Select all that apply.

Answers
2 Answers:
C) left faceF) right face====================================
Explanation:
The left and right walls are mirror copies of one another, and they are also copies of the cross section as well. Think of a subdivision to divide one room into two smaller ones. That middle wall is the same as the left and right walls of the original larger room. Effectively, those two smaller rooms are blocks of their own we can pull apart or cut.

4 solve the following simultaneous equations using elimination method:
(iii) 2x - y = 2, 5x + y = -9
Answers
Step-by-step explanation:
As instructed
Use Elimination Method....
2x - y = 2
2x - 2 = y
y = 2x - 2 ----------- equation 1
5x + y = -9
Substitute for y
5x + 2x - 2 = -9
7x = -9 + 2
7x = -7
x = -7/7
x = -1
Substitute for x in equation 1
y = 2x - 2
y = 2(-1) - 2
y = -2 - 2
y = -4
Answer:
(- 1, - 4 )
Step-by-step explanation:
Given the 2 equations
2x - y = 2 → (1)
5x + y = - 9 → (2)
Adding the 2 equations term by term will eliminate the y- term, that is
7x + 0 = - 7
7x = - 7 ( divide both sides by 7 )
x = - 1
Substitute x = - 1 into either of the 2 equations and solve for y
Substituting into (2)
5(- 1) + y = - 9
- 5 + y = - 9 ( add 5 to both sides )
y = - 4
solution is (- 1, - 4 )
graph the curve with parametric equations x = sin(t), y = 3 sin(2t), z = sin(3t).
Find the total length of this curve correct to four decimal places.
Answers
The curve with parametric equations x = sin(t), y = 3sin(2t), z = sin(3t) can be graphed in three-dimensional space. To find the total length of this curve, we need to calculate the arc length along the curve.
To find the arc length of a curve defined by parametric equations, we use the formula:
L = ∫ sqrt((dx/dt)^2 + (dy/dt)^2 + (dz/dt)^2) dt
In this case, we need to find the derivatives dx/dt, dy/dt, and dz/dt, and then substitute them into the formula.
Taking the derivatives:
dx/dt = cos(t)
dy/dt = 6cos(2t)
dz/dt = 3cos(3t)
Substituting the derivatives into the formula:
L = ∫ sqrt((cos(t))^2 + (6cos(2t))^2 + (3cos(3t))^2) dt
To calculate the total length of the curve, we integrate the above expression with respect to t over the appropriate interval.
After performing the integration, the resulting value will give us the total length of the curve. Rounding this value to four decimal places will provide the final answer.
Learn more about integrate here:
https://brainly.com/question/30217024
#SPJ11
A typical person begins to lose consciousness if subjected to accelerations greater than about 5 g(49.0 m/s^2) for more than a few seconds. Suppose a 3.00×10^4−kg manned spaceship's engine has an exhaust speed of 2.50×10^3 m/s. What maximum burn rate ∣ΔM/Δt∣ could the engine reach before the ship's acceleration exceeded 5 g and its human occupants began to lose consciousness?
Answers
The maximum burn rate ∣ΔM/Δt∣ that the engine could reach before the ship's acceleration exceeded 5 g and its human occupants began to lose consciousness is approximately 51.0 kg/s.
Acceleration is directly proportional to the force acting on an object. In simple terms, if the force on an object is greater, then it will undergo more acceleration. However, there are limitations to the acceleration that can be tolerated by the human body. At about 5 g (49.0 m/s2) for more than a few seconds, an average person starts to lose consciousness. Let's use this information to answer the given question.
Let the maximum burn rate |ΔM/Δt| that the engine could reach before the ship's acceleration exceeded 5 g be x.
Let the mass of the spaceship be m and the exhaust speed of the engine be v.
Using the formula for the thrust of a rocket,
T = (mv)e
After substituting the given values into the formula for thrust, we get:
T = (3.00 × 104)(2.50 × 103) = 7.50 × 107 N
Therefore, the acceleration produced by the engine, a is given by the formula below:
F = ma
Therefore,
a = F/m= 7.50 × 107/3.00 × 104= 2.50 × 103 m/s²
The maximum burn rate that the engine could reach before the ship's acceleration exceeded 5 g is equal to the acceleration that would be produced by a maximum burn rate. Therefore,
x = a/5g= 2.50 × 103/(5 × 9.8)≈ 51.0 kg/s
Therefore, the maximum burn rate ∣ΔM/Δt∣ that the engine could reach before the ship's acceleration exceeded 5 g and its human occupants began to lose consciousness is approximately 51.0 kg/s.
Learn more about maximum burn rate
https://brainly.com/question/29328145
#SPJ11
What are Absolute Values
Answers
Absolute values are non-negative value of a number. it can denote the distance of a number from zero
Write an expression that tells you how fast height is changing, with respect to time, after a seconds have passed.
Answers
find the volume of a cylinder with a diameter of 22 yd and a height of 7 yd

Answers
V=π(d
2)2h=π·(20.12
2)2·6.4≈2034.42618m
Put the following equation of a line into slope-intercept form. 12x-4y=12 Must be FULLY SIMPLIFIED.
Answers
The slope intercept form has the next form
\(y=mx+b\)We have
\(12x-4y=12\)we need to isolate the y
\(-4y=-12x+12\)\(y=\frac{-12}{-4}x+\frac{12}{4}\)\(y=3x-3\)ANSWER
y=3x-3
What is three and seventeen-thousandths written in standard form?
Answers
Answer:
Step-by-step explanation:
That would be 3.017: three and seventeen thousandths
If angle 3 = 81, what is angle 4?

Answers
Answer:
99 degrees
Step-by-step explanation:
Angle 3 and 4 added together is 180 degrees since it is a straight line.
if you know angle 3 is 81 degrees, then angle 4=180-81=99
Answer:
99 is the measure of angle 4
Step-by-step explanation:
Two parralel lines cut by a transversal.
This is all you gotta remember
Alternate interior angles (4 and 6, 3 and 5) are congruent (equal)
Altenrate exterior angles (1 and 7, 2 and 8) are congruent (equal)
Corresponding angles (2 and 6, 3 and 7, 1 and 5, 4 and 8) are congruent (equal)
Same side interior angles (3 and 6, 4 and 5) are supplementary (equal to 180 if added up)
Same side exterior angles, (2 and 7, 1 and 8) are supplementary (Equal to 180 if added up)
Same line, opposite transversal (4 and 3, 5 and 6, 8 and 7, 1 and 2) are also supplementary.
Answer the photo below thanks

Answers
Step-by-step explanation:
3 of the 4 options aren't prisms
A is a cuboid
B is a cube
C is a prism
D is a pyramid
Answer:
The answer is D.
I hope this helps.
Have nice day/night!!!!(wherever you are)
