Answers
Answer:
90
Step-by-step explanation:
PVQ = 60 an RVS = 30, 60 + 30 = 90
Related Questions
the periodic transfer of a portion of the cost of an intangible asset to expense is referred to as
Answers
The periodic transfer of a portion of the cost of an intangible asset to expense is known as amortization. This is the process of spreading the cost of an intangible asset over its useful life, similar to how depreciation is used for tangible assets like buildings and equipment.
Intangible assets, such as patents, copyrights, and trademarks, do not have a physical existence but still have value to the company. Amortization recognizes the decline in value of these assets over time and helps to accurately reflect their impact on the company's financial statements.
The amount of amortization each period is calculated by dividing the cost of the asset by its estimated useful life. It is important for companies to track and properly account for their intangible assets, including amortization, as it can have a significant impact on their financial statements and overall financial health.
To know more about amortization refer here
https://brainly.com/question/29643279#
#SPJ11
once the component fails, it is immediately replaced byanother one of the same type. if we let denote the life-time of the th component to be put in use, then represents the time of the th failure. the long-term rate at which failures occur, call it , is defined by
Answers
The long term rate is defined by r = 3/2.
Probability deals with the likelihood of an event or phenomena occurring and is quantified as a number between 0 and 1 inclusive, where 0 indicates an impossible chance of occurrence and 1 denotes the certain outcome of an event. Joint probability refers to a statistical measure that determines the probability of two events occurring together and at the same point in time. Joint probability is the probability of event Y occurring at the same time that event X occurs. Hence, joint probability is a measure of two events happening at the same time and can only be applied to situations where more than one observation can occur at the same time.
A random variable with probability density function is f(x) = 2x, 0 <x<1.
Let Xi denote the life-time of the ith component , then Sn = ∑Xi represents the time of the nth failure. The long-term rate failures occur, is defined by
\(r = \lim_{n \to \infty} \frac{n}{S_n}\)
Let Xi denote the ith component and understand that X1, X2,.., is a sequence of independent and similarly distributed random variables, with finite mean.
\(Mean = E[Xi] = \int\limits^0_1 {xf(x)} \, dx = \int\limits^0_1 {2x^{2} } \, dx = \frac{2}{3}\)
So,
\(r = \lim_{n \to \infty} \frac{n}{S_n} = \frac{1}{Mean} = \frac{3}{2}\)
Thus, the long term rate is defined by r = 3/2.
To learn more about probability, visit brainly.com/question/30034780
#SPJ4
The long term rate is defined by r = 3/2.
Probability deals with the likelihood of an event or phenomena occurring and is quantified as a number between 0 and 1 inclusive, where 0 indicates an impossible chance of occurrence and 1 denotes the certain outcome of an event. Joint probability refers to a statistical measure that determines the probability of two events occurring together and at the same point in time. Joint probability is the probability of event Y occurring at the same time that event X occurs. Hence, joint probability is a measure of two events happening at the same time and can only be applied to situations where more than one observation can occur at the same time.
A random variable with probability density function is f(x) = 2x, 0 <x<1.
Let Xi denote the life-time of the ith component , then Sn = ∑Xi represents the time of the nth failure. The long-term rate failures occur, is defined by
\(r = \lim_{n \to \infty} \frac{n}{S_n}\)
Let Xi denote the ith component and understand that X1, X2,.., is a sequence of independent and similarly distributed random variables, with finite mean.
\(Mean = E[X_i] = \int\limits^0_1 {x} f(x) \, dx =\int\limits^0_1 {2x^2} \, dx =\frac{2}{3}\)
So,
\(r = \lim_{n \to \infty} \frac{a_n }{S_n} = \frac{1}{mean} = \frac{3}{2}\)
To learn more about probability
brainly.com/question/30034780
#SPJ4
I I need help on number 25 please

Answers
Answer:
22
Step-by-step explanation:
First write an expression to represent the situation.
$1,300,000 ≤ $475,000 + $37,500a
This expression works because the least amount of money that can make to remain profitable is 1,300,000. They already have 475,000 of that and every a (number of ads sold) is $37,500
Using this equation, solve for a.
1300000 ≤ 475000 + 37500a
First, subtract 475000 from both sides.
825000 ≤ 37500a
Then divide both sides of the equation by 37500 to isolate a.
22 ≤ a
22 is less than or equal to a. So they must sell at least 22 ads to remain profitable.
Calculate the perimeter and area of the shaded region in the drawing of two circles at right. Round to the nearest tenth. Show all work. 10 5cm 21 cm
Answers
The perimeter of the shaded region is approximately 85.67 cm The area of the shaded region is approximately 91.84 cm² (rounded to the nearest tenth).
To calculate the perimeter and area of the shaded region, we first need to find the radius of each circle.
The larger circle has a diameter of 21 cm, which means its radius is 10.5 cm (half of the diameter). The smaller circle has a diameter of 10 cm, so its radius is 5 cm.
To find the perimeter of the shaded region, we need to add the circumference of both circles and subtract the overlap (the length of the shared segment). The circumference of the larger circle is 2π(10.5) ≈ 65.97 cm, and the circumference of the smaller circle is 2π(5) ≈ 31.42 cm.
To find the length of the shared segment, we can use the Pythagorean theorem. The distance between the centers of the circles is 15 cm (the sum of the radii), so we can form a right triangle with legs of 10.5 cm and 5 cm. Using the Pythagorean theorem, we get:
c² = a² + b²
c² = 10.5² + 5²
c² ≈ 137.25
c ≈ 11.72
So the length of the shared segment is approximately 11.72 cm.
Therefore, the perimeter of the shaded region is approximately 65.97 + 31.42 - 11.72 = 85.67 cm (rounded to the nearest tenth).
To find the area of the shaded region, we need to subtract the area of the smaller circle from the area of the larger circle, and then subtract the area of the overlap (the area of the shared segment).
The area of the larger circle is π(10.5)² ≈ 346.36 cm², and the area of the smaller circle is π(5)² ≈ 78.54 cm².
To find the area of the shared segment, we can use the formula for the area of a sector of a circle:
A = (θ/360)πr²
where θ is the central angle of the sector. In this case, the sector has a central angle of 2cos⁻¹(5/10.5) ≈ 105.2°, so:
A = (105.2/360)π(10.5)²
A ≈ 91.84 cm²
Know more about perimeter here:
https://brainly.com/question/6465134
#SPJ11
SOMONE PLEASEE HELPPP MEEEEEEEE!!!

Answers
Answer:
? = 36 degrees
Step-by-step explanation:
To find this measure, we use the appropriate trigonometric ratio
from the question, the angle faces the length 26 which represents the opposite
the length 44 faces the angle 90, which is the hypotenuse
The trigonometric ratio that connects both is the sine
The sine of an angle is the ratio of the opposite to the hypotenuse
Thus;
sine ? = 26/44
? = arc sine (26/44)
? = 36
Part B Using squares 1, 2, and 3, and eight copies of the original triangle, you can create squares 4 and 5. Keep the square 4 and square 5 window open. You will need them to complete the rest of the tasks in this section. What are the side lengths of square 4 and square 5 in terms of a and b? Do the two squares have the same area?
Answers
The 4 sides of a square are usually the same and the side length of squares 4 and 5 is a+b.
How to explain the square?From the diagram, each side is called the side length. Therefore,
Side length of square 4 = a + bSide length of square 5 = a + bIf the side lengths are equal that is (a + b), then the area which is the square of the side length will also be the same.
Learn more about square on:
https://brainly.com/question/25092270
ellen makes cookies and sells them at the local farmers' market. today, she is going to make batches of her famous cardamom cookies. she has a jar with 2 fluid ounces of cardamom, and her recipe calls for 1 4/5 tablespoons, or 3/10 of a fluid ounce, of cardamom in each batch. how many batches can ellen make with all of her cardamom?
Answers
Ellen can make a maximum of 6 batches of Cardamom cookies with her 2 fluid ounces of cardamom.
Ellen has 2 fluid ounces of cardamom in a jar. Her recipe requires 3/10 of a fluid ounce of cardamom for each batch of cardamom cookies.
We can use division to find the number of batches of cardamom cookies that Ellen can make with all of her cardamom:
2 fluid ounces ÷ (3/10 fluid ounce per batch) = (2/1) ÷ (3/10)
= (2/1) x (10/3)
= 20/3
= 6 2/3
Therefore, Ellen can make 6 batches of cardamom cookies with her 2 fluid ounces of cardamom, with 2/3 of a batch remaining.
Since she cannot make a fraction of a batch, Ellen can make a maximum of 6 batches of cardamom cookies with her 2 fluid ounces of cardamom.
To know more about Cardamom cookies .
https://brainly.com/question/31945877
#SPJ11
determine the graph of the polar equation 9/1-3sin theta
Answers
Answer: can you show us the graph?
Step-by-step explanation:
True or false ? Is f(x) a function

Answers
Answer:
true
Step-by-step explanation:
9. sonja is cutting wire to construct a mobile. she cuts 100 inches for the first piece, 80 inches for the second piece. and 64 inches for the third piece. assuming the pattern continues, write an explicit formula for the nth piece. sonja only has 40 feet of wire to use for the project and wants to cut 20 pieces total for the mobile using her pattern. will she have enough wire? justify your answer.
Answers
Total length of wire = 8.33 + 6.67 + 5.33 + ...20 terms= 100[2 - 0.8^20] / [1.2]≈ 80.99 feet Since the total length of wire required is less than the available wire, Sonja will have enough wire.
Given, Sonja cuts 100 inches for the first piece, 80 inches for the second piece, and 64 inches for the third piece. We need to find the explicit formula for the nth piece.We can see that Sonja is cutting wire in decreasing order of 20%.So, the explicit formula for the nth piece can be given by an = a1 * r^(n-1)where a1 = 100 and r = 0.8 Thus, the explicit formula for the nth piece can be given byan = 100 * (0.8)^(n-1)Now, we need to find if Sonja has enough wire for the mobile as she only has 40 feet of wire to use for the project and wants to cut 20 pieces total for the mobile using her pattern.We know that 1 inch = 0.0833 feet 100 inches = 100 * 0.0833 feet = 8.33 feet80 inches = 80 * 0.0833 feet = 6.67 feet64 inches = 64 * 0.0833 feet = 5.33 feet Now, we can find the total length of wire Sonja needs to cut 20 pieces. Therefore, she can complete the mobile using the given pattern.
for more search question length
https://brainly.com/question/28108430
#SPJ8
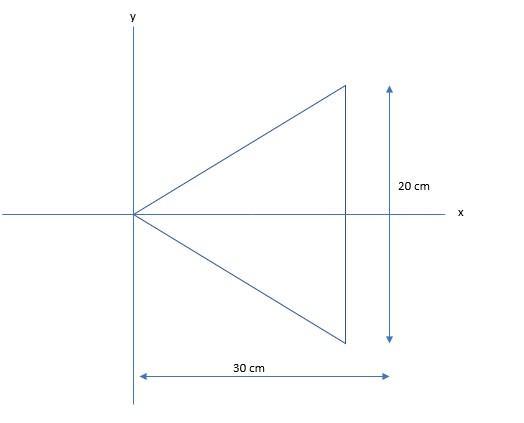
an 800 g steel plate has the shape of the isosceles triangle shown in the figure(figure 1).
Answers
The x- and y-coordinates of the center of mass are; (20, 0)
What is the center of mass of an object?The center of mass is the location where the sum of the relative position of the masses in a mass distribution is zero. It is the point where force can be applied on the distributed mass without causing a rotation of the system.
The mas of the steel plate = 800 g = 0.8 kg
The base length of the isosceles triangular plate = 20 cm = 0.2 m
The height of the isosceles triangular plate = 30 cm = 0.3 m
Considering a small strip of height, dx and width, I, we get
Area of small strip, dA = I·dx
Density of the plate for a unit thickness, ρ = M/A
Density of the small strip of mass dm = dm/dA
Considering the density of the plate as uniform, we get;
\(\displaystyle {\frac{dm}{dA} =\frac{M}{A}\)
Therefore;
\(\displaystyle {dm=\frac{M}{A}\times dA}\)
The area of the triangular plate, A = (1/2) × 0.2 m × 0.3 m = 0.03 m²
Mass of the plate, M = 0.8 kg
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx}\)
The width of the small strip, I, located at a distance x from the vertex of the triangular plate, using similar triangles, indicates;
\(\dfrac{I}{20} = \dfrac{x}{30}\)
\(I=20\times \dfrac{x}{30} = \dfrac{2}{3} \cdot x\)
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx} = \frac{0.8}{0.03}\times \dfrac{2}{3} \cdot x\cdot dx}\)
The center of mass, \(x_{cm}\), can be obtained with the formula; \(\displaystyle {x_{cm} = \dfrac{1}{M} \cdot \int\limits {x} \, dm }\)
Therefore; \(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx }\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx } = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0\)
\(\displaystyle {x_{cm} = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0=\frac{200}{9} \times \frac{0.027}{3} =0.2\)
The location of the x-coordinate center of mass, \(x_{cm}\) = 0.2 m = 20 cm from the vertex, which is the same location as the x-coordinate of the centroid of the plate of uniform density.
The plate is symmetrical about the x-axis, therefore, the y-coordinate of the center of mass is along the x-axis, which is \(y_{cm}\) = 0
The coordinate of the center of mass = (0.2, 0)
Part of the question requires the location of the coordinate of the center of mass of the triangular plate
Learn more about the center of mass of regular shapes here:
https://brainly.com/question/28021242
#SPJ1

determine whether the planes are parallel, perpendicular, or neither. 15x − 3y 12z = 2, 2y = 10x 8z
Answers
The given equations of planes are: 15x - 3y + 12z = 2 & 2y = 10x - 8z
To determine whether these planes are parallel, perpendicular or neither, we need to compare the normal vectors of the planes. The normal vector of a plane is given by the coefficients of x, y and z in the equation of the plane.
The normal vector of the first plane (1) is [15, -3, 12] and the normal vector of the second plane (2) is [10, 2, -8/2] = [10, 2, -4].
Now, to check if the planes are parallel or perpendicular, we can take the dot product of the normal vectors. If the dot product is 0, then the planes are perpendicular, and if it is non-zero, then the planes are parallel.
The dot product of the normal vectors of the given planes is:
[15, -3, 12] · [10, 2, -4] = (15)(10) + (-3)(2) + (12)(-4) = 0
Since the dot product is zero, the planes are perpendicular to each other.
To learn more about planes click here :
brainly.com/question/13792781
#SPJ11
In 1991 there was 1 website. In 1992 there were 10 websites. Work out the percentage change in the number of websites from 1991 to 1992.
Answers
The percentage change in the number of websites from 1991 to 1992 is 900%.
Given that,
In 1991 there was 1 website.
In 1992 there were 10 websites.
The formula to find the percentage change is,
Percent change = (New value - old value) / old value
Here,
New number of websites = 10
Old number of websites = 1
Percentage change = (10 - 1) / 1 = 9 = 900%
Hence the percentage change in the number of websites is 900%.
Learn more about Percentage change here :
https://brainly.com/question/31060287
#SPJ1
4. When you convert from feet to inches, you are doing which of the following?
changing the measurement unit
Determining mass
Determining capacity
Determining volume
Answers
Answer:
A) Changing the measurement unit.
Step-by-step explanation:
"Changing the measurement unit" is the correct answer because when you convert from feet to inches, you are essentially changing the unit of measurement from a larger unit (feet) to a smaller unit (inches) within the same system of measurement (length or distance). It involves multiplying the value in feet by a conversion factor to obtain the equivalent value in inches. This process is commonly used in math, science, and everyday life when dealing with different units of measurement.
Calculate the 95onfidence interval for the true population mean based on a sample with x¯=225, s=8.5, and n=45.
Answers
The 95% confidence interval for the true population mean based on a sample is (222.52, 227.48)
We know that, the confidence interval is:
\(\bar{x}\pm z\frac{\sigma}{\sqrt{n} }\)
where,
\(\bar{x}\) is the sample mean.
z is the critical value.
n is the sample size.
σ (OR s) is the standard deviation for the population.
In this question, we need to calculate the 95% confidence interval for the true population mean based on a sample.
So, \(\alpha=0.95\)
z is the value of Z that has a p-value of \(\frac{1+0.95}{2} =0.975\) , so the critical value is z = 1.96
We have been given x¯=225, s = 8.5, and n = 45.
\(\Rightarrow \bar{x}+ z\frac{s}{\sqrt{n} }\\\\ = 225+1.96\frac{8.5}{\sqrt{45} }\\\\=227.48\)
And,
\(\Rightarrow \bar{x}- z\frac{s}{\sqrt{n} }\\\\ = 225-1.96\frac{8.5}{\sqrt{45} }\\\\=222.52\)
Therefore, the 95% confidence interval for the true population mean based on a sample is (222.52, 227.48)
Learn more about the confidence interval here:
https://brainly.com/question/28064687
#SPJ4
Find an equation of a square root curve of the form
= √ + that approximately contains the points
(3,7) and (6, 8)
Answers
Answer:
y = √(5x+34)
Step-by-step explanation:
The regression formula that matches a square root function to these points can be worked out by a suitable calculator. The attachments shows the points are matched exactly by the function ...
y = √(5x+34)
__
If you would like to work this by hand, you can put the (x, y) point values into the proposed equation and see what the coefficients need to be:
y = √(ax +b)
7 = √(3a +b) ⇒ 49 = 3a +b
8 = √(6a +b) ⇒ 64 = 6a +b
Subtracting the first equation from the second, gives ...
(64) -(49) = (6a +b) -(3a +b)
15 = 3a ⇒ a = 5
49 = 3(5) +b ⇒ b = 34

What is meant by associative property, commutative property and distributive property?
Answers
The commutative, associative, and distributive properties are the properties of addition and multiplication.
The associative and commutative characteristics in mathematics are constant rules that apply to addition and multiplication.
The commutative property states that moving numbers about will still result in the same answer, while the associative property states that rearranging the numbers will provide the same result.
The distributive property states that multiplying the sum of two or more addends by a number yields the same outcome as multiplying each addend separately by the number and combining the resulting products.
To know more about commutative, associative, and distributive property here:
brainly.com/question/12192455#
#SPJ4
Answer:
The distributive property tells us how to solve equations in the form of a(b + c). The distributive property is sometimes called the distributive law of multiplication and division. Normally when we see an equation like this … 4(8+3) distributive property format 4(8+3) -> 4(11) -> 44 we just evaluate what’s in the parentheses first, then solve it: 4(8+3)=4x8 + 4x3=44 These are the 2 methods
Step-by-step explanation:
Find m∠R. please hurry for 50 points!!!

Answers
Answer:
124
Step-by-step explanation:
The sum of interior angles in a triangle is equal to 180:
m<R + m<S + m<T = 180
11x + 3 + x + 15 + 2x + 8 = 180 add like terms
14x + 26 = 180 subtract 26 from both sides
14x = 154 divide both sides by 14
x = 11 to find m<R replace x with 11
11*11 + 3 = 124
Apply angle sum property
\(\\ \rm\rightarrowtail 11x+3+x+15+2x+8=180\)
\(\\ \rm\rightarrowtail 14x+26=180\)
\(\\ \rm\rightarrowtail 14x=154\)
\(\\ \rm\rightarrowtail x=11\)
m<R=11(11)+3=124How do you solve inequality questions?
Answers
An inequality like the statement, x + 3 > 5, can be solved by finding the value of the variable, "x", which is x > 2.
How to Solve an Inequality Question?Inequalities are used to express relationships between quantities or values that are not equal. They can be used to describe constraints or limitations on a solution to a problem, or to represent a range of possible values.
Inequality can also be used to describe relationships between variables in algebraic expressions or equations.
To solve an inequality, we need to isolate the variable in the given statement to determine the value of the variable.
For example, given the inequality, x + 3 > 5, in order to solve this inequality, we need to find the value of x by subtracting 3 from both sides:
x + 3 - 3 > 5 - 3
x > 2.
Learn more about solving inequality on:
https://brainly.com/question/24372553
#SPJ1
HELP!!!! I NEED THIS ASAP PLEASE!!!
Which ordered pair is a solution to the system of equations?

Answers
\(\left \{ {{y=5x} \atop {y=4x+1}} \right.\)
answer is option 2 : (1, 5) because:
when x = 1 , y should = 5:
\(\left \{ {{y=5x} \atop {y=4x+1}} \right.\\\\\left \{ {{y=5(1)} \atop {y=4(1)+1}} \right.\\\\\left \{ {{y=5} \atop {y=5}} \right.\)
13) This is a number wall. To find the number in each block you add the numbers in two blocks below. Find the value of y in this wall. 2 25 y 9 4/8 ●●●
Answers
The value of y is 7.
We have the structure
25
a b
2 y 9
So, (2+y) = a
and, y +9 = b
Then, a+ b= 25
2 +y + y + 9= 25
2y + 11 = 25
2y = 14
y= 7
Thus, the value of y is 7.
Learn more about Algebra here:
https://brainly.com/question/24875240
#SPJ1
use the difference of two squares theorem to find the solution to each equation

Answers
We will investigate how to use the difference of two squares theorem to determine a solution to the equation.
The equation at hand is as follows:
\((\text{ x + }\frac{1}{7})^2\text{ = 8}\)We will move all the terms on the left hand side of the " = " sign as follows:
\((\text{ x + }\frac{1}{7})^2\text{ - 8 = 0}\)The difference of two squares theorem states that:
\(a^2-b^2\text{ = ( a + b ) }\cdot\text{ ( a - b )}\)We see from the above form that we have the following:
\(\begin{gathered} a\text{ = x + }\frac{1}{7} \\ \\ b\text{ = }\sqrt[]{8} \end{gathered}\)Using the difference of two squares formulation we can re-write as a multiple of two factors:
\((\text{ x + }\frac{1}{7})^2\text{ - 8 }\equiv\text{ ( x + }\frac{1}{7}\text{ + }\sqrt[]{8}\text{ ) }\cdot\text{ ( x + }\frac{1}{7}\text{ -}\sqrt[]{8}\text{ )}\)Then the factorized equation becomes:
\(\text{ ( x + }\frac{1}{7}\text{ + }\sqrt[]{8}\text{ ) }\cdot\text{ ( x + }\frac{1}{7}\text{ -}\sqrt[]{8}\text{ ) = 0}\)The solution of the equation becomes:
\(\begin{gathered} x\text{ = - }\frac{1}{7}\text{ - }\sqrt[]{8} \\ \\ x\text{ = }\sqrt[]{8}-\frac{1}{7} \end{gathered}\)We can condense our solution in the form:
\(x\text{ = - }\frac{1}{7}\pm2\sqrt[]{2}\)Which graph corresponds to the table below?



Answers
Answer:
Graph Y
Step-by-step explanation:
This is since the points on the table match up with the line on the Y graph.
which expression fails to compute the area of a triangle having base b and height h (area is one-half base time height)?a.(1.0 / 2.0 ) * b * hb.(1 / 2) * b * hc.(b * h) / 2.0d.0.5 * b * h
Answers
The expression that fails to compute the area of a triangle correctly is option b: (1 / 2) * b * h.
The correct formula to compute the area of a triangle is one-half times the base multiplied by the height, which can be written as (1/2) * b * h. Option a, c, and d correctly represent this formula. However, option b is incorrect because it uses integer division instead of decimal division.
In option b, (1 / 2) is computed using integer division, which results in truncating the decimal part. Therefore, (1 / 2) evaluates to 0 instead of 0.5. As a result, the expression (1 / 2) * b * h would yield incorrect and significantly smaller results than the actual area of the triangle.
To accurately calculate the area of a triangle using this formula, it is essential to use decimal division or explicitly represent the fraction as a decimal. Options a, c, and d correctly account for this by using either 1.0/2.0 or 0.5, ensuring the proper calculation of the area.
Learn more about area of a triangle here:
https://brainly.com/question/27683633
#SPJ11
Jamal is building a bed for his dog the dimensions of the bed or 27 in by 36 in what is the area of the bottom of the bed
Answers
The bottom of the bed has an area of 972 square inches, which is calculated by multiplying 27 inches by 36 inches.
To calculate the area of the bottom of the bed, you must first measure the length and width of the bed. In this case, the length is 27 inches and the width is 36 inches. To calculate the area, you must multiply these two dimensions together. To do this, multiply 27 inches by 36 inches. This will give you the answer of 972 square inches, which is the area of the bottom of the bed. This answer is the total square inches of the bottom surface of the bed. To verify the answer, you can calculate the area of each side individually, and then add them together to get the total area. For example, 27 inches multiplied by 36 inches will give you 972 square inches. If you add the area of the other two sides, you will get the same answer. This shows that the area of the bottom of the bed is 972 square inches.27 inches x 36 inches = 972 square inches
Learn more about area here
https://brainly.com/question/13194650
#SPJ4
4. A pizza shop has 12" pizzas with 6 slices and 16" pizzas with slices. Which pizza has bigger slices?
Answers
Rectangle ABCD and DEFG are congruent
AB=7cm
AD=17cm
Work out the length of CE
Answers
We have the length of CE as 18.4 cm.
Since the rectangles ABCD and DEFG are congruent, all sides of rectangle ABCD will be equal to the corresponding sides of rectangle DEFG. Since AB = 7 cm and AD = 17 cm in rectangle ABCD, we can conclude that DE = 7 cm and DF = 17 cm in rectangle DEFG.
Since CE is a diagonal of rectangle DEFG, it can be found using the Pythagorean theorem. In a rectangle, the diagonal is the hypotenuse of a right triangle formed by one side and one side's corresponding side.
Therefore, CE = √(DE² + DF²) = √(7² + 17²) = √(49 + 289) = √(338) = 18.4 cm
Therefore, the length of CE is 18.4 cm.
To learn more about the Pythagorean theorem,
Visit; brainly.com/question/14930619
#SPJ4
2. Find the measure of x, y, and zº:
35%
X/Yº
700
29

Answers
Answer:
Z=44° X=114° Y=66°
Step-by-step explanation:
Angles in a triangle add up to 180
31°+35°+x°=180°
66°+x°=180°
x°=180°-66°
x°=114°
Angles on a line add up to 180°
x°+y°= 180°
where x°=114°
114°+y° =180°
y°=180°-114°
y°=66°
Angles in a triangle add up to 180
z°+y°+70°=180°
where y=66°
z°+66°+70°=180°
z°+136°=180°
z°=180°-136°
z°=44°
a suburban hotel derives its revenue from its hotel and restaurant operations. the owners are interested in the relationship between the number of rooms occupied on a nightly basis and the revenue per day in the restaurant. following is a sample of 25 days (monday through thursday) from last year showing the restaurant income and number of rooms occupied. day revenue occupied day revenue occupied 1 $ 1,452 30 14 $ 1,425 31 2 1,361 29 15 1,445 34 3 1,426 31 16 1,439 34 4 1,470 32 17 1,348 31 5 1,456 32 18 1,450 30 6 1,430 32 19 1,431 30 7 1,354 29 20 1,446 31 8 1,442 30 21 1,485 34 9 1,394 32 22 1,405 30 10 1,459 32 23 1,461 32 11 1,399 31 24 1,490 30 12 1,458 31 25 1,426 30 13 1,537 34 click here for the excel data file a. choose the scatter diagram that best fits the data. scatter diagram 1 scatter diagram 2 scatter diagram 3 multiple choice scatter diagram 1 scatter diagram 2 scatter diagram 3 b. determine the coefficient of correlation between the two variables. (round your answer to 3 decimal places.) c-1. state the decision rule for 0.01 significance level: h0: rho ≤ 0; h1: rho > 0. (round your answer to 3 decimal places.) c-2. compute the value of the test statistic. (round your answer to 2 decimal places.) c-3. is it reasonable to conclude that there is a positive relationship between revenue and occupied rooms? use the 0.01 significance level. d. what percent of the variation in revenue in the restaurant is accounted for by the number of rooms occupied? (round your answer to 1 decimal place.)
Answers
Attached is a plot that compares the two variables, income and revenue using the test statistic.
What is Test statistic?(A) A statistic (a quantity obtained from the sample) used in statistical hypothesis testing is known as a test statistic.
A test statistic, which can be thought of as a numerical summary of a data set that condenses the data into a single value that can be used to conduct the hypothesis test, is how a hypothesis test is commonly expressed.
In general, a test statistic is chosen or defined in a way that quantifies, within observed data, behaviors that would separate the null from the alternative hypothesis, where such an alternative is prescribed, or that would characterize the null hypothesis if there isn't an explicitly stated alternative hypothesis.
(B) Weakly positive association, r = 0.423.
(C) df = n-2 = 25-2 = 23 One-tailed Critical Value: = 0.05 T = 1.319
T, the test statistic, is defined as r*Sqrt[(n-2)/(1-r2)] = 0.423*Sqrt[(25-2)/(1-0.4232)]. = 2.24
We can infer that there is a positive link between the variables because 2.24 > 1.319.
(D) The variation in the number of rooms occupied accounts for around 18% of the variation in revenue, according to the formula r2 = 0.4232 = 0.179.
Therefore, attached is a plot that compares the two variables, income and revenue using the test statistic.
Know more about Test statistics here:
https://brainly.com/question/4621112
#SPJ4

Express the answers to the following operations with the proper number of significant figures. (a) 8.370×1.3 ×10 (b) 4.265/2.0 (c) (1.2588×10 ^3)×(1.06×10 ^−2) (d) (1.11) ^1/2
Answers
The answers, rounded to the appropriate number of significant figures, are as follows:
(a) 1.088 ×\(10^2\)
(b) 2.132
(c) 1.3331 ×\(10^1\) and
(d) 1.05.
Let's calculate the answers to the given operations using the appropriate number of significant figures.
(a) 8.370×1.3×10
To perform this multiplication, we multiply the decimal numbers and add the exponents of 10:
8.370 × 1.3 × 10 = 10.881 × 10 = 1.0881 × \(10^2\)
Since the original numbers have four significant figures, we round the final answer to four significant figures:
1.088 × \(10^2\)
(b) 4.265/2.0
For division, we divide the decimal numbers:
4.265 ÷ 2.0 = 2.1325
Since both numbers have four significant figures, the answer should be rounded to four significant figures:
2.132
(c) (1.2588×\(10^3\))×(1.06×\(10^-^2\))
To multiply these numbers, we multiply the decimal numbers and add the exponents:
(1.2588 × \(10^3\)) × (1.06 × \(10^-^2\)) = 1.333128 × \(10^1\)
Since the original numbers have five significant figures, we round the final answer to five significant figures:
1.3331 × \(10^1\)
(d) \((1.11)^(^1^/^2^)\)
To calculate the square root, we raise the number to the power of 1/2:
\((1.11)^(^1^/^2^)\)= 1.0524
Since the original number has three significant figures, the answer should be rounded to three significant figures:
1.05
It's important to note that the significant figures in a result are determined by the original data and the operations performed. The final answers provided above reflect the appropriate number of significant figures based on the given information and the rules for significant figures.
For more such information on: significant figures
https://brainly.com/question/30169
#SPJ8
