Answers
ANSWER
M=(−3,72)
Find A midpoint calculator on the internet
Related Questions
The probability distribution for a
random variable x is given in the table.
-5
-3
-2
2
3
Probability
.17
.13
.33
.16
.11
.10
Find the probability that x <= -3
Answers
Explanation:
Add up the probability values that correspond to x = -3 or smaller.
We'll add up the probability values corresponding to P(-3) and P(-5)
0.13+0.17 = 0.30
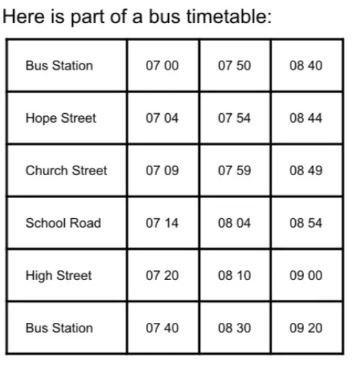
Here is part of a bus timetable:
Bus Station
a)
07 00
07 50
08 40
A bus leaves Hope Street at
07 54. What time should it
arrive at School Road?
Hope Street
07 04
07 54
08 44
b)
Church Street
07 09
07 59
08 49
Jo's school is on School Road.
Jo needs to get there at 8am.
What is the time of the latest
bus that she can catch from
the bus station?
School Road
07 14
08 04
08 54
High Street
07 20
08 10
09 00
c) How long does the bus take to
travel from the bus station to
School Road?
Bus Station
07 40
08 30
09 20
Answers
The time the bus should arrive at School Road from Hope Street is 08 : 04.
The time of the latest bus that Jo can catch from the Bus Station is 07 00.
The time the bus takes to travel from the bus station to School Road is 14 minutes.
How to find the time ?The table shows that when a bus leaves for School Road from Hope Street, at 07 54, it will arrive on School Road at 08 04.
The time it takes from the bus station to School road is:
= Arrival time at school road - Departure time from Bus station
= 08 04 - 07 50
= 14 minutes
If Jo wants to be in school road at 8 am by the latest, she needs to leave before :
= 8 am - 14 minutes
= 07 46
The only bus leaving before this time is the 0700 bus from the Bus Station.
Find out more on bus stations at https://brainly.com/question/13209100
#SPJ1
3) Are the following points part of the (200) plane? a) (1/2, 0, 0); b) (-1/3, 0, 0); c) (0, 1, 0)
Answers
To determine if the given points are part of the (200) plane, we need to check if their coordinates satisfy the equation of the plane.
The equation of a plane in three-dimensional space is typically written in the form Ax + By + Cz + D = 0, where A, B, C, and D are constants. For the (200) plane, the equation would be 2x + 0y + 0z + 0 = 0, which simplifies to 2x = 0. Let's check the given points: a) (1/2, 0, 0): When we substitute x = 1/2 into the equation 2x = 0, we get 2(1/2) = 0, which is true. Therefore, point a) lies on the (200) plane. b) (-1/3, 0, 0): Substituting x = -1/3 into the equation 2x = 0 gives us 2(-1/3) = 0, which is also true. So, point b) is part of the (200) plane. c) (0, 1, 0):When we substitute x = 0 into the equation 2x = 0, we get 2(0) = 0, which is true. Thus, point c) lies on the (200) plane. All three given points (a), b), and c)) are part of the (200) plane.
In conclusion, all three given points (a), b), and c)) are part of the (200) plane.
To learn more about equation of the plane click here: brainly.com/question/27190150
#SPJ11
how many miles will be remaining after 59 minutes of driving

Answers
The graph depicts a linear relationship between her driving time (x variable) and the remaining distance (y variable). Knowing that this is a linear relationship, we can represent it as a equation in the slope intercept form. This is because we already have the slope as -0.9.
Therefore we would have the following;
\(\begin{gathered} y=mx+b \\ \text{Where;} \\ x=47,y=41,m=-0.9 \end{gathered}\)We can now substitute the given variables into the equation in slope-intercept form as follows;
\(\begin{gathered} y=mx+b \\ 41=-0.9(47)+b \\ 41=-42.3+b \\ \text{Add 42.3 to both sides;} \\ 41+42.3=-42.3+42.3+b \\ 83.3=b \\ \text{The equation therefore becomes;} \\ y=-0.9x+83.3 \end{gathered}\)With the equation for the graph now determined, we shall find the mileage after 59 minutes of driving as follows;
\(\begin{gathered} \text{After 53 minutes of driving (x),} \\ \text{The miles remaining (y) shall be;} \\ y=-0.9x+83.3 \\ y=-0.9(53)+83.3 \\ y=-47.7+83.3 \\ y=35.6 \end{gathered}\)ANSWER:
After 59 minutes of driving, she would have 35.6 miles remaining.
ILL GIVE BRAINIEST TO WHOEVER IS CORRECT!! PLEASE HELP ASAP!!

Answers
Answer:
1. -1/2x+ 11.5
2. -1/3x-8.7
Step-by-step explanation:
Answer:
Step-by-step explanation:


ILL GIVE BRAINLIST IF ITS CORRECT PLEASE HELP ASAP!!

Answers
Answer:
check the attachment and explanation below
Step-by-step explanation:
Explanation for statement 3 :
Suppose The number of shoppers on Saturday is 100 and the number of shoppers on Sunday is 200
Total number of shoppers = 300
On Saturday :
Q₃ = 70 then 25% of shoppers spent more then $70
then 25 shopper spent more then $70
On Sunday:
M’ = 70 then 50% of shoppers spent more then $70
then 100 shopper spent more then $70
On both days:
(100+ 25) shopper spent more then $70
Then 125 shopper spent more then $70
But 125 is not 75% of 100+200=300

Replace the values of h and k to create the equation of the transformed function.

Answers
Answer:
h = 4 and k = 1Step-by-step explanation:
y = ∛x is the original function, which has its center in the origin
As we see the function y = ∛(x - h) - x has its center moved to the point (4, -1)
This gives us h = 4 and k = 1, as negative h indicates translation to the right and negative k- translation down

Add or subtract -1+(-3)
Answers
Answer:
It owuld be -2
Step-by-step explanation:
Yes
Find the value of x.
-2(6x - 3) = 27
Answers
Answer:
x = -7/4Step-by-step Solution:
Let's simplify the equation to find the value of x.
-2(6x - 3) = 27[Simplify the Distributive property]
=> -12x + 6 = 27[Subtract 6 both sides]
=> -12x = 27 - 6[Solve the RHS]
=> -12x = 21[Divide -12 both sides to isolate the variable]
=> x = -21/12[Simplify the fraction]
=> x = -7/4Hence, the value of x is -7/4.
Answer:
x = -1.75
Step-by-step explanation:
-2(6x - 3) = 27
distribute the -2
-2 * 6x = -12x
-2 * -3 = 6
-12x + 6 = 27
subtract 6 from both sides
-12x = 21
divide both sides by -12
-12x/-12 = x
21/-12 = -1.75
we're left with x = -1.75
SOLVE THE FOLLOWING PROBLEMS SHOWING EVERY DETAIL OF YOUR
SOLUTION. ENCLOSE FINAL ANSWERS.
7. Particular solution of (D³ + 12 D² + 36 D)y = 0, when x = 0, y = 0, y' = 1, y" = -7 8. The general solution of y" + 4y = 3 sin 2x 9. The general solution of y" + y = cos²x 10. Particular solutio
Answers
(8) To find the particular solution of (D³ + 12D² + 36D)y = 0 with initial conditions x = 0, y = 0, y' = 1, y" = -7, we can assume a particular solution of the form y = ax³ + bx² + cx + d.
Taking the derivatives:
y' = 3ax² + 2bx + c
y" = 6ax + 2b
Substituting these derivatives into the differential equation, we get:
(6ax + 2b) + 12(3ax² + 2bx + c) + 36(ax³ + bx² + cx + d) = 0
36ax³ + (72b + 36c)x² + (36a + 24b + 36d)x + (2b + 6c) = 0
Comparing coefficients of like powers of x, we can set up a system of equations:
36a = 0 (coefficient of x³ term)
72b + 36c = 0 (coefficient of x² term)
36a + 24b + 36d = 0 (coefficient of x term)
2b + 6c = 0 (constant term)
From the first equation, we have a = 0. We get:
72b + 36c = 0
24b + 36d = 0
2b + 6c = 0
Solving this system of equations, we find b = 0, c = 0, and d = 0. Therefore, the particular solution of (D³ + 12D² + 36D)y = 0 with the given initial conditions is y = 0.
(9) The general solution of y" + 4y = 3sin(2x) is given by y = C₁cos(2x) + C₂sin(2x) - (3/4)cos(2x), where C₁ and C₂ are arbitrary constants.
(10) To find the particular solution of y" + y = cos²x, we can use the method of undetermined coefficients. We can assume a particular solution of the form y = Acos²x + Bsin²x + Ccosx + Dsinx, where A, B, C, and D are constants.
Taking the derivatives:
y' = -2Acosxsinx + 2Bcosxsinx - Csinx + Dcosx
y" = -2A(cos²x - sin²x) + 2B(cos²x - sin²x) - Ccosx - Dsinx
Substituting these derivatives into the differential equation, we get:
(-2A(cos²x - sin²x) + 2B(cos²x - sin²x) - Ccosx - Dsinx) + (Acos²x + Bsin²x + Ccosx + Dsinx) = cos²x
-2Acos²x + 2Asin²x + 2Bcos²x - 2Bsin²x - Ccosx - Dsinx + Acos²x + Bsin²x + Ccosx + Dsinx = cos²x
(-A + B + 1)cos²x + (A - B)sin²x - Ccosx - Dsinx = cos²x
Comparing coefficients of like powers of x, we can set up a system of equations:
-A + B + 1 = 1 (coefficient of cos²x term)
A - B = 0 (coefficient of sin²x term)
-C = 0 (coefficient of cosx term)
-D = 0 (coefficient of sinx term)
From the second equation, we have A = B. Substituting this into the remaining equations, we get:
-A + A + 1 = 1
-C = 0
-D = 0
Simplifying further, we have:
1 = 1, C = 0, and D = 0
From the first equation, we have A - A + 1 = 1, which is true for any value of A. Therefore, the particular solution of y" + y = cos²x is y = Acos²x + Asin²x, where A is an arbitrary constant.
To know more about differential equation refer here:
https://brainly.com/question/31492438#
#SPJ11
please help me slove these problems!! offering 30 points for good answers and explanation on it




Answers
here's two, I used mathday but day with a w
Step-by-step explanation:
good website for it and it gives good explanation! Gl


Someone please help me with this!!!

Answers
Step-by-step explanation:
what, you have no calculator at hand ? at least the computer or smart phone you used to pay this question has one installed.
because this is all that needs to be done : use the given numbers and just calculate the results for every expression.
sigh ...
a.
2²×-3 = 4×-3 = -12
b.
6×(2-4)/-3 = 6×-2/-3 = -2×-2 = 4
c.
(-3)² + 2×4 = 9 + 8 = 17
d.
-(-3)² + 2 + 4 = -9 + 6 = -3
e.
-2×(-3 + 2×4)/-3 = -2×(-3 + 8)/-3 = -2×5/-3 = -10/-3 = 10/3
A salon owner noted what types of services its clients requested last week. Here are the results:
Dye
Haircut
Permanent
5% 30%
10% 5%
2NE
STA
35%
15%
In this sample, are the events "dye" and "permanent mutually exclusive?
MY
Choose
answer
Cor
Yes
MY
No
Pro
Pro
Find the probability that a randomly selected person from this sample requested a dye OR a permanent.
Tel
P(dye OR permanent) =

Answers
Answer:
5%+30%+10%+5%=50%
Step-by-step explanation:

There is no intersection between the two sets dye and permanent so it means both sets don't have any common thus both will be mutually exclusive events therefore, option (A) will be correct.
What is a set?A set is a combination of specific quantities in which the meaning of each variable must be the same.
For example set of names starting with A is {Amesh, Aniket, Aakash}
Sets of natural number {1,2,3,4,5....}
As per the given venn diagram,
The sets or events are dye haircuts and permanent.
The mutually exclusive are the events among them nothing have in common.
For example, the set of positive numbers {1,2,3} and the set of negative numbers {-1,-2,-3} now among both sets nothing is common so they will be exclusive events.
Since the intersection area in the Venn diagram represents the common things and among Dye and Permanent, no intersection area is formed thus they will be mutually exclusive events.
Hence "There is no intersection between the two sets dye and permanent so it means both sets don't have any common thus both will be mutually exclusive events".
To learn more about the sets,
brainly.com/question/8053622
#SPJ5
What is the slope of a line that contains the points (-4,-8) and (2,-2)
Answers
Answer:
1
Step-by-step explanation:
Slope is given by
m = (y2 -y1)/(x2-x1)
= ( -2 - -8)/( 2 - -4)
=( -2+8) / (2+4)
=6/6
=1
Answer:
\(\displaystyle m = 1\)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Coordinates (x, y)Slope Formula: \(\displaystyle m = \frac{y_2-y_1}{x_2-x_1}\)Step-by-step explanation:
Step 1: Define
Identify
Point (-4, -8)
Point (2, -2)
Step 2: Find slope m
Simply plug in the 2 coordinates into the slope formula to find slope m
Substitute in points [Slope Formula]: \(\displaystyle m = \frac{-2--8}{2--4}\)[Fraction] Subtract: \(\displaystyle m = \frac{6}{6}\)[Fraction] Divide: \(\displaystyle m = 1\)(25 points) Find two linearly independent solutions of 2x²y" – my' +(1:2 +1)y=0, x > 0 of the form yı = 2"(1+212 + a22² +2323 + ...) Y2 = 2" (1 + b2x + b222 + b3x3 + ...) where rı > 12 Enter Ti=
Answers
Two linearly independent solutions of 2x²y" – my' +(1:2 +1)y=0, x > 0 of the form yı = 2"(1+212 + a22² +2323 + ...) Y2 = 2" (1 + b2x + b222 + b3x3 + ...) where rı > 12 are y₁ = x^(-1/2) Σ(n=0 to ∞) (1/2^n) [(m+2n-2)/Γ(n+1/2)] and y₂ = x^(-1/2) Σ(n=0 to ∞) (1/2^n) [(m+2n-2)/(2n+1)Γ(n+3/2)], using the method of Frobenius.
To find linearly independent solutions of the given differential equation, we can use the method of Frobenius. For this, we assume the solutions to have the form:
y = x^r Σ(n=0 to ∞) a_n x^n
Substituting this form into the differential equation, we get:
2x^2 Σ(n=0 to ∞) [(r+n)(r+n-1)a_n x^(n+r-2)] - m Σ(n=0 to ∞) [(r+n)a_n x^(n+r-1)] + (2+r^2+2r) Σ(n=0 to ∞) [a_n x^(n+r)] = 0
Equating the coefficient of x^(r-2), we get:
2r(r-1)a_0 = 0
Since x>0, we can assume r>0, and hence a_0 = 0. Equating the coefficient of x^r, we get:
2r^2 + 2r + 1 = 0
Solving for r using the quadratic formula, we get:
r = (-1 ± √3 i)/2
These are complex roots, and hence we can use the following forms for the solutions:
y₁ = x^r Σ(n=0 to ∞) a_n x^(n+r) = x^(-1/2) Σ(n=0 to ∞) a_n x^n
y₂ = x^r Σ(n=0 to ∞) b_n x^(n+r) = x^(-1/2) Σ(n=0 to ∞) b_n x^n
Now, substituting the forms of y₁ and y₂ into the differential equation and equating the coefficients of x^n, we get:
[2(n+r+1)(n+r)a_n - m(n+r)a_n + (2+r^2+2r)a_n] + [2(n+r+1)(n+r)b_n - m(n+r)b_n + (2+r^2+2r)b_n] = 0
Simplifying the expression, we get two recurrence relations:
a_n+1 = [(m-2r-2n-1)/(2r+2n+2)] a_n
b_n+1 = [(m-2r-2n-1)/(2r+2n+2)] b_n
Using these recurrence relations, we can find the coefficients a_n and b_n in terms of a_0 and b_0.
Since we want two linearly independent solutions, we can choose different values of a_0 and b_0. One possible choice is a_0 = 1 and b_0 = 0, which gives:
y₁ = x^(-1/2) Σ(n=0 to ∞) (1/2^n) [(m+2n-2)/Γ(n+1/2)]
y₂ = 0
where Γ is the gamma function. Another possible choice is a_0 = 0 and b_0 = 1, which gives:
y₁ = 0
y₂ = x^(-1/2) Σ(n=0 to ∞) (1/2^n) [(m+2n-2)/(2n+1)Γ(n+3/2)]
Therefore, two linearly independent solutions of the given differential equation are:
y₁ = x^(-1/2) Σ(n=0 to ∞) (1/2^n) [(m+2n-2)/Γ(n+1/2)]
y₂ = x^(-1/2) Σ(n=0 to ∞) (1/2^n) [(m+2n-2)/(2n+1)Γ(n+3/2)]
To know more about linearly independent solutions refer here:
https://brainly.com/question/31961716#
#SPJ11
How are cubic functions similar to linear functions? How are
they different?
Answers
The cubic functions and linear functions, both are polynomial having degree of 3 and 1 respectively.
Define the cubic functions and linear functions?One of the key ideas in mathematics is the concept of polynomials, along with the multiple sorts of polynomials that can be created depending on the degree for polynomials.
When a variable's largest exponent is one, a polynomial with degree one is said to be linear. This type of polynomial is denoted by the equation p(x): ax + b, a≠0.A cubic polynomial is a three-degree polynomial, meaning that three is the largest exponent of the variable. In general, a cubic polynomial will have the following form: p(x): ax³ + bx² + cx + d, a≠0.Some properties of cubic functions and linear functions are-
An n-degree polynomial will have n zeros or roots.Every number of terms, however never an infinite number, can exist in a polynomial.Expressions are represented by zeros, while equations are represented by roots.To know more about the cubic functions and linear functions, here
https://brainly.com/question/20896994
#SPJ1
The sum of three consecutive integers is 105. Find the integers.
Answers
Answer:
34,35,and 36
Step-by-step explanation:
x+x+1+x+2=105
3x+3=105 combine like terms on the left side
3x=102 subtract three on both sides
x=34 divide by three on both sides.
Hope this helps plz mark brainliest :D
Log_6 x + log_6 3 = log_6 (x+1)
Answers
The solution to the equation log_6 x + log_6 3 = log_6 (x+1) is x = 1/2.
Explain:
We can reduce the complexity of the left side of the equation by using the logarithmic identity log a + log b = log (ab):
Log6 x plus Log6 3 equals Log6 (3x)
When we add this to the initial equation, we obtain:
Log6 (3x) equals Log6 (x+1).
Because logarithms have the one-to-one property, we can drop the logarithm on both sides to get the following results:
3x = x + 1
When we simplify this equation, we obtain:
2x = 1
x = 1/2
As a result, x = 1/2 is the answer to the equation log 6 x + log 6 3 = log 6 (x+1).
To know more about Logarithmic visit:
https://brainly.com/question/20835449
#SPJ1
in a class of 29 students, 18 of them like maths 12 of them like english and 7 of them dont like maths or english find the probability that a student chosen at random likes maths but not english
Answers
Answer:
18/29
Step-by-step explanation:
(p like math) = 18/29
Answer:
17/29
Step-by-step explanation:
We must take into account the amount of students who prefer math over English in order to calculate the probability that a student selected at random like arithmetic but dislikes English.
Let's denote:
X = Number of students who like math = 18 students
Y = Number of students who like English = 12 students
Z = Number of students who don't like math or English = 7 students
We can calculate the number of students who like both math and English using the principle of inclusion-exclusion:
Therefore , Number of students who like both math and English = X + Y - (X ∩ Y)
= 18 + 12 - (Total number of students in the class)
= 18 + 12 - 29
= 1
Now, the probability of selecting a student who likes math but not English is the ratio of the number of students who like math but not English to the total number of students in the class:
Therefore, Probability = Number of students who like math but not English / Total number of students
= 17 / 29
Therefore, the probability that a student chosen at random likes math but not English is 17/29.
To learn more about inclusion-exclusion principle in probability:
https://brainly.com/question/32375490?referrer=searchResults
36 flowers in 3 bouquets
This is called the unit rate.
Answers
Answer: Yes, you are correct.
Step-by-step explanation:
The relationship between the number of flowers and the number of bouquets is an example of a unit rate.
Answer:
yes
Step-by-step explanation:
it is a unit rate
evaluate the expression x= 2/5y = 5/12\( - 3y + x\)
![evaluate the expression x= 2/5y = 5/12[tex] - 3y + x[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/vYjrC0rfNp4JQM0dViCSGr8c2o6oEdiC.png)
Answers
Given :
It is given that
\(x=\frac{2}{5},y=\frac{5}{12}\)To find
\(-3y+x\)Explanation
In the given equation , substitute the value of x and y .
\(-3\times\frac{5}{12}+\frac{2}{5}=-\frac{5}{4}+\frac{2}{5}\)\(-\frac{5}{4}+\frac{2}{5}=\frac{-25+8}{20}=-\frac{17}{20}\)Answer
Hence the answer in simplest form is
\(-\frac{17}{20}\)the set of all elements of interest in a study is . a. a sample b. set notation c. a set of interest
Answers
The statement describes a set of interest in a study, which is the set of all elements being investigated or under consideration. It is not a sample, which refers to a subset of the population being studied.
The set of all elements of interest in a study is called the population. It refers to the entire group of individuals, objects, or measurements that are being studied and from which data can be collected. The population can be finite or infinite and can include people, animals, plants, materials, or any other object or concept of interest. In statistical analysis, researchers use samples of the population to make inferences or draw conclusions about the entire population. By selecting a representative sample, researchers can reduce the cost and time required for data collection and analysis while still obtaining valid and reliable results.
Learn more about statistics here: brainly.com/question/29093686
#SPJ1
Multiply 3 • (-8) • (-2)
Answers
Step-by-step solution:-
3 * (-8) * (-2)
= -24 * (-2)
= 48 ... (minus * minus = +)
Manny saves coins in a jar. He counts his dimes and has $16. How many dimes does Manny have?
Answers
First, multiply 16 by 100, then divide that result by 10 cents.
$16 x 100 cents
= 1,600 cents
1,600 cents / 10 cents
= 160 dimes
If you are given three lengths of wood at 5 feet, 8 feet and 9 feet to form the perimeter of a triangular garden, what type of triangle will be formed?
Answers
It will form scalene triangle
because it has different measures of sides
that is no equal side
may thishelps you
byr
A university professor does not believe that there is really a difference between the GPA of male and female scholarship athletes, so he looks into how the sample was collected. His investigation shows that the study was given to all of the athletes on the basketball teams exclusively. Based on this information, should the university administration trust the results from this study?
a. Yes, because the results were significant
b. Yes, because a large enough sample was taken
c. No, because not every scholarship athlete part of the study
d. No, because the study was not taken from a random sample of scholarship athletes
Answers
Answer: d. No, because the study was not taken from a random sample of scholarship athletes.
Step-by-step explanation:
Since the study only focuses on basketball players, the sample may not be representative of all scholarship athletes in the university. This can cause bias in the results and make it difficult to generalize the findings to the larger population of scholarship athletes. Therefore, the university administration should not fully trust the results of this study.
Show that (n + 3)7 ∈ Θ(n7) for
non-negative integer n.
Proof:
Answers
To show that `(n + 3)7 ∈ Θ(n7)`, we need to prove that `(n + 3)7 = Θ(n7)`.This can be done by showing that `(n + 3)7 = O(n7)` and `(n + 3)7 = Ω(n7)` .Now, let's prove the two parts separately:
Proof for `(n + 3)7 = O(n7)`.
We want to prove that there exists a positive constant c and a non-negative constant k such that `(n + 3)7 ≤ cn7` for all `n ≥ k`.Using the Binomial theorem, we can expand `(n + 3)7` as:```
(n + 3)7
= n7 + 7n6(3) + 21n5(3)2 + 35n4(3)3 + 35n3(3)4 + 21n2(3)5 + 7n(3)6 + 37
≤ n7 + 21n6(3) + 21n5(3)2 + 35n4(3)3 + 35n3(3)4 + 21n2(3)5 + 7n(3)6 + n7
≤ 2n7 + 21n6(3) + 21n5(3)2 + 35n4(3)3 + 35n3(3)4 + 21n2(3)5 + 7n(3)6
≤ 2n7 + 84n6 + 441n5 + 2205n4 + 10395n3 + 45045n2 + 153609n + 729
```Thus, we can take `c = 153610` and `k = 1` to satisfy the definition of big-Oh notation. Hence, `(n + 3)7 = O(n7)`.Proof for `(n + 3)7 = Ω(n7)`We want to prove that there exists a positive constant c and a non-negative constant k such that `(n + 3)7 ≥ cn7` for all `n ≥ k`.Using the Binomial theorem, we can expand `(n + 3)7` as:```
(n + 3)7
= n7 + 7n6(3) + 21n5(3)2 + 35n4(3)3 + 35n3(3)4 + 21n2(3)5 + 7n(3)6 + 37
≥ n7
```Thus, we can take `c = 1` and `k = 1` to satisfy the definition of big-Omega notation. Hence, `(n + 3)7 = Ω(n7)`.
As we have proved that `(n + 3)7 = O(n7)` and `(n + 3)7 = Ω(n7)`, therefore `(n + 3)7 = Θ(n7)`.Thus, we have shown that `(n + 3)7 ∈ Θ(n7)`.From the proof, we can see that we used the Binomial theorem to expand `(n + 3)7` and used algebraic manipulation to bound it from above and below with suitable constants. This technique can be used to prove the time complexity of various algorithms, where we have to find the tightest possible upper and lower bounds on the number of operations performed by the algorithm.
Hence, we have shown that `(n + 3)7 ∈ Θ(n7)` for non-negative integer n.
To know more about Binomial theorem :
brainly.com/question/30095070
#SPJ11
find the area of each square. each grid square represents square unit. use the sketch tool if it helps you with your thinking.
Answers
The area of the squares are
A = 17 units², B = 20 units², C = 13 units², and D = 37 units²
Finding area using grid paper
Count the number of complete squares that are fully contained within the shape. Start from one corner of the shape and count each square until you reach the opposite corner. Include any partial squares as well.
If there are partial squares, estimate the area they cover. You can do this by visualizing how much of each square is filled by the shape and approximate the area accordingly.
Add up the areas of the complete squares and the estimated areas of the partial squares to find the total area of the shape.
Here we have 4 squares A, B, C, and D
Now count the number of unit squares covered by each square
Number of squares covered by A = 17
Hence, the Area of Square A = 17 units²
Number of squares covered by B = 20
Hence, the Area of square B = 20 units²
Number of squares covered by C = 13
Hence, the Area of square C = 13 units²
Number of squares covered by D = 37
Hence, the Area of square D = 37 units²
Therefore,
The area of the squares are
A = 17 units², B = 20 units², C = 13 units², and D = 37 units²
Learn more about Area at
https://brainly.com/question/19581847
#SPJ4
Complete Question is attached below

Without graphing, identify the equations of the lines that are (a) parallel and (b) perpendicular. Explain your reasoning. HELP ASAP LIKE LITE ASAP OML PLEASE


Answers
Answer:
b) \(y = -3x - 2\) and \(y = -3x + 5\) are parallel because the slope of each line is -3
can any one help me please I need Complete information / details about the solution

Answers
\( \huge \boxed{\mathbb{QUESTION} \downarrow}\)
Answer the 2 questions.\( \large \boxed{\mathfrak{Answer \: with \: Explanation} \downarrow}\)
1st Question :-a) State what's asked to find \(\downarrow\)
the length of the rectangular garden.b) State the given facts \(\downarrow\)
area of a rectangular pool (garden) = x² + x - 12 cm²width of the garden = x + 4 cm.c) Write a working equation \(\downarrow\)
area of the garden = length of the garden × width of the garden. Let's take the length as 'l'. So the equation is...
x² + x - 12 = l × (x + 4)d) Solve the equation \(\downarrow\)
\( \tt {x}^{2} + x - 12 = l \times (x + 4) \\ \\ \sf \: Bring \: (x + 4) \: towards \: the \: left \: side \\ \sf\: of \: the \: equation. \\ \\ \tt \frac{ {x}^{2} + x - 12 }{x + 4} = l \\ \\ \sf \: Factor \: the \: expressions \: that \: are \\ \sf \: not \: already \: factored. \\ \\ \tt \frac{\left(x-3\right)\left(x+4\right)}{(x+4)} = l\\ \\ \sf Cancel \: out \: (x + 4) \: in \: both \: the \\ \sf \: numerator \: and \: denominator. \\ \\ \large \boxed{\boxed{ \bf \: (x-3 )= l}}\)
e) State your answer \(\downarrow\)
The length of the rectangular garden is x - 3 cm.NOTE :-I think there's a mistake in the question. It should be the area of the rectangular garden & not area of the rectangular pool because here we are asked to measure the length of the garden.
__________________
2nd Question :-a) State what's asked to find \(\downarrow\)
the length of the side of the square.b) State the given facts \(\downarrow\)
area of the tile = x² + 10x + 25 cm²c) Write a working equation.
We know that, area of a square = side of the square × side of the square. Let's take the side of the tile (square) as 's'. So, the equation is...
x² + 10x + 25 = s × sd) Solve the equation \(\downarrow\)
\( \tt {x}^{2} + 10x + 25 = s \times s \\ \\ \sf \: s \: \times \: s \: is \: equal \: to \: {s}^{2} \\ \\ \tt \: {x}^{2} + 10x + 25 = {s}^{2} \\ \\ \sf \: Using \: split \: the \: middle \: term \: method.. \\ \\ \tt \: {x}^{2} + 10x + 25 = {s}^{2} \\ \tt \: \left(x^{2}+5x\right)+\left(5x+25\right) = {s}^{2} \\ \tt x\left(x+5\right)+5\left(x+5\right) = {s}^{2} \\ \tt \: \left(x+5\right)\left(x+5\right) = {s}^{2} \\ \tt\left(x+5\right)^{2} = {s}^{2} \\ \\ \sf \: Now \: squaring \: on \: both \: the \: sides.. \\ \\ \tt \: \sqrt{(x + 5) ^{2} } = \sqrt{ {s}^{2} } \\ \large \boxed{\boxed{ \bf \: (x + 5) = s}}\)
e) State your answer \(\downarrow\)
The length of 1 side of the square is x + 5 cm.__________________
