Answers
Answer:
Step-by-step explanation:
c
Answer:
na saan Po yong question
Related Questions
experimental designs with are called independent-measures designs. experimental designs with are called repeated-measures designs.
Answers
Independent-measures designs, also known as between-subjects designs, involve comparing two or more separate groups of participants. Each group is exposed to a different experimental condition or treatment.
The main advantage of this design is that it eliminates the possibility of practice effects or carryover effects, as each participant is only exposed to one condition.
On the other hand, repeated-measures designs, also known as within-subjects designs, involve testing the same group of participants under all experimental conditions. This design has the advantage of requiring fewer participants, as each person serves as their own control. Additionally, it reduces variability between participants, allowing for a more sensitive analysis of the experimental effects.However, repeated-measures designs can be susceptible to practice effects or carryover effects, as participants may improve or become fatigued after repeated testing. Counterbalancing techniques are often employed to minimize these effects.In summary, independent-measures designs involve testing separate groups of participants in different experimental conditions, while repeated-measures designs test the same group of participants under all conditions.Know more about the variability
https://brainly.com/question/12872866
#SPJ11
Pls halp due today >_<. Thank you

Answers
Answer: A. -6.007, -2π, -√48
Step-by-step explanation:
-2π ≈ -6.28
-√48 ≈ -6.93
-6.007 = -6.007
-----------------------
-6.007>-6.28>-6.93
-6.007>-2π>-√48
Hope this will help you.
HELP MEEEEEEEEEEEEEEEE PLEASEEEEEEEEEEEE!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
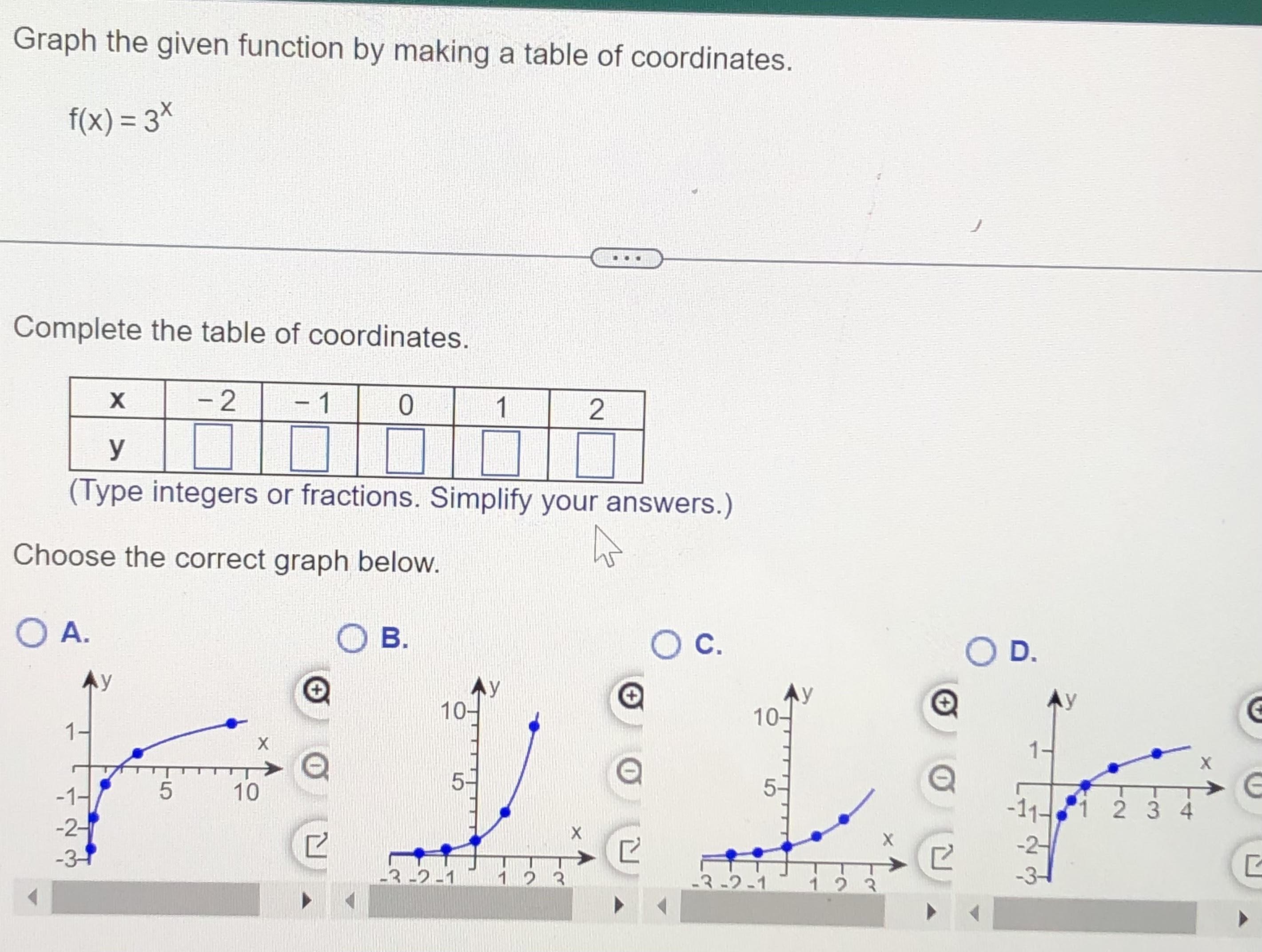
Answers
Answer:
x = -2, y = (1/9)
x = -1, y = (1/3)
x = 0, y = 1
x = 1, y = 3
x = 2, y = 9
Graph B
Step-by-step explanation:
f(x) = 3ˣ
y = 3ˣ
1
y = 3⁽⁻²⁾ = ------
9
1
y = 3⁽⁻¹⁾ = -------
3
y = 3⁽⁰⁾ = 1
y = 3⁽¹⁾ = 3
y = 3⁽²⁾ = 9
I hope this helps!
The areaot a square is 36 cm? What
is the side length, s?
Answers
Answer: 6
Step-by-step explanation: To find the side length of a square, you need to find the square root of the area because the side length squared is the area.
Find the y-intercept of the parabola y = x2 + 3x.
Answers
Answer:
(0,0)
Step-by-step explanation:
The y-intercept is where the parabola crosses the y-axis. The y-intercept is expressed as a coordinate pair, where x is always equal to 0 because the y-axis exists where x=0.
There are 2 ways to find the y-intercept of a function. The first way is to plug in 0 for x because you know that x=0 at the y-intercept. Then, solve for y.
First, plug-in 0 for x\(y=0^2+3(0)\)
Then, simplify the equationy=0
Since y=0, the y-value of the intercept is 0. Thus making the y-intercept (0,0).The second, and easier, way to find the y-intercept is to use logic. Since you are plugging in 0 for x, all terms that have variables will equal 0. This means that all that is left are the constants. So, the easiest way to find the y-intercept is to just simplify the constants. Whatever this equals will be the y-value of the y-intercept. Since there are no constants written in this equation, the constant must be 0. If 0 is the constant, then that must mean that the y-value of the intercept is 0.
Which of the following is a parent function?

Answers
Answer:
B
Step-by-step explanation:
A parent function is the simplest function that still satisfies the definition of a certain type of function. One of those functions is exponential, which is b.
Option (B) will be the correct option.
Definition of a parent function:A parent function is simplest function which represents the entire family of that kind of functions.
We will check each option given for the definition of a parent function.
Option (A)
\(f(x)=-2^{x+1}\)
Parent function will be,
\(f(x)=2^x\)
Option (B),
\(f(x)=4^x\)
It's a simplest form of an exponential function.
Therefore, it's a parent function.
Option (C),
\(f(x)=e^{3x}-2\)
Parent function → \(f(x)=e^{3x}\)
Option (D),
\(f(x)=4x^2\)
Parent function → \(f(x)=x^2\)
Learn more about the parent function and the transformation here,
https://brainly.com/question/11474649?referrer=searchResults
Find the range for the given domain: {-2, -1, and 0} and the function is y = 3x2.
Answers
The range of the function at domain {-2, -1, and 0} will be { 12 , 3 and 0}.
What is range?
A function's range is the collection of values it can take as input. After we enter an x value, the function outputs this sequence of values.
Given that:-
The range for the given domain: {-2, -1, and 0} and the function is y = 3x².
The range will be the value of y at each given value of the domain.
Domain: { -2, -1, 0 }
y = 3x²
At x = -2 → y = 3 ( -2)² = 12
At x = -1 → y = 3 (-1)² = 3
At x = 0 → y = 3 (0) = 0
Therefore range of the function at domain {-2, -1, and 0} will be { 12 , 3 and 0}.
To know more about Range follow
brainly.com/question/26098895
#SPJ1
The coordinates of the endpoints of MP are M(-3,-2) and P(-2,3). which measurement is closest to the length of MP in units
A 7.1 units
B 5 units
C 4.5 units
D 10 units
Answers
Answer: The answer is, A 7.1 units
Step-by-step explanation:
A farmer goes to the market to sell a box of eggs. A clumsy horse steps on the box of eggs and breaks a lot of them. The horse’s rider offers to pay for all of the eggs in the box and asks the farmer how many eggs there were. The farmer does not remember the exact number, but when she took them out of the box two at a time, there was 1 egg left. The same thing happened when she took them out three, four, five and six eggs at a time, but when she took them out 7 at a time, there were no eggs left
Answers
The smallest number of eggs that could have been in the box is 1134
The problem is to find the smallest number of eggs that could have been in the box, given the remainder when taking them out by different numbers. Here are the moves toward tackling it:
Allow n to be the quantity of eggs in the container. Then we have the accompanying arrangement of congruences:
n ≡ 1 (mod 2)
n ≡ 1 (mod 3)
n ≡ 1 (mod 4)
n ≡ 1 (mod 5)
n ≡ 1 (mod 6)
n ≡ 0 (mod 7)
For this problem, we have k = 6 k = 6, a i = {1,1,1,1,1,0} a_i = {1,1,1,1,1,0}, M i = {1260,840,630,504,420,720} M_i = {1260,840,630,504,420,720}, and y i = {−1,−2,−3,-4,-5,-6} y_i = {-1,-2,-3,-4,-5,-6}.
Plugging these values into the formula and simplifying modulo 5040, we get:
n = (−1260 + −1680 + −1890 + −2016 + −2100 + 0) mod 5040
n = (−8946) mod 5040
n = (−3906) mod 5040
n = 1134 mod 5040
Therefore, the smallest number of eggs that could have been in the box is 1134
to know more about congruences click here:
https://brainly.com/question/30818154
#SPJ4
a radio tower is located 350 feet from a building. from a window in the building, a person determines that the angle of elevation to the top of the tower is 42 degrees and that the angle of depression to the bottom of the tower is 28 degrees . how tall is the tower?
Answers
The height of the tower is approximately 336.4 feet. To find the height of the tower, we can use trigonometric ratios in a right triangle formed by the tower, the person's line of sight, and the ground.
Let's label the height of the tower as "h" in feet. We can divide the right triangle into two smaller triangles: one with the angle of elevation of 42 degrees and the other with the angle of depression of 28 degrees.
In the triangle with the angle of elevation, the side opposite the angle of elevation is the height of the tower, h, and the side adjacent to the angle of elevation is the distance from the window to the tower, which is 350 feet. We can use the tangent function to relate the angle of elevation and the sides of the triangle:
tan(42 degrees) = h / 350
Similarly, in the triangle with the angle of depression, the side opposite the angle of depression is also the height of the tower, h, and the side adjacent to the angle of depression is the distance from the window to the tower, which is still 350 feet. Using the tangent function again, we have:
tan(28 degrees) = h / 350
We can solve these two equations simultaneously to find the value of h. Rearranging the equations:
h = 350 * tan(42 degrees)
h = 350 * tan(28 degrees)
Evaluating these expressions, we find that h is approximately 336.4 feet.
Therefore, the height of the tower is approximately 336.4 feet.
Learn more about trigonometric ratios here:
https://brainly.com/question/23130410
#SPJ11
The sum of the digits of a 2-digit number is 12. The second digit is 6 more than the first digit. What was the original number
Answers
Step-by-step explanation:
lets take the first number as x
if the second digit is 6 more than the first, we should take it as x+6
if they add up to 12,then:
x+x+6 = 12
2x = 12 -6
2x = 6
x = 6/2=3
if the 1st digit is 3, then the 2nd will be 6+3=9
so the 2 digit number is 39
we wish to construct a rectangular auditorium with a stage shaped as a semicircle of radius $r$, as shown in the diagram below (white is the stage and green is the seating area). for safety reasons, light strips must be placed on the perimeter of the seating area. if we have $45\pi 60$ meters of light strips, what should $r$ be so that the seating area is maximized?
Answers
To maximize the seating area while using 45π + 60 meters of light strips, the radius of the semicircular stage should be approximately 29π/3 - 5 meters.
To maximize the seating area, we need to determine the dimensions of the rectangular auditorium that will give us the largest possible area while using the given length of light strips.
Let the length of the rectangular auditorium be L, and its width be W.
The seating area consists of the rectangular portion minus the semicircular stage. So, the seating area's length is L - 2r (subtracting the semicircle's diameter) and the seating area's width is W - 2r.
The perimeter of the seating area is the sum of the lengths of its four sides, excluding the semicircular stage. The perimeter is given as 45π + 60 meters.
Perimeter = 2(L - 2r) + 2(W - 2r) + πr = 45π + 60
Simplifying: 2L + 2W - 8r + πr = 45π + 60
Rearranging: 2L + 2W = 8r + 44π + 60
The area of the seating area is given by A = (L - 2r)(W - 2r).
We want to maximize A, so we need to express it in terms of a single variable. Since we have an equation with two variables (L and W), we can rewrite one of the variables in terms of the other.
Rearranging the perimeter equation: 2L + 2W = 8r + 44π + 60
Solving for L: L = (8r + 44π + 60 - 2W) / 2
Substituting L in terms of W into the area equation: A = [(8r + 44π + 60 - 2W) / 2 - 2r] (W - 2r)
Simplifying: A = (4r + 22π + 30 - W) (W - 2r)
Now we have the area equation in terms of a single variable, W. To maximize A, we can take the derivative of A with respect to W, set it equal to zero, and solve for W.
dA/dW = 2(4r + 22π + 30 - W) - (W - 2r) = 0
Solving for W: 8r + 44π + 60 - W = W - 2r
Simplifying: 10r + 44π + 60 = 2W
W = 5r + 22π + 30
Now that we have W in terms of r, we can substitute this expression back into the area equation to get the area in terms of r only.
A = (4r + 22π + 30 - (5r + 22π + 30)) ((5r + 22π + 30) - 2r)
Simplifying: A = (r - 22π) (3r + 22π + 30)
Expanding: A = 3r² + 8rπ + 30r - 66πr - 660π
Now, to find the maximum area, we can take the derivative of A with respect to r, set it equal to zero, and solve for r.
dA/dr = 6r + 8π + 30 - 66π = 0
Simplifying: 6r - 58π + 30 = 0
6r = 58π - 30
r = (58π - 30) / 6
r ≈ 29π/3 - 5
Therefore, to maximize the seating area while using 45π + 60 meters of light strips, the radius of the semicircular stage should be approximately 29π/3 - 5 meters.
Learn more about maximum area click;
https://brainly.com/question/29635164
#SPJ12
out of 80 people surveyed, 4 said they don't like eating ice cream. would it be appropriate to run a proportion test, with approximating with the normal distribution, to see if less than 10% of people don't enjoy eating ice cream? group of answer choices since we do not know the standard deviation, the test is not appropriate. since the observed number of successes and failues (4, 76) are not both greater than 5, the test is not appropriate. since our sample size is 80, which is greater than 30, the central limit theorem applies, and the test is appropriate. since the hypothesized number of successes and failues (8, 72) are both greater than 5, the test is appropriate. since our data represents a portion out of a whole, the test is appropriate
Answers
Based on the information provided, it would be appropriate to run a proportion test to see if less than 10% of people don't enjoy eating ice cream. The appropriate answer choice would be: since our sample size is 80, which is greater than 30, the central limit theorem applies, and the test is appropriate. The correct answer is C).
The central limit theorem states that as the sample size increases, the distribution of the sample means becomes more normal, regardless of the distribution of the original population.
In this case, with a sample size of 80, the central limit theorem applies, and we can approximate the sampling distribution of the proportion of people who do not enjoy eating ice cream with a normal distribution. So, the correct option is C).
To know more about central limit theorem:
https://brainly.com/question/18403552
#SPJ4
Can someone help me with number 36? Tysmmm

Answers
Answer: Never(!) [assuming I understand/interpret the question properly]
Step-by-step explanation: The question wants to know how many months it will take for your neighbor's total cost be the same as yours, with three televisions. One has to interpret "total cost." I deem it to be the total accumulated costs, including installation. If you interpret it as the cost per month, then they charges are the same after the month the installation cast was paid. That's because the satellite provider charges per television, and 3*(13.32) is equal to the same 39.96/month charged by the cable provider. It the questions means total cumulative costs, the satellite customer will never exceed the cable customer's total bill, because of the installation fee ($75 for cable and free for satellite)
The equation of a line is x+3y=14
Answers
Answer:
then slope intercept form would be
y= -1/3 x +14/3
the slope would be -1/3
the y-intercept would be 14/3
Step-by-step explanation:
plz brainliest :)
which triangle is the most similar to triangle ABC?

Answers
Answer J is the answer, it is the only answer that has a ratio between the given shape of 1:2, the dilation is 1/2 or x2 if you're going from object J to ABC.
what does it mean when the second derivative equals zero
Answers
When the second derivative of a function equals zero, it indicates a possible point of inflection or a critical point where the concavity of the function changes. It is a significant point in the analysis of the function's behavior.
The second derivative of a function measures the rate at which the slope of the function is changing. When the second derivative equals zero at a particular point, it suggests that the function's curvature may change at that point. This means that the function may transition from being concave upward to concave downward, or vice versa.
Mathematically, if the second derivative is zero at a specific point, it is an indication that the function has a possible point of inflection or a critical point. At this point, the function may exhibit a change in concavity or the slope of the tangent line.
Studying the second derivative helps in understanding the overall shape and behavior of a function. It provides insights into the concavity, inflection points, and critical points, which are crucial in calculus and optimization problems.
learn more about derivatives :
https://brainly.com/question/25324584
#SPJ4
When the second derivative of a function equals zero, it indicates a critical point in the function, which can be a maximum, minimum, or an inflection point.
The second derivative of a function measures the rate at which the slope of the function is changing. When the second derivative equals zero, it indicates a critical point in the function. A critical point is a point where the function may have a maximum, minimum, or an inflection point.
To determine the nature of the critical point, further analysis is required. One method is to use the first derivative test. The first derivative test involves examining the sign of the first derivative on either side of the critical point. If the first derivative changes from positive to negative, the critical point is a local maximum. If the first derivative changes from negative to positive, the critical point is a local minimum.
Another method is to use the second derivative test. The second derivative test involves evaluating the sign of the second derivative at the critical point. If the second derivative is positive, the critical point is a local minimum. If the second derivative is negative, the critical point is a local maximum. If the second derivative is zero or undefined, the test is inconclusive.
Learn more:About second derivative here:
https://brainly.com/question/29090070
#SPJ11
The temperature was 70 degrees. At noon, the temperature increased by 8 degrees. By evening, the temperature decreased by 8 degrees. What is the final temperature?
Answers
Answer:
The answer is 70 you would add the 8 degrees but them subtract it again
What is the answer to 7x^3-1 by x+2
Answers
Answer:
7x over3 -b x y +2
Step-by-step explanation:
5. a rectangular carpet is 3m wide and 7m long. find the area of the carpet in square metres.
Answers
Answer:
21m²
Step-by-step explanation:
area = length X width
= 7 X 3
= 21m²
The dot plots show the heights of boys and girls at a summer camp. Heights of Boys and Girls at Camp 2 dot plots with number lines going from 40 to 60. A plot is titled Boy's Heights. There are 0 dots above 40, 1 above 41, 3 above 44, 3 above 46, 2 above 48, 3 above 50, 4 above 52, 4 above 54, and 0 above 56, 58, and 60. A plot is titled Girl's Heights. There are 0 dots above 40 and 41, 2 dots above 44, 3 above 46, 1 above 48, 3 above 50, 4 above 52, 3 above 54, 4 above 56, and 0 above 58 and 60. Which is a true statement for most of the data in each plot? Most of the data in each plot are greater than 48. Most of the data in each plot are less than 48. Most of the data in each plot are around 52. Most of the data in each plot are around 54. Mark this and return
Answers
Most of the data in each plot are greater than 48.
How to determine the correct option?1. Boy's Heights.
Using the information you can create a frequency table:
Height Frequency
40 0
41 1
44 3
46 3
48 2
50 3
52 4
54 4
56 0
58 0
60 0
======
20 boys
2. Girl's Heights.
Similarly, create your frequency table:
Height Frequency
40 0
41 0
42 0
44 2
46 3
48 1
50 3
52 4
54 3
56 4
58 0
60 0
======
20 girls
Most of the data in each plot are greater than 48.
Count the dots or add the frequencies from the tables.
For boys, the frequency of points greater than 48 is: 3 + 4 + 4 = 11 which is more than half (there are 20 dots).
For girls, the frequency of points greater than 48 is: 3 + 4 + 3 + 4 = 14, which is also more than half.
Hence, it is correct that most of the data in each plot are greater than 48.
Learn more about frequency table on https://brainly.com/question/28931302
#SPJ1
What is the smallest power of 10 that would exceed 999,999,999,991
Answers
Answer:
Answer is 10^11 is the smallest power that would exceed 999,999,999,991
Answer:
10 to the power of 13 or 10^13
Find the slope.
−1/2
1/2
−7/6
−2

Answers
Answer:
(-1 2) (7 6) is the answer to the question
Answer:
-1/2
Step-by-step explanation:
slope= -7-(-5)/6-2
= -7+5/4
= -2/4
= -1/2
Given = -10] -3 -6 2 -0-0 and 16 find the closest point to in the subspace W spanned by
Answers
Therefore, the closest point in the subspace W to the given point is approximately 1.874, 6.006, 7.367, 5.599.
To find the closest point in the subspace W spanned by the vectors -6, 4, -4, 1 and 2, 5, 6, 16 to the given point given = -10 ,-3 ,-6 ,2 ,-0,-0 and 16, we can use the projection formula.
Let's call the given point "P" and the vectors spanning the subspace "v₁" and "v₂."
Calculate the projection of point P onto vector v₁:
proj(v₁) = ((P · v₁) / v₁²) × v1
Calculate the projection of point P onto vector v₂:
proj(v₂) = ((P · v₂) / v₂²) × v₂
Find the closest point Q in the subspace W to point P:
Q = proj(v₁) + proj(v₂)
Let's calculate it step by step:
Step 1:
Given point P:-10, -3, -6, 2, -0, -0, 16
Vector v₁: -6, 4, -4, 1
Vector v₂: 2, 5, 6, 16
Dot product of P and v₁:
P · v₁ = ((-10) × (-6)) + ((-3) × 4) + ((-6) ×( -4)) + (2 ×1) + (0 × 0) + (0 × 0) + (16 × 1) = 60
Magnitude (norm) of v₁:
v₁ = √((-6)² + 4² + (-4)² + 1²) =√(36 + 16 + 16 + 1) = √(69)
Projection of P onto v₁:
proj(v₁) = (P · v₁/v₁²) v₁
= (60 / 69) × (-6), 4, -4, 1
=((-60)/69) × 6, (60/69) ×4, ((-60)/69) × (-4), (60/69) × 1
= (-40)/23, 80/23, 80/23, 60/69
Step 2:
Dot product of P and v₂:
P · v₂ = ((-10) × 2) + ((-3) ×5) + ((-6) × 6) + (2 ×16) + (0× 0) + (0 × 0) + (16 × 16) = 248
Magnitude (norm) of v₂:
v₂ = √(2² + 5² + 6² + 16²) =√(4 + 25 + 36 + 256) = √(321)
Projection of P onto v₂:
proj(v₂) = (P · v₂ / v₂²) × v₂
= (248 / 321)× 2, 5, 6, 16
=(248/321) × 2, (248/321) × 5, (248/321) × 6, (248/321) × 16
= 496/321, 1240/321, 1488/321, 3968/321
Step 3:
Closest point Q in the subspace W to point P:
Q = proj(v₁) + proj(v₂)
= (-40)/23, 80/23, 80/23, 60/69]+ 496/321, 1240/321, 1488/321, 3968/321
= ((-40)/23) + (496/321), (80/23) + (1240/321), (80/23) + (1488/321), (60/69) + (3968/321)
= 1356/723, 4344/723, 5328/723, 4048/723
Therefore, the closest point in the subspace W to the given point is approximately 1.874, 6.006, 7.367, 5.599.
To know more about subspace:
https://brainly.com/question/32256518
#SPJ4
At the ice cream shop, there are 28 flavors of ice cream available. How many ways can you select a bowl of 5
scoops of ice cream if each scoop is a different flavor?
Answers
There are 98,280 ways to select a bowl of 5 scoops of ice cream from 28 available flavors if each scoop is a different flavor.
To solve this problem, we can use the formula for combinations, which is nCr = n! / r! (n-r)!, where n is the total number of items, r is the number of items we want to select, and ! means factorial (multiply all numbers from 1 to n together).
In this case, we have 28 flavors of ice cream and we want to select 5 scoops.
So we can plug in n = 28 and r = 5:
28C5 = 28! / 5!(28-5)!
= 28! / 5!23!
= (28x27x26x25x24) / (5x4x3x2x1)
= 98,280
Therefore, there are 98,280 ways to select a bowl of 5 scoops of ice cream from 28 available flavors if each scoop is a different flavor.
Summary: There are 98,280 ways to select 5 scoops of ice cream from 28 flavors if each scoop is a different flavor, using the formula for combinations.
learn more about combinations click here:
https://brainly.com/question/28065038
#SPJ11
A point (8, c) lies on the line y = 3x + 2. Work out the value of c.
Answers
y=3*8+2=26
Therefor the answer for c is 26
[please help] A data set lists the grade point averages of 9th grade students. Which of the following charts could be used to display the data, and why? A) Box plot; because the data is categorical B) Box plot; because the data is numerical C) Circle graph; because the data is categorical Circle graph D)because the data is numerical
Answers
Answer: B) Box plot; because the data is numerical.
Step-by-step explanation:
first off this question contains numerical data only, so we can eliminate A & C because they are talking about categorical data. D states "circle graph; because the data in numerical", which circle graphs are in fact not numerical, but categorical data. So since D is incorrect the only one left is B that says box plots because the data is numerical, which is correct. therefore the answer is D. :)
Answer:
B- Box plot because the data is numerical
Step-by-step explanation:
i took the test :)
Which property justifies "Step 4"
Which property justifies "Step 4" in the proof below?
a. )45= m_B
b.) m B = 45
3) Substitution
4)?
Answers
The property justified by step 4 is after substitution in the equation you get the desired result.
What is an expression?Mathematical actions are called expressions if they have at least two terms that are related by an operator and include either numbers, variables, or both. Adding, subtraction, multiplying, and division are all reflection coefficient operations. A mathematical operation such as reduction, addition, multiplication, or division is used to integrate terms into an expression.
As per the data in the question,
In step 3 substitution of value is taking place.
In step 4 when values are substituted the final result is obtained, so step 4 is the result step.
To know more about an expression:
https://brainly.com/question/14083225
#SPJ1
How many solutions does the equation 4x 8 = −2 − 2 5x have? two one none infinitely many
Answers
The equation 4x+8 = -2-2+5x has only one solution x=12.
Given equation is:
4x+8 = -2-2+5x
What is an equation?An equation is an operator (denoted by =) that equates the two expressions.
On bringing variables to the left side and constants on the right side
4x-5x = -2-2-8
-x = -12
x =12
Therefore, the equation 4x+8 = -2-2+5x has only one solution x=12.
To get more about equations visit:
https://brainly.com/question/2972832
A jacket at a clothing store is being discounted by 10%. If the jacket was originally priced at x dollars, which of the following expressions does NOT represent the final price of the jacket before sales tax is added?
A.0.90x
B.x – 0.10x
C.x – 1.10x
D.x(1 – 0.10)
Answers
Answer:a
Step-by-step explanation:
Answer: I'm pretty sure its answer D
