Answers
Answer: 60 degrees
Step-by-step explanation: triangles are come to 180 if you add all angles correctly. therefore if you do 180-90-30, you'll get 60.
Related Questions
To divide
by
, answer this question: How many sets of
are in
? Use the model representing the fraction
to help you answer the question. (Hint: Think about grouping the blue boxes into pairs.)
Answers
Help me out and show me the full solution on how you solved it, please!

Answers
The value of each trigonometric identity is:
3/2
5/6
14/3
We have,
We will use the trigonometric formula and substitute the given values.
So,
Cosec θ
This can be written as,
= 1/ sin θ
= 1/(2/3)
= 3/2
And,
Sin θ
This can be written as,
= 1/ cosec θ
= 1/(6/5)
= 5/6
And,
Sec θ
This can be written as,
= 1/cosθ
= 1/(3/14)
= 14/3
Thus,
The value of each trigonometric identity is:
3/2
5/6
14/3
Learn more about trigonometric identities here:
https://brainly.com/question/14746686
#SPJ1
Katrina bought new shoes for $55.00, jeans for $29.99, and a new blouse for $27.79. Sales tax in her area is 7 percent. What was the total charge for her purchases?
Answers
Answer:
$120.67
Step-by-step explanation:
1. 55+29.99+27.79 = 112.78
2. 7% of 112.78 is 7.89
:)
Math question :D
Need help

Answers
Answer:
77
Step-by-step explanation:
c + 103 = 180
180- 103 = 77
c and b = 77
hey can you guys help me please? i kinda need it....
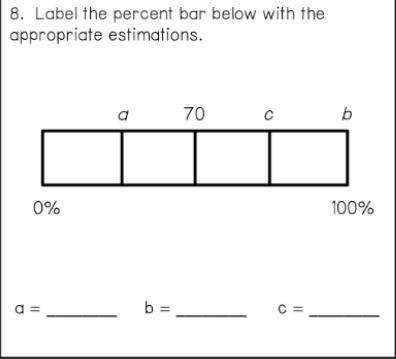
Answers
Answer:
Hey! Ok so the answers are A.50% B.100% C.80%
Step-by-step explanation:
Just predict the number to what they're next to.
Hoped this helped Im Eve btw. Hope you have a great day and consider marking this brainliest Thank you so much if you do! ✨
1. Find the coordinates of the midpoint of AB for A(5, 12) and B(-4, 8).
2. Find the coordinates of G if P (-5,10) is the midpoint of EG and E has coordinates (-8,6).
Answers
1) The midpoint of AB for A(5, 12) and B(-4, 8) is (1/2, 10)
2) The coordinate of G will be at (-2, -20) if P (-5,10) is the midpoint of EG and E has coordinates (-8,6).
The midpoint of a line is the point that divides such a line into two equal parts.
The formula for calculating the midpoint of a line is expressed as:
\(M(X, Y) =(\frac{x_1+x_2}{2} ,\frac{y_1+y_2}{2} )\)
1) Given the coordinates A(5, 12) and B(-4, 8).
X = (5+(-4))/2
X = (5-4)/2
X = 1/2
Get the coordinate Y
Y = (12+8)/2
Y = 20/2
Y = 10
Hence the coordinate of the midpoint of AB for A(5, 12) and B(-4, 8) is
(1/2, 10)
The formula for calculating the midpoint of a line is expressed as:
\(M(X, Y) =(\frac{x_1+x_2}{2} ,\frac{y_1+y_2}{2} )\)
1) Given the midpoint P (-5, 10) and the coordinate (-8, 6)
Get the X coordinate of G
X = (x1+x2)/2
-5 = (x1-8)/2
-10 = x1 - 8
x1 = -10 + 8
x1 = -2
Get the Y coordinate of G
Y = (y1+y2)/2
10 = (y1+8)/2
20 = y1+8
y1 = 20-8
y1 = 12
Hence the coordinate of G will be at (-2, -20)
Learn more here; https://brainly.com/question/3510899
please help! I don’t really have a grasp on word problems and they tend to stress me out a lot.

Answers
Answer:
Imani: 13r + 3d = 63
Abhasra: 12r + 12d = 132
Step-by-step explanation:
You just fill in the answers from the word problem. It has the answers.
Calculate the mean number of orange M&M's in a small bag.

Answers
Answer:
5.5
Step-by-step explanation:
mean is the synonym for average
to calculate the mean/average , u add all the numbers(the total amount) and then divide it by how many numbers there is.
3+4+5+6+7+8=33
33÷5=5.5
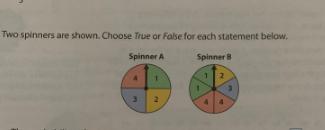
the probability of spinning a1 is the same for both spinners ture or false
Answers
The probability of spinning a 1 is the same for both spinners: False
How to determine the true statement?The spinners that complete the question are added as an attachment
From the attached figures, we have
Spinner 1
Number of 1 = 1
Sections = 4
Spinner 2
Number of 1 = 2
Sections = 6
The probability of obtaining 1 is calculated as
P(1) = Number of 1/Sections
So, we have
Spinner 1
Number of 1 = 1
Sections = 4
P(1) = 1/4
Spinner 2
Number of 1 = 2
Sections = 6
P(1) = 2/6
By comparison
1/4 and 2/6 do not have the same value
Hence. it is false that the probability of spinning a 1 is the same for both spinners
Read more about probability at
https://brainly.com/question/251701
#SPJ1
Given \tan A=\frac{11}{60}tanA=
60
11
and that angle AA is in Quadrant I, find the exact value of \cos AcosA in simplest radical form using a rational denominator.
Answers
Answer: 60/61
Step-by-step explanation:

A cell phone company charges $42 per month of service. The cost of a new
cell phone, plus 8 months of service, is $415.99. How much does it cost to
buy a new cell phone and 3 months of service?
Answers
Answer:
$1247.97
Step-by-step explanation:
$42 per month of service
new phone monthly service is $415.99
415.99 x 3 = 1247.97
Help me with this :)))))))

Answers
Answer:
QR= 16
Step-by-step explanation:
HOPE THIS HELPS

(x^2 times x^3)^3
Some body please help me
Answers
\( = (x^2 \times x^3)^3 \\ = x {}^{6} \times {x}^{9} \\ = (x) {}^{6 + 9} \\ = {x}^{15} \)
When the bases are the same and they are multiplying we take one base, consider the exponents and add them
=(x^(2+3))^3
=(x^5)^3
=x^(5 X 3)
=x^15
The sum of the speeds of two trains is 717.4 miles per hour. If the speed of the first train is 4.6 miles per hour faster than that of the second train, find the speed of each
Answers
Answer:
The second train speed is 356.4 miles per hour
And, the first train speed is 361 miles per hour
Step-by-step explanation:
The computation of the speed of each train is as follows
Given that
The Sum of the speed of two trains is 717.4 miles per hour
Let us suppose the second train speed be x
So for the first train, the speed is x + 4.6
Now the equation is
x + x + 4.6 = 717.4
2x + 4.6 = 717.4
2x = 717.4 - 4.6
2x = 712.8
x= 356.4
Therefore the second train speed is 356.4 miles per hour
And, the first train speed is = 356.4 + 4.6 = 361 miles per hour
HELP MEEEEEEEEEEEEEEEEEEEEEEEE PLEASEEEEEEEEEEEEEEEEEEEEE!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer: 636,000
Step-by-step explanation:
1. 8% of 300,000 is 24,000
2. Multiply 24,000 by 14 to get 336,000
3. Add 300,000 to 336,000
If this is incorrect, I think I know what I could have done wrong so just lmk
5 [³F(x) Find # f(x) dx if f(x) = = {3 if x < 3 x if x ≥ 3.
Answers
The value of the definite integral ∫[5 to ³] f(x) dx, if f(x) = = {3 if x < 3 x if x ≥ 3, is 2.
To find the definite integral of the function f(x), we need to split the integral into two parts since the function has a different definition for x less than 3 and x greater than or equal to 3. Let's calculate the integral step by step:
For x < 3:
∫[a to b] f(x) dx = ∫[a to b] 3 dx
Since the function is constant, the integral becomes:
∫[a to b] 3 dx = 3x + C
For x ≥ 3:
∫[c to d] f(x) dx = ∫[c to d] x dx
Integrating x with respect to x, we get:
∫[c to d] x dx = (1/2)x^2 + C
Now, to find the definite integral of f(x) from 5 to ³, we need to evaluate both parts of the integral separately and subtract the result for the lower limit from the result for the upper limit.
∫[5 to ³] f(x) dx = [∫[5 to ³] 3 dx] - [∫[5 to ³] x dx]
Evaluating the integrals individually:
[∫[5 to ³] 3 dx] = 3x | [5 to ³] = 3(³) - 3(5) = 9 - 15 = -6
[∫[5 to ³] x dx] = (1/2)x^2 | [5 to ³] = (1/2)(³)^2 - (1/2)(5)^2 = (1/2)(9) - (1/2)(25) = 4.5 - 12.5 = -8
Finally, we subtract the result for the lower limit from the result for the upper limit:
∫[5 to ³] f(x) dx = -6 - (-8) = -6 + 8 = 2
Therefore, the value of the definite integral ∫[5 to ³] f(x) dx is 2.
To know more about integrals, visit the link : https://brainly.com/question/30094386
#SPJ11
(2X-7)°
(3X+5)°
153°

Answers
Answer:
x = 31°
Step-by-step explanation:
The rightmost corner of the triangle is where we start.
We know that a line has 180° in it, therefore to find that angle, simply do:
180° - 153° = 27°
We also know that there are 180° in a triangle, write an equation for the triangle:
(2x-7)° + (3x+5)° + 27° = 180°
Combine like terms:
5x° + 25° = 180°
Subtract 25° from both sides:
5x° = 155°
Divide both sides by 5°:
x = 31°
Multiply the binomials: (8a - 3b) (3a - 8b)
Answers
Answer:
24a²-73ab+24b²
Step-by-step explanation:
(8a - 3b) (3a - 8b) =
24a²-64ab-9ab+24b²
= 24a²-73ab+24b²
Why a sample is always smaller than a population?
Answers
Answer:
A sample is a subset of the population.
Can someone help me do these problems?

Answers
The solutions using laws of exponents are:
a) \((4x)^{\frac{3}{2} }\)= \(8 \sqrt[]{x^{3} }\)
b) \(x^{\frac{-2}{3}}\)\(= \sqrt[3]{x^{2} }\)
d) \(\frac{\sqrt[3]{x} }{\sqrt{x} }\)\(=\) \(\sqrt[3]{x^{2} }\)
e) \(\frac{\sqrt{x} * x^{2} }{{x^{\frac{5}{2} } } }\)= 1
How to use laws of exponents?Some of the laws of exponents are:
- When multiplying by like bases, keep the same bases and add exponents.
- When raising a base to a power of another, keep the same base and multiply by the exponent.
- If dividing by equal bases, keep the same base and subtract the denominator exponent from the numerator exponent.
The expression we want to solve is given as:
a) \((4x)^{\frac{3}{2} }\)
Using laws of exponents, the bracket is simplified to get:
\(4^{\frac{3}{2}} * x^{\frac{3}{2}}\)
= \(8 \sqrt[]{x^{3} }\)
b) The expression we want to solve is given as:
\(x^{\frac{-2}{3}}\)
This simplifies to get:
\(\sqrt[3]{x^{2} }\)
d) The expression we want to solve is given as:
\(\frac{\sqrt[3]{x} }{\sqrt{x} }\)
This simplifies to get:
\(x^{\frac{-2}{3}}\) = \(\sqrt[3]{x^{2} }\)
e) The expression we want to solve is given as:
\(\frac{\sqrt{x} * x^{2} }{{x^{\frac{5}{2} } } }\)
This simplifies to get:
\(\frac{{x^{\frac{5}{2} } } }{{x^{\frac{5}{2} } } }\)
= 1
Read more about Laws of Exponents at: brainly.com/question/11761858
#SPJ1
. A jar on your desk contains fourteen black, nine red, eleven yellow, and three green jellybeans. You pick a jellybean without looking. Find the odds of picking a black jellybean.
Answers
The odds of picking a black jellybean are 14 to 23. This means that for every 14 black jellybeans, there are 23 non-black jellybeans in the jar.
To find the odds of picking a black jellybean, we need to determine the probability of picking a black jellybean and the probability of not picking a black jellybean.
The total number of jellybeans in the jar is 14 + 9 + 11 + 3 = 37.
The probability of picking a black jellybean is the number of black jellybeans divided by the total number of jellybeans:
P(black) = \(\frac{14}{37}\)
The probability of not picking a black jellybean is the complement of picking a black jellybean, which is 1 minus the probability of picking a black jellybean:
P(not black) = 1 - P(black) = \(\begin{equation}1 - \frac{14}{37} = \frac{23}{37}\)
The odds of picking a black jellybean are given by the ratio of the probability of picking a black jellybean to the probability of not picking a black jellybean:
\(\text{Odds}(black) = \frac{P(black)}{P(\text{not black})} = \frac{\frac{14}{37}}{\frac{23}{37}} = \frac{14}{23}\)
Therefore, the odds of picking a black jellybean are 14 to 23.
To know more about the probability refer here,
https://brainly.com/question/32117953#
#SPJ11
Suppose that P = (x, y) has polar coordinates (r, π/7). Find the polar coordinates for the following points if 0 € [0,2π]. (a) P = (x, -y) (Give your answer in the form (*,*). Express numbers in exact form. Use symbolic notation and fractions where needed.) polar coordinates:
Answers
If the point P has polar coordinates (r, π/7), then we have:
x = r cos(π/7) and y = r sin(π/7)
(a) To find the polar coordinates of P' = (x, -y), we need to first determine its Cartesian coordinates:
x' = x = r cos(π/7)
y' = -y = -r sin(π/7)
The distance from the origin to P' is:
r' = sqrt(x'^2 + y'^2) = sqrt((r cos(π/7))^2 + (-r sin(π/7))^2) = sqrt(r^2 (cos(π/7))^2 + r^2 (sin(π/7))^2)
= sqrt(r^2 (cos(π/7))^2 + r^2 (sin(π/7))^2) = sqrt(r^2 (cos^2(π/7) + sin^2(π/7))) = sqrt(r^2) = r
The angle that P' makes with the positive x-axis is:
θ' = atan2(y', x') = atan2(-r sin(π/7), r cos(π/7)) = atan2(-sin(π/7), cos(π/7))
We can simplify this expression using the formula for the tangent of a difference of angles:
tan(π/7 - π/2) = -cot(π/7) = -1/tan(π/7) = -sin(π/7)/cos(π/7)
Therefore, the polar coordinates of P' are (r, θ') = (r, π/2 - π/7) = (r, 5π/14).
Hence, the polar coordinates of P' are (r, θ') = (r, 5π/14).
To know more about polar coordinates , refer here :
https://brainly.com/question/1269731#
#SPJ11
The perimeter of a rectangular garden is 48.8 feet it’s length is 12.4 what is it’s width
Answers
Answer:
12 feet
Step-by-step explanation:
Perimeter=l+l+w+w
48.8=12.4+12.4+2w
48.8=24.8+2w
2w=24, w=12 feet
Yemi is 5 years older than kunle.The product of their ages is 750. How old is kunle.
Answers
Answer:
Kunie is 25
Step-by-step explanation:
Let's make Yemi's age y, and Kunie's age k.
Because Yemi is 5 years older that Kunie, k + 5 = y.
Because the product of their ages is 750, k * y = 750.
With substitution, we can determine that k * (k + 5) = 750.
Then with distributive property we can simplify the equation to get k^2 + 5k = 750.
Then we bring all the terms to one side of the equation to get k^2 + 5k - 750 = 0.
Then with quadratics, we can factor the equation to get (k + 30)(k - 25)=0.
Thus, either k + 30 must equal 0, or k - 25 must equal 0. Thus, k must equal 25 or -30, and because someone cannot be -30 years old, k = 25.
Then, because Yemi is 5 years older than Kunie, y = 30.
Hope it helps <3
Kunle's age is marked as k.
Yemi's age is therefore k + 5.
The product of k and k + 5 equals 750.
What is k?
Now that we have tought this through...
Here is the equality:
\(k(k+5)=750\)
Expanding the parentheses and subtracting 750 from both sides gives you
\(k^2+5k-750=0\)
Which is a second degree polynomial (ie. quadratic equation).
That means there are two solutions of what Kunle's age might be.
\(k^2+5k-750=0\)
\(k^2+30k-25k-750=0\)
\(k(k+30)-25(k+30)=0\)
\((k+30) (k-25) =0\implies k_1=-30, k_2=25
\)
So we got two results and since age cannot be negative that leaves us with one result and that is 25.
TL;DR The answer is: Kunle is 25 years old.
Hope this helps.
Do you have an equal chance of landing on either 1 or 3?

Answers
Answer:
Yes
Step-by-step explanation:
There are 3 triangles for both 1 and 3 and 12 triangles in total.
The chance of getting 1 is 3/12 and the chance of getting 3 is 3/12
Since 3/12 = 3/12 then the chances are equal.
Answer:
3 because it's a most common number 1 Is rare
2. 8 × - 11 - 3× + 8
please solve this thankyou!!
Answers
Answer:
-54.8 ( in fraction -274/5)Step-by-step explanation:
2.8 × (-11) - 3 × 8 =
-30.8 - 24 =
-54.8 ( in fraction -274/5)
Barrett works at an ice cream shop. the function f(x) represents the amount of money in dollars barrett earns per gallon of ice cream, where x is the number of gallons of ice cream he makes. the function g(x) represents the number of gallons of ice cream barrett makes per hour, where x is the number of hours he works. f(x) = 2x2 4 g(x) = the square root of three times x cubed find f(g(x)). f of g of x equals the square root of the quantity 6 times x to the fifth power plus 4 dollars over hour f of g of x equals the square root of the quantity 6 times x to the fifth power plus 4 gallons over hour f(g(x)) = 6x3 4 gallons over hour f(g(x)) = 6x3 4 dollars over hour
Answers
Amount of money earned per number of hours of work = \(f(g(x)) = 6x^{3} + 4\)
What is a composite function?A composite function is generally a function that is written inside another function. Composition of a function is done by substituting one function into another function. For example, f [g (x)] is the composite function of f (x) and g (x). The composite function f [g (x)] is read as “f of g of x”.To evaluate a composite function f(g(x)) at some x = a, first compute g(a) by substituting x = a in the function g(x). Then substitute g(a) into the function f(x) by substituting x = g(a). In the same way, we can calculate g(f(a)) as well.
Required calculation -
Amount of money (the earning) per unit x = \(f(x) = 2x^{2} + 4\)
Number of gallons of ice cream that Barrett makes per hour, where x is the number of hours he works = \(g(x) = \sqrt{3x^{3}}\)
we are to find the composite function \(f(g(x))\)
Substituting g(x) into the x of f(x), we find:
\(f(g(x)) = 2(\sqrt{3x^{3} } )^{2} + 4\\\\= 2(3x^{3} ) + 4\\= 6 x^{3} + 4\)
To learn more about composite function from given link
https://brainly.com/question/14865610
#SPJ4
Answer:
f(g(x)) = 6x3 + 4 dollars over hour
Step-by-step explanation:
someone please help??

Answers
How many hours pass between the two temperatures shown?

Answers
Answer:
7 . time os on axis X. total vector lenght is 7.
Simplify to create an equivalent expression. 8(10-6q)+3(-7q-2)}8(10−6q)+3(−7q−2)
Answers
Step-by-step-explanation:
Answer:
-69q+74
Step-by-step explanation:
Distribute:
80-48q-21q-6
Simplify:
74-69q
