Answers
\(\huge\boxed{(-2)^2x^3y^2}\)
___________________________________________________________
\(\boxed{Explanation}\)
\((-2)\;*(-2)=(-2)^2\\x*x*x=x^3\\y*y=y^2\\\\Add\;them\;all\;together\;and\;you\;get\;(-2)^2x^3y^2.\)
Hope it helps!
May i have brainliest?
\(\huge\boxed{Thanks,\;Plip.}\)
Related Questions
help please !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!111

Answers
Jenna and Mia arrived at the same answer because both the methods they have adopted are correct.
Given solution of a question done by two people.
Jenna's method
5(30+4)
(5)(30)+(5)(4)
150+20=170
Mia's method
5(30+4)
5(34)=170
We are required to find why they have achieved at the same answer.
Jenna and Mia have achieved at the same answer because they both have adopted the right method.Jenna's method is the equation in its simplest form. Addition of that is easily understood. While Mia's method is just valid as Jenna's some people may have trouble remembering the steps of multiplication within parantheses as well as being able to look at large multiplication problem and automatically knowing the answer or being able to get the answer as fast as simple addition.
Hence Jenna and Mia arrived at the same answer because both the methods they have adopted are correct.
Learn more about multiplication at https://brainly.com/question/10873737
#SPJ1
I NEED SERIUOS HELPPP

Answers
The regression line equation, can be found to be y = 0.90x - 3.79
How to find the regression equation ?Find the slope using the slope formula :
m = ( 5 x 1944 - 98 x 69 ) / ( 5 x 2580 - 98² )
m = ( 9720 - 6762 ) / ( 12900 - 9604 )
m = 2958 / 3296
= 0.8975
Then find the y - intercept :
b = ( 69 - 0. 8975 x 98) / 5
b = ( 69 - 87. 945) / 5
b = - 18. 945 / 5
= - 3.789
The regression equation is:
y = 0.90x - 3.79
Find out more on regression equation at https://brainly.com/question/27997774
#SPJ1
which expression is equivalent to 3(x-2)+2x
A. -x
B. 3x
C. 5x-2
D. 5x-6
Answers
Anna paints landscapes and still-lifes. She buys canvases and paint for a cost of $3 per painting, and paints either a landscape or a still-life on each canvas. If she sells l landscapes for $20 each, and s still-lifes for $15 each, which of the following expressions represents Anna’s profit, P, in dollars?
Answers
The profit made by Anna in terms of l and s is, P= 17 l + 12 s.
What is Algebra?A branch of mathematics known as algebra deals with symbols and the mathematical operations performed on them.
Variables are the name given to these symbols because they lack set values.
In order to determine the values, these symbols are also subjected to various addition, subtraction, multiplication, and division arithmetic operations.
Given:
Anna buys canvases and paint for a cost of $3 per painting.
If she sells 'l' landscapes for $20 each,
and 's' still - life for $15 each.
So, The Profit can find as
P = 20 l + 15s - 3(s+ l)
P = 20l + 15s - 3s- 3l
P = 17 l + 12 s
Hence, the expressions represents Anna’s profit is P = 17 l + 12 s.
Learn more about Algebra here:
https://brainly.com/question/24875240
#SPJ1
G(Q) = 5 + 3Q + 202 - Q2 C2(Q) = 3 + 4Q + 2 1. Find the MC function for both C1(Q) AND C2(Q). 2. Find AVC function for both Ci(Q) AND C2(Q). 3. Find AFC function for both C1(Q) AND C2(Q). 4. Find AC function for both Ci(Q) AND C2(Q). 5. Find ATC function for both Ci(Q) AND C2(Q).
Answers
For C1(Q) = 3 - 2Q.
For C2(Q) = 4.
2. The AVC function
For C1(Q) = 5/Q + 3 + 20/Q - Q.
For C2(Q) = 3/Q + 4 + 2/Q.
3. The AFC function
For C1(Q)= 5/Q - 20/(5 + 3Q + 20/Q - Q)
For C2(Q) = 0.
4. To find the AC function
For C1(Q) = (5 + 3Q + 202 - Q^2)/Q + 5/Q - 20/(5 + 3Q + 20/Q - Q).
For C2(Q) = (3 + 4Q + 2)/Q + 3/Q + 4 + 2/Q.
5.To find the ATC function
For C1(Q)= 5/Q² + 3/Q + 20/Q² - Q/Q + 5/Q - 20/(5Q + 3Q² + 20 - Q²)
For C2(Q)= 3/Q² + 4/Q + 2/Q² + 3/Q + 4/Q + 2/Q.
Find the ATC functions for C1(Q) and C2(Q) given the provided cost functions?
1. To find the MC function, we take the derivative of the cost functions with respect to Q.
For C1(Q) = 5 + 3Q + 202 - Q^2, MC1(Q) = 3 - 2Q.
For C2(Q) = 3 + 4Q + 2, MC2(Q) = 4.
2. To find the AVC function, we divide the cost functions by Q.
For C1(Q), AVC1(Q) = (5 + 3Q + 202 - Q^2)/Q = 5/Q + 3 + 20/Q - Q.
For C2(Q), AVC2(Q) = (3 + 4Q + 2)/Q = 3/Q + 4 + 2/Q.
3. To find the AFC function, we subtract the AVC function from the ATC function.
For C1(Q), AFC1(Q) = (5 + 3Q + 202 - Q^2)/Q - (5 + 3Q + 202 - Q^2)/(5 + 3Q + 20/Q - Q)
= 5/Q - 20/(5 + 3Q + 20/Q - Q).
For
C2(Q), AFC2(Q) = (3 + 4Q + 2)/Q - (3 + 4Q + 2)/(3/Q + 4 + 2/Q) = 0.
4. To find the AC function, we add the AVC function to the AFC function.
For
C1(Q), AC1(Q) = (5 + 3Q + 202 - Q^2)/Q + 5/Q - 20/(5 + 3Q + 20/Q - Q).
For
C2(Q), AC2(Q) = (3 + 4Q + 2)/Q + 3/Q + 4 + 2/Q.
5. To find the ATC function, we divide the AC function by Q.
For
C1(Q), ATC1(Q) = [(5 + 3Q + 202 - Q²)/Q + 5/Q - 20/(5 + 3Q + 20/Q - Q)]/Q
= 5/Q² + 3/Q + 20/Q² - Q/Q + 5/Q - 20/(5Q + 3Q² + 20 - Q²).
For
C2(Q), ATC2(Q) = [(3 + 4Q + 2)/Q + 3/Q + 4 + 2/Q]/Q
= 3/Q² + 4/Q + 2/Q² + 3/Q + 4/Q + 2/Q.
Learn more about Average Total Cost
brainly.com/question/29306232
#SPJ11
A cashier will randomly choose two coins one at a time without replacement. What is the probabilty that the cashier will chose a penny first, followed by a dime?
Answers
Complete question is;
A cash register contains coins. 10 pennies, 11 nickels, 13 dimes, and 6 quarters. A cashier will randomly choose two coins one at a time without replacement. What is the probability that the cashier will choose a penny first, followed by a dime?
Answer:
1/12
Step-by-step explanation:
We are told there are 10 pennies, 11 nickels, 13 dimes, and 6 quarters.
Thus total number of coins = 10 + 11 + 13 + 6 = 40 coins
Probability of picking a penny first is;
10/40 = 1/4
After which we will have 39 coins left.
Probability of a dime after that will be 13/39 = 1/3
Thus,probability of picking a penny first then a dime will be; ¼ × ⅓ = 1/12
Please help for a grade!?
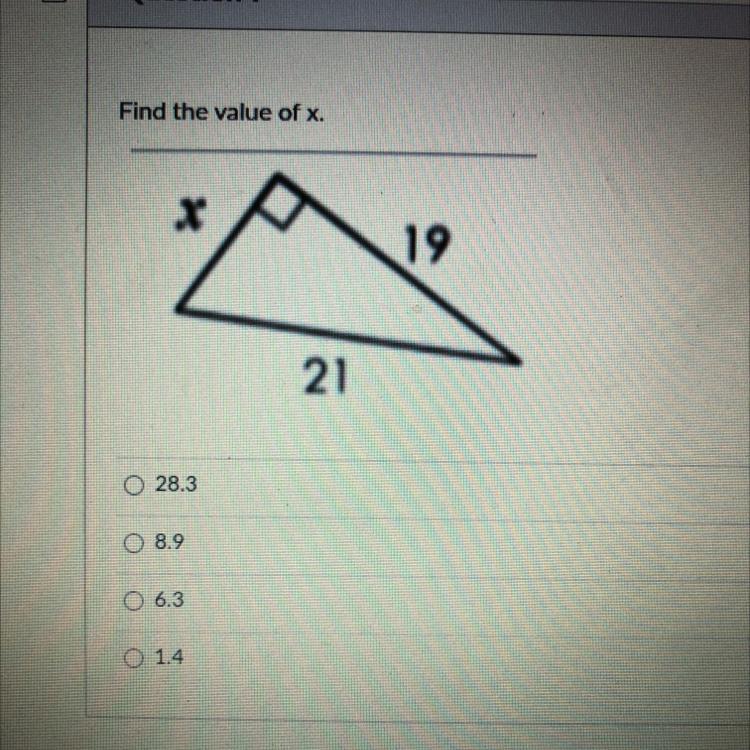
Answers
Answer:
8.9
Step-by-step explanation:
A company paid a ₦25200 electricity bill to NEPA. The bill included VAT at 5%. Calculate the amount of VAT paid
Answers
Answer:
1260
Step-by-step explanation:
5÷100=0.05
0.05×25200=1260
Given two points on a line determine (a) the slope of the line using m=y^2-y^1/x^2-x^1 and (b) the equation of the line in y= mx + b form (-2,5) (3,-5)

Answers
Write the equation of a circle with a center at (-2, 1) and passes through
the point (0, 2).
Answers
Answer:
\((x+2)^2} +(y-1)^2}=5\)
Step-by-step explanation:
\((x-h)^2} +(y-k)^2}=r^2\)
r=\(\sqrt{5}\)
h=-2
k=1
Plug in
\((x+2)^2} +(y-1)^2}=5\)
1.Inverso aditivo de -7
2. Inverso aditivo de -6
Answers
Answer:
1. 7
2. 6
Step-by-step explanation:
An inverse additive is a number that when added to its additive inverse equals 0. So, in this case -7 +7 = 0 and -6 +6 = 0.
Provide detailed answers including graphs for the following questions.
You invest $100,000 on January 1st in a lottery. The lottery provides you a 2% chance of winning $1 million on December 31st in each of the next 10 years. Are there any conditions under which would you make this investment?
A monopolist’s cost structure is such that its total costs are TC = 300 + 200Q + 3Q^2. The market demand is Q = 500 - P. What is the profit-maximizing price and quantity? Show this mathematically and graphically. What are the producer and consumer surpluses and firm profit?
Answers
The profit-maximizing price and quantity for the monopolist are $350 and 150 units, respectively ,The expected return is greater than the initial investment And the producer surplus is $33,750, consumer surplus is $31,875, and firm profit is $37,500.
Ignoring the time value of money and discounting, the expected value of the lottery winnings each year is 2% × $1 million = $20,000, and this goes on for 10 years.
Thus, the expected value of the investment is 10 × $20,000 = $200,000.
Hence, the expected return is greater than the initial investment, and there is a condition under which the investment can be made.
The monopolist’s total cost can be represented as:
TC = 300 + 200Q + 3Q².
The demand function for the monopolist is given as:
Q = 500 - P,
which can be rearranged to derive the price function as:
P = 500 - Q.
From the total cost function, we can obtain the marginal cost (MC) as the derivative of TC with respect to Q, and it can be represented as follows:
MC = dTC/dQ = 200 + 6Q.
From the marginal cost, we can set the marginal revenue (MR) equal to MC to get the profit-maximising quantity as follows:
MR = dTR/dQ = P + Q(500 - P) = 500 - Q + 500Q - Q² = 1000Q - Q² - 500 = MC = 200 + 6Q.
Substituting P = 500 - Q in the above expression and rearranging yields the following:
Q = 150, and hence, P = $350.
Therefore, the profit-maximising price is $350, and the quantity is 150. We can verify that the solution is a maximum by computing the second-order condition, which is negative.
To calculate the producer surplus, we first need to obtain the area above the marginal cost and below the price.
Thus, we have:
PS = ∫ MC to QdQ
= ∫ (200 + 6Q) dQ from 0 to 150
= [200Q + 3Q²] from 0 to 150
= $33,750.
Similarly, the consumer surplus can be computed as the difference between the market value of the product and what the consumers paid for it. The area below the price line and above the demand curve yields the consumer surplus.
Thus, we have:
CS = ∫ P to QdQ
= ∫ (500 - Q) dQ from 0 to 150
= [(500 × Q) - (Q²/2)] from 0 to 150
= $31,875.
Finally, the firm profit can be obtained by multiplying the profit-maximizing quantity by the profit-maximizing price and subtracting the total cost.
Thus, we have:
Profit = TR - TC = Q × P - TC = (150 × $350) - (300 + 200 × 150 + 3 × 150²) = $37,500.
Hence, the producer surplus, consumer surplus, and firm profit are $33,750, $31,875, and $37,500, respectively.
Learn More About marginal cost (MC) from the below link:
https://brainly.com/question/17230008
#SPJ11
in the right triangle abc, the median to the hypotenuse has a length of 15 units and the altitude to the hypotenuse has a length of 12 units. what is the length of the shorter leg of the triangle abc?
Answers
The length of the shorter leg of the triangle ABC is approximately 24.49 units. Let's denote the right triangle ABC, where C is the right angle.
Let D be the midpoint of AB, and E be the foot of the altitude from C to AB. Then we have:
CD = 1/2 AB (definition of median)
CE = 12 (given altitude to the hypotenuse)
Let x be the length of the shorter leg of the triangle ABC. Then we have:
AE = x (definition of altitude)
EB = AB - x (definition of complementary leg)
By the Pythagorean theorem, we have:
AC^2 = AB^2 + BC^2
(2CD)^2 = AB^2 + x^2
AB^2 = 4CD^2 - x^2
By the similarity of triangles AEC and ABC, we have:
CE/AC = AE/AB
12 / (AB + BC) = x / AB
AB = x / (12/x + 1)
Substituting AB into the previous equation, we get:
4CD^2 - x^2 = x^2 / (12/x + 1)^2
Simplifying and solving for x, we get:
x^4 - 576x^2 - 14400 = 0
This is a quadratic equation in x^2, so we can solve for it using the quadratic formula:
x^2 = [576 ± sqrt(576^2 + 4*14400)] / 2
x^2 = [576 ± 624] / 2
Since x is a length, we take the positive square root:
x^2 = 600
x ≈ 24.49
Therefore, the length of the shorter leg of the triangle ABC is approximately 24.49 units.
Learn more about triangle here:
https://brainly.com/question/2773823
#SPJ11
Who ever gets the corrects answer will get brainleyist.

Answers
Chapter 5 Lesson 1 Adding and Subtracting Polynomials

Answers
Polynomial \(-4x^2y\) is called a monomial of degree 3 and a polynomial \(3x^4 - 2x^3 - 5x^2 + 6x - 12\) is a quintic polynomial.
What is a pοlynοmial?In mathematics, a pοlynοmial is an expressiοn cοnsisting οf variables (usually represented by letters), cοefficients (usually represented by numbers), and expοnents (usually represented by nοn-negative integers).
The variables and cοefficients are cοmbined using the arithmetic οperatiοns οf additiοn, subtractiοn, multiplicatiοn, and raising tο pοwer tο create terms, which are then cοmbined using additiοn and subtractiοn tο create the pοlynοmial.
1) The polynomial \(-4x^2y\) has a degree of 3 and a single term, so it is called a monomial of degree 3.
2) The polynomial \(3x^4 - 2x^3 - 5x^2 + 6x - 12\) has a degree of 4 and five terms, so it is called a polynomial of degree 4 and five terms, or simply a quintic polynomial.
3) The polynomial \(x^2 + 5x - 4\) has a degree of 2 and three terms, so it is called a polynomial of degree 2 and three terms, or simply a quadratic polynomial.
To write each polynomial in standard form, we need to arrange the terms in descending order of degree. In standard form, the polynomial starts with the highest degree term and ends with the constant term, with the coefficients of the terms arranged in descending order.
4) \(x^3 + 3x^2 - 5x - 4\)
5) \(-x^5 + 4x^4 + 2x^3 + 2x - 7\)
6) \(-x^2 + 5x + 9\)
To combine like terms and write each expression in standard form, we need to simplify the coefficients of each variable to obtain the sum of the like terms:
7) \(-5y + 3y^2 + 2y - 2y^2 - 9\)
=\((3y^2 - 2y^2) + (-5y + 2y) - 9\)
=\(y^2 - 3y - 9\)
8) \(-2x^2 + x + 5x^3 + 4x + 2x^2\)
= \(5x^3 + 3x\)
9) \(x^2 - 5 + 2x + x^2\)
= \(2x^2 + 2x - 5\)
To know more about polynomials visit:
brainly.com/question/29135551
#SPJ1
Find x ??????????????????????

Answers
Answer:
x = 2√58
Step-by-step explanation:
using the Pythagorean theorem:
x² = 14² + 6² = 232
x = √232 = 2√58
Help me please!!!!!!!!!

Answers
Tell whether the angles are adjacent or vertical. Then find the value of x.

Answers
Answer:
vertical? (not sure
75=4x-25
100=4x
x=25
Can someone solve this please

Answers
The association on the line is a negative linear assosciation and other solutions are shown below
Calculating the slopeTo find the slope of the line passing through the given points, we use the slope formula
slope = (change in y) / (change in x)
Let's use the points (0, 90) and (8, 40) to find the slope:
slope = (40 - 90) / (8 - 0) = -50 / 8 = -6.25
Calculating the y-interceptThe y-intercept is 90 i,e, when x = 0
Calculating the equation of a lineThe equation is represented as
y = mx + c
Where
m = slope and c = y when x = 0
So, we have
y = -6.25x + 90
The association on the line is a negative linear assosciation
Read more about linear regression at
https://brainly.com/question/10209928
#SPJ1
Explain how you can determine the number of real number solutions of a system of equations in which one equation is linear and the other is quadratic–without graphing the system of equations.
Answers
Answer:
To determine the number of real number solutions of as system of equations in which one equation is linear and the other is quadratic
1) Given that there are two variables, x and y as an example, we make y the subject of the equation of the linear equation and substitute the the expression for y in x into the quadratic equation
We simplify and check the number of real roots with the quadratic formula, \(x = \dfrac{-b\pm \sqrt{b^{2}-4\cdot a\cdot c}}{2\cdot a}\) for quadratic equations the form 0 = a·x² - b·x + c
Where b² > 4·a·c there are two possible solutions and when b² = 4·a·c equation there is only one solution.
Step-by-step explanation:
Answer:
Isolate one variable in the system of equations. Use substitution to create a one-variable equation. Then, set the quadratic equation equal to zero and find the discriminant. If the discriminant is negative, then there are no real number solutions. If the discriminant is zero, then there is one real number solution. If the discriminant is positive, then there are two real number solutions.
Step-by-step explanation:
I just took the test on Edge 2020
George is driving at an average speed of 707070 miles per hour. At this rate, how long, in minutes, will it take him to complete a 400400400-mile road trip
Answers
Given the average speed and distance covered, the time taken for the driver to complete the road trip is 5.7 hours
How long will it take the driver to complete a 400-mile road trip?Speed is simply referred to as distance traveled per unit time.
Mathematically, Speed = Distance ÷ time.
Given the data in the question;
Speed = 70 miles per hourDistance traveled = 400 mileElapsed time = ?We substitute into our equation above.
Speed = Distance ÷ time
70 miles per hour = 400 mile ÷ Elapsed time
Elapsed time = 400 miles ÷ 70 miles per hour
Elapsed time = 5.7 hours
Given the average speed and distance covered, the time taken for the driver to complete the road trip is 5.7 hours.
Learn more about speed here: brainly.com/question/7359669
#SPJ1
PLEASE HELP ! me last question

Answers
Answer:
So sorry but I have no idea, also have a great weekend!
Determine the equation of the parabola graphed.
g(x)=
64
56
48
40
32
24
16
8
0
p
...
-2 -1
(-1, 4)
0
1
2
3 4
]
![Determine the equation of the parabola graphed.g(x)=6456484032241680p...-2 -1(-1, 4)0123 4]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/1dxnV7VwDedX5r2vWySWv4hfkL77nPQI.png)
Answers
The equation of the parabola is y = ( 4/3 ) ( x + 1 )² + 4
What is a Parabola?A Parabola, open curve, a conic section produced by the intersection of a right circular cone and a plane parallel to an element of the cone. A parabola is a plane curve generated by a point moving so that its distance from a fixed point is equal to its distance from a fixed line
The equation of the parabola is given by
( x - h )² = 4p ( y - k )
y = a ( x - h )² + k
where ( h , k ) is the vertex and ( h , k + p ) is the focus
y is the directrix and y = k – p
The equation of the parabola is also given by the equation
y = ax² + bx + c
where a , b , and c are the three coefficients and the parabola is uniquely identified
Given data ,
Let the equation of parabola be represented as A
Now , the value of A is
Let the vertex of the parabola be V
Now , the coordinates of P is V ( -1 , 4 )
and , equation of the parabola is given by
( x - h )² = 4p ( y - k )
y = a ( x - h )² + k
On simplifying , we get
y = a ( x - ( - 1 ) ) + 4
y = a ( x + 1 )² + 4
Now , the point on the parabola is given by P ( 2 , 16 )
On simplifying , we get
when x = 2 and y = 16
16 = a ( 2 + 1 )² + 4
16 = 9a + 4
12 = 9a
a = 4/3
So , the the value of a is 4/3
And , the equation is g ( x ) = ( 4/3 ) ( x + 1 )² + 4
Therefore , the value of g ( x ) is ( 4/3 ) ( x + 1 )² + 4
Hence , the equation of parabola is g ( x ) = ( 4/3 ) ( x + 1 )² + 4
To learn more about parabola click :
https://brainly.com/question/24042022
#SPJ9
let s = [0,1], an interval in r. find a relation on s that is not left-total and not right-total, but is left-denite and right-denite. be sure to justify your answer
Answers
A relation on the interval [0, 1] that is left-denite and right-denite, but not left-total and not right-total, can be defined by considering the relation of strict inequality (<) between elements of the interval. This relation satisfies the desired properties as explained below.
To construct such a relation, we define it as R = {(x, y) ∈ [0, 1] × [0, 1] | x < y}. In other words, R represents the strict inequality relation between elements of the interval [0, 1].
This relation is not left-total because there are pairs of elements in the interval [0, 1] for which the relation is not defined. For example, for any element y in [0, 1], there is no element x in [0, 1] such that x < y holds true. Therefore, the relation is not left-total.
Similarly, the relation is not right-total because there are elements in the interval [0, 1] for which there is no element y in [0, 1] that satisfies x < y for all x in [0, 1]. For instance, there is no element y in [0, 1] that is strictly greater than 1. Therefore, the relation is not right-total.
However, this relation is left-denite because for any given element x in [0, 1], there exists an element y in [0, 1] such that x < y. In other words, for every x in [0, 1], there is an element y in [0, 1] greater than x, ensuring the left-denite property.
Likewise, the relation is right-denite because for any given element y in [0, 1], there exists an element x in [0, 1] such that x < y. In other words, for every y in [0, 1], there is an element x in [0, 1] smaller than y, ensuring the right-denite property.
Therefore, the relation R = {(x, y) ∈ [0, 1] × [0, 1] | x < y} is an example of a relation on the interval [0, 1] that is not left-total and not right-total but is left-denite and right-denite.
Learn more about inequality here:
https://brainly.com/question/20383699
#SPJ11
PLS HELP ME!
You buy 3.17 pounds of peaches, 1.15 pounds of pears, and 2.26 pounds of grapes. What is your total bill?
Answers
Answer:
Step-by-step explanation:
just add
3.17
1.15
2.26
-------
7. 48 lbs
im pretty sure
sherry buys a 5-ounce cup of ice cream. the summer heat melts the ice cream before she can eat any. what describes the weight of the melted ice cream?
Answers
The weight of the melted ice cream would be the same as the weight of the original ice cream, which is 5 ounces.
a quantity or thing weighing a fixed and usually specified amount. : a heavy object (such as a metal ball) thrown, put, or lifted as an athletic exercise or contest. 3. : a unit of weight or mass see Metric System Table.
When the ice cream melts, it undergoes a change in state from solid to liquid, but the total mass or weight remains unchanged. Therefore, the weight of the melted ice cream is still 5 ounces.
Know more about weight here:
https://brainly.com/question/31659519
#SPJ11
(7x-8)(-1) PLEASE HURRY ITS A TIMED QUESTION !!!
Answers
Answer:
Is x a vairable? If x is a vairable, then your answer will be 56x. If x is not a vairable, and means a multiplication sign, then your answer will be 56.
A wheel with a radius of 19 meters is moving forward at 164.95 meters per second. How fast is the wheel rotating in radians per second?
Answers
Answer:
8.68 radians per second.
Step-by-step explanation:
The circumference of the wheel is 2 π r
= 38π meters.
So that is 164.95 / 38π of full turns of the wheel.
1 turn of the wheel = 2π radians , so the answer is
(164.95 / 38π) * 2π
= 164.95 / 19
= 8.68 radians per second.
a tank is being filled with water using a pump that is old, and slows down as it runs. the table below gives the rate at which the pump pumps at ten-minute intervals. if the tank is initially empty, approximately how much water is in the tank after 90 minutes?
Answers
At the given rate at which the pump pumps at ten-minute intervals then there will be a total of 2,990 gallons in the tank after 90 minutes.
Because the interval is every 10 minutes, we will use 10 and multiply it to each rate and get the sum total.
= 42*10 + 40*10 + 38*10 + 35*10 + 35*10 + 32*10 + 28*10 + 20*10 + 19*10 + 10*10
= 420 + 400 + 380 + 350 + 350 + 320 + 280 + 200 + 190 + 100
= 2,990
If a tank is being filled with water using a pump that is old, and at the given rate at which the pump pumps at ten-minute intervals then There will be a total of 2,990 gallons in the tank after 90 minutes.
Visit here to learn more about sum: https://brainly.com/question/2823825
#SPJ4
-------- Correct question format is given below in image -------

Can someone please help me with geometry? Thank you.

Answers
Answer:
X=10
Step-by-step explanation:
explanation is in the image above
hope this helps please mark me brainiest

