Hey!! Can you guys help me !!
No links!!
No spams!!
Ahmed paid $34 000 for a car. His car decreased in value by 40% at the end of the first year. The value at the end of the second year was 10% less than the value at the end of the first year. . Calculate the value of Ahmed's car after 2 years .
Answers
40% of 34 000
40/100 * 34 000 = 13 600
subtract : 34000 - 13 600 = 20 400
Second step:10% of 20 400
10/100 * 20 400 = 2040
subtract : 20 400 - 2040 = $ 18 360
Final Answer = $ 18 360Related Questions
URGENT! Will earn 100 points if you can answer all of these questions on PAPER OR DOCUMENT. Send link to email, messages, or through the answer page.
( MESSAGE JamSandwitch FOR EMAIL AND TO SEND DOCUMENT / ANSWERS ! )


Answers
Answer:
see below
Step-by-step explanation:
3) 8
4) 4
5) 14
6) 47
7) 18/5
8) 3/2
9) 255/4
10) 16
11) 21
12) 40
13) 73.5
14) 1
15) 25/2 or 12.5
16) 0
17) 48
18) 862
19) 9765625
20) 343
21) 8.1x10⁻³
22) 10.24
23) 1/156
24) n⁷
25) y⁶
26) t⁴
27) error is 0.4² should be 0.02²
28) 5⁴ = 5 x 5 x 5 x 5 = 625
29) 9
30) 100
31) 1
32) 1331
33) 125
34) 1024
35) 64
36) 1296
37) 1/16
38) 16/81
39) 27/125
40) 1/216
hope you enjoy the answers.
Answer:
thx
Step-by-step explanation:
When cooper was 15 years old, he scored an 85 on an iq test. he took the test again when he was 35 years old and scored an 85 again. this indicates that the iq test is highly: __________
Answers
Answer:
When cooper was 15 years old, he scored an 85 on an iq test. he took the test again when he was 35 years old and scored an 85 again. this indicates that the iq test is highly: __________
Reliable
Because his scores were so close together the test would be considered as Reliable.
Know more about “intelligent iq question” here: https://brainly.com/question/28319133
#SPJ4
question is in the picture

Answers
Answer:
4th triangle
Step-by-step explanation:
The correct answer for the given problem above would be the fourth triangle. So here is the given solution: Since Triangle 1 is already given with a measurement of 50 inches, and 80% of 50 inches if 40. Triangle 2 then is 40 inches. 80% of 40 is 32, so triangle 3 is 32 inches, and then 80% of 32 is 25.6 inches so triangle 4 is 25.6 inches. Therefore, the triangle that will first have a side length of less than 29 inches is triangle 4.
hope this was helpful :)
Write 4.5 as a mixed number and as an improper fraction
Write your answer in a simplest form m
Answers
9/2 improper fraction
Answer:
4.5 as a mixed number is 4 1/2
4.5 as an improper fraction is 9/2
Solve the equation by factoring.
x² + 2x - 63 = 0
x = -9, [?]
Answers
Step-by-step explanation:
x² + 2x - 63 = 0
(x+9)(x-7)=0
x=-9 x=7
we are told that 7% of college graduates, under the age of 20 are unemployed. what is the probability that at least 200 out of 210 college graduates under age 20 are employed?
Answers
P(X ≥ 200) = 1 - P(X < 200) ≈ 1.0. In other words, it is very likely (almost certain) that at least 200 out of 210 college graduates under age 20 are employed.
To find the probability that at least 200 out of 210 college graduates under age 20 are employed, we can use the binomial distribution formula:
P(X ≥ 200) = 1 - P(X < 200)
where X is the number of employed college graduates under age 20 out of a sample of 210.
We know that the unemployment rate for college graduates under the age of 20 is 7%. Therefore, the probability of an individual college graduate being unemployed is 0.07.
To find the probability of X employed college graduates out of 210, we can use the binomial distribution formula:
P(X = k) = (n choose k) * p^k * (1-p)^(n-k)
where n is the sample size (210), k is the number of employed college graduates, and p is the probability of an individual college graduate being employed (1-0.07=0.93).
We want to find P(X < 200), which is the same as finding P(X ≤ 199). We can use the cumulative binomial distribution function on a calculator or software to find this probability:
P(X ≤ 199) = 0.000000000000000000000000000001004 (very small)
Therefore, P(X ≥ 200) = 1 - P(X < 200) ≈ 1.0. In other words, it is very likely (almost certain) that at least 200 out of 210 college graduates under age 20 are employed.
To know more about probability visit:
https://brainly.com/question/31120123
#SPJ11
A ball i drawn randomly from a jar that contain 5 red ball, 2 white ball, and 1 yellow ball. Find the probability of: Find P(red ball): Find P(NOT Yellow): Find P(white or yellow)
Answers
Following are all of the subparts' solutions using the probability formula:
Red ball (A) P: 5/8
(B) P: 7/8 (NOT Yellow)
(C) P(yellow or white): 3/8
What is probability?
Probability is a branch of mathematics that deals with numerical representations of the likelihood of an event occurring or of a proposition being true.
What is an event?The probability of an event is a number between 0 and 1, with 0 approximately denoting impossibility and 1 denoting certainty.
Probability formula: P(E) = favorable events/Total events
(A) P(red ball):
P(E) = favorable events/Total events
P(E) = 5/8
(B) P(NOT Yellow)
P(E) = favorable events/Total events
P(E) = 7/8
(C) P(white or yellow)
P(E) = favorable events/Total events
P(E) = 3/8
Therefore, the answers to all the subparts using the probability formula are shown:
(A) P(red ball): 5/8
(B) P(NOT Yellow): 7/8
(C) P(white or yellow): 3/8
To Know more about probability visit:
https://brainly.com/question/11234923
#SPJ4
A road perpendicular to a highway leads to a farmhouse located 2 km away. A car travels pastthe farmhouse on on the highway at a speed of 80 km/h. How fast is the distance between thecar and the farmhouse increasing when the car is 6 km past the intersection of the highwayand the road
Answers
Answer:
75.9 km/hr
Step-by-step explanation:
Distance between the highway and farmhouse is given as = 2km = a
The distance after the intersection and the highway = b
Let the distance between the farmhouse and the car = c
Using the Pythagoras Theorem rule
c² = a² + b²
c² = 2² + b²
Step 1
Since distance is involved, time is required. Hence, we differentiate the equation above in respect to time
c² = 2² + b²
dc/dt (2c) = 4 + 2b
dc/dt =[ b/(√b² + 4)] × db/dt
We are told in the question that:
the car travels past the farmhouse on on the highway at a speed of 80 km/h.
We are asked to calculate the speed at which the distance between the car and the farmhouse kept increasing when the car is 6 km past the intersection of the highway and the road.
This calculated using the obtained differentiation above:
dc/dt = [ b/(√b² + 4)] × db/dt
Where b = 6km
db/dt = 80km/hr
[6/(√6² + 4)] × 80km/hr
6/√36 + 4 × 80km/hr
6 × 80/√40
480/√40
= 75.894663844km/hr
Approximately = 75.9km/hr
In this exercise we want to calculate the speed of the vehicle to reach the farm, in this way we will find a speed of approximately:
\(75.9 km/hr\)
To start this exercise we have to use some data informed in the text, like this:
Distance: \(a=2km\) Distance after the intersection and the highway: \(b\) Distance between the farmhouse and the car: \(c\) Pythagoras Theorem rule: \(c^2 = a^2 + b^2\)
Since distance is involved, time is required. Hence, we differentiate the equation above in respect to time
\(c^2 = 2^2 + b^2\\\frac{dc}{dt} (2c) = 4 + 2b\\\frac{dc}{dt} =[ b/(\sqrt{b^2} + 4)] ( \frac{db}{dt})\)
Calculate the speed at which the distance between the car and the farmhouse kept increasing when the car is 6 km past the intersection of the highway and the road. This calculated using the obtained differentiation above:
\(\frac{dc}{dt} = [ 6/(\sqrt{6^2} + 4)] (80)\\=6/\sqrt{36} + 4 * 80\\=6 * 80/\sqrt{40} \\=480/\sqrt{40} \\= 75.9km/hr\)
See more about speed at brainly.com/question/312131
Is the trapezoidal rule an overestimate or underestimate?
Answers
The trapezoidal rule is a numerical integration method that frequently overestimates the real value of a function's definite integral.
What is trapezoidal rule?The trapezoidal rule is a strategy for approximating the definite integral in calculus. The trapezoidal rule works by computing the area of the region under the graph of the function f(x) that is approximated as a trapezoid. The trapezoidal rule is commonly used to calculate the area under curves. This is achievable if the overall area is divided into smaller trapezoids rather than rectangles. The Trapezoidal Rule integration determines the area by approximating the area under a function's graph as a trapezoid. The midway rule uses rectangular areas to approximate the definite integral, whereas the trapezoidal rule uses trapezoidal approximations to approximate the definite integral. Simpson's approach works by first approximating the original function with piecewise quadratic functions.
To know more about trapezoidal rule,
https://brainly.com/question/17218343
#SPJ4
I’m not sure how to answer?

Answers
The transformation of the graph f(x) = x² to the graph g(x) = -3(x+5)² + 12 involves a horizontal shift, a vertical stretch, and a vertical translation.
The graphs of f(x) = x² and g(x) = -3(x+5)² + 12 are the parabola.
The transformation of the graph is following as:
Firstly, the parabola has been shifted horizontally by 5 units to the left, which is reflected in the expression (x+5)².
Secondly, the parabola has been stretched vertically by a factor of -3, which is reflected in the coefficient in front of (x+5)².
Finally, the parabola has been raised up to 12 units. This means that the vertex of the parabola has been shifted upwards from the origin to the point (−5,12).
Learn more about the transformation here:
https://brainly.com/question/28772799
#SPJ1
Which statement correctly compares the areas of these two rectangles?

Answers
A statement that correctly compares the areas of these two rectangles is that the area of the yellow rectangle is greater than the area of the blue rectangle by 8 square units.
How to calculate the area of a rectangle?In Mathematics and Geometry, the area of a rectangle can be calculated by using the following mathematical equation:
A = LW
Where:
A represent the area of a rectangle.W represent the width of a rectangle.L represent the length of a rectangle.Based on the information provided about these rectangles, we have the following:
Area of blue rectangle = 10 × 4
Area of blue rectangle = 40 square units.
Area of yellow rectangle = 6 × 8
Area of yellow rectangle = 48 square units.
Difference = Area of yellow rectangle - Area of blue rectangle
Difference = 48 - 40
Difference = 8 square units.
Read more on area of a rectangle here: brainly.com/question/29604954
#SPJ1
Another thrifty student has saved up $1400 working at City Beach. This person put the money into an account for
1 year, which generated $70 interest. What was the interest rate?
how do i work out the interest rate?
Answers
Answer 20%
Step-by-step explanation:
Let p be the statement "There are four seasons" and let q be the statement "It was composed by Vivaldi." What statement is represented by the symbolic form p∧q?Select the correct answer below:There are four seasons or it was composed by Vivaldi.There are not four seasons or it was composed by Vivaldi.There are four seasons or it wasn't composed by Vivaldi.There are four seasons and it was composed by Vivaldi.
Answers
Solution:
Given;
p: There are four seasons.
q: It was composed by Vivaldi.
\(\wedge\text{ means }and\)Thus;
\(p\wedge q\)ANSWER: There are four seasons and it was composed by Vivaldi.
Calculate the pore compressibility Cpp with porosity 0 = 0.2, Young modulus E = 10 GPa, Poisson's ratio v = 0.2. =
Answers
The pore compressibility (Cpp) can be calculated using the given parameters: porosity (0), Young's modulus (E), and Poisson's ratio (v). With a porosity of 0.2, Young's modulus of 10 GPa, and Poisson's ratio of 0.2, we can determine the pore compressibility.
Pore compressibility is a measure of how much a porous material, such as soil or rock, compresses under the application of pressure. It quantifies the change in pore volume with respect to changes in pressure.
Cpp = (1 - φ) / (E * (1 - 2ν))
Given the values:
φ = 0.2 (porosity)
E = 10 GPa (Young's modulus)
ν = 0.2 (Poisson's ratio)
Substituting these values into the formula, we have:
Cpp = (1 - 0.2) / (10 GPa * (1 - 2 * 0.2))
Simplifying the equation, we get:
Cpp = 0.8 / (10 GPa * (1 - 0.4))
= 0.8 / (10 GPa * 0.6)
= 0.8 / 6 GPa
= 0.133 GPa^(-1)
Therefore, the pore compressibility (Cpp) is approximately 0.133 GPa^(-1).
Learn more about Poisson's ratio here:
https://brainly.com/question/31967309
#SPJ11
Explain how to plot the point (3, –7) on the coordinate plane.On a coordinate plane, point A is (negative 4, negative 1), point B is (negative 4, 1), point C is (5, negative 1), and point D is (5, 2). Point P is at (5, 1). Which point is a reflection of Point P across the x-axis?
Answers
Answer:
a) In a coordinate plane, the horizontal axis is the x-axis, and the vertical axis is the y-axis.
So, a point (x, y) is at:
A horizontal distance of x units from the origin.
A vertical distance of y units from the origin.
So the point (3, -7) is at:
3 units at the right from the origin
7 units downwards (because is a -7) from the origin.
The graph of the point can be seen below:
Now we want to find a reflection across the x-axis.
b) For a general point (x, y), a reflection across the x-axis gives:
(x, -y)
So, if our point P is:
P (5, 1)
The reflection across the x-axis just changes the sign of the y-value, which gives:
(5, -1)
Then the correct option is point C:
(5, -1)

Answer:
its C on exgenity
Step-by-step explanation:
PLEASE HELP Me!!!!!!!!!!

Answers
Answer:84
Step-by-step explanation:
hope this helps :))
Bellwork: open a word document and type the following:
What are the 5 forms of energy?
Give an example of each to discuss in class in a few minutes.
Agenda: day 2 notes on alternate energy
Assignment chose one of the 2 to complete
Posted nov 16 by Jolene McCall

what is the percent of change from 25 to 29
Answers
well, clearly is 4 :).
now, if we take 25 to be the 100%, what is 4 off of it in percentage?
\(\begin{array}{ccll} amount&\%\\ \cline{1-2} 25 & 100\\ 4& x \end{array} \implies \cfrac{25}{4}~~=~~\cfrac{100}{x} \implies 25x=400\implies x=\cfrac{400}{25}\implies x=16\)
The table shown below provides statistical data on the bowling scores for David and Elise.
David claims that his scores were more consistent than Elise’s scores. Which statement is MOST likely true about David’s claim?
David’s claim is correct because his mean score is greater than Elise’s mean score.
David’s claim is correct because the interquartile range for his scores is greater than the interquartile range for Elise’s scores.
check
David’s claim is incorrect because his mean score is greater than Elise’s mean score.
David’s claim is incorrect because the interquartile range for his scores is greater than the interquartile range for Elise’s scores.

Answers
The correct statement regarding David's claim is given as follows:
David’s claim is incorrect because the interquartile range for his scores is greater than the interquartile range for Elise’s scores.
How to obtain the interquartile range?The interquartile range of a data-set is given by the difference of the third quartile by the first quartile of the data-set.
The interquartile range is a metric of consistency, and the lower the interquartile range, the more consistent the data-set is.
The interquartile range for David is greater than for Elise, hence his claim is incorrect.
More can be learned about the interquartile range at brainly.com/question/12323764
#SPJ1
Use the definition of Taylor series to find the Taylor series (centered at c ) for the function. f(x)=e 4x
,c=0 f(x)=∑ n=0
[infinity]
Answers
The answer is , the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
The Taylor series expansion is a way to represent a function as an infinite sum of terms that depend on the function's derivatives.
The Taylor series of a function f(x) centered at c is given by the formula:
\(\large f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(c)}{n!}(x-c)^n\)
Using the definition of Taylor series to find the Taylor series (centered at c=0) for the function f(x) = e^(4x), we have:
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{e^{4(0)}}{n!}(x-0)^n\)
\(\large e^{4x} = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n\)
Therefore, the Taylor series (centered at c=0) for the function f(x) = e^(4x) is given by:
\($$\large f(x) = \sum_{n=0}^{\infty} \frac{4^n}{n!}x^n$$\)
To know more about Function visit:
https://brainly.in/question/222093
#SPJ11
The Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To find the Taylor series for the function f(x) = e^(4x) centered at c = 0, we can use the definition of the Taylor series. The general formula for the Taylor series expansion of a function f(x) centered at c is given by:
f(x) = f(c) + f'(c)(x - c) + f''(c)(x - c)^2/2! + f'''(c)(x - c)^3/3! + ...
First, let's find the derivatives of f(x) = e^(4x):
f'(x) = d/dx(e^(4x)) = 4e^(4x)
f''(x) = d^2/dx^2(e^(4x)) = 16e^(4x)
f'''(x) = d^3/dx^3(e^(4x)) = 64e^(4x)
Now, let's evaluate these derivatives at x = c = 0:
f(0) = e^(4*0) = e^0 = 1
f'(0) = 4e^(4*0) = 4e^0 = 4
f''(0) = 16e^(4*0) = 16e^0 = 16
f'''(0) = 64e^(4*0) = 64e^0 = 64
Now we can write the Taylor series expansion:
f(x) = f(0) + f'(0)(x - 0) + f''(0)(x - 0)^2/2! + f'''(0)(x - 0)^3/3! + ...
Substituting the values we found:
f(x) = 1 + 4x + 16x^2/2! + 64x^3/3! + ...
Simplifying the terms:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
Therefore, the Taylor series for f(x) = e^(4x) centered at c = 0 is:
f(x) = 1 + 4x + 8x^2 + 32x^3/3 + ...
To know more about Taylor series, visit:
https://brainly.com/question/32235538
#SPJ11
In triangle ABC, m ZA = 47°, m ZB = 62°. m ZC =
a. 81°
b. 61°
C. 71
d. 51°
Answers
Answer:
m ZC = 71 degrees. Option C.
Step-by-step explanation:
Triangles always measure a total of 180 degrees.
47 + 62 + c = 180
109 + c = 180
c = 71
Answer:
71°
Step-by-step explanation:
The total angles in a triangle should equal 180°
a + b + c = 180
47 + 62 + c = 180
109 + c = 180
180 - 109 = 71
c = 71°
Hope this helped!
A useful and easy-to-remember approximate value for the number of seconds in a year is p * 107. Determine the percent error in this approximate value. (there are 365.24 days in one year.)
Answers
The percent error in the approximate value for the number of seconds in a year (p * 107) can be determined by comparing it to the actual value, which is calculated as 31,556,864 seconds. The percent error can be found using the formula [(Approximate Value - Actual Value) / Actual Value] * 100.
To determine the percent error in the approximate value for the number of seconds in a year (p * 107), we need to compare it to the actual value. The actual value can be calculated by multiplying the number of seconds in a day (24 hours * 60 minutes * 60 seconds) by the number of days in a year (365.24).
Actual value = (24 * 60 * 60) * 365.24 = 31,556,864 seconds
Now, let's calculate the percent error using the formula:
Percent Error = [(Approximate Value - Actual Value) / Actual Value] * 100
Approximate Value = p * 107
Actual Value = 31,556,864
Percent Error = [(p * 107 - 31,556,864) / 31,556,864] * 100
Since we don't have the value of p, we cannot determine the exact percent error. However, we can still express it in a general form using the given terms.
The percent error in the approximate value for the number of seconds in a year (p * 107) can be determined by comparing it to the actual value, which is calculated as 31,556,864 seconds. The percent error can be found using the formula [(Approximate Value - Actual Value) / Actual Value] * 100.
To know more about percent visit:
https://brainly.com/question/31323953
#SPJ11
is this triangle congruent?
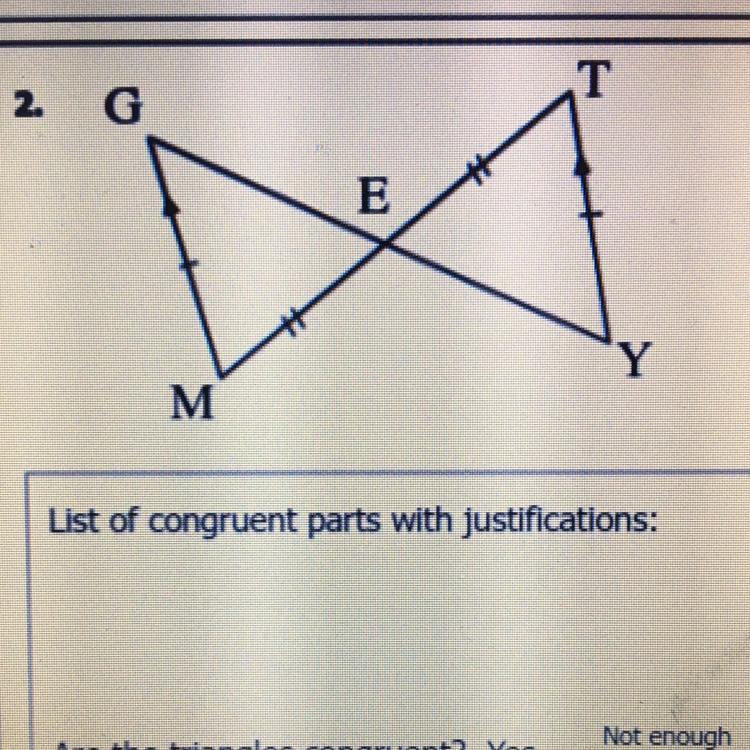
Answers
The distance between -7 and 2 on the number Iine is
O 10
09
0-5
05
Answers
Answer:
9
Step-by-step explanation:
Calculate the absolute difference of the 2 points, that is
| - 7 - 2 | = | - 9 | = 9 , or
| 2 - (- 7) | = | 2 + 7 | = | 9 | = 9
Answer:
9
Step-by-step explanation:
You count Down from -7
ex -7,-6,-5
until you get to zero. While doing this the member the amount of times that you counted a number. You should have counted 7. Then you add 2. You could also add 7 and 2 right away.
(Note, if you add 7 and 2 right away, makes sure 7 is a positive number.)
HELPPPPP MEE ITS DUE TODAY pleasseee

Answers
Please help it's a math problem, I need this due in a few minutes

Answers
Answer:
Proportional
Step-by-step explanation:
Search up the definition of proportional.
Answer:
proportional
Step-by-step explanation:
f(x)=5x-4
Thanks for your help in advance!

Answers
Answer:
x value 0 yields y value of -4
x value 1 yields y value of 1
x value 2 yield y value of 6
Step-by-step explanation:
All we have to do to solve this question is plug in the value of x into the function and get the output or y.
When we plug in 0 we get 5(0)-4. 0 times any number is 0 so the first answer is 0.
When we plug in 1 we get 5(1)-4. This is just 5-4 or 1.
When we plug in 2 we get 5(2)-4. This is just 10-4 or 6.
I hope you liked my answer. Thanks
Which linear equation shows a proportional relationship? a. y equals two thirds times x
b. y equals negative 3 times x minus one seventh c. y equals three fourths times x minus 5 d. y equals 3 times x plus 7
Answers
Answer:
Option a represents a proportional relationship.
Step-by-step explanation:
A proportional relationship is a relationship where two variables are directly related to one another, meaning that their ratio is always the same. In other words, when one variable changes, the other variable also changes in the same ratio.
In the equation y = 2/3 * x, the value of y is directly proportional to the value of x, meaning that for every change in x, the corresponding change in y will always be 2/3 of that change. This is because the coefficient of x is a constant value, in this case 2/3. Therefore, as x increases or decreases, y will also increase or decrease at the same rate in proportion to x.
Option a represents a direct proportion.
Option b, c, and d are not proportional relationships because they include a constant or an operation like subtraction, addition or negative sign.
Read more about proportional relationships:
https://brainly.com/question/29765554
#SPJ4
A company finds 5 defective toys in a sample of 600. Predict how many defective toys are in a
shipment of 24,000.
Answers
Answer:
x = 200Step-by-step explanation:
A company finds 5 defective toys in a sample of 600. Predict how many defective toys are in a
shipment of 24,000.
we can solve with an equation
5 : 600 = x : 24000
x = 5 * 24000 : 600
x = 200
at a certain gas station, 35% of the customers use regular unleaded gas, 35% use extra unleaded gas, and the remainder use premium unleaded gas. of those using regular gas, only 50% fill their tanks. of those customers using extra unleaded, 30% fill their tanks, whereas of those using premium unleaded, 30% fill their tanks. if the next customer fills the tank, what is the probability that extra unleaded gas was requested? (give your answer in percentage terms with one decimal point of precision.)
Answers
The probability that extra unleaded gas was requested is 35%.
To find the probability that the next customer requested extra unleaded gas, we need to first find the total probability that any customer requests extra unleaded gas.
Since 35% of customers request extra unleaded gas, the probability that a customer requests it is 35%. Of those customers, 30% fill their tanks, so the probability that a customer requesting extra unleaded gas fills their tank is 30%.
Therefore, the probability that a customer requesting extra unleaded gas fills their tank is (35%) * (30%) = 0.105, or about 10.5%.
This is the probability that the next customer requested extra unleaded gas and fills their tank. To find the probability that the next customer simply requested extra unleaded gas, regardless of whether they fill their tank or not, we need to add the probabilities of them requesting extra unleaded gas and either filling or not filling their tank.
The probability that the next customer requested extra unleaded gas and filled their tank is 0.105, as we calculated above. The probability that the next customer requested extra unleaded gas and did not fill their tank is (35%) * (70%) = 0.245, or about 24.5%.
To find the total probability that the next customer requested extra unleaded gas, we need to add these two probabilities: 0.105 + 0.245 = 0.35, or 35%. This is the probability that the next customer requested extra unleaded gas.
To learn more about probability,
visit; brainly.com/question/29381779
#SPJ4
What is the slope of the line shown?
On a coordinate plane, a line goes through (0, negative 3) and (6, 0).
Answers
Answer:
1/2
Step-by-step explanation: